Курсовой ОТЦ-2. ОТЦ_Сх.38.П3.ОИ.М4. Томский университет систем управления и радиоэлектроники

• Название: Томский университет систем управления и радиоэлектроники
• Анкор: Курсовой ОТЦ-2
• Дата: 17.12.2022
• Размер: 0.78 Mb.
• Имя файла: ОТЦ_Сх.38.П3.ОИ.М4.doc
• Тип: Реферат; #848822
• страница: 1 из 3

Министерство образования Российской Федерации


ТОМСКИЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

(ТУСУР)


Кафедра теоретических основ радиотехники

(ТОР)


СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИCТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ


Курсовая работа по дисциплине

“Основы теории цепей”

Студент гр. 142-1

_____И.А.Колесникова

_________
Руководитель

_____В.Д.Дмитриев

_________

2004

Реферат

Курсовая работа 34с., 29 рисунка.

СХЕМНЫЕ ФУНЦИИ ЦЕПИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЦЕПИ, ПОЛОСА ПРОПУСКАНИЯ, ВХОДНОЕ СОПРОТИВЛЕНИЕ, РЕЗОНАНС.

Цель работы – получить и исследовать входные и передаточные операторные функции цепи. Рассчитать частотные характеристики (ЧХ) по выражениям АЧХ и ФЧХ, на основе карты нулей и полюсов (ПНИ) и с использованием автоматизированных методов анализа цепей.

Пояснительная записка к курсовой работе выполнена в текстовом редакторе Microsoft Word XP. с использованием MathCad2000 Professional.

Содержание

1 Введение 5

2 Исходные данные 6

3.Расчетная часть 7

3.1.Исследование нагрузки 7

3.1.1.Предполагаемый на основе схемы характер АЧХ и ФЧХ входной и передаточной функций: 7

3.1.2.Вывод операторных выражений входной и передаточной

функций 9

3.1.3.Нормировка операторных функций 10

3.1.4.ПНИ операторных функций 11

3.1.5.Расчет резонансных частот и резонансных сопротивлений 13

3.2.Исследование транзистора с обобщенной нагрузкой. 15

3.2.1.Вывод операторных выражений на основе МУП 15

3.2.2.Нормировка операторных функций 17

3.3.Исследование транзистора с избирательной нагрузкой 19

3.3.1.Предполагаемый характер ЧХ 19 3.3.2.Получение выражений входной и передаточной функций 21

3.3.3.Предполагаемый ЧХ на основе ПНИ и ЧХ на =1,5 23

3.3.4.Выражения АЧХ и ФЧХ и ЧХ на 28

3.3.5.АЧХ и ФЧХ обеих функций на основе автоматизированного

расчета. 29

3.3.6Определение ППЦ 31

3.3.7.Входное сопротивление полной цепи в виде последовательной и параллельной модели 32

4.Вывод 33

Список использованной литературы 34

1Введение

Комплексная функция цепи (КФЦ) есть отношение комплексной амплитуды отклика к комплексной амплитуде воздействия. Использование комплексных амплитуд свидетельствует о том, что цепь находится в установившемся режиме под гармоническим воздействием.

Все КФЦ принято делить на входные и передаточные. КФЦ называется входной, если воздействие и отклик принадлежат одной и той же паре полюсов: Z(iw), Y(iw); КФЦ называется передаточной, если воздействие и отклик принадлежат разным парам полюсов: K_u(iw), K_J(iw), Z_{l m}(iw), Y_{l m}(iw).

Двухполюсник (цепь с двумя полюсами) описывается только входными функциями. Трех-, четырех-, n- полюсник описывается как входной, так и передаточной КФЦ. Любая КФЦ несет информацию, как об амплитудных, так и о фазовых соотношениях отклика и воздействия; поэтому любая КФЦ может быть представлена в виде двух характеристик: амплитудно-частототной (АЧХ) и фазочастотной (ФЧХ).

Общая методика получения выражения для частотных характеристики цепи состоит в следующем:

-получают выражение интересующей КФЦ,

-находят выражения АЧХ как модуль КФЦ,

-находят выражения ФЧХ как аргумент КФЦ.

Эта методика одинакова для цепей любой сложности.

КФЦ рассчитывается при неопределенном значении частоты любым удобным способом. Несмотря на то, что ЧХ рассчитываются и экспериментально снимаются при гармоническом воздействии, ЧХ позволяют судить о поведении цепи при сложном воздействии как в установившемся, так и в переходном режиме.

Полоса пропускания цепи (ППЦ)- непрерывная область частот, в пределах которой значения АЧХ отличаются от своего максимального значения не более чем в раз или на 3 дБ.

ППЦ может быть определена как на основе графика АЧХ, так и на основе выражения для АЧХ.

Методика определения ППЦ на основе выражения АЧХ состоит в следующем:

-определяется максимальное значение АЧХ-K_max,

-выражение АЧХ приравнивается значению ,

(1.1)

-вычисляются значения граничных частот из равенства (1.1),

-находится полоса пропускания цепи.

2. Исходные данные:

Шифр задания	, Ом	N	k или m	К или КТ
Сх.38П3 ОИ М4	100	0,02	-	-	1.5

Модель полевого транзистора М4в схеме с общим истоком приведена на рисунке 2.1.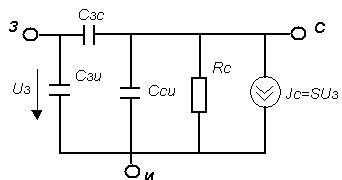



Рисунок.2.1 модель полевого транзистора.

На рисунке 2.2.представлена модель избирательной нагрузки: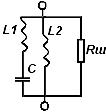



Рисунок.2.2 Модель избирательной нагрузки.
Параметры схемы:





3. Расчетная часть.

3.1.Исследование нагрузки

3.1.1.Предполагаемый на основе схемы характер АЧХ и ФЧХ входной и передаточной функций.

• Входная функция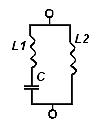


Рисунок 3.1. Модель реактивного двухполюсника.

На рис. 3.1.представлен идеальный реактивный двухполюсник, в котором наблюдается 3 реактивных элемента. На рисунке 3.2 представлены диаграмма реактивного двухполюсника и его модуль на крайних частотах диапазона 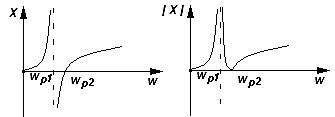и .



(закоротка на L, разрыв на С)

(закоротка на С, разрыв на L)
Рисунок 3.2 Параллельное соединение реактивных элементов.

Т.к. в схеме три реактивных элемента, по теореме Фостера число резонансов n=2.

• 
  Расчет на крайних частотах диапазона входного сопротивления с учетом влияния сопротивлений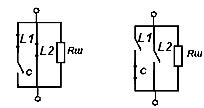
  

Z_ВХ(0)= , Z_ВХ( )= (закор. на С).

Рисунок 3.3. Модели двухполюсника на крайних частотах

На тока в цепи будет протекать через индуктивность L, т.к. она закорочена. При ток протекает по пути меньшего сопротивления, т.е. через сопротивление шунта, величина которого по сравнению с бесконечным сопротивлением очень мала.
Рассмотрим моменты, когда _рез.

а) В момент наступления резонанса токов параллельное соединение двух индуктивностей и ёмкости является разрывом в цепи и ток будет протекать только через сопротивление шунта.

б) Когда же в цепи наступает резонанс напряжений, то вышеуказанное соединение закорачивается, что приводит к падению сопротивления до нуля.

На рисунке 3.4. указаны модели цепей на резонансных частотах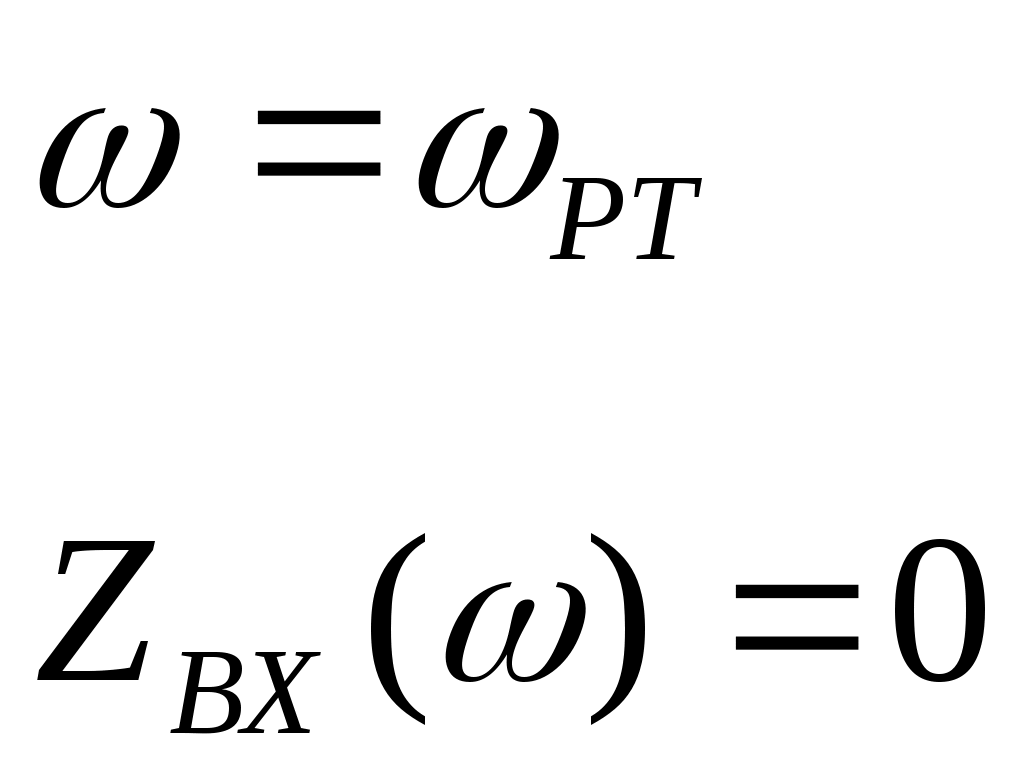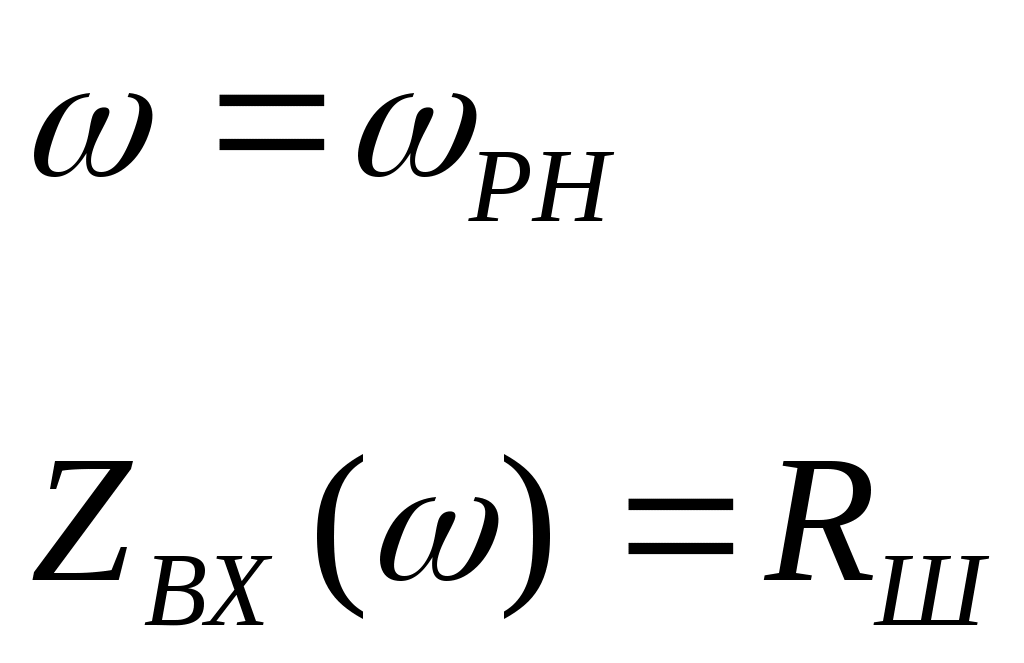




Рисунок 3.4 модели цепей на резонансных частотах

• 
  АЧХ входной функции.
  

На основе проделанных действий построим на рисунке 3.5 предполагаемый характер АЧХ для входного сопротивления: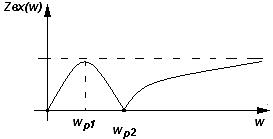



Рисунок 3.5 Предполагаемый характер АЧХ входной функции

• 
  ФЧХ входной функции
  

На основе диаграммы реактивного сопротивления X( ) для параллельного контура сделаем грубую оценку ФЧХ входной функции, которая приведена на рисунке 3.6.



рисунок. 3.6 Грубая оценка ФЧХ входной функции
С учетом того, что на частоте входное сопротивление определяется L1, значит , а на определяется емкостью С и так же того, что при наличии потерь в контуре ФЧХ при переходе через резонансную частоту меняется не скачком, а плавно. на резонансной частоте фазового резонанса всегда равно нулю. Основываясь на этом, построим предполагаемый характер ФЧХ входной функции, который приведен на рисунке 3.7



рисунок. 3.7 Предполагаемый характер ФЧХ входной функции.

3.1.2. Вывод операторных выражений входной и передаточной функций.

Вывод операторных выражений будем проводить используя МУП.

Представим избирательную нагрузку (рис.2.2) в виде: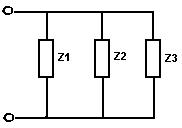



рисунок.3.8 Эквивалентная модель нагрузки

Общее сопротивление цепи при последовательном соединении элементов будет иметь вид:

, где





Т.о. входное сопротивление цепи выглядит следующим образом: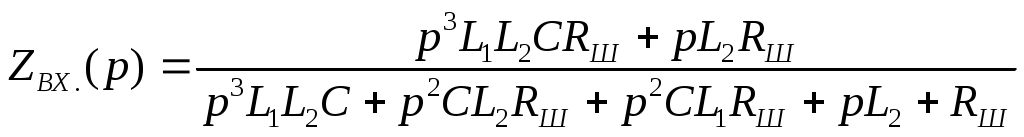




Проверка:

1)Размерность.



2)Крайние частоты.



(по выражению) (по выражению)

3)Порядок.


число реактивностей: 3

число емкостных контуров при подключении источника Э.Д.С.:0; индуктивных сечений:0.

число емкостных контуров при подключении источника тока:0; индуктивных сечений:0.

Таким образом, имеем:



т.к. Z_ВХ на бесконечности определяется сопротивлением, то n=m!
3.1.3. Нормировка операторных функций.
• Ненормированные значения.







• Нормирующие значения.





• Нормировка.












Таблица 3.1

	L1,мкГн	L2,мкГн	C,пФ	RШ,,Ом
Ненормированные величины	2,7	2,7	270,78	1000
Нормированные величины	2	2	1	10

• Нормированные функции.

Входная функция: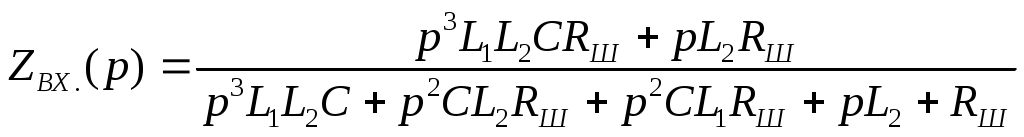





3.1.4. Предполагаемый характер частотных характеристик (ЧХ) на основе ПНИ операторных функций и вычисление значений ЧХ на .
•1. Входная функция


Нули: Полюса: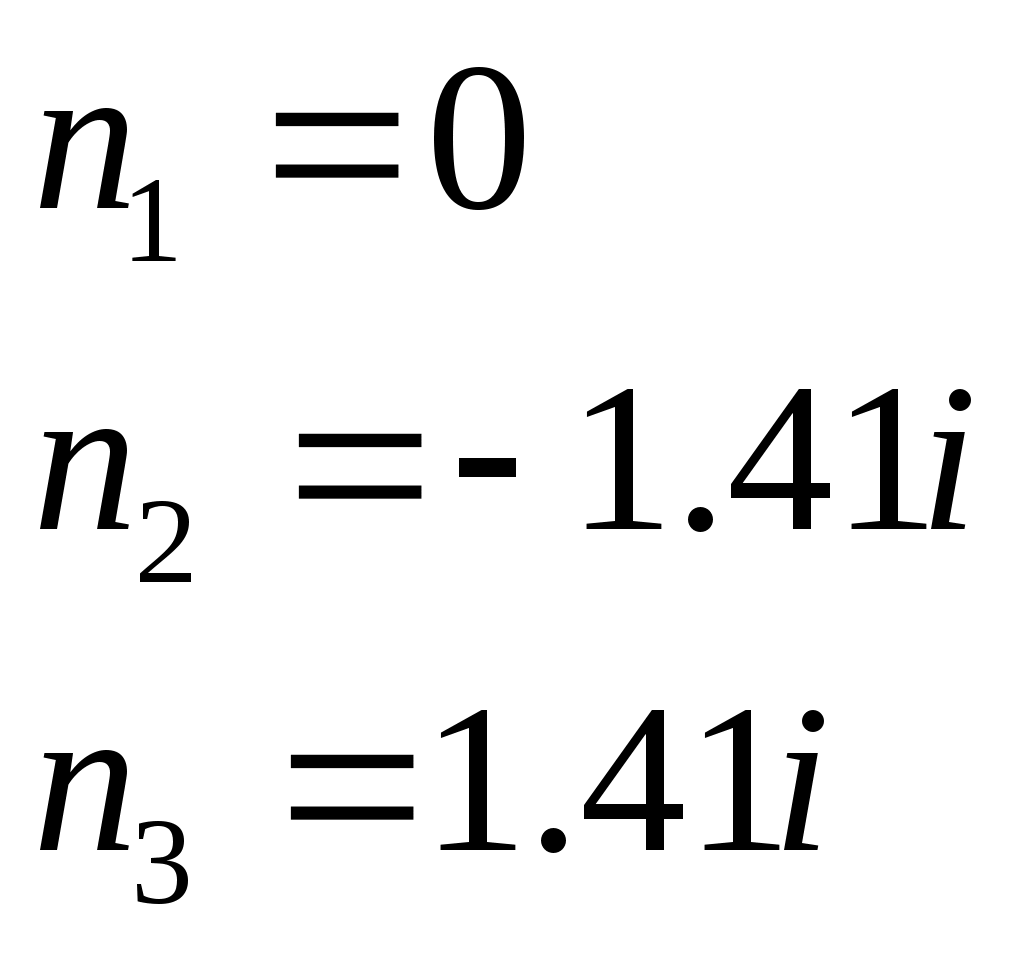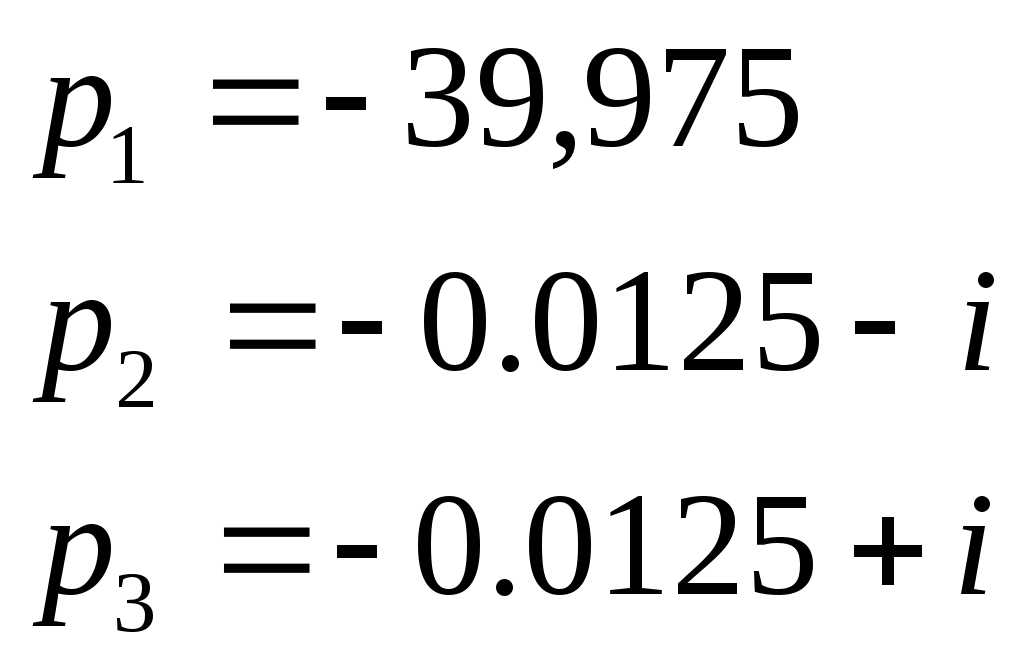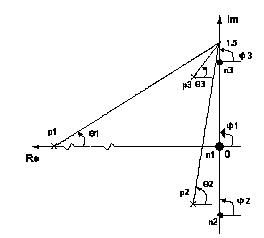




рис. 3.9 ПНИ входной функции.

Таблица 3.2 Длины векторов для заданной частоты .

n1	n2	n3	p1	p2	p3
1,5	2,91	0,09	40	2,5	0,5

Таблица 3.3 Углы для заданной частоты.

φ1	φ2	φ3	Θ1	Θ2	Θ3
90	90	90	2,149	89,714	88,568

Расчет значений АЧХ ФЧХ производится по формулам:

АЧХ:

ФЧX:
На :

АЧХ:

ФЧХ:
Дополнительно рассмотрим случай крайних частот по ПНИ. Имеем, что

На : На

АЧХ: АЧХ:

ФЧХ: ФЧХ:
Построим в MathCad АЧХ и ФЧХ нормированной входной функции и сравним с предполагаемым характером ЧХ и тем, что мы получили, воспользовавшись, ПНИ. На рисунке 3.10 приведен модуль , а на рисунке 3.11 фаза входной функции.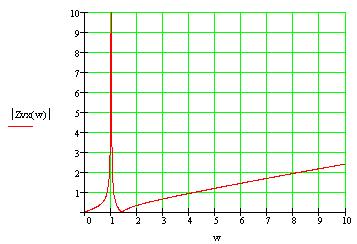



Рисунок. 3.10 АЧХ входной функции.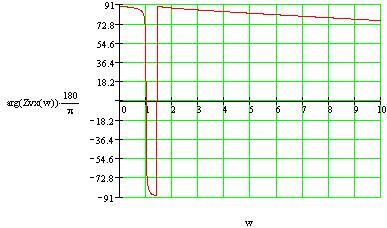



Рисунок. 3.11 ФЧХ входной функции.
Как видно из графиков, наши предположения и вычисления по ПНИ ЧХ на крайних частотах полностью оказались верными, так же совпадает расчет по ПНИ на заданной частоте . Не совпадение происходит только на резонансных частотах в предположительной ЧХ с графиками. Это связано c тем, что большое сопротивлением шунта влияет на характер ЧХ.
3.1.5. Расчет резонансных частот и сопротивлений

Определение резонансной частоты и резонансного сопротивления проводится на основе нормированного выражения Z^Н(p^Н) для нагрузки. В соответствии с определением фазового резонанса на резонансной частоте входное сопротивление является чисто активным и равно следующему:

, таким образом, имеем, что резонансная частота будет равна:

=0

Воспользуемся полученным выражением для входного сопротивления нагрузки :


Сделаем замену:

В результате произведённой замены мы получим следующее выражение:



Найдем корни уравнения, предварительно приравняв его к нулю:

=0,

корни уравнения: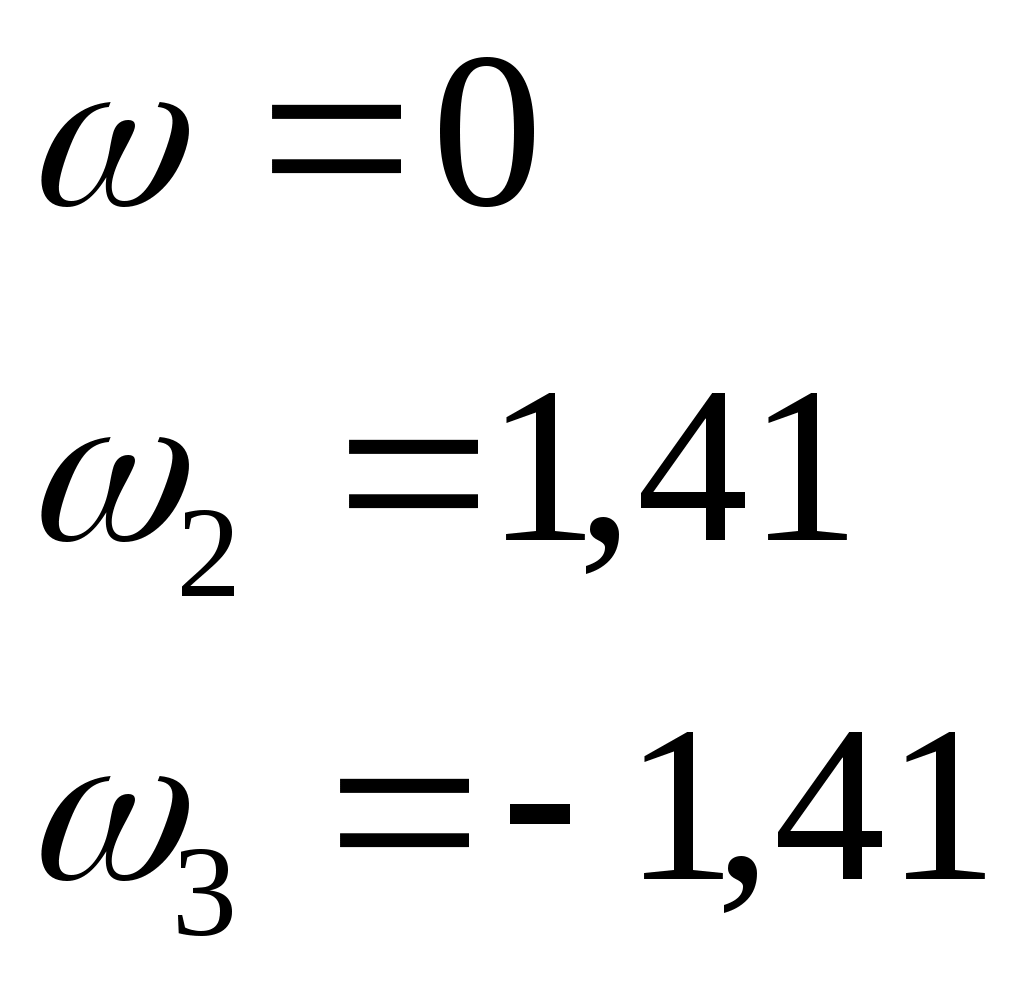