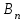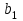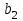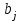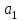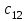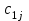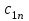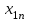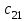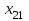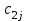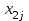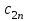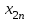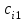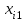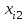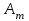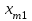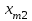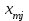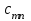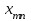Транспортная задача
 Скачать 209 Kb. Скачать 209 Kb.
|
Транспортная задачаТранспортная задача – одна из распространенных задач линейного программирования. Ее цель – разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д. В общем виде задачу можно представить следующим образом: в m пунктах производства 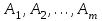 имеется однородный груз в количестве соответственно имеется однородный груз в количестве соответственно 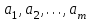 . Этот груз необходимо доставить в n пунктов назначения . Этот груз необходимо доставить в n пунктов назначения  в количестве соответственно в количестве соответственно 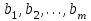 . Стоимость перевозки единицы груза (тариф) из пункта . Стоимость перевозки единицы груза (тариф) из пункта 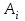 в пункт в пункт 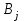 равна равна  . .Требуется составить план перевозок, позволяющий вывезти все грузы и имеющий минимальную стоимость. В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми. Если 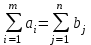 , то задача называется закрытой, в противном случае - открытой. , то задача называется закрытой, в противном случае - открытой.Обозначим через 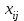 количество груза, перевозимого из пункта количество груза, перевозимого из пункта 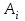 в пункт в пункт 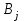 . Рассмотрим закрытую транспортную задачу. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения. . Рассмотрим закрытую транспортную задачу. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения.
Математическая модель закрытой транспортной задачи имеет вид: 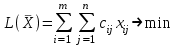 при ограничениях: 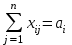  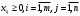 Оптимальным решением задачи является матрица 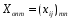 , удовлетворяющая системе ограничений и приводящая целевую функцию к минимальному значению. Транспортная задача как задача линейного программирования может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими. Поэтому для решения транспортных задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно: , удовлетворяющая системе ограничений и приводящая целевую функцию к минимальному значению. Транспортная задача как задача линейного программирования может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими. Поэтому для решения транспортных задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно:нахождение исходного опорного решения; проверка этого решения на оптимальность; переход от одного упорного решения к другому. Рассмотрим каждый их этих этапов. 1. Нахождение исходного опорного решения. Условие задачи и ее исходное опорное решение будем записывать в распределительную таблицу. Клетки, в которые поместим грузы, называются занятыми, им соответствуют базисные переменные опорного решения. Остальные клетки незанятые, или пустые, им соответствуют свободные переменные. В верхнем правом углу каждой клетки будем записывать тарифы. Существует несколько способов нахождения исходного опорного решения. Рассмотрим один из них – метод минимального тарифа (элемента). Согласно этому методу, грузы распределяются в первую очередь в те клетки, в которых находится минимальный тариф перевозок  . Далее поставки распределяются в незанятые клетки с наименьшим тарифом с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем m+n-1. В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми. . Далее поставки распределяются в незанятые клетки с наименьшим тарифом с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем m+n-1. В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми.Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждой строке и столбце было не менее чем по одной занятой клетке. Рассмотрим нахождение исходного опорного решения транспортной задачи на конкретном примере. На складах 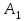 , ,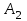 , ,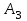 имеются запасы продукции в количествах 90, 400, 110 т. соответственно. Потребители имеются запасы продукции в количествах 90, 400, 110 т. соответственно. Потребители 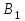 , ,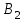 , , должны получить эту продукцию в количествах 140, 300, 160 тонн соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была минимальной. Расходы по перевозке 1 тонны продукции задана матрицей: должны получить эту продукцию в количествах 140, 300, 160 тонн соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была минимальной. Расходы по перевозке 1 тонны продукции задана матрицей: 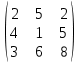 Проверим, является ли данная транспортная задача закрытой: 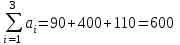 т, т, 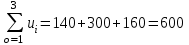 т. Очевидно, т. Очевидно,  , , следовательно, данная транспортная задача закрытая. Найдем исходное опорное решение по методу минимального тарифа.
Число занятых клеток в таблице равно m+n-1=3+3-1-5, т.е. условие невырожденности выполнено. Получили исходное опорное решение, которое запишем в виде матрицы:  Стоимость перевозки при исходном опорном решении составляет  Для нахождения опорного решения можно применить метод северо-западного угла. В данном методе запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика. Заполнение таблицы транспортной задачи начинается с левого верхнего угла (северо-западный угол таблицы) и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель. 2. Проверка найденного опорного решения на оптимальность. Найденной исходное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система m+n действительных чисел  и и  , удовлетворяющих условиям , удовлетворяющих условиям 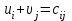 для занятых клеток для занятых клеток 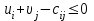 для свободных клеток. для свободных клеток.Числа  и и 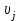 называют потенциалами. В распределительную таблицу добавляют строку называют потенциалами. В распределительную таблицу добавляют строку 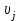 и столбец и столбец  . .Потенциалы  и и 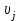 находят из равенства находят из равенства 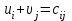 , справедливо для занятых клеток. Одному из потенциалов дается произвольное значение, , справедливо для занятых клеток. Одному из потенциалов дается произвольное значение, 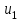 =0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал =0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал  , то , то 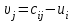 , если известен потенциал , если известен потенциал 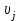 , то , то 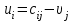 . .Обозначим  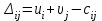 . Эту оценку называют оценкой свободных клеток. Если . Эту оценку называют оценкой свободных клеток. Если 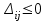 , то опорное решение является оптимальным. Если хотя бы одна из оценок , то опорное решение является оптимальным. Если хотя бы одна из оценок 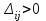 , то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому. , то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец  и строку и строку 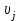 . .Полагая 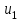 =0, запишем это значение в последнем столбце таблицы. =0, запишем это значение в последнем столбце таблицы.
Найдем оценки свободных клеток.  =3+0-5=-2, =3+0-5=-2, 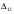 =7+0-2=5, =7+0-2=5, 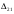 = 2-2-4=-4, = 2-2-4=-4, 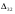 =3+1-6=-2. =3+1-6=-2.Найденное опорное решение не является оптимальным, так как оценка 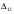 =5. =5. 3. Переход от одного опорного решения к другому. Наличие положительной оценки свободной клетки 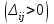 при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому к другому опорному решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной. при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому к другому опорному решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной.Для свободной клетки с 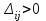 строится цикл (цепь, многоугольник), все вершины которого кроме одной находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляются знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают у грузов у вершин со знаком (-). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т.д. до тех пор, пока не получим оптимальное решение. строится цикл (цепь, многоугольник), все вершины которого кроме одной находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляются знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают у грузов у вершин со знаком (-). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т.д. до тех пор, пока не получим оптимальное решение.Рассмотрим переход от одного опорного решения к другому на заданном примере. Строим цикл для клетки (1,3), имеющей положительную оценку. У вершин цикла ставим знаки (+) и (-) и записываем грузы:  У вершин со знаком (-) выбираем минимальный груз, он равен 60. Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл.  Новое опорное решение  . .Проверим полученные решения на оптимальность. Для этого запишем его в распределительную таблицу, найдем потенциалы занятых и оценки свободных клеток.
Имеем: 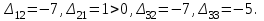 Построим цикл для клетки с положительной оценкой 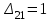   Произведем перераспределение грузов:  Получим новое решение, которое занесем в таблицу и проверим его на оптимальность.
Получим:  Все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное. Итак, 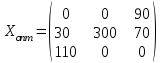 Стоимость транспортных расходов равна 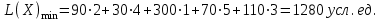 По сравнению с исходным опорным решением транспортные расходы уменьшились на 1610-1280=330 усл. ед. Применение транспортной задачи для решения экономических задач. Задача о размещении производства с учетом транспортных затрат. Пусть имеется или проектируется m пунктов производства с объемами производства 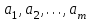 и n пунктов потребления с объемами потребления и n пунктов потребления с объемами потребления 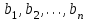 . Затраты на производство единицы продукции в каждом i-м пункте производства известны и равны . Затраты на производство единицы продукции в каждом i-м пункте производства известны и равны 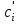 , ,  . Стоимости перевозки единицы груза от каждого i–го производителя каждому j–му потребителю известны и равны . Стоимости перевозки единицы груза от каждого i–го производителя каждому j–му потребителю известны и равны  , ,  , , 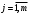 . Суммарные объемы производства превосходят суммарные объемы потребления. Требуется составить план сокращения (размещения) производства, обеспечивающий минимальные производственно-транспортные затраты. . Суммарные объемы производства превосходят суммарные объемы потребления. Требуется составить план сокращения (размещения) производства, обеспечивающий минимальные производственно-транспортные затраты.Задача решается как транспортная задача, матрица стоимостей которой составляется как сумма матриц: С=(  )=( )=(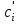 + + ), ), , , 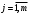 . . Вводится фиктивный потребитель. Затем задача решается обычным способом. Далее сокращается производство в пунктах, продукция которых в оптимальном плане перевозок поставляется фиктивному потребителю. Задача о назначениях, или проблема выбора. Пусть имеется m групп людей (станков) численностью 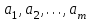 , которые должны выполнять nвидов работ (операций) объемом , которые должны выполнять nвидов работ (операций) объемом 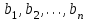 . Известна производительность каждой i–й группы людей (станков) при выполнении каждого j–го вида работ (операций) . Известна производительность каждой i–й группы людей (станков) при выполнении каждого j–го вида работ (операций)  , ,  , , 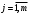 . . Требуется так распределить людей (станки) для выполнения работ (операций), чтобы суммарный объем производства работ (операций) был максимальным. . . Требуется так распределить людей (станки) для выполнения работ (операций), чтобы суммарный объем производства работ (операций) был максимальным.Составим математическую модель данной задачи по аналогии с транспортной задачей. Обозначим 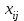 - число людей (станков) i–й группы, занятых j–го вида работ (операций). Запишем математическую модель. Целевая функция - число людей (станков) i–й группы, занятых j–го вида работ (операций). Запишем математическую модель. Целевая функция 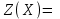   , с ограничениями , с ограничениями 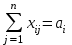 , , , ,  , , 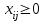 , ,  , , 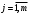 , , Для использования алгоритмов, разработанных для транспортной задачи, можно перейти от нахождения максимума к нахождению минимума. Для этого нужно умножить коэффициенты целевой функции на (-1), тогда целевая функция будет иметь вид 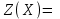 - -  . .Можно также изменить критерий оптимальности. Например, вместо 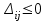 для всех i, ,j использовать новый критерий оптимальности для всех i, ,j использовать новый критерий оптимальности 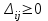 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||