конспект урока. Конспект урока по геометрии в 8 классе на тему «Трапеция. Средня. Трапеция. Средняя линия трапеции

• Название: Трапеция. Средняя линия трапеции
• Анкор: конспект урока
• Дата: 26.10.2022
• Размер: 61.5 Kb.
• Имя файла: Конспект урока по геометрии в 8 классе на тему «Трапеция. Средня.doc
• Тип: Урок; #756025

Тема урока: Трапеция. Средняя линия трапеции.(слайд 1)

Цель урока:
образовательные: формировать навыки решения задач с применением теоремы Фалеса, свойств трапеции в зависимости от её вида, теоремы о средней линии трапеции; решать задачи по готовым чертежам;
развивающие: развитие навыков логического мышления учащихся, память, вычислительные навыки, умение применять полученные знания на практике

воспитательные: формировать самостоятельность, воспитывать познавательную активность, внимательность, аккуратность, дисциплинированность, интерес к изучению математике.

Ход урока

I. Организационный момент.

II. Проверка домашнего задания.

В равнобедренную трапецию, боковая сторона которой равна 23 дм, вписана окружность. Найти среднюю линию трапеции.

III. Повторение основных понятий, теорем.

1)Нужно назвать каждый из четырехугольников и дать понятие четырехугольнику:

(слайд 2-5)

Какой четырех угольник называется трапецией? Как называются стороны трапеции?

Какая трапеция называется прямоугольной? Равнобедренной?

Сформулируйте свойства равнобедренной трапеции.

Сформулируйте признаки равнобедренной трапеции.

Что такое средняя линия трапеции? Сформулируйте свойство средней линии трапеции.

Виды трапеций.

Если предложение верное, то «+» в столбце «А»; если неверное «+» в столбце «В», а если ученик не может ответить верно или нет, то ответ записывает в столбец «С».

1. 
   Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. (А).
   
2. 
   Трапецией называется четырехугольник, у которого противоположные стороны параллельны. (В).
   
3. 
   В любом треугольнике можно провести только одну среднюю линию. (В).
   
4. 
   Средняя линия трапеции параллельна основаниям и равна их полу сумме. (А).
   
5. 
   У равнобокой трапеции углы при основании равны. (А)
   
6. 
   В прямоугольном треугольнике с углом в 30° катет, противолежащий этому углу, равен половине гипотенузы. (А).
   
7.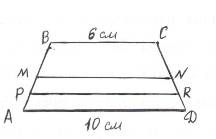 
   У равностороннего треугольника все углы разные. (В).
   
8. 
   Треугольник называется прямоугольным, если у него есть гипотенуза. (В).
   

IV Решение упражнений

1. 
   (слайд 6)Решение задач устно по готовому чертежу.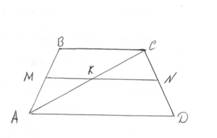
   

MN – средняя линия трапеции АВСD,
PR –  средняя линия трапеции АMND.
ВС = 6 см., АD= 10 см.
Найдите: MN и PR.

2. 
   (слайд 7)Чем являются отрезки МК и КN, если MN – средняя линия трапеции АВСD?
   

Работа по формированию навыков решения задач (на каждый стол посередине положен листок с напечатанными задачами) .(слайд 8)

3.Большее основание трапеции равно 8см, а меньшее на 3см меньше средней  линии. Найти основания трапеции.

4.В равнобокой трапеции диагональ делит острый угол пополам. Периметр её равен 54дм, большее её основание  - 1,8м. Вычислите меньшее основание трапеции.

Задача 3.
Большее основание трапеции равно 8см, а меньшее на 3см. меньше средней  линии.



Дано:         
АВСД – трапеция
АД = 8см.
МК – средняя линия
ВС -? на 3см меньше МК
______________________
ВС –?  МК - ?

Решение:
Пусть ВС = х см, тогда МК = (х+3)см
МК = АД + ВС/2,   х+3 =  х+8 /2 ,     2х+6 =х+8 , х=2

ВС =2см, 1) 2+3 = 5(см)
Ответ: ВС = 2см, МК = 5см.

Задача 4
В равнобокой трапеции диагональ делит острый угол пополам. Периметр её равен 54дм,
большее её основание  - 1,8м. Вычислите меньшее основание трапеции.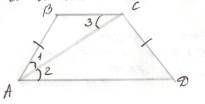



Дано:
АВСД – равнобокая трапеция
Р -54дм.
АД = 1,8м = 18дм.
___________________
ВС -?

Решение:
∠1 = ∠2     т.к. АС – биссектриса ∠A
∠2 = ∠3 как внутренние накрест лежащие углы.
∠1 = ∠2 и ∠2 = ∠3 ⇒ ∠1 = ∠3 ⇒ ∆ АВС - равнобедренный

Пусть АВ = ВС =СД = х
Уравнение
3х+18 = 54
3х =54-18 
3х = 36
х =12
Ответ: ВС =12дм.

Л	С
И	О
Т	К

3. Математическая минутка. (слайд 9)
Отгадайте, какое слово зашифровано(столик).
Трапеция (от греческого слова trapezion- буквальный перевод – столик)

4. Решение задач по готовому чертежу.

5) (слайд 10)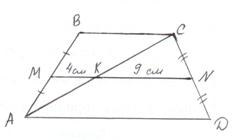

ВС - ? АД - ? если МК = 4см, KN = 9см.

6) (слайд 11)

Дано: АВСД –трапеция,   МN – средняя линия,   ВС : АД = 2 : 3, MN = 5 см.
Найти: ВС - ? АД - ?

Решение:
Пусть  x см – 1 часть, тогда ВС = 2x см, АД = 3х см.
MN = (ВС + АД) / 2,  5 = (2x + 3x) / 2, 5х = 10   х = 2

1. 
   2*2 = 4 см.
   
2. 
    2*3 = 6 см.
   

Ответ: ВС = 4 см, АД = 6 см.

7. Подведение итогов урока

Домашнее задание: (слайд 12)

Меньшее основание трапеции равно 14см, а большее на 5см больше средней  линии. Найти основания трапеции.