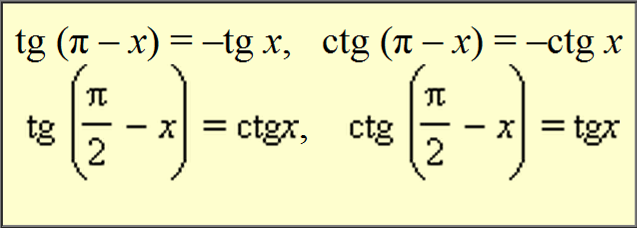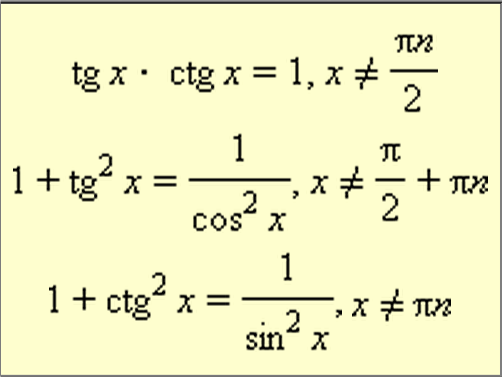|
|
открытый урок. Тригонометрические функции и их свойства и графики. Тригонометрические функции и их свойства и графики
Краткосрочный план
Тригонометрические функции и их свойства и графики
|
Школа ФМН НИШ Алматы
|
Дата:
|
ФИО учителя:
|
Класс: 10
|
Количество
|
присутствующих:
|
отсутствующих:
|
Тема урока
|
Тригонометрические функции и их свойства и графики
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
10.2.3.1 знать определения, свойства тригонометрических функций и уметь строить их графики
|
Цели урока
|
Учащиеся будут:
отрабатывать навыки исследовательской культуры учащихся на уроке, закрепить знания, полученные на предыдущем уроке, продолжить изучение темы.
- область определения и область значений, т.к. для синуса и косинуса есть ограничения по области значений, а для тангенса и котангенса ограничения по области определения;
отработать навыки построения графиков функций, используя периодичность тригонометрических функций;
закрепить изученный материал о чётных и нечётных функциях
периодичность всех тригонометрических функций, т.к. мы уже отмечали наличие наименьшего ненулевого аргумента, добавление которого не меняет значение функции. Такой аргумент называют периодом функции и обозначают буквой  . Для синуса/косинуса и тангенса/котангенса эти периоды различны. . Для синуса/косинуса и тангенса/котангенса эти периоды различны.
|
Критерии оценивания
|
Учащийся:
знает:
понятие тригонометрической функций;
что такое тангенс и котангенс;
область определения тангенса и котангенса;
область значения тангенса и котангенса;
графики тангенса и котангенса:
значения тангенса и котангенса при градусной мере;
.
|
Языковые цели
|
Учащиеся будут:
аргументировать свои выводы, работая в группе, при повторении теоретического материала на более высоком уровне;
описывать ход своих действий и делать выводы
владеть математической терминологией данного урока;
при устной работе обосновывать ответ, используя терминологию;
комментировать приведение подобных слагаемых;
комментировать выполнение тождественных преобразований алгебраических выражений
Предметная лексика и терминология:
тангенс и котангенс;
графики;
тригонометрия;
область определения;
множество значения;
подобные слагаемые;
тождественные преобразования выражений;
упрощение тригонометрических функций
|
Привитие ценностей
|
Умение учиться, добывать самостоятельно информацию, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время.
Привитие ценностей осуществляется посредством работ, запланированных на данном уроке.
|
Межпредметные связи
|
Взаимосвязь с жизнью, через решение практических задач, геометрия
|
Предварительные знания
|
Треуголник, градусные и радианные меры угла. Соотношения сторон треуголника.
|
Ход урока:
Запланированные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
0 – 3 мин
|
Организационный момент. Актуализация опорных знаний
Проверить домашнее задание.
Устный опрос.
Чем различается синуc угла от косинуса?
Как можно выражать синус используя косинус? Или наоборот?
Совместно с учащимися определить тему и цели урока, зону ближайшего развития.
|
Презентация
|
Середина урока
4 - 12 мин
|
Работа с классом. Ввод новой темы. I) Историческая справка
 тригонон тригонон
 Тригонометрия Тригонометрия
метрио
(измерение треугольника)
Древний Вавилон-умели предсказывать солнечные и лунные затмения.
Древнегреческие учёные-составили таблицы хорд(первые тригонометрические таблицы)
Учёные Индии и Ближнего Востока-положили начало радианной мере угла.
Древний Вавилон-умели предсказывать солнечные и лунные затмения.
Древнегреческие учёные-составили таблицы хорд(первые тригонометрические таблицы)
Учёные Индии и Ближнего Востока-положили начало радианной мере угла.
Гиппарх
Птолемей
Франсуа Виет
Эйлер
Бернулли
Определение тангенса и котангенса:
Тангенсом угла x называется отношение синуса этого угла к косинусу этого же угла.
Котангенсом угла x называется отношение косинуса этого угла к синусу этого же угла.
Теперь изучим свойства тангенса и котангенса:
 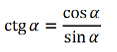
Тангенс и котангенс являются периодическими функциями.
Их основной период равен π.
Значения этих функций в некоторых точках приведены
в таблице.

Промежутки монотонности и знакопостоянства. Функции tg x и ctg x нечетны.

Формулы приведения тангенса и котангенса
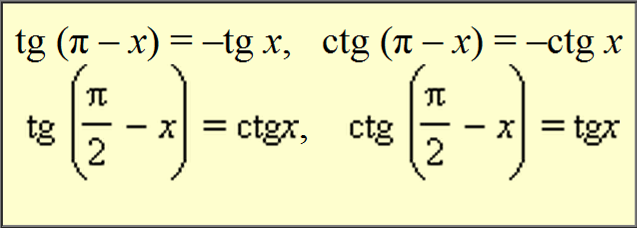
Тождества, связанные с тангенсами и котангенсами.
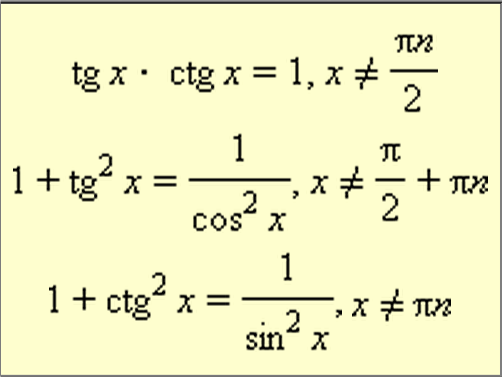
График функций y = tg x
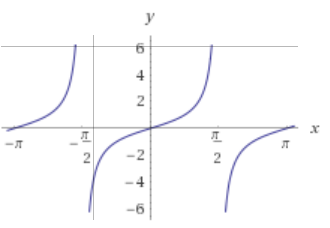
График функций y = сtg x
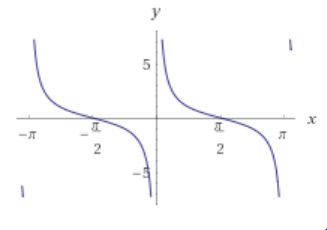
|
Приложение 1
|
|
Середина урока
13 - 30 мин
|
Индивидуальная работа. Для закрепления материала предложить решить задания Приложения 1. Каждый выполняет самостоятельно.
После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении.
|
Приложение 2
|
Середина урока
31 - 37 мин
|
Групповая работа.
Объединить учащихся в разноуровневые группы по 4 - 6 учеников. Раздать каждой группе карточки с заданиями Приложения 2.
Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.
Предоставить учащимся достаточно времени для выполнения заданий.
Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения задания..
Старший группы оценивает вклад каждого, выставляя отметку.
|
Приложение 3
|
Конец урока
38 - 40 мин
|
Беседа. Рефлексия. Учащиеся в конце урока определяют свою успешность и отношение к уроку.
Н  а уроке мне На уроке мне не а уроке мне На уроке мне не
понравилось…. понравилось….
Домашнее задание. Знать определения, решить из уровня В.
|
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
|
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
|
Здоровье и соблюдение техники безопасности. Связи с ИКТ.
|
На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности.
|
Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. Используется наблюдение за действиями учащихся, обсуждением результатов выполнения заданий.
Взаимооценивание. Самооценивание при рефлексии.
|
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся.
|
Приложение 1
tg (-t) =
ctg (-t) = .
tg(t+p ) =
tg(t+ 3p/2) =
ctg(t+ p/2 ) =
ctg(t+p ) =
Приложение 2
1) Найдите значение выражения
24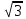 tg(− 750°)=? tg(− 750°)=?
2) Найдите значение выражения
4tg(−3π – t) – 3tg t, если tg t = 1.
3) Найдите  , если tg t = 1 , если tg t = 1 |
|
|
 Скачать 378.79 Kb.
Скачать 378.79 Kb. tg(− 750°)=?
tg(− 750°)=? , если tg t = 1
, если tg t = 1