|
Урок по алгебре _синус, косинус, тангенс и котангенс произвольно. Синус, косинус, тангенс и котангенс произвольного угла. Значения синуса, косинуса, тангенса и котангенса произвольного угла
Краткосрочный план
Раздел долгосрочного план: Раздел 9.3А. Тригонометрия
|
Школа: ГУ «школа-гимназия № 18»
|
Дата:
|
ФИО учителя: Зубко Е.Ф.
|
Класс: 9
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Синус, косинус, тангенс и котангенс произвольного угла. Значения синуса, косинуса, тангенса и котангенса произвольного угла.
|
Цели обучения, которые достигаются на данном уроке
|
9.2.4.1 знать определения основных тригонометрических функций и уметь определить их свойства по единичной окружности;
|
Цели урока
|
Ввести понятия синуса, косинуса и тангенса угла, актуализировать знания о синусе, косинусе и тангенсе угла в прямоугольном треугольнике, ознакомить с основным тригонометрическим тождеством, формулами приведения и формулой для нахождения координат точки, научить применять их при решении задач;
|
Критерии оценивания
|
Учащийся:
-знает определения основных тригонометрических функций и умеет определять их свойства по единичной окружности;
|
Языковые цели
|
Учащиеся будут:
- описывать свойства тригонометрических функций по графическому изображению;
Предметная лексика и терминология
тригонометрическая функция;
синус, косинус, тангенс, секанс, косеканс, котангенс произвольного угла;
Полезные выражения для диалогов и письма:
график y = а sin x сжимается вдоль оси ординат при …
растяжение графикаy = acos x вдоль оси ординат зависит от …
множительa<0отображает график y = asin xсимметрично …..
график функции y= sinb x при b>1 ….
при 0<n<1график функцииy = cos n x растягивается вдоль оси …
y= sin (x-m)переносит график параллельно вдоль … ,
|
Привитие ценностей
|
Умение учиться, добывать самостоятельно информацию, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время.Привитие ценностей осуществляется посредством работ, запланированных на данном уроке.
|
Межпредметные связи
|
На данном уроке рассматриваются понятия, которые необходимы при различных вычислениях на уроках естественно- математического направления.
|
Предварительные знания
|
Градусная и радианная мера угла
|
Ход урока
|
Запланированные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Организация урока
0 -2 мин
|
Приветствие. Отметка отсутствующих. Проверка готовности учащихся к уроку.Совместно с учащимися определяем цели урока и ожидаемые результаты.
Разбор домашнего задания. Учащиеся обмениваются домашним заданием и выполняют проверку по готовым решениям.
|
|
Середина урока
3 -15мин
|
Изучение нового материала.
Введём прямоугольную систему координат Оху и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах. Назовём её единичной полуокружностью.
Из точки О проведём луч, пересекающий единичную полуокружность в точке М(х;у). Обозначим 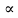 угол между лучом Ом и положительной полуосью абсцисс. угол между лучом Ом и положительной полуосью абсцисс.
Если α- острый , то из ∆ОММ1 имеем: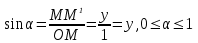 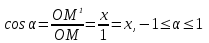
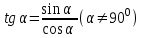 . Итак, синус острого угла равен ординате у точки М, а косинус угла α- абсциссе точки М. Если угол α прямой, тупой или развёрнутый или α=00, то синус, косинус угла α также определяем по данным формулам. Т.О., для любого угла α из промежутка от 00 до 1800 синусом угла α называется ордината у точки М, а косинусом угла α- абсцисса точки М. . Итак, синус острого угла равен ординате у точки М, а косинус угла α- абсциссе точки М. Если угол α прямой, тупой или развёрнутый или α=00, то синус, косинус угла α также определяем по данным формулам. Т.О., для любого угла α из промежутка от 00 до 1800 синусом угла α называется ордината у точки М, а косинусом угла α- абсцисса точки М.
Тренировочные упражнения. Учащимся предлагаются различные задачи для закрепления из учебного пособия. Дифференцированный подход осуществляет учитель (уровень B или C).
Раздаточный материал должен содержат задачи с запасом на более способных
Задания:
Определите знак
функции: 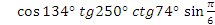 ? ?
Переведите радианную меру угла в градусную: 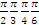 . .
Найдите при помощи круга значение функций, объясните ответ: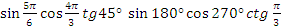 . .
Найдите при помощи круга значение синуса, косинуса, тангенса, если величина угла равна: 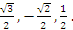
|
|
Середина урока
16 -27 мин
|
Решение упражнений, работа по учебнику.
Работа по решению упражнений идет у доски с вызовом учащихся и на местах. Каждое задание при наличии времени желательно разобрать перед решением.
1 задание:
а) 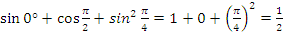
б) 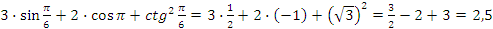
2 задание:
а) 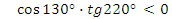
б) 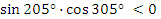
в) 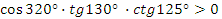
г) 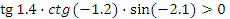
3 задание: № 7 (а) по учебнику.
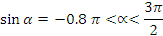
Найдите: 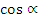 , , 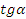 , , 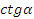 . .
Решение.
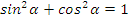 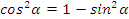
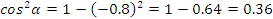
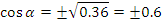
Так угол лежит в 3 четверти, то 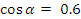
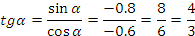 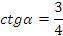 Ответ: 0,6 ; Ответ: 0,6 ; ; ;  . .
|
|
Середина урока
мин
|
Самостоятельная работа на проверку усвоения цели обучения.На данном этапе у учащихся развивается такая ценность академическая честность
После выполнения заданий, учащиеся проводят взаимопроверку правильности выполнения заданий по образцу, выданному учителем.
Задания для самостоятельной работы.
I вариант.
Выразите в градусной мере величину угла: 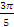 . .
Выразите величину угла в радианах: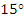 . .
Найдите знак произведения, используя правило знаков по четвертям: 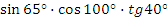 . .
Вычислите значение выражения: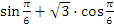 . .
Найдите значение функции 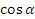 , если , если 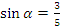 и и 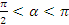 . .
II вариант.
Выразите в градусной мере величину угла: 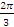 . .
Выразите величину угла в радианах: 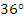 . .
Найдите знак произведения, используя правило знаков по четвертям: 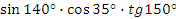 . .
Вычислите значение выражения: 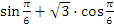 . .
Найдите значение функции 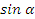 , если , если 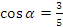 и и 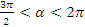 . .
Учащиеся обмениваются листками и проводят самооценивание и взаимооценивание.
|
|
Конец урока
38-40 мин
|
Подведение итогов урока. Рефлексия.
Провести беседу с учащимися.
Что узнал, чему научился?
Какой этап урока был для вас наиболее сложным?
|
|
Дифференциация – как Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
|
Оценивание – как Вы планируете проверить уровень усвоения материала учащихся?
|
Межпредметные связи
Здоровье и безопасность
Связи с ИКТ
Связи с ценностями (воспитательный элемент)
|
Группы учащихся организованны по схеме «Сильный – слабый», что позволяет слабым ученикамулучшать свои навыки, а сильным учащемся совершенствовать свои, осуществляя оценку деятельности других и корректировку знаний.
|
Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат решения задачи.
|
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся.
| |
|
|
 Скачать 65.07 Kb.
Скачать 65.07 Kb.