доклад. Тригонометрическими суммами назывются суммы вида
 Скачать 119.34 Kb. Скачать 119.34 Kb.
|
1 2 ВВЕДЕНИЕТригонометрическими суммами назывются суммы вида 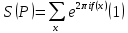 где суммирование распространено на все целые или часть целых из некоторого интервала, P-число слагаемых и f(x) – произвольная функция, принимающая при целых x действительные значения. К изучению таких сумм могут быть сведены многие вопросы теории чисел и ее приложений. где суммирование распространено на все целые или часть целых из некоторого интервала, P-число слагаемых и f(x) – произвольная функция, принимающая при целых x действительные значения. К изучению таких сумм могут быть сведены многие вопросы теории чисел и ее приложений.Покажем, например, как возникают тригонометрические суммы при решении вопроса о возможности представить натуральное число N в виде суммы одинаковых степеней натуральных чисел N = 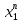 + ... + + ... + 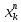 (2) (2)(проблема Варинга ) . Пусть n , k и N – фиксированные натуральные числа , P – наибольшее целое, не превосходящее 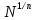 , и , и 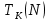 – число решений уравнения (2) . При целом – число решений уравнения (2) . При целом 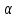 определим функцию определим функцию 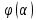 с помощью равенства с помощью равенства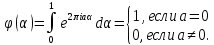 Тогда, очевидно , 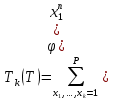 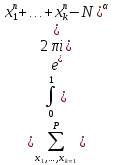 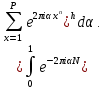 Таким образом, арифметическая задача о числе решений уравнения (2) сводится к исследованию интеграла, зависящего от степени тригонометрической суммы 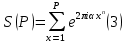 . . Наиболее важны для приложений суммы, в которых функция f(x) является полиномом , а область суммирования предcтавляет собой некоторый интервал: 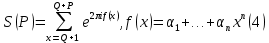 Такие тригонометрические суммы называются суммами Вейля, а степень полинома f(x) – степенью суммы Вейля . Так, например, сумма (3) , возникающая в проблеме Варинга , является суммой Вейля степени n. Центральной задачей теории тригонометрических сумм является получение возможно более точных верхних оценок для модуля тригонометрической суммы. Так как модуль каждого слагаемого суммы равен единице, то для всякой суммы (1) справедлива тривиальная оценка 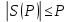 . .Первые общие нетривиальные оценки сумм (4) принадлежат Г. Вейлю. При определеных требованиях к старшему коэффиценту полинома f(x) им было показано , что при любом 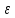 из интервала 0 из интервала 0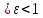 справедливо оценка справедливо оценка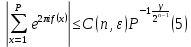 где 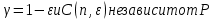 . Существенное усилиние этого результата при n . Существенное усилиние этого результата при n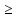 12 , было получено И. М. Виноградовым 12 , было получено И. М. Виноградовым  , показавшим, что в оценке (5) при некотором , показавшим, что в оценке (5) при некотором 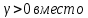 C(n, C(n, 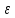 ) )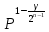 можно поставить величину C(n) можно поставить величину C(n)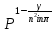 . .Если дробные доли функции f(x) имеют целочисленный период, т.е. если при некотором натуральном 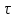 для всякого целого x выполняется равенство для всякого целого x выполняется равенство 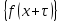 = =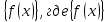 - дробная доля функции f(x), то - дробная доля функции f(x), то сумма 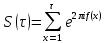 называется полной тригонометрической суммой. Примером полной тригонометрической суммы может служить сумма Вейля, в которой все коэффициенты полинома f(x) рациональны и число слагаемых равно общему знаменателю этих коэффициентов: 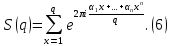 При 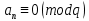 такие суммы называются польными рациональными суммами степени n. Для них известны более точные оценки , чем оценки сумм Вейля оющего вида. такие суммы называются польными рациональными суммами степени n. Для них известны более точные оценки , чем оценки сумм Вейля оющего вида. Всестороннее исследование полных рациональных сумм второй степени было проведено Гауссом. В частности , им было показано, что при (a,q)=1 для модуля суммы 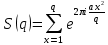 выполняется равенства 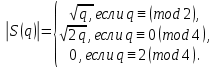 Для полных рациональных сумм произвольной степени при простом q Морделлом было получена оценка 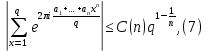 где C(n) не зависит от q . Хуа Ло-ген распространил эту оценку на случай произвольного натурального q. Существенное усиление результата Морделла было получено А. Вейлем, показавшим, что при простим q модуль суммы (7) не превосходит величины (n-1) 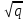 . При фиксированном n и возрастающем qоценки А. Вейля и Хуа Ло-гена является по порядку роста предельно точными и не допускают уже дальнейшего усиления. . При фиксированном n и возрастающем qоценки А. Вейля и Хуа Ло-гена является по порядку роста предельно точными и не допускают уже дальнейшего усиления.Примером полных сумм, отличных от полных рациональных сумм (6), является тригонометрические суммы с показательной функцией 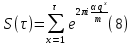 где ( q, m)=1 и 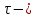 показатель, которому q принадлежит по модулю m. К оценкам таких сумм и сумм S(P) с показатель, которому q принадлежит по модулю m. К оценкам таких сумм и сумм S(P) с 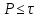 сводится вопрос о числе появлений фиксированной группы знаков среди первых P знаков периодической дроби, возникающей при записи произвольного рационального числа сводится вопрос о числе появлений фиксированной группы знаков среди первых P знаков периодической дроби, возникающей при записи произвольного рационального числа 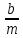 в q- ичной системе счисления. Величина суммы (8) зависит от характера разложения m на простые сомножители и для полных сумм в большинстве случаев оказывается равной нулю. Если же в q- ичной системе счисления. Величина суммы (8) зависит от характера разложения m на простые сомножители и для полных сумм в большинстве случаев оказывается равной нулю. Если же 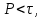 при при 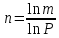 и m равном степени простого числа, выполняется оценка и m равном степени простого числа, выполняется оценка 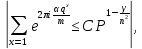 где C и  абсолютные константы. абсолютные константы.Необходимость оценивать тригонометрические суммы возникает и в вопросе о приближенном вычислении интегралов произвольной кратности . Рассмотрим, например, квадратную формулу, постренную с помощью произвольной сетки 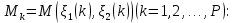 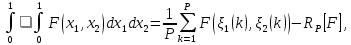 (9) (9)где F( 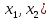 – периодическая функция, заданная абсолютно сходящимся рядмом Фурье: – периодическая функция, заданная абсолютно сходящимся рядмом Фурье: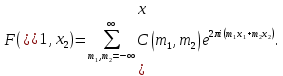 Подставляя этот ряд в равенство (9), после перемены порядка суммирования получим 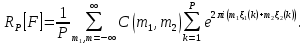 где 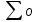 значает что суммирование по всем значает что суммирование по всем 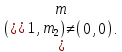 Отсюда следует, что для погрешности квадратурной формулы (9) выполняется оценка 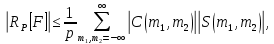 где тригонометрическая сумма 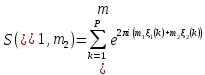 Определяется заданием сетки M 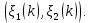 Выбирая функции Выбирая функции 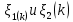 так, чтобы суммы S так, чтобы суммы S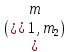 оценивались достаточно хорошо, мы получаем возможность строить квадратурные формулы высокой точности. оценивались достаточно хорошо, мы получаем возможность строить квадратурные формулы высокой точности.Первая глава книги содержит подробное изложение начальных сведений из теории полных тригонометрических сумм и сумм, оценки которых сводятся к оценкам полных сумм. Теоремы, помещенные в этой главе, сравнительно просты, однако они составляют фундамент теории тригонометрических сумм общего вида и служат необходимой подготовкой к более сложным построениям второй главы. Для иллюстрации возможных приложений полных сумм в первой главе дано решение вопроса о распределении знаков в периоде систематических дробей, возникающих при записи рациональных чисел в произвольной системе счисления. Вторая глава технически значительно сложнее первой. Она посвящена изложению теории сумм Вейля общего вида. Наряду с основополагающими методами Вейля и Виноградова в ней изложены исследования, основанные на повторном применении теоремы о среднем, и дано их приложение к оценкам сумм, возникающих в теории дзета-функции Римана  В третьей главе рассматриваются приложения тригонометрических сумм к распределению дробных долей и построению квадратурных формул. В ней изложена созданная Вейлем теория равномерного распределения, рассмотрены вопросы вполне равномерного распределения, и их связи с теорией нормальных чисел. Заключительная часть главы посвящено вопросу о приближенном вычислении кратных интегралов и построению интерполяционных формул для функций многих переменных  Суммы первой степени. Простейшим примером сумм Вейля является сумма первой степени 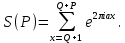 Это сумма относится к числу немногих тригонометрических сумм, которые удается не только оценить, но и непосредственно вычислить. Действительно, если 𝛼- целое, то 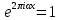 и , следовательно, и , следовательно,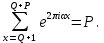 Если же 𝛼 не является целым числом, то 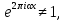 и , и ,геометрическую прогрессию, получим 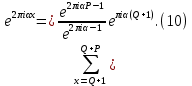 Однако обычно удобнее пользоваться не этими точными равенствами, а следующей оценкой: 1. Пусть 𝛼-произвольное действительное число Q-целое и P-натуральное. Тогда 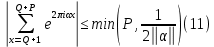 где 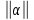 -расстояние от 𝛼 до ближайшего целого. -расстояние от 𝛼 до ближайшего целого.Доказательство. Так как обе части (11) является четными периодическими функциями 𝛼 с периодом, равным единице, то оценку (11) достаточно доказать при 0≤ 𝛼 ≤ 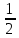 . Замечая, что на этом интервале . Замечая, что на этом интервале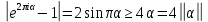 , ,при𝛼≠0 из равенства (10) получим 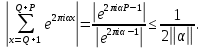 Пользуясь этой оценкой при 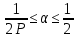 и применяя при и применяя при 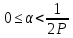 тривиальную оценку тривиальную оценку 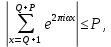 получаем утверждение леммы. Пусть 𝛼-произвольное целое и q-натуральное. Определим функцию 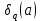 c помощью равенства 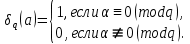 В следующей лемме устанавливается связь между этой функцией и полными рациональными суммами первой степени. Лемма 2. При любом целом а и любом натуральном q выполняется равенство 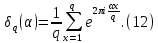 Доказательство. Если α≡0 (mod q), то 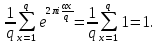 Пусть теперь α≠0 (mod q). Тогда получим 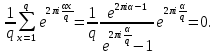 Утверждение леммы следует, очевидно, из этих равенств и определения 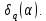 Функция 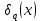 постоянно будет использоваться в дальнейшем изложении. Ее значение определяется тем, что она позволяет устанавливать связь между исследованием тригонометрических сумм и вопросом о числе решений сравнений. постоянно будет использоваться в дальнейшем изложении. Ее значение определяется тем, что она позволяет устанавливать связь между исследованием тригонометрических сумм и вопросом о числе решений сравнений.Рассмотрим, например, вопрос о числе решений сравнения 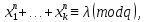 (13) (13)аналогичный упомянутому во введении вопросу о числе решений уравнения Варинге (2). Обозначим через T( 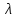 ) число решений этого сравнения, когда величины ) число решений этого сравнения, когда величины  независимо друг от друга пробегают полные системы вычетов по модулю q. Очевидно, в силу определения функции независимо друг от друга пробегают полные системы вычетов по модулю q. Очевидно, в силу определения функции 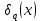 , ,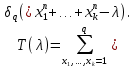 Отсюда, согласно лемме 2, следует, что 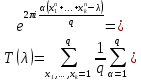 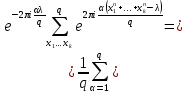 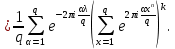 Таким образом, число решений сравнения (13) выражено через полные рациональные тригонометрические суммы 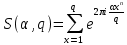 Приведем некоторые свойства функции 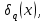 непосредственно следующие из ее определения. непосредственно следующие из ее определения.1°. Функции 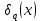 периодично. Ее период равен q. периодично. Ее период равен q.2°. Если (a , q)=1 и b- произвольное целое, то справедливы равенства 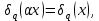 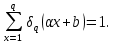 3°. При любом натуральном 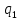 выполняется равенства выполняется равенства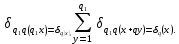 4°. Если 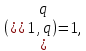 справедливо равенство справедливо равенство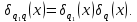 5°. При любом натуральном P, не превосходящем q, будет 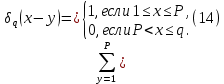 Лемма 3. Пусть q-произвольное натуральное, 1≤α 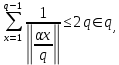 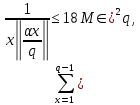 где М- наибольшее из неполных частных числа 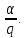 Доказательство. Пусть m- произвольное натуральное число. Пользуясь при x≥1 неравенством 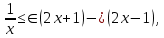 получим 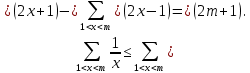 Отсюда соответственно при нечетном и при четном q cледует, что 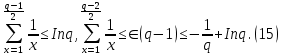 Так как функция 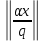 периодично с периодом q и периодично с периодом q и 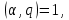 то при нечетном q согласно (15) получим то при нечетном q согласно (15) получим 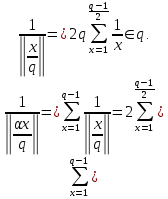 Такая же оценка получается в силу (15) и при четном q: 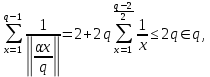 чем доказано первое утверждение леммы. чем доказано первое утверждение леммы. Для доказательства второго утверждения применим преобразование Абеля 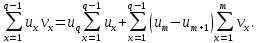 При 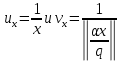 получим получим 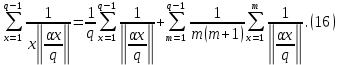 Пусть разложение числа a/q в ценную дробь имеет вид 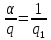 + + 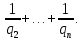 Тогда при 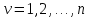 выполняются равенства выполняются равенства 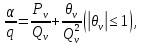 (17) (17)где 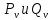 взаимно просты, взаимно просты, 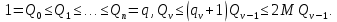 Если 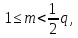 то , определяя то , определяя 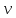 из условия из условия 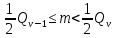 и пользуясь равенством (17), получим 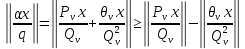 . (18) . (18)Так как при 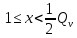 будет будет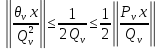 то из (18) следует, что 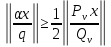 . .Но тогда, пользуясь первым неравенством леммы, получим 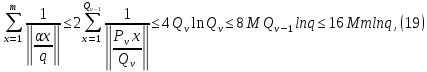 Если же 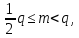 то то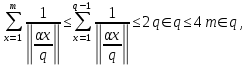 и, следовательно оценка (19) выполняется не только при 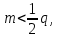 но при любом m но при любом m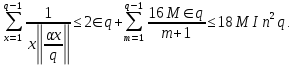 Покажем, что леммы, содержащие еще совсем небольшую информацию о тригонометрических суммах, позволяют получать нетривиальные арифметические результаты. Пусть 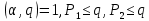 и T-число решений сравнения и T-число решений сравнения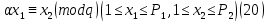 Если 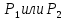 совпадает с q, то, очевидно, совпадает с q, то, очевидно,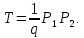 Вопрос становится сложнее, если и 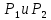 меньше чем q. В этом случае можно показать, что меньше чем q. В этом случае можно показать, что 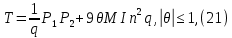 где М-наибольшее из неполных частных разложения 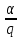 в ценную дробь. в ценную дробь.Действительно, пользуясь леммой 2, получим 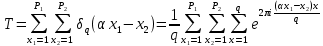 Отсюда после выделения слагаемого с x=q следует, что 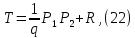 где 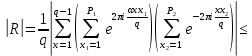 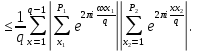 Таким образом вопрос о числе решений сравнения (20) сводится к вопросу об оценке сумм Вейля первой степени. Пользуясь леммой 1 и замечая, что 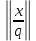 и 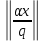 - четные периодические функции с периодом q, получим - четные периодические функции с периодом q, получим 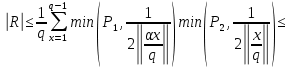 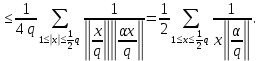 Отсюда согласно лемме 3 следует, что 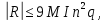 а это оценка в силу (22) равносильно равенству (21). Общие свойства полных сумм Как уже было сказано, сумма 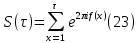 называется полной тригонометрической суммой, если при любом целом х для дробный долей функции f(x) выполняется равенство 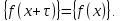 Приведем некоторые примеры полных сумм. Пусть 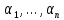 - целые и - целые и 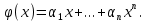 Так как, очевидно, Так как, очевидно, 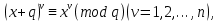 то выполняются сравнения то выполняются сравнения 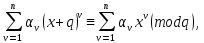 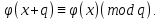 Но тогда при любом целом x 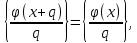 и, следовательно сумма 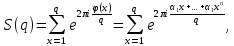 названная во введении полной рациональной суммой, будет полной тригонометрической суммой в смысле определения(23). Рассмотрим теперь тригонометрическую сумму с показательной функцией 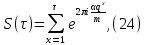 где (α,m)=1, (q,m)=1 и τ-показатель, которому q принадлежит по модулю m. Будем под где (α,m)=1, (q,m)=1 и τ-показатель, которому q принадлежит по модулю m. Будем под 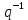 понимать решение сравнения qx≡1(mod m), при любом целом x получим понимать решение сравнения qx≡1(mod m), при любом целом x получим 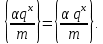 Следовательно, τ является периодом дробных долей 2∗ функции 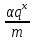 и сумма (24) будет полной тригонометрической суммой. и сумма (24) будет полной тригонометрической суммой.Приведем некоторые свойства полных сумм, непосредственно следующие из определения. 1°. Величина полной тригонометрической суммы (23) не изменится, если переменная суммирования вместе интервала 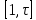 будет пробегать любую полную систему вычетов по модулю τ. будет пробегать любую полную систему вычетов по модулю τ.Действительно, так как 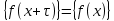 , то при x ≡ y (mod τ) выполняется равенство , то при x ≡ y (mod τ) выполняется равенство 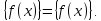 Ну тогда 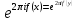 И совокупность слагаемых в сумме (23) не будет зависеть от того, образующие по модулю 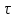 полную систему вычетов, пробегает переменная суммирования. полную систему вычетов, пробегает переменная суммирования.2 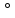 . Если ( . Если (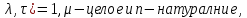 то для полных сумм выполняются равенства то для полных сумм выполняются равенства 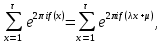 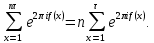 Первое из этих равенств является частным случаем свойства 1 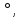 так как при ( так как при (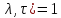 линейная функция линейная функция 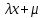 одновременно с х пробегает полную систему вычетов по модулю одновременно с х пробегает полную систему вычетов по модулю 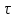 . .3 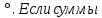 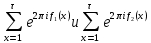 являются полными, то полной будет и сумма 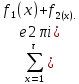 Действительно, из полноты сумм (27) следует, что дробные доли функций 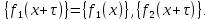 Но тогда { 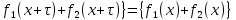 И сумма (28) будет полной тригонометрической суммой. Теорема 1 (формула умножения). Пусть при целых {f (х) }= { 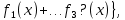 Где дробные доли функсий 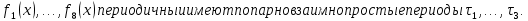 Тогда справедливо равенство 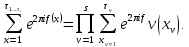 Доказательство. Так как, согласно условию, 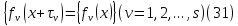 и в силу (29) 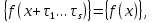 то все тригонометрические суммы в равенстве (30) являются полными. Пусть величины 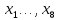 независимо друг от друга пробегают полные системы вычетов соответственно по модулям независимо друг от друга пробегают полные системы вычетов соответственно по модулям 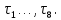 При этом, так как При этом, так как 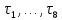 попарно взаимно просты, сумма попарно взаимно просты, сумма 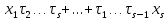 будет пробегать полную систему вычетов по модулю 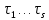 и следовательно, и следовательно,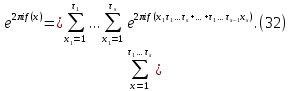 Так как в силу (29) и (31) 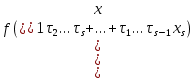 то равенство (23) можно переписать в виде 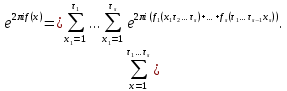 Отсюда, пользуясь свойством (25), получаем формулу умножения:  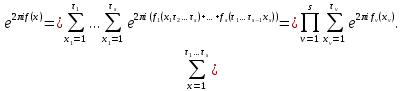 Формула умножения в ряде случаев существенно упрощает исследование полных сумм. Покажем этот на примере полных рациональных сумм. Пусть 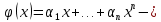 произвольный целочисленный полином произвольный целочисленный полином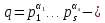 каноническое разложение q на простые сомножители и числа каноническое разложение q на простые сомножители и числа 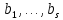 выбраны так , чтобы выполнялось сравнение выбраны так , чтобы выполнялось сравнение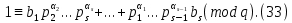 Тогда для полных рациональных сумм справедливо равенство 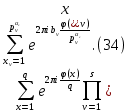 Действительно, так как 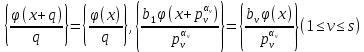 и в силу (33) и в силу (33)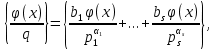 то применяя теорему 1, получаем равенство (34). Формула умножения (34) сводит исследование полных рациональных сумм с произвольным знаменателем q к исследованию более простых сумм со знаменателем, равным степени простого числа. В качестве другого примера на формулу умножения докажем равенство 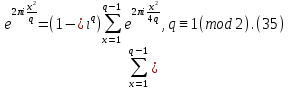 Которое понадобится в дальнейшем при исследовании сумм Гаусса. Рассмотрим сумму 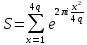 Выделим слагаемые, с х, кратным q, и объединим остальные слагаемые в четыре группы: 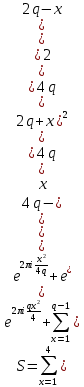 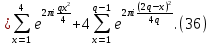 С другой стороны, согласно формуле умножения 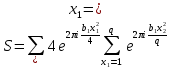 где 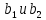 удовлетворяют сравнению удовлетворяют сравнению 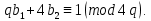 Так как это сравнение выполняется при Так как это сравнение выполняется при 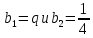 (1− (1−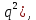 то после выделение слагаемого то после выделение слагаемого 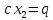 и замены и замены 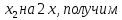 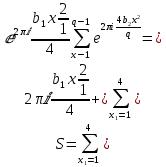 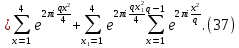 Теперь, замечая, что 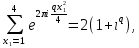 Из (36) и (37) получаем равенство (35): 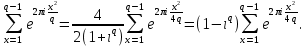 Рассмотрим теперь некоторый класс тригонометрических сумм, нетривиальные оценки которых можно легко получить путем сведения задачи к оценке полных сумм. Пусть дробные доли функции f(x) периодичны, их наименьший период равен τ, 1≤P<τ и Q- произвольное целое. Тогда сумма 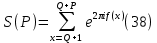 называется неполной тригонометрической суммой. Теорема 2. Для всякой неполной тригонометрической суммы S(P), определенной равенством (38), выполняется оценка 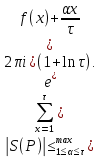 Доказательство. Из свойства (14) функции 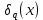 следует, что при P≤𝜏 следует, что при P≤𝜏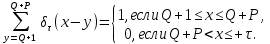 Применяя этот разрывный множитель и пользуясь леммой 2, получим 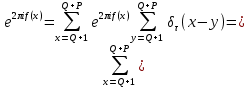 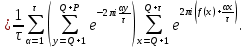 Так как дробные доли функций f(x) и 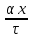 имеют период 𝜏, то согласно (28) последнаяя сумма в этом равенстве является полной и, следовательно, имеют период 𝜏, то согласно (28) последнаяя сумма в этом равенстве является полной и, следовательно, 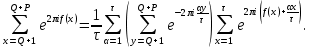 Отсюда, пользуясь леммами 1 и 3 , получаем утверждение теоремы: 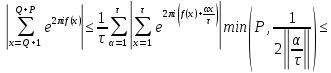 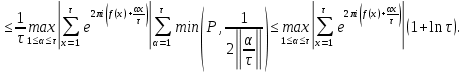 Суммы Гаусса Суммой Гаусса называется полная рациональная тригонометрическая сумма второй степени 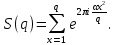 где q- произвольное натуральное число и (𝛼, q)=1. Суммы Гаусса, так же как и рассмотренные и первом параграфе суммы первой степени, можно точно вычислить. Рассмотрим сперва сравнительно простой вопрос о вычислении модуля таких сумм. Теорема 3. Для модуля суммы Гаусса выполняется равенство 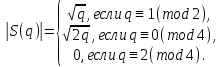 Доказательство. Обозначим через 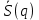 сумму, сопряженную сумме S(q). Тогда получим сумму, сопряженную сумме S(q). Тогда получим 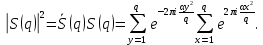 Воспользуемся вторым свойством полных сумм и заменим во внутренней сумме x на x+ y. Тогда, после перемены порядка суммирования, получим 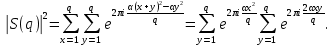 Отсюда согласно лемме 2 следует, что 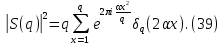 Так как по условию 𝛼 и y взаимно просты, то при нечетном q в первой части этого равенства отлично от нуля только то слагаемого, которое получается при x=q, и, следовательно, 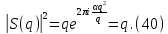 Если же q четно, то в сумме (39) отличны от нуля два слагаемых, которые получается при 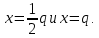 Поэтому, замечая что при четном q из (𝛼,q)=1 следует нечетность а получим Поэтому, замечая что при четном q из (𝛼,q)=1 следует нечетность а получим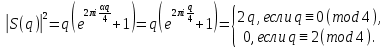 Отсюда и из равенства (40) следует утверждение теоремы. Заметим, что в случае нечетного q утверждение теоремы 3 справедливо и для сумм общего вида. Действительно, покажем, что при 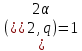 выполняется равенство выполняется равенство 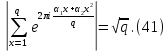 Выберем b так, чтобы выполнялось сравнение 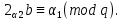 Тогда очевидно, Тогда очевидно, 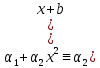 и, следовательно, 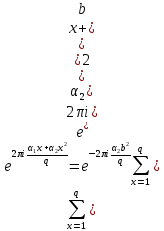 Отсюда получаем равенство (41): 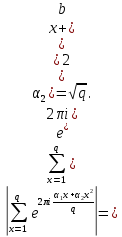 Рассмотрим простейшие свойства сумм Гаусса. Будем предполагать, что q=p, где p>2-простое число. Легко показать, что при 𝛼≡0(mod p) справедливо равенство 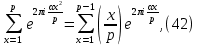 где 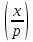 - символ Лежандра. Действительно, если x изменяется от 1 до p-1, то - символ Лежандра. Действительно, если x изменяется от 1 до p-1, то 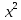 дважды пробегает значения квадратичных вычетов по модулю p, и так как дважды пробегает значения квадратичных вычетов по модулю p, и так как 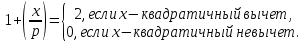 то 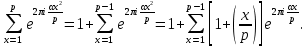 Отсюда, замечая, что согласно лемме 2 при 𝛼≢0(modp) 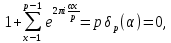 получаем равенство (42). Покажем теперь, что при 𝛼≢0(modp) 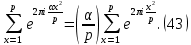 Действительно, умножая равенство (42) на Действительно, умножая равенство (42) на 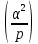 =1 и замечая, что 𝛼x пробегает приведенную систему вычетов одновременно с x, получим =1 и замечая, что 𝛼x пробегает приведенную систему вычетов одновременно с x, получим 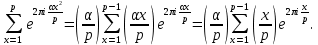 Отсюда, так как в силу (42) 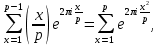 следует равенство (43). Покажем еще, что зная модуль суммы Гаусса, легко вычислить ее значение с точностью до знака. Действительно, пусть 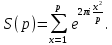 Тогда, пользуясь равенством (43), получим 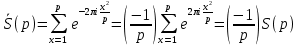 Отсюда после умножения на 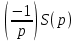 следует, что следует, что 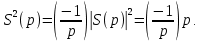 Теперь, так как 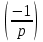 принимает значение 1 при p≡1(mod 4) и значение -1 при p≡3(mod 4), получаем принимает значение 1 при p≡1(mod 4) и значение -1 при p≡3(mod 4), получаем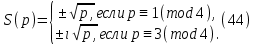 Вопрос о том, какой знак следует выбрать в этих равенствах, более сложен. Его решение было найдено Гауссом. Ниже приведено сравнительно простое доказательство теоремы Гаусса, предложенное в работе  Теорема 4. При любом нечетном простом p выполняется равенства 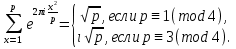 Доказательство. Покажем сначала, что 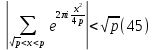 Действительно применим преобразования Абеля 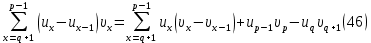 при 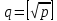 и и 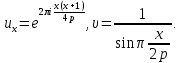 Так как, очевидно, 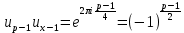 и 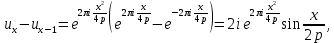 то из (46) следует, что 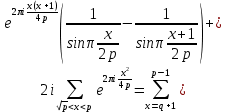 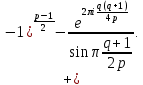 Но тогда, замечая, что при 1≤ x≤ p−1 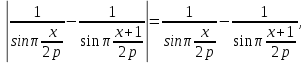 получим 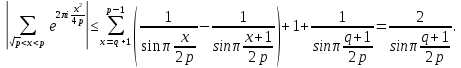 Отсюда, так как 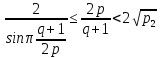 следует оценка (45). Теперь, замечая, что 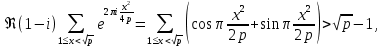 и пользуясь оценкой (45), получим и пользуясь оценкой (45), получим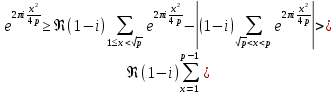 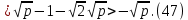 Пусть p≡1(mod 4). Тогда согласно (44), 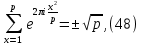 т.е. эта сумма является действительным числом, и , следовательно, 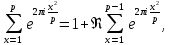 Так как , согласно (35) при p≡1(mod 4) 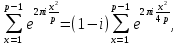 то, пользуясь оценкой (47), получим 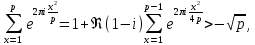 чем в силу (48) доказано первое утверждение теоремы. Если p≡3(mod 4), то и согласно (35) и (44) 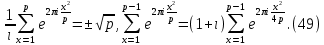 и, как и выше , получим 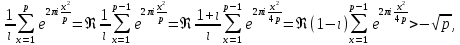 чем в силу первого из равенств (49) теорема доказана полностью. Заметим, что утверждение теоремы 4 можно записать с помощью одного равенств, не выделяя особо случаи p≡1(mod 4) и p≡3(mod 4): 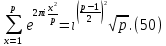 Отсюда в силу (43) при любом α≢0(mod p) получаем 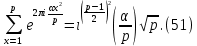 Равенство (50) доказано в предположении, что p-простое нечетное число. Покажем, что такое же равенство справедливо и для сумм Гаусса с произвольным нечетным знаменателем q: 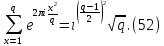 Рассмотрим сначала суммы вида 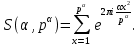 где 𝛼-натуральное, p-нечетное простое и 𝛼 взаимно простое с p. Пользуясь индукцией по 𝛼, легко показать, что 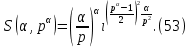 Действительно, при 𝛼=1 это равенство совпадает с равенством (51). При 𝛼=2 оно принимает вид 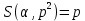 и получается с помощью замены переменной суммирования: и получается с помощью замены переменной суммирования: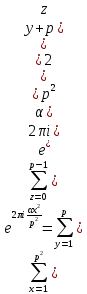 Пусть равенство (53) доказано для некоторого 𝛼≥2 и всех меньших значений 𝛼. Докажем его для 𝛼+1. Очевидно 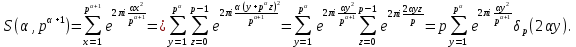 Замечая, что в последний сумме отличны от нуля только слагаемые с y, кратным p, и что 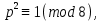 получим получим 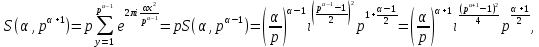 чем равенство (53) доказано полностью. Пусть теперь q>1- произвольное нечетное число. Запишем каноническое разложение q в виде 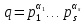 и определим и определим 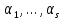 из сравнения из сравнения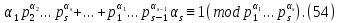 Будем считать, что в произведении 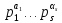 нечетные степени простых стоит на первых r местах. Так как равенство (53) можно записать в виде нечетные степени простых стоит на первых r местах. Так как равенство (53) можно записать в виде 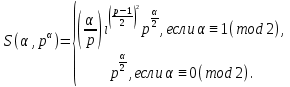 то, пользуясь формулой умножения (34), получим 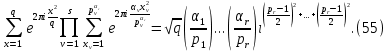 Из определения (54) следует, что 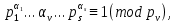 и, так как 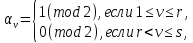 то очевидно, при 1<v≤r 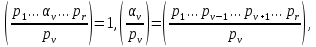 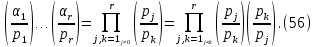 Определим величины 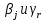 равенствами равенствами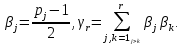 Тогда, пользуясь законом взаимности квадратичных вычетов в форме 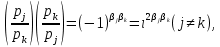 из (55) и (56) получим 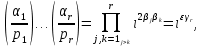 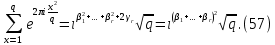 Так как, очевидно, 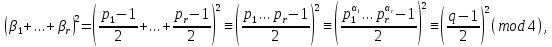 то из (57) следует, что для всякое нечетного q выполняется равенство (52): 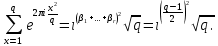 Точное значение сумм Гаусса известно и для произвольное четного q. Если q≡2(mod 4), то согласно теорема 3 сумма Гаусса обращается в нуль. При q≡0(mod 4) можно показать, что 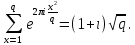 Таким образом полное описание величины сумм Гаусса дается равенствами 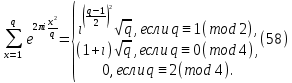 Простейшие полные суммы Естественным обобщением сумм Гаусса являются полные рациональные суммы вида 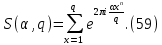 где α и q взаимно просты и n≥2. В отличие от сумм Гаусса (n=2) при n  для сумм (59) уже не удается получить явное выражение, но для них легко установить оценки , порядок которых не допускает дальнейшего улучшения. Совсем просто получается оценка для сумм (59) уже не удается получить явное выражение, но для них легко установить оценки , порядок которых не допускает дальнейшего улучшения. Совсем просто получается оценка 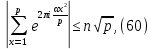 где p-простое число . Действительно, пусть, соответственно, T(b) и T- число решений сравнений 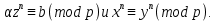 Пользуясь свойствами двучленных сравнений, получим Пользуясь свойствами двучленных сравнений, получим T(b)≤d, T=1+d(p-1). (61) где d=(n, p-1). С другой стороны, согласно лемме 2, 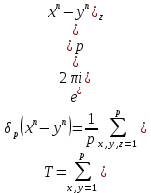 Следовательно, в силу (61), 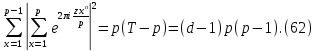 Так как согласно (25) при 1≤z≤p-1 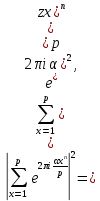 то, проводя суммирование по z, получим, 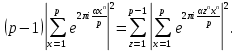 Объединим здесь слагаемые с 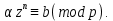 Тогда, пользуясь оценкой (61) и равенством (62), получим Тогда, пользуясь оценкой (61) и равенством (62), получим 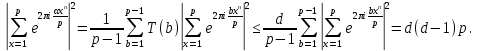 1 2 |
