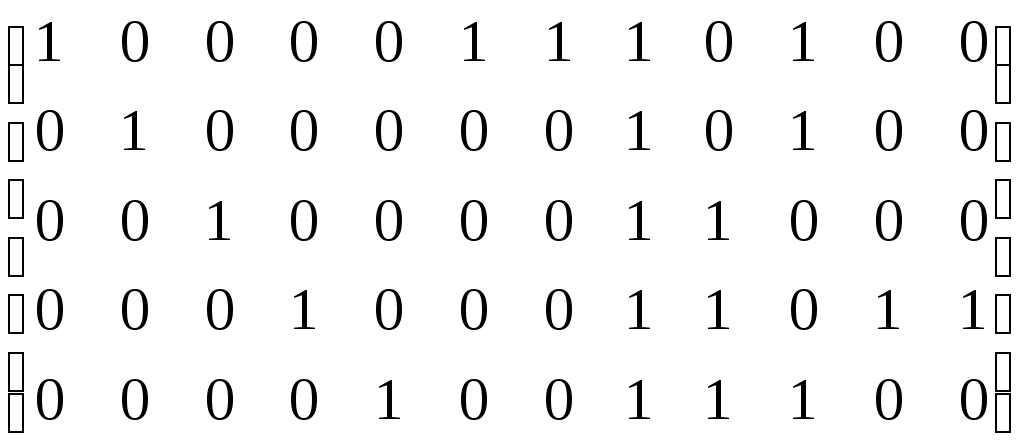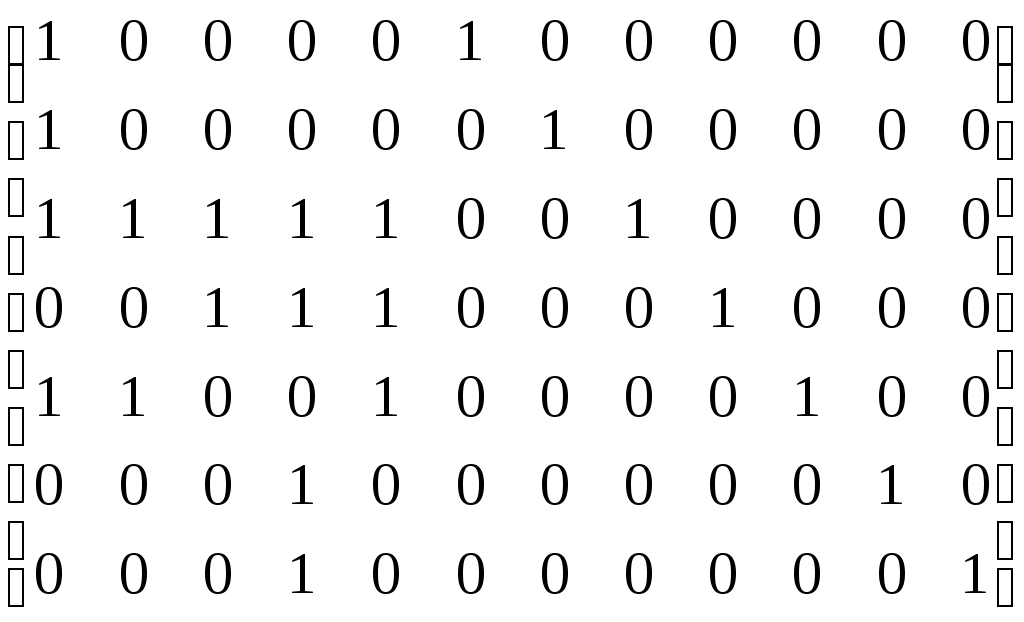Типовые расчеты по дискретной математике
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
1 2
R.
З  адание 1. адание 1.Докажите тождества, используя только определения операций над множествами. 1) 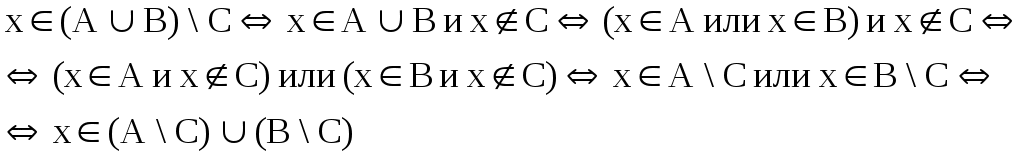 2) 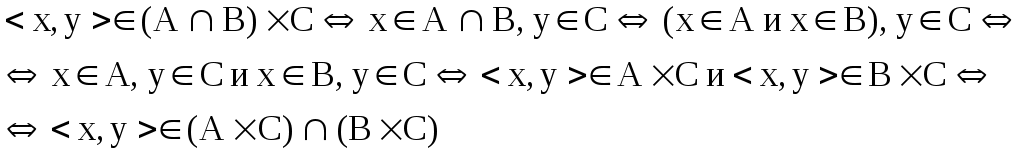   Задание 2. Докажите утверждение. [a,b] |
| x | y | | | | |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
2)
| x | y | z | | | | | | |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |


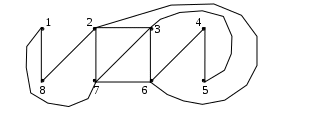
Задание 12.
Проверьте двумя способами, будут ли эквивалентны следующие формулы
а) составлением таблиц истинности
б) приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований.
а)
| x | y | z | yz | | x | x | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Так как столбцы
б)
Так как СДНФ двух формул отличаются, то формулы неэквивалентны.


Задание 13.
С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкина.
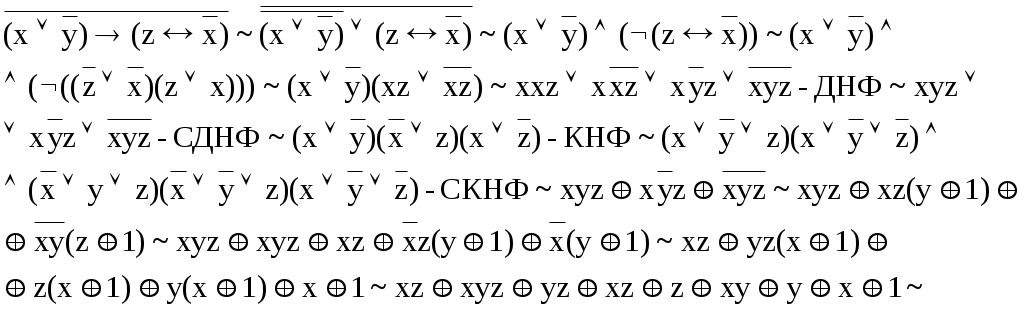


Задание 14.
Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции
а) методом Квайна б) с помощью карт Карно
Каким классам Поста принадлежит эта функция?
а)
| x | y | z | |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
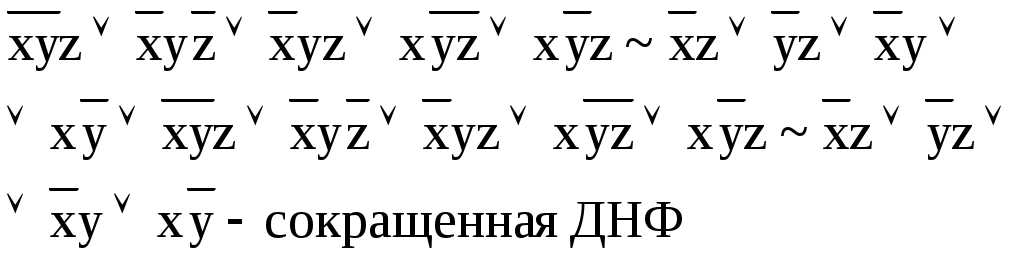
| | | | | | |
| | * | | * | | |
| | * | | | | * |
| | | * | * | | |
| | | | | * | * |
 тупиковые и минимальные ДНФ.
тупиковые и минимальные ДНФ. б)
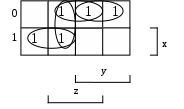
 тупиковые и минимальные ДНФ.
тупиковые и минимальные ДНФ. 1)
2)
3)
4
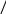 )
)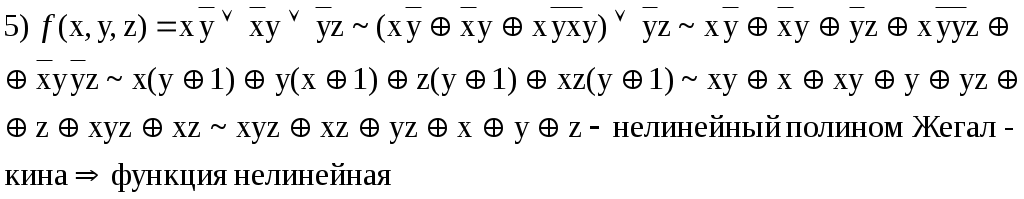


Задание 15.
С помощью карт Карно найдите сокращенную, все тупиковые и минимальные ДНФ и КНФ булевой функции
(1100 1011 1111 1011)
| x | y | z | v | |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
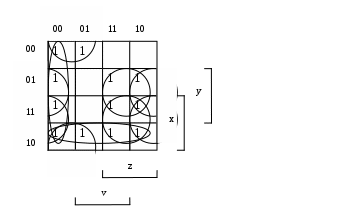
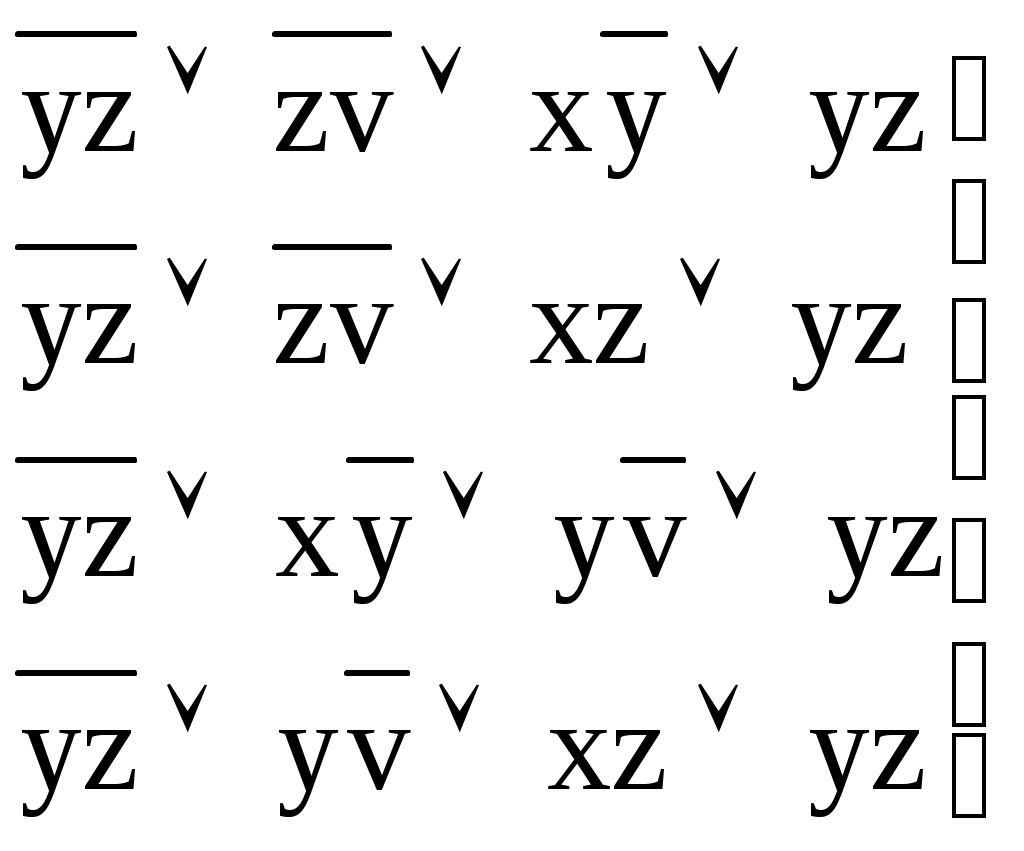 тупиковые и минимальные ДНФ.
тупиковые и минимальные ДНФ.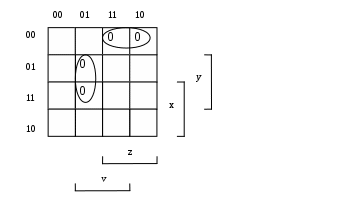


Задание 16.
Является ли полной система функций
1 2

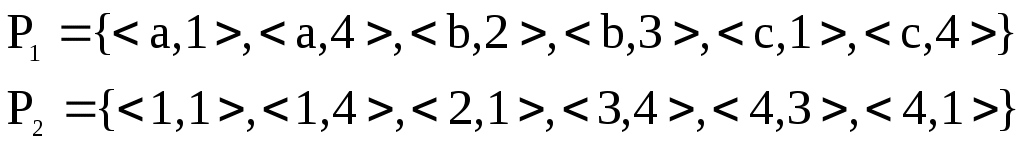
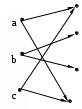
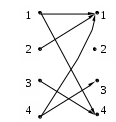
 [
[
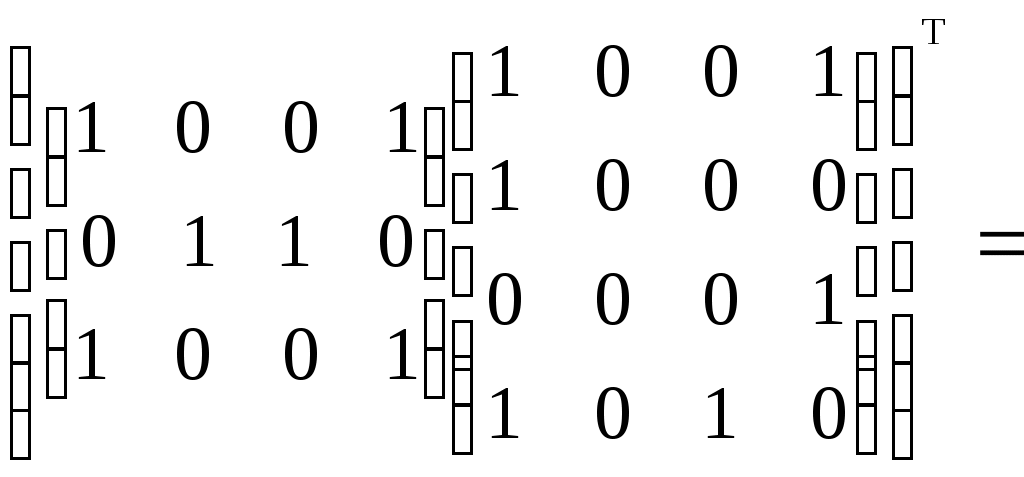
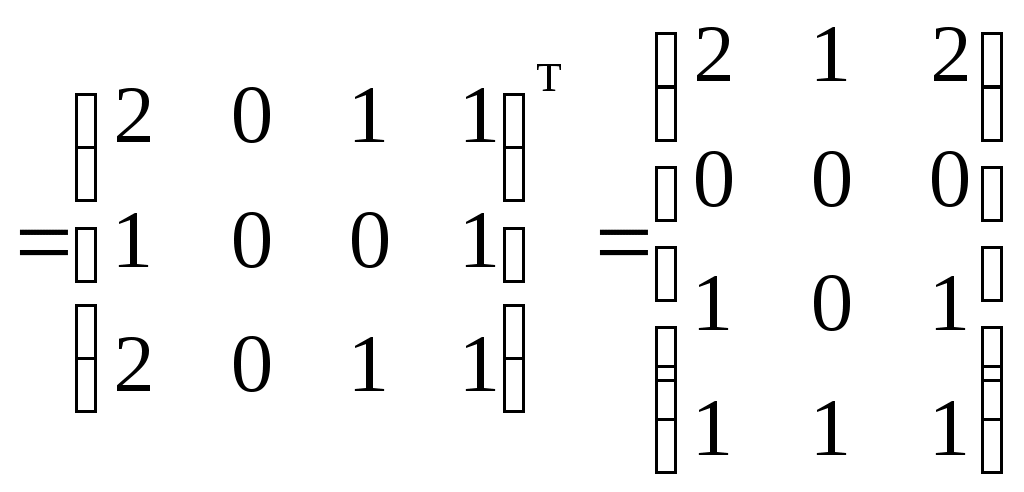
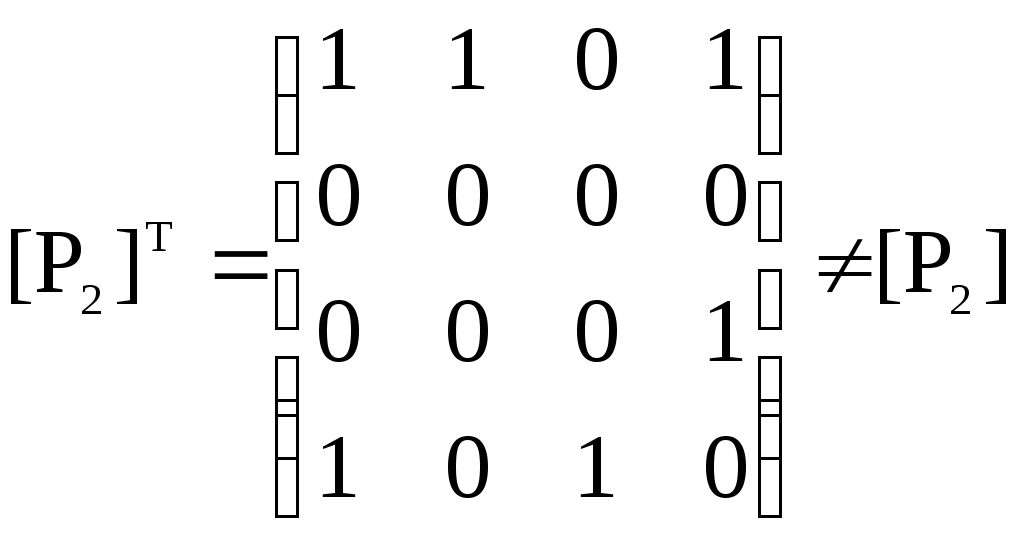 –
–  )
)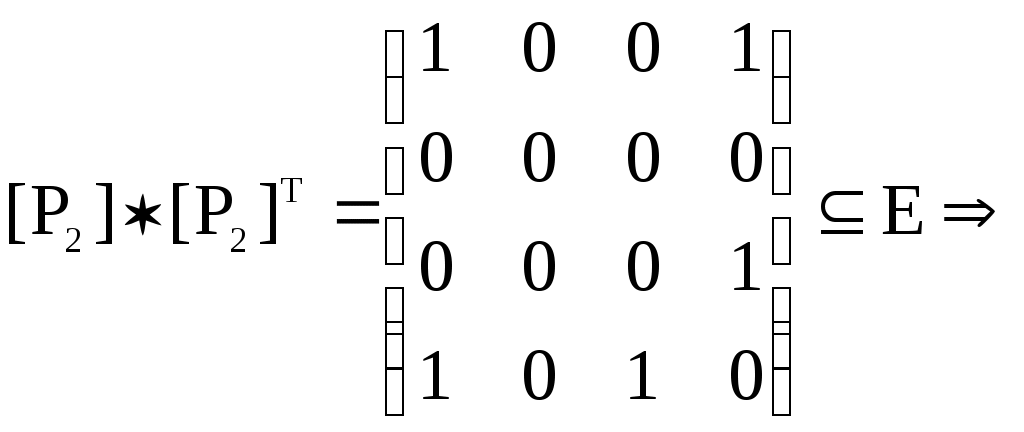
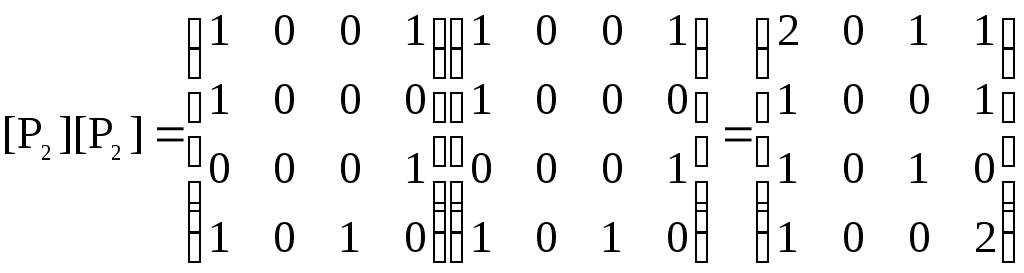
 /
/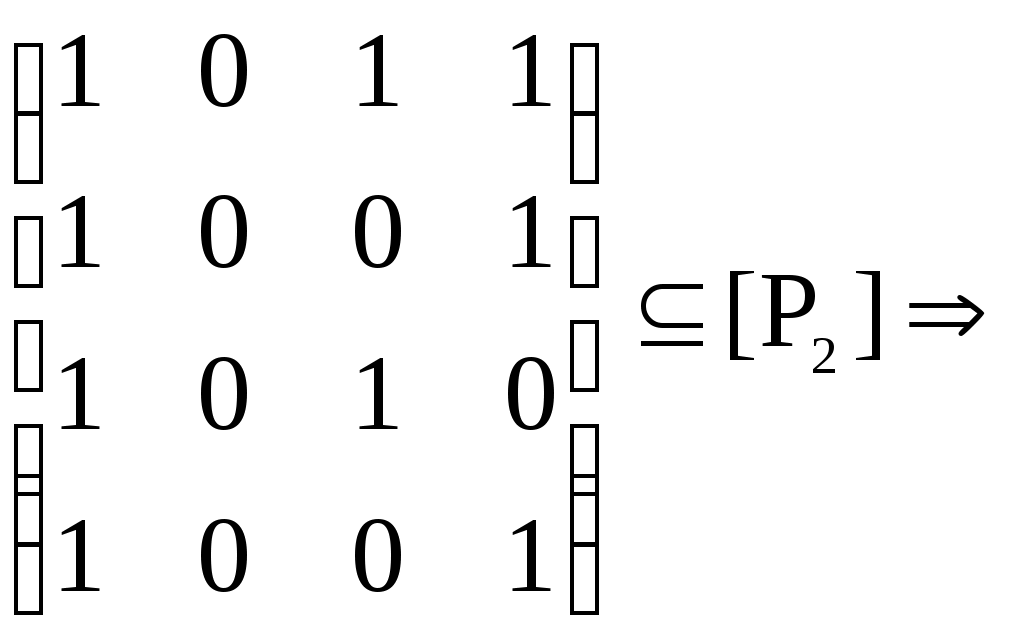 отношение
отношение 
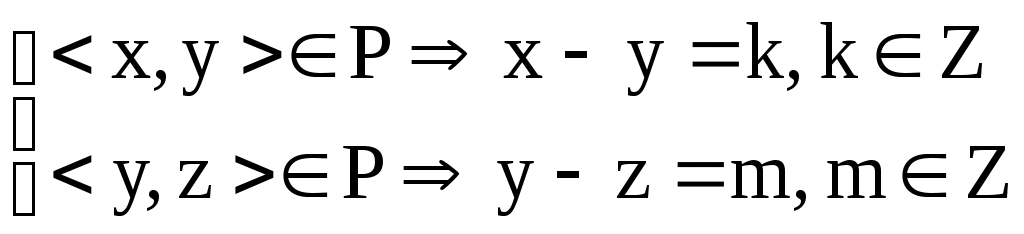 , тогда x–(z+m)=k
, тогда x–(z+m)=k 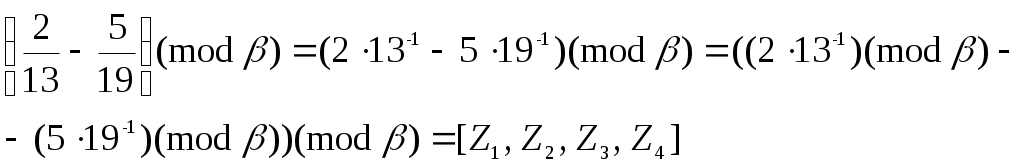






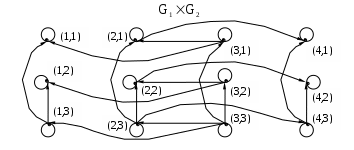
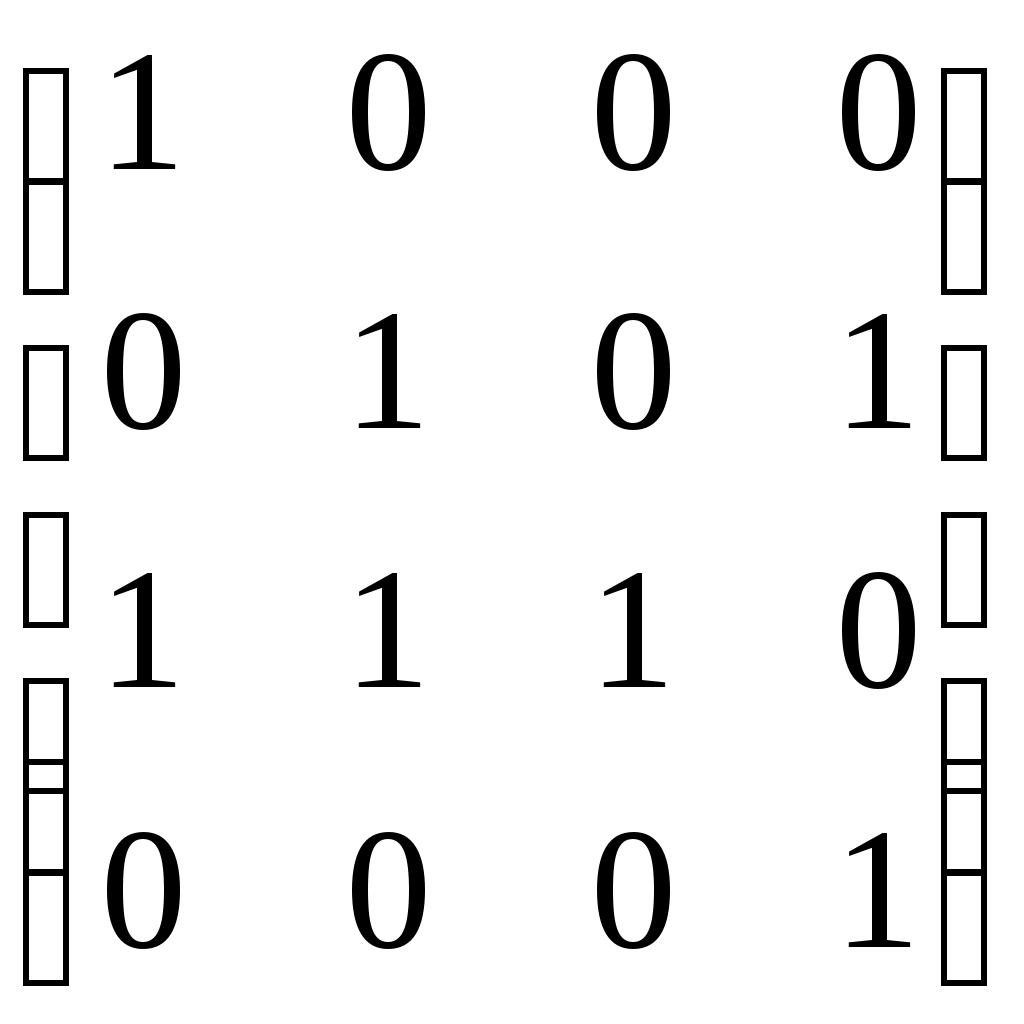



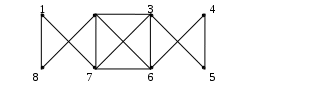
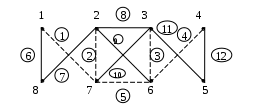
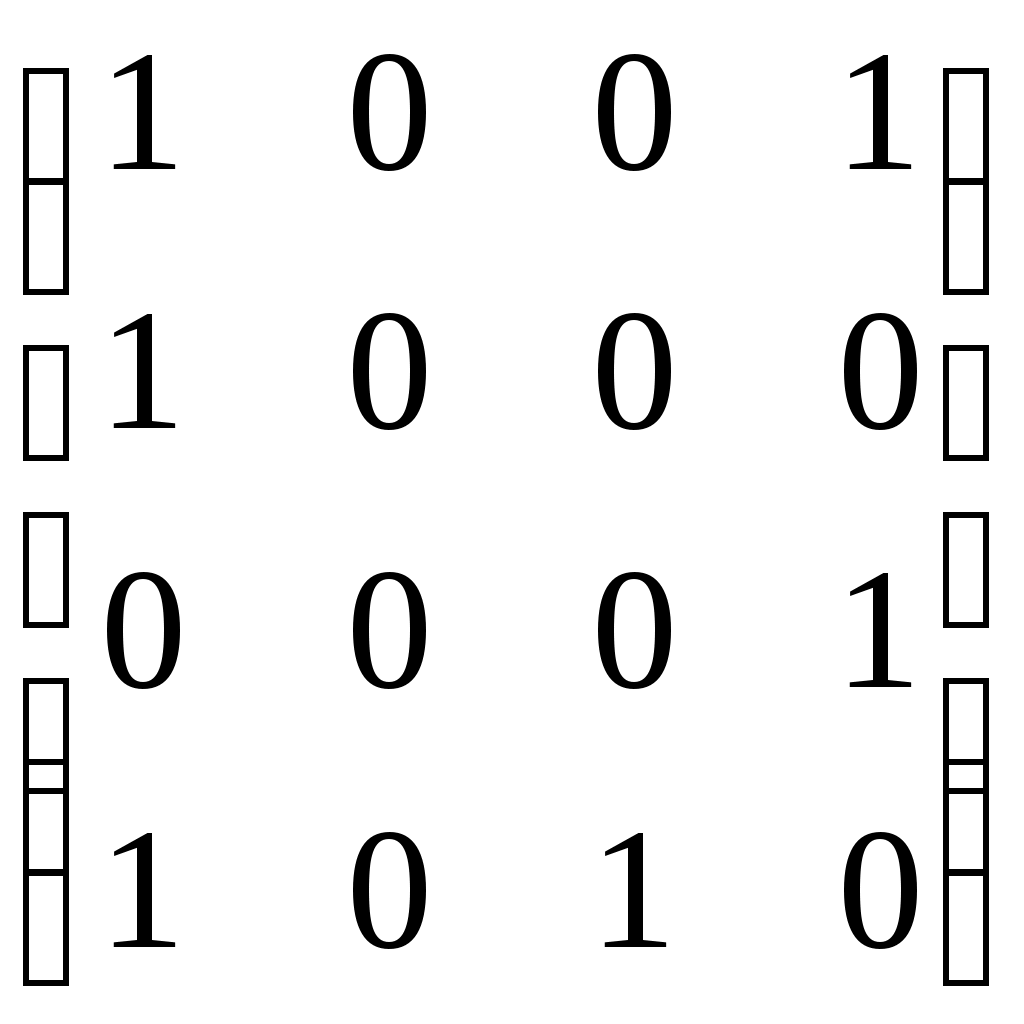
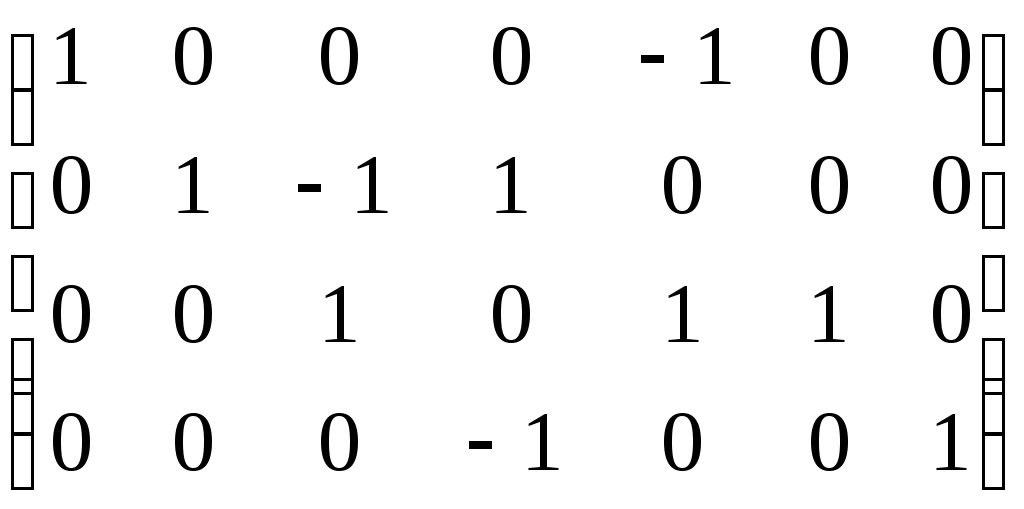 – матрица инцидентности
– матрица инцидентности 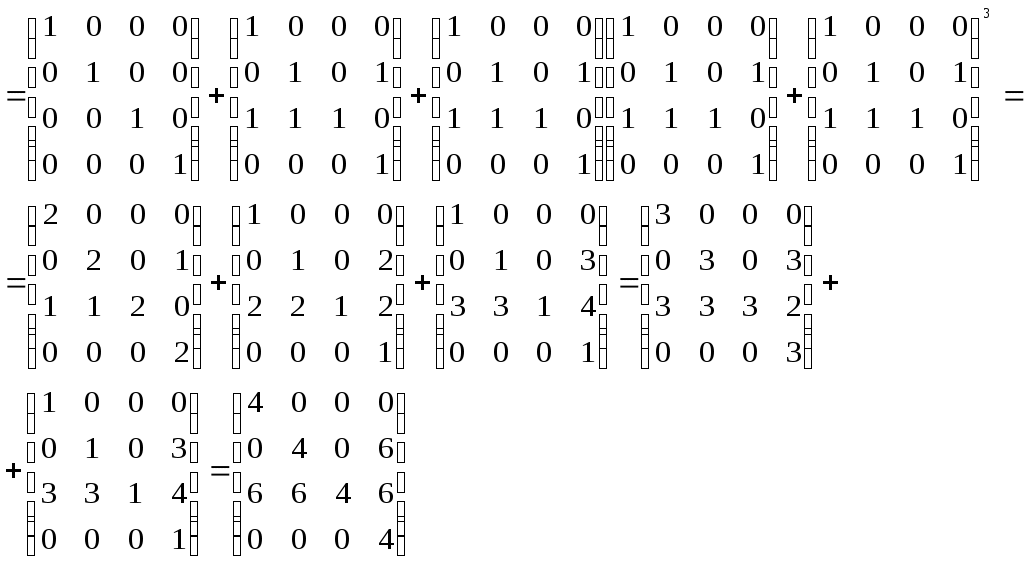
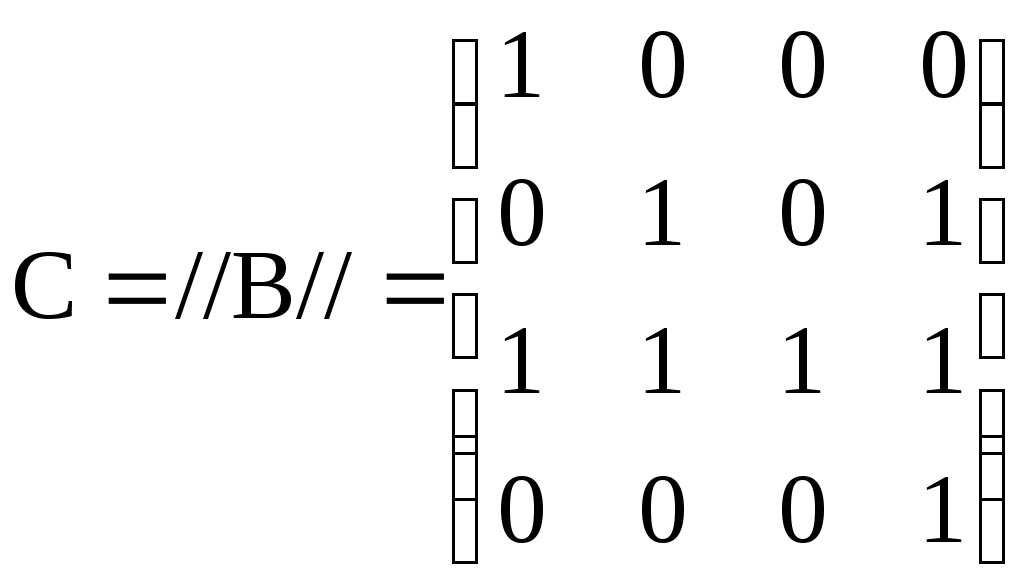
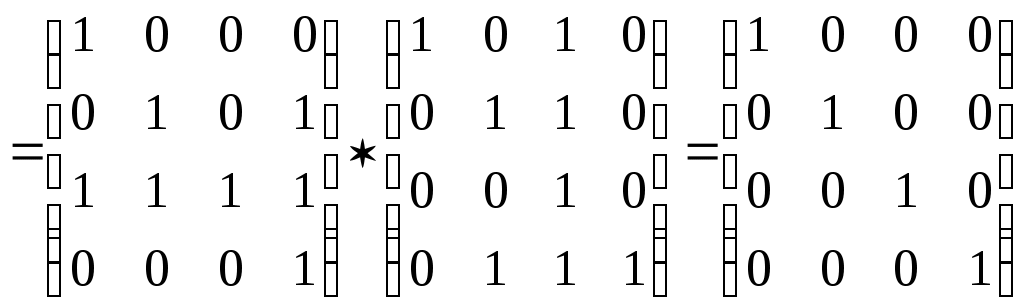 – матрица сильных компонент.
– матрица сильных компонент.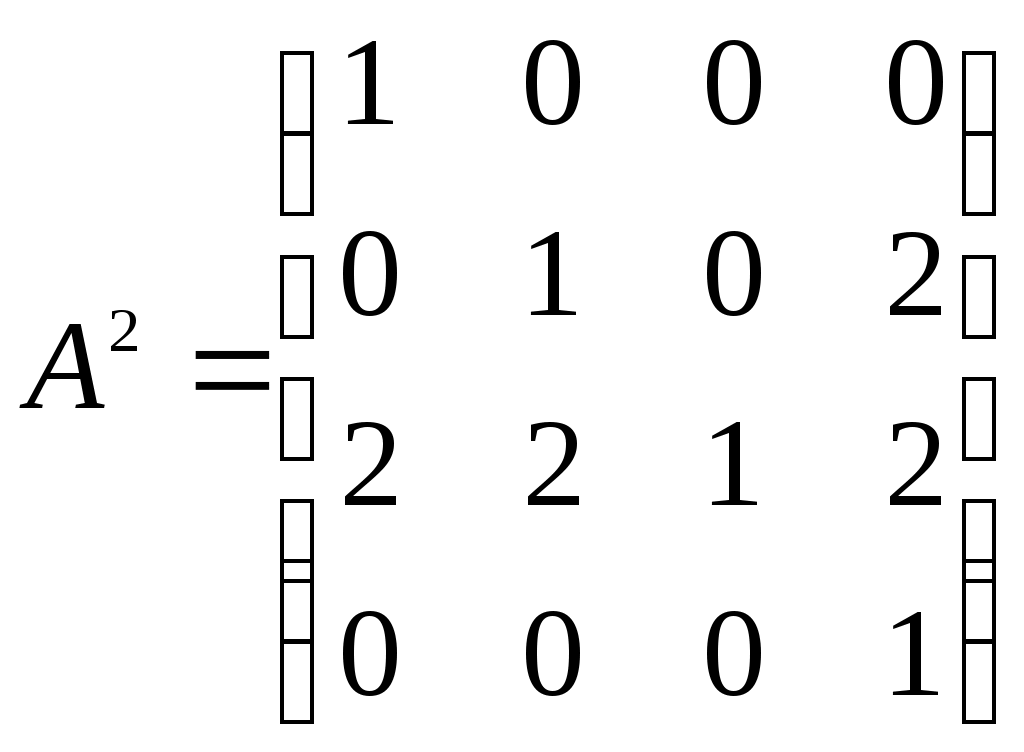 – матрица маршрутов длины 2.
– матрица маршрутов длины 2.