билеты. У Определение выпуклого многоугольника. Сумма углов выпуклого многоугольника (доказать)
 Скачать 2.3 Mb. Скачать 2.3 Mb.
|
|
ув1. Определение выпуклого многоугольника. Сумма углов выпуклого многоугольника (доказать).   2. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма. Ответ: h=6 см, S= 84 см2. Билет № 2. 1. Определение параллелограмма. Признаки параллелограмма (один по выбору доказать).      2. Периметр параллелограмма ABCD равен 60 см. Биссектриса острого угла А делит сторону ВС на равные части. Точка Е – пересечение биссектрисы и стороны ВС. АЕ= 8 см. Найти периметр треугольника АВЕ. Ответ: Р = 28 см. (АВ = ВЕ =ЕС = 30/3 = 10 см, Р =10+10 + 8 =28 см) Билет №3. 1. Определения четырехугольника, параллелограмма. Доказать свойство диагоналей параллелограмма.     2. Основание равнобедренного треугольника равно 26 см., угол при основании равен 60°. Найти периметр треугольника. Ответ: Р =26 + 26 + 26 =78 см. Билет №4. 1. Определение трапеции, её виды. Вывод формулы площади трапеции.     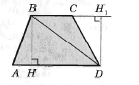 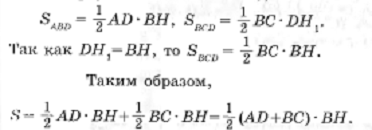  2. Найдите углы параллелограмма, если один из её углов равен 65°. Ответ: 650, 1150, 650, 1150. Билет №5. 1.Определение прямоугольника. Доказать свойство его диагоналей.   2.Длины двух сторон параллелограмма пропорциональны числам 7 и 3. Одна из них на 12 см. больше другой. Найти периметр параллелограмма. Ответ: Р = 60 см. (7х – 3х =12, х =3) Билет № 6. 1. Определение ромба. Доказать свойство его диагоналей. 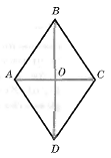    2. Найти боковую сторону и площадь равнобедренного треугольника, если основание равно 18 см., а угол, противолежащий основанию, равен 120°. Ответ: 6 Билет № 7. 1. Определение средней линии треугольника. Доказать свойство средней линии треугольника.  2. Найти высоту телеграфного столба, если его тень равна 6,3 м, а тень дерева, стоящего около него равна 2,1 м. Высота дерева равна 1,7 м. Ответ: 5,4 м (составить пропорцию Билет № 8. 1. Определение квадрата. Свойства квадрата. Площадь квадрата.   2. Диагонали ромба 15 см. и 36 см. Найти площадь ромба. Ответ: S = (15 + 36) : 2 = 270 см2. Билет № 9. 1. Определение прямоугольного треугольника. Доказательство теоремы Пифагора.  2. Найти площадь трапеции, если её меньшее основание ВС=12 см., АВ=СD, угол D = 45°, высота трапеции равна 8 см. Ответ: S = 160 см2. (AD = 12 + 8*2 =28, S = Билет № 10. 1. Определение подобных треугольников. Признаки подобия треугольников (доказать один по выбору).    2. Стороны АВ и ВС треугольника АВС равны соответственно 16 см. и 22 см., а высота, проведённая к стороне АВ, равна 11 см. Найти высоту, проведённую к стороне ВС. Ответ: h =8 см. (S = Билет № 11. 1. Определение угла, вписанного в окружность. Свойства углов, вписанных в окружность.     2. Найти площадь трапеции ABCD с основаниями АВ и СD, если угол D=30°, АВ=2см, CD=10 см, AD=8 см. Ответ: S = 24 см2 . (S = Билет № 12. 1. Формулы площадей многоугольников. Центральный угол. S = a2 S =а*b S  = а*h = а*hS = S = S = 2. Найти диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь равна 27 см². Ответ: 6 см и 9 см. (х*1,5х2 =27) Билет № 13. 1. Касательная к окружности. Вписанная и описанная окружности.     2. Стороны треугольника равны 6 см, 8 см, 10см. Периметр подобного ему треугольника равен 48 см. Определить стороны и площадь второго треугольника. Ответ: 12 см, 16 см, 20 см, S = 8 Билет № 14. 1. Определение sin, cos, tg. Значение синуса, косинуса и тангенса углов 30°, 45°, 60°.  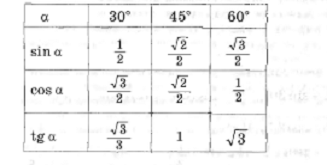 2. Вписанный угол на 21° меньше центрального угла, опирающегося на ту же дугу. Найти градусные меры этих углов. Ответ: 210, 420. (2х –х = 21, х = 21, то 2х = 42) Билет № 15. 1. Сформулируйте и докажите теорему Пифагора.  2. Хорды АВ и СD пересекаются в точке Е. Найти ED, если АЕ=16 см, ВЕ=9 см, СЕ=ЕD. Ответ: Билет № 16. 1. Определение подобных треугольников. Доказать теорему об отношении площадей подобных треугольников.    2. Найти площадь трапеции ABCD с основаниями АВ и СD, если угол D=30°, АВ=2см, CD=10 см, AD=8 см. Ответ: S= Билет № 17. 1. Осевая и центральная симметрия. Приведите примеры фигур, обладающих осевой симметрией, центральной симметрией. Постройте отрезок, симметричный отрезку АВ относительно прямой а.     2. Найти диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь равна 27 см². Ответ: 6 см и 9 см. (по формуле площади ромба через диагонали составить уравнение) Билет № 18. 1. Понятие площади многоугольника. Свойства площадей многоугольников.    2. Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если одна сторона на 3 см больше другой. Ответ: 10,5 см и 13,5 см. Билет № 19. 1. Сформулировать и доказать теорему о площади треугольника. Следствия из теоремы.   2. Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен 120°. Ответ: 6 сторон |
