|
|
Свойство вписанного четырехугольника
Технологические карты уроков по учебнику Л. С. Атанасяна
ГЛАВА VIII. ОКРУЖНОСТЬ
Урок 62. Тема: СВОЙСТВО ВПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА
Цель деятельности учителя
|
Создать условия для рассмотрения свойства вписанного четырехугольника и показать его применение при решении задач
|
Термины и понятия
|
Описанная около четырехугольника окружность, вписанный четырехугольник
|
Планируемые результаты
|
Предметные умения
|
Универсальные учебные действия
|
Владеют базовым понятийным аппаратом по основным разделам содержания
|
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.
Коммуникативные: формулируют, аргументируют и отстаивают свое мнение.
Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач
|
Организация пространства
|
Формы работы
|
Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г)
|
Образовательные
ресурсы
|
• Учебник
|
I этап. Актуализация опорных знаний учащихся
|
Цель деятельности
|
Совместная деятельность
|
Проверить домашнее задание
|
(Ф) К доске вызвать двоих учеников и проверить выполнение домашнего задания.
№ 707.
Решение:

В ∆АВС ∠A = ∠C = (180° - 120°) : 2 = 30°. Тогда ∪BC = 60° => ∠BOC = 60° => ∆ОВС - равносторонний => ОВ = ОС = r = 8 см => диаметр равен 16 см.
Ответ: 16 см.
№ 711.
Решение:
Центр описанной около треугольника окружности совпадает с точкой пересечения его серединных перпендикуляров, а радиус окружности равен расстоянию от центра окружности до любой из вершин треугольника.
В прямоугольном треугольнике центр описанной около него окружности совпадает с серединой гипотенузы, а радиус равен половине гипотенузы
|
II этап. Решение задач по готовым чертежам
|
Цель деятельности
|
Совместная деятельность
|
Повторить изученный материал и подготовить учащихся к восприятию новой темы
|
(Ф)

Найти: ∠B.

Дано: АВ : ВС = 1 : 2; АС = 5√5.
Доказать: ABCD - прямоугольник.
Найти: АВ, ВС.

Дано: MN = NK = 4.
Найти: OK.

Дано: ∆АВС - равносторонний. OK = 3
Найти: АВ.

Дано: ∆АВС – равносторонний.
Найти: АВ.

Найти: DC.

Найти: углы четырехугольника ABCD.
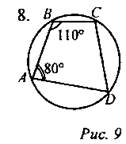
Найти: ∠C, ∠D.

Найти: ∠A + ∠C.
Ответы: 

|
III этап. Изучение нового материала
|
Цель деятельности
|
Совместная деятельность
|
Рассмотреть свойство вписанного четырехугольника
|
(Ф). 1. Объяснить, что около четырехугольника не всегда можно описать окружность, на примерах ромба, параллелограмма, не являющихся квадратом и прямоугольником соответственно.
2. Для доказательства теоремы о свойстве вписанного четырехугольника учащимся можно предложить самостоятельно решить задачу с последующим обсуждением.
Задача: Докажите, что в любом вписанном четырехугольнике сумма противоположных углов равна 180°.
3. Для доказательства утверждения, обратного свойству вписанного четырехугольника, предложить задание:
Сформулируйте утверждение, обратное свойству вписанного четырехугольника, и выясните его истинность (можно по учебнику).
Теорема. Если сумма противолежащих углов четырехугольника равна 180°, то около него можно описать окружность
|
IV этап. Закрепление изученного материала
|
Цель деятельности
|
Задания для самостоятельной работы
|
Совершенствовать навыки решения задач
|
(Ф) 1. Решить № 708 (а), 710.
(И) 2. Выполнить самостоятельную работу.
Вариант I
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки 5 см и 13 см. Найдите площадь этого треугольника.
Вариант II
Меньший из отрезков, на которые центр описанной окружности равнобедренного треугольника делит его высоту, равен 8 см, а основание треугольника равно 12 см. Найдите площадь этого треугольника
|
IV этап. Итоги урока. Рефлексия
|
Деятельность учителя
|
Деятельность учащихся
|
(Ф/И)
- Оцените свою работу на уроке.
- Какой этап урока оказался для вас наиболее сложным?
|
(И) Домашнее задание: № 708 (б), 709; № 729 (по желанию)
|
Технологические карты уроков по учебнику Л. С. АТАНАСЯН
ГЛАВА VIII. ОКРУЖНОСТЬ
Урок 63. Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ОКРУЖНОСТЬ»
Цель деятельности учителя
|
Создать условия для систематизации теоретического материала главы; совершенствовать навыки решения задач по теме «Окружность»
|
Термины и понятия
|
Описанная окружность, вписанная окружность, описанный четырехугольник, вписанный четырехугольник
|
Планируемые результаты
|
Предметные умения
|
Универсальные учебные действия
|
Умеют применять изученные понятия, результаты и методы для решения задач
|
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий.
Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность, контролировать процесс и результат учебной математической деятельности.
Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение.
Личностные: проявляют познавательный интерес к предмету
|
Организация пространства
|
Формы работы
|
Фронтальная (Ф); индивидуальная (И); парная (П)
|
Образовательные
ресурсы
|
• Учебник.
• Задания для индивидуальной, парной работы
|
I этап. Актуализация опорных знаний учащихся
|
Цель деятельности
|
Совместная деятельность
|
Проверить выполнение домашнего задания
|
(Ф) 1. Анализ самостоятельной работы.
2. Теоретический тест (см. Ресурсный материал). Тест проводится с целью систематизации теоретического материала. После завершения выполнения работы проводится взаимопроверка. Учитель выводит на экран правильные ответы
|
II этап. Решение задач
|
Цель деятельности
|
Деятельность учителя
|
Деятельность учащихся
|
Совершенствовать навыки решения задач
|
(Ф)
1. На доске и в тетрадях решить № 719 и 732.
(П). 2. Решить в парах задачу.
Найдите периметр прямоугольника, вписанного в окружность радиуса 7,5 см, если стороны прямоугольника относятся как 3 : 4
|
№ 719

∠ADC + ∠ADE = 180°, так как они смежные => ∠ADC = 180° - ∠ADE.
∠ADE - вписанный => ∠ADE = ∪AE : 2.
∠BAD - вписанный ∠BAD = ∪BD : 2.
В треугольнике ACD сумма углов равна 180° => ∠ACD = 180° - (∠CAD + ∠АDC) = 180° -(∠BAD + 180° - ∠ADE) = ∠ADE - ∠BAD = ∪AE : 2 - ∪ВD : 2 = (∪AE - ∪BD) : 2.
№ 732.

В четырехугольнике BCMH ∠C = 90°, ∠BHM= 90°. Сумма углов выпуклого (ыВ четырехугольника равна 360° => ∠C + ∠BHM= ∠B + ∠HMC = 180°, то есть около данного четырехугольника можно описать окружность, данные углы МНС и МВС опираются на одну и ту же дугу МС, поэтому ∠MHC = ∠MBC.
Решение:

Так как прямоугольник ABCD вписан в окружность, то его диагональ является 1 диаметром данной окружности, то есть АС = 2 ∙ 7,5 = 15 см.
∆АВС - прямоугольный, АВ : ВС = 3 : 4 по условию задачи (АВ = 3х, ВС = 4х), АС = 15 см.
По теореме Пифагора АС2 = АВ2+ ВС2, то есть (3х)2+ (4х)2 = 152, откуда х = 3, АВ = 9 см , ВС = 12 см, тогда PABCD = 2 ∙ (9 + 12) = 42 см.
Ответ: 42 см
|
III этап. Итоги урока. Рефлексия
|
Деятельность учителя
|
Деятельность учащихся
|
(Ф/И)
- Оцените себя на каждом этапе урока.
- Какой этап оказался для вас наиболее сложным?
|
(И) Домашнее задание: домашняя самостоятельная работа (см. Ресурсный материал)
|
|
|
|
|
|
Ресурсный материал
Теоретический тест
Задание: заполните пропуски, чтобы получилось верное утверждение или правильная формулировка определения, теоремы, свойства.
Вариант I
1. Прямая и окружность имеют две общие точки, если расстояние от ... до ... меньше ...
2. Если прямая АВ - касательная к окружности с центром О и В - точка касания, то прямая АВ и ... ОВ ...
3. Угол АОВ является центральным, если точка О является ... а лучи ОА и ОВ ...
4. Вписанный угол, опирающийся на диаметр,...


Если хорды АВ и CD окружности пересекаются в точке Е, то верно равенство ...

Если АВ - касательная, AD - секущая, то выполняется равенство ...
8. Если четырехугольник ABCD вписан в окружность, то ...
9. Центр окружности, вписанной в треугольник, совпадает с точкой ...
10. Если точка А равноудалена от сторон данного угла, то она лежит на ...
11. Если точка В лежит на серединном перпендикуляре, проведенному к данному отрезку, то она ...
12. Около любого ... можно описать окружность.
Вариант II
1. Прямая и окружность имеют только одну общую точку, если расстояние от ... до ... равно ...
2. Если прямая CD проходит через конец радиуса ОК и CD ⊥ ОК, то CD является ... к данной окружности.
3. Угол АВС является вписанным, если точка В ... а лучи ВА и ВС ...
4. Вписанные углы равны, если они ... на одну ...


Если отрезки АВ и АС- отрезки касательных к окружности, проведенных из одной точки, то ...

Если АС и АЕ - секущие, то выполняется равенство ...
8. Если четырехугольник описан около окружности, то ...
9. Центр окружности, описанной около треугольника, совпадает с точкой ...
10. Если точка С равноудалена от концов данного отрезка, то она лежит на ...
11. Если точка D лежит на биссектрисе данного угла, то она ...
12. В любой... можно вписать окружность.
Домашняя самостоятельная работа
1. Две окружности касаются внутренне в точке В, АВ - диаметр большей окружности. Через точку А проведены две хорды, которые касаются меньшей окружности. Угол между хордами равен 60°. Найдите длины этих хорд, если:
Вариант I: радиус большей окружности равен R;
Вариант II: радиус меньшей окружности равен r.
2. Найдите углы треугольника, две стороны которого видны из центра описанной окружности под углами:
Вариант I: 100° и 140°.
Вариант II: 10° и 40°.
3. Высота и медиана, проведенные из одной вершины треугольника, делят его угол на части, градусные меры которых относятся как:
Вариант I: 5 : 8 : 5
Вариант II: 4 : 7 : 4.
Найдите углы треугольника.
Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
|
|
|
 Скачать 256.64 Kb.
Скачать 256.64 Kb.


















