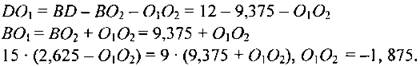Свойство вписанного четырехугольника

Название	Свойство вписанного четырехугольника
Дата	30.09.2022
Размер	256.64 Kb.
Формат файла
Имя файла	8kl_geom_tehn_karty_avt_atanasyan.docx
Тип	Урок #707189
страница	2 из 3

1 2 3

ГЛАВА VIII. ОКРУЖНОСТЬ

Урок 64. Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ОКРУЖНОСТЬ»

Цель деятельности учителя		Создать условия для систематизации теоретического материала главы, подготовки к контрольной работе; совершенствовать навыки решения задач по теме «Окружность»
Термины и понятия		Описанная окружность, вписанная окружность, описанный четырехугольник, вписанный четырехугольник, вписанные углы, центральные углы, дуги
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют применять изученные понятия и методы для решения задач			Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, работать в группе. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы		• Учебник. • Задания для групповой работы
	I этап. Решение задач
Цель деятельности	Совместная деятельность
Способствовать подготовке к контрольной работе путем решения задач разного уровня сложности	1. Собрать домашние самостоятельные работы. (Г) 2. Каждой группе даются одинаковые задачи. Учащиеся решают их, затем проводится обсуждение и презентация решений. Задача 1. Через точку А окружности проведены диаметр АС и две хорды АВ и AD так, что хорда АВ равна радиусу окружности, точка D делит полуокружность АС на две равные дуги. Найдите углы четырехугольника ABCD, если точки С и D лежат по разные стороны от диаметра АС. 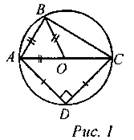Решение: 1) ∠ABC = ∠ADC = 90°, как вписанные углы, опирающиеся на диаметр. 2) ∆АОВ - равносторонний, так как АО = ВО как радиусы, а хорда АВ равна радиусу, тогда ∠BAO = 60°, ∠BCO = 30°. 3) Точка D делит полуокружность АС на две равные дуги AD и DC, поэтому хорды AD и DC равны, то есть ∆ADC - равнобедренный прямоугольный, поэтому ∠DAC =∠DCA = 45°. 4) ∠BAD = ∠BAC + ∠DAC = 60° + 45° = 105°. 5) ∠BCD = ∠BCO + ∠DCA = 30° + 45° = 75°. Задача 2. Основание равнобедренного треугольника равно 18 см, а высота, проведенная к нему, равна 12 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. 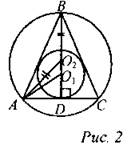Решение: ∆AO₂D - прямоугольный, по теореме Пифагора АО₂² = AD² + DO₂². Точка O₂ - центр описанной окружности - лежит на биссектрисе, медиане, высоте, а значит, на серединном перпендикуляре, проведенном к основанию. 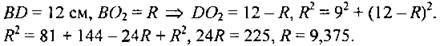Центр вписанной окружности также лежит на BD. АО₁ - биссектриса ∠BAC, следовательно АВ : ВО₁ = AD : DO₁. По теореме Пифагора в ∆ABD: АВ² = AD² + BD² = 81 + 144 = 225, значит, АВ = 15 см. 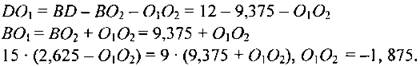Так как ВO₂ = R, то: Так как O₁O₂ < 0 => О₁ лежит между точками В и O₂, тогда DO₁ - O₁O₂= 2,625 + 1,875 = 4,5 см
II этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И). - Проанализируйте свою работу в группе, выражая это словами: «помощь», «вместе», «совет», «один», «помогли», «все», «посоветовал», «рассказывал», «подружились», «друг» и т. п.				(И) Домашнее задание: решить № 732, 725, 726; подготовиться к контрольной работе

ехнологические карты уроков по учебнику Л. С. Атанасяна - 2015

ГЛАВА VIII. ОКРУЖНОСТЬ

Урок 65. Тема: КОНТРОЛЬНАЯ РАБОТА № 5

Цель деятельности учителя	Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала
Термины и понятия	Окружность, дуга окружности, радиус, вписанная окружность, описанная окружность
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности			Познавательные: умеют проводить сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Учебник. • Задания для индивидуальной работы
I этап. Выполнение контрольной работы
Цель деятельности	Задания для контрольной работы
Проверить знания, умения и навыки решения задач	Вариант I 1. Через точку А окружности проведены диаметр АС и две хорды АВ и AD, равные радиусу этой окружности. Найдите углы четырехугольника ABCD и градусные меры дуг АВ, ВС, CD, AD. 2. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. Вариант II 1. Отрезок BD - диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна ему. Найдите углы четырехугольника ABCD и градусные меры лут АВ, ВС, CD, AD. 2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. Вариант III (для более подготовленных учащихся) 1. МА и МВ - секущие, АС и BD - хорды окружности с центром О. Докажите, что ∠AOB = ∠AKB + ∠AMB. 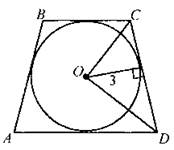2. Площадь равнобедренной трапеции ABCD с основаниями ВС и AD, описанной около окружности с центром О и радиусом 3 см, равна 60 см². Найдите радиус окружности, описанной около треугольника OCD.
II этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
		(И). Домашнее задание: повторить главу V «Четырехугольники»

Технологические карты уроков по учебнику Л. С. Атанасяна - 2015

ГЛАВА VIII. ОКРУЖНОСТЬ

Урок 66. Тема: ПОВТОРЕНИЕ ПО ТЕМАМ «ЧЕТЫРЕХУГОЛЬНИКИ», «ПЛОЩАДЬ»

Цель деятельности учителя	Создать условия для организации повторения основных теоретических фактов по заданной теме
Термины и понятия	Выпуклые многоугольники, сумма углов выпуклого многоугольника, формулы площадей, параллелограмм, прямоугольник, трапеция, квадрат, ромб
Планируемые результаты
Предметные умения				Универсальные учебные действия
Умеют применять изученные понятия, результаты и методы для решения задач				Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, контролировать себя. Личностные: проявляют ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Учебник. • Задания для индивидуальной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности		Совместная деятельность
Систематизировать ошибки, допущенные в контрольной работе		(Ф/И) 1. Разбор задач, с которыми не справились большинство учеников. 2. Работа над ошибками с использованием ответов и указаний к задачам контрольной работы по необходимости. Индивидуальная помощь учителя менее подготовленным учащимся
II этап. Тест на повторение
Цель деятельности		Задания для самостоятельной работы
Проверить уровень сформированности теоретических знаний		(Ф/И) Задания теста выполняются самостоятельно с последующей самопроверкой и обсуждением заданий, в которых допущены ошибки (см. Ресурсный материал)
III этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) - Оцените свою работу на уроке. - Какие трудности возникли у вас и почему?			(И) Домашнее задание: повторить признаки подобия треугольников; решить задачи: 1) На стороне ВС прямоугольника взята точка М так, что AM = 13 см, АВ = 12 см, В = 20 см. Найдите: а) МС; б) площадь четырехугольника AMCD. 2) В треугольнике АВС АВ = АС. Высота ВМ равна 9 см и делит боковую сторону на два отрезка так, что АМ = 12 см. Найдите площадь и периметр треугольника

Ресурсный материал

Тест

Верно ли, что:

1. Сумма углов выпуклого четырехугольника равна 360°.

2. В трапеции углы при каждом основании равны.

3. Квадрат - это параллелограмм, у которого все углы прямые.

4. Вершины А и С ромба ABCD симметричны относительно прямой BD.

5. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные им отрезки.

6. Отрезок, соединяющий точки, лежащие на боковых сторонах трапеции, параллелен основаниям и равен их полусумме.

7. Параллелограмм, у которого все углы равны и все стороны равны, является квадратом.

8. Биссектриса одного из углов параллелограмма отсекает от него равнобедренный треугольник.

9. Площадь прямоугольной трапеции равна произведению ее средней линии на боковое ребро.

10. Площадь ромба равна половине произведения его диагоналей на синус угла между ними.

11. Если в треугольниках АВС и А₁В₁С₁ высоты АН и А₁Н₁ равны, то

12. Площадь прямоугольного треугольника равна произведению его катетов.

13. Если в ААВС стороны равны 5, 6, 7 см, то его площадь равна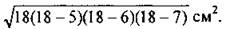

14. Если в треугольниках АВС и А₁В₁С₁∠A = ∠A₁, то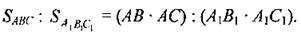

15. Медианы треугольника делят треугольник на шесть равновеликих треугольников.

Укажите верный ответ из предложенных:

1. Сумма углов выпуклого пятиугольника равна:

а) 360°;

б) 900°;

в) 540°.

2. Один из углов равнобедренной трапеции равен 100°. Три оставшихся угла равны:

а) 80°, 80°, 100°;

б) 75°, 75°, 110°;

в) 70°, 70°, 120°.

3. Смежные стороны прямоугольника равны 6 и 8 см. Диагонали его равны:

а) √28 и √28 см;

б) 10 и 10 см;

в) 14 и 14 см.

4. Сторона ромба равна 5 см, а одна из его диагоналей 6 см. Площадь ромба равна:

а) 30 см²;

б) 24 см²;

в) 15 см².

5. В ромбе ABCD ∠A = 70°, ∠ABC равен:

а) 20°;

б) 110°;

в) 55°.

6. В параллелограмме разность смежных сторон равна 5 см, а его периметр равен 38 см. Меньшая сторона параллелограмма равна:

а) 7 см;

б) 12 см;

в) 9,5 см.

7. Биссектриса угла А прямоугольника ABCD пересекает ВС в точке Е так, что BE = 4,5 см, СЕ = 5,5 см. Площадь прямоугольника равна:

а) 55 см²;

б) 100 см²;

в) 45 см².

8. Одна из диагоналей ромба равна его стороне. Углы ромба равны:

а) 90°, 90°, 90°, 90°;

б) 60°, 60°, 120°, 120°;

в) 45°, 45°, 90°, 90°.

9. Ромб, не являющийся квадратом, имеет n осей симметрии. Значение n равно:

а) 1;

б) 2;

в) 4.

10. Площадь ромба со стороной 8 см и углом 60° равна:

а) 32 см²;

б) 32√3 см²;

в) 16√3 см².

11. Площадь прямоугольника с гипотенузой 26 см, один из катетов которого равен 24 см, равна:

а) 120 см²;

б) 312 см²;

в) 240 см².

12. Площадь равнобедренного треугольника с боковой стороной 13 см и основанием 24 см равна:

а) 120 см²;

б) 156 см²;

в) 60 см².

13. Одна из сторон параллелограмма равна 14 см, а высота, проведенная к ней, — 12 см. Высота, проведенная к смежной стороне, равной 21 см, равна:

а) 8 см;

б) 10 см;

в) 19 см.

14. Площадь равнобедренной трапеции с основаниями 10 см и 16 см и боковой стороной 5 см равна:

а) 104 см²;

б) 52 см²;

в) 65 см².

15. Площадь квадрата со стороной 5√2 см равна:

а) 50 см²;

б) 25 см²;

в) 100 см².

Ответы к первой части теста:

Верно: 1,4, 5, 7, 8, 10, 11, 14, 15.

Неверно: 2, 3, 6, 9, 12, 13.

Ответы ко второй части теста:

11	22	33	44	55	66	77	88	99	10	11	12	13	14	15
Вв	Аа	Бб	Бб	Вв	Аа	Вв	Бб	Бб	б	а	в	а	б	а

Технологические карты уроков по учебнику Л. С. Атанасяна - 2015

1 2 3