Учебный курс для студентов очной и заочной форм обучения
 Скачать 5.65 Mb.
|
|
Основы теории расчета ременных передач. Силы и напряжения в ремнях, кривые скольжения и допускаемые полезные напряжения Силы натяжения в ветвях ремня (Fo, Fx, F2). Для создания необходимого трения между ремнем и ободом шкива ре мень должен иметь достаточную силу начального натяжения Fo. Это дости гается предварительным натяжением ремня при монтаже или с помощью подвижной опоры. Чем больше Fo, тем выше тяговая способность переда чи. Но при большом начальном натяжении ремень получает и большую вытяжку, снижается его долговечность. Поэтому Foвыбирают таким, чтобы ремень мог сохранить это натяжение достаточно длительное время, не по лучая большой вытяжки. Начальную силу натяжения ремня определяют по формуле Fo= Аσ0, (16) где А — площадь поперечного сечения ремня; с0 — начальное напряжение в ремне. Приближенно можно считать, что в состоянии покоя и при холостом ходе каждая ветвь натянута одним и тем же усилием Fo(рис. 12, а) 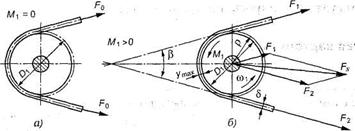 Рис.12. Усилия в ветвях ремня: а — на холостом ходу; б — при передаче нагрузки С приложением момента T1 ведущая ветвь натягивается до значения F1, натяжение ведомой ветви уменьшается до F2(рис.12, б). Силы натяжения F1 и F2, можно определить из условия равновесия шкива  (17)Отсюда  (18)С учетом того, что окружная сила на шкиве  (19)получим  (20)Так как сумма сил натяжения ветвей ремня постоянна (независимо от того, нагружена передача или нет), то  (21)Из равенств (20) и (21) следует, что  (22)Эти уравнения устанавливают изменение натяжений ведущей и ведомой ветвей в зависимости от нагрузки Ft, но не вскрывают способности передавать эту нагрузку или тяговой способности передачи, которая связана со значением силы трения между ремнем и шкивом. Такая связь установлена Эйлером в виде . (23) Решая совместно уравнения (17) и (23) с учетом (21), находим: 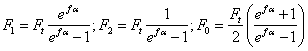 . (24)Формулы (24) устанавливают связь сил натяжения ветвей работающей передачи с нагрузкой Ftи факторами трения f и . Они позволяют также определить минимально необходимое предварительное натяжение ремня Fo,при котором еще возможна передача заданной нагрузки Ft. Если , то начнется буксование ремня. Можно установить по формуле (24), что увеличение значений f и благоприятно сказывается на работе передачи. Эти выводы принимаются за основу при создании конструкций клиноременной передачи и передачи с натяжным роликом. В первой передаче использован принцип искусственного повышения трения путем заклинивания ремня в канавках шкива. Во второй – увеличивают угол обхвата установкой натяжного ролика. При обегании ремнем шкивов возникают центробежные силы Fv, которые отбрасывают ремень от шкива:  (25)где — плотность материала ремня, кг/м3; А = bδ — площадь сечения ремня, м2; и — окружная скорость, м/с. С учетом центробежной силы натяжения определяют по следующим формулам для холостого хода:  (26)для ведущей ветви  (27)для ведомой ветви  (28)Натяжение Fvослабляет полезное действие предварительного натяжения Fo. Оно уменьшает силу трения и тем самым понижает нагрузочную способность передачи. Как показывает практика, влияние центробежных сил на работоспособность передачи существенно только при больших скоростях: v > 20 м/с. Нагрузка на валы и опоры Fs. Силы натяжения ветвей ремня Р{и F2, (за исключением силы Fv) пере даются на валы и опоры. Рассматривая параллелограмм сил (см. рис.12, б), находят равнодействующую сил  (29)где — угол между ветвями ремня. Поставим в выражение (29) вместо (F1 + F2) величину 2F0[см. форму лу (21)]; получим  (30)Выражение (30) можно преобразовать через окружную силу Fr. В этом случае можно считать, что для прорезиненных и кожаных ремней Fs>>2,5Ft); для хлопчатобумажных Fs>>3Ft); для шерстяных Fs >> 4Ft). Таким образом, на грузка на валы в 2,5—4 раза превышает окружную силу Ft, что является не достатком ременных передач. Напряжения в ремне. При работе ременной передачи напряжения в различных сечениях по длине ремня неодинаковы. Изобразим эти напря жения отрезками соответствующей длины, проведя их перпендикулярно поверхности ремня. Получим эпюру суммарных напряжений (рис.13). 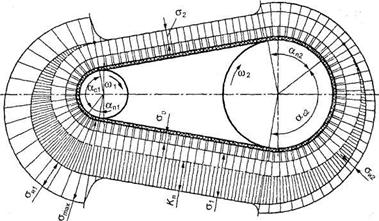 Рис.13. Напряжения в поперечных сечениях ремня Различают следующие виды напряжений в ремне. 1. Предварительное напряжение , определяемое в зависимости от силы начального натяжения: σ0=F0/A, (31) где А — площадь поперечного сечения ремня. Для стандартных ремней рекомендуется принимать: = 1,76 МПа — для плоских ремней; = 1,18 - 1,47 МПа — для клиновых. 2. Удельная окружная сила (полезное напряжение) Кп. Это напряжение зависит от передаваемой ремнем окружной силы F;. Kn=Ft/A. (32) Полезное напряжений можно определить и как разность напряжений и : (33) где и — напряжения в ведущей и ведомой ветвях. По значению КПоценивается тяговая способность ременной передачи. 3. Напряжение изгиба , возникающее в сечениях ремня при огибании шкивов (см. рис.13) и изменяющееся по пульсирующему циклу. В плос ком ремне нейтральный слой проходит посередине толщины ремня. На ружные слои ремня при огибании шкива растягиваются, а внутренние — сжимаются. Приближенно примем, что закон Гука справедлив и для мате риалов ремней, тогда для растянутой стороны ремня , где s = утт/р — относительное удлинение волокон. С учетом того, что утax = 0,5 , а р = 0,5(D1 + 8) (см. рис.12, б), пренеб регая величиной 8 по сравнению с D1),, получим: (34) где Е — модуль продольной упругости материала ремня; — толщина рем ня; D1 — диаметр огибаемого шкива. В расчетах для плоскоременных передач ограничивается минималь но допустимым значением (см. табл.1). На тяговую способность передачи напряжение изгиба не влияет, но яв ляется основной причиной усталостного разрушения ремня. 4. Напряжение от центробежных сил. Это напряжение зависит от силы Fv (35) На рис.13 показано, что по всей длине ремня напряжение распре деляется равномерно. 5. Наибольшее суммарное напряжение определяется как сумма по лезного напряжения, напряжения изгиба в ведущей ветви ( и ) и на пряжения от центробежных сил ( ): (36) ( возникает в ремне, в месте его набегания на малый шкив (см. рис.13)). Рассмотренные напряжения в ветвях ремня используются в дальней шем при расчете ременных передач на тяговую способность, для определе ния максимального напряжения в ремне и т. п. Следует отметить, что прочность ремня не является достаточным усло вием, определяющим работоспособность ременной передачи. Желательно, чтобы передача обеспечивала как можно большее значение силы F1, при неизменном для данного ремня значении начальной силы натяжения 2F0. Скольжение ремня. Как показали экспериментальные исследова ния, упругое скольжение ремня по шкиву возникает в нормально работаю щей передаче. Причиной упругого скольжения является неодинаковость натяжения веду щей и ведомой ветвей. При обегании ремнем ведущего шкива его натяжение падает, от F1до F2(причем всегда F1 > F2); ремень, проходя шкив, укорачива ется, вследствие чего возникает упругое скольжение. На ведомом шкиве происходит аналогичное явление, но здесь ремень удлиняется, так как на тяжение от F2возрастает до F1. Упругое скольжение происходит не по всей длине дуги обхвата ремнем шкива. Установлено, что угол дуги обхвата разделяется на две части — дугу упругого скольжения ( ) и дугу покоя ( ), на которой упругое сколь жение отсутствует (см. рис. 13). При перегрузке передачи скольжение происходит по дуге , т.е. ремень скользит по всей поверхности касания со шкивом. Такой вид скольжения называют буксованием. При упругом скольжении скорости по длине ремня неодинаковы. Скорость ремня и окружная скорость шкива совпадают лишь на дуге по коя со стороны набегающей ветви. Это позволяет оценить упругое про скальзывание. Коэффициент упругого скольжения:  (37)где и - окружные скорости ведущего и ведомого шкивов. При нормальном режиме работы ременной передачи значение = 0,01 ÷ 0,02. Коэффициент тяги и кривые скольжения. В результате исследова ния кривых скольжения (рис.14), построенных по опытным данным, ус тановлена связь между полезной нагрузкой (окружной силой F) и предва рительным натяжением ремня Foв зависимости от коэффициента скольже ния . 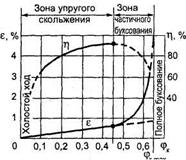 Рис.14. Кривые скольжения и КПД ременной передачи Отношение передаваемой ремнем ок ружной силы к сумме натяжений его ветвей называют коэффициентом тяги:  (38)Коэффициент тяги характеризует нагру зочную способность передачи. На этом гра фике (см. рис.14) по оси абсцисс отложе ны значения коэффициента тяги , а по оси ординат — коэффициент скольжения и КПД передачи . На начальном участке кривой скольже ния (от 0 до ) наблюдается только упру гое скольжение. Линия этого участка приближается к прямой. Здесь зна чения КПД и падают с уменьшением нагрузки. Дальнейшее увеличение нагрузки (т.е. увеличение ) приводит к буксованию. В зоне частичного буксования наблюдаются как упругое скольжение, так и буксование. При рабочую нагрузку следует принимать в пределах, которые соответствуют наибольшему значению КПД. Работа в зоне частичного бук сования допускается только в момент пуска передачи (т.е. для кратковре менных перегрузок).Работу в зоне частичного буксования допускают только при кратковременных перегрузках, например, в момент запуска двигателя. В этой зоне КПД резко снижается вследствие увеличения потерь на скольжение ремня, а ремень быстро изнашивается. Размер зоны частичного буксования характеризует способность передачи воспринимать кратковременные перегрузки.
Потери мощности в ременной передаче складываются из потерь в опорах валов; потерь на внутреннее трение в ремне, связанное с периодическим изменением деформаций, и в основном с деформациями изгиба; потерь от сопротивления воздуха движению ремня и шкивов. Все эти потери трудно оценить расчетом, а поэтому КПД передачи определяют экспериментально. При нагрузках, близких к расчетным, среднее значение КПД для плоскоременных передач = 0,97, для клиноременных = 0,96. Допускаемые напряжения в ремне. 1. Допускаемое приведенное полезное напряжение Ко. Из графика на рис.14 видно, что оптимальное значение коэффици ента тяги определяет максимальную полезную окружную силу Flmax. При этом условии ременная передача с начальным натяжением Foможет работать без пробуксовки. Из выражения (38)  (39)где — оптимальный коэффициент тяги. Если обе части равенства (39) разделить на площадь поперечного сечения ремня А, то получим  (40)здесь  — допускаемое приведенное полезное напряжение в рем не, соответствующее коэффициенту тяги . Значение Ко сучетом табл.1 можно определить для плоскоременной передачи по формуле где s и — постоянные коэффициенты, зависящие от материала ремня и . Для клиноременной передачи Коопределяется по табл.6. Таблица 6. Значения K0для клиновых ремней
| ||||||||||||||||||||||||||||||