методика. ММП ПР 4. Учебник по математике 4 класс Моро. М. И. Ууд пример задания из учебника
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
VI. ФизкультминуткаУчитель включает аудиокассету. Под музыку песни "Чему учат в школе" дети выполняют физические упражнения.  VII. Закрепление пройденного материала (продолжение)У. Мы прилетели на планету Марс. На карте-схеме проводится линия. – Вы хотели бы что-нибудь узнать об этой планете? Марс – планета Солнечной системы, четвертая от Солнца. По усмотрению учителя можно подобрать материал для небольшого сообщения о Марсе. Вот какое задание вам предлагается на Марсе: Найдите знакомые вам геометрические фигуры. Вспомните, как они называются. На магнитной доске открывается второй лист методического пособия "книжка". 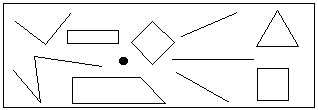 Дети отвечают. – А теперь давайте сделаем некоторые построения. На классной доске построение выполняет учитель, дети работают в тетрадях, выполняя все этапы задания. – Начертите прямую линию. Можем ли мы изобразить всю прямую? Д. Нет. У. Почему? Д. Она продлевается в обе стороны бесконечно. У. Что же мы чертим? Д. Часть прямой. У. Отметьте на ней точку А. Как получить отрезок? Д. Надо поставить еще точку. У. Обозначим ее буквой С. Назовите отрезок. 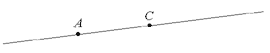 Д. Отрезок АС. У. Что такое отрезок? Д. Часть прямой, ограниченная двумя точками. У. Отметьте красным карандашом отрезок АС. Как называются незакрашенные части прямой? Д. Лучи. У. Верно. Покажите их. Что такое луч? Д. Часть прямой, у которой есть начало, но нет конца. Учитель раздает детям веревочки. У. А сейчас попробуем получить эти фигуры практически – на веревочке. Ваши пальчики – это точки. Покажите отрезок. Покажите луч. Дети выполняют задание. – Молодцы! Летим дальше. Наш путь лежит на планету Юпитер. Пока ракета идет на автопилоте, вам предстоит выполнить еще одно интересное задание. На столе у вас перфокарты. Надо самостоятельно найти периметр фигуры, данной в ней. Детям предложено четыре варианта карточек. Они выполняют задание, записывая решение в тетрадях. – Мы прибыли на планету Юпитер (на карте-схеме проводится линия). Это самая большая планета Солнечной системы. Посмотрите на карту-схему. Какая геометрическая фигура изображает наш маршрут? Д. Ломаная. У. Сколько в ней звеньев? Д. Три. У. Постройте самостоятельно ломаную из трех звеньев с длинами 7 см, 3 см, 2 см. Работаем цветными карандашами. Найдите длину ломаной, начертите отрезок такой же длины. Дети выполняют задание. – Много интересных математических заданий выполнили мы, путешествуя по планетам Солнечной системы. Пора возвращаться на Землю, где нас любят и ждут. Чтобы вернуться, надо дружно всем вместе отгадать кроссворд. VIII. Итог урокаНа магнитной доске – третий лист методического пособия "книжка".  1. Мера длины, состоящая из 10 дм. 2. Геометрическая фигура с равными сторонами, но непрямыми углами. 3. Часть прямой, у которой есть начало, но нет конца. 4. Самая маленькая геометрическая фигура. 5. Прямоугольник с равными сторонами. 6. Знак (символ) для обозначения числа. 7. Следующее число за числом 3. Ответы: 1. Метр. 2. Ромб. 3. Луч. 4. Точка. 5. Квадрат. 6. Цифра. 7. Четыре. У. Какое слово получилось в выделенных клетках? Д. Молодцы. На карте-схеме проводится линия к Земле. Звучит музыка "Приземление". У. Из полета возвратились И на Землю приземлились. О чем вы расскажете дома? Начните свой ответ с любого из таких предложений. На магнитной доске – четвертый лист методического пособия "книжка".
Выслушиваются ответы детей. Задание 4. Разработайте фрагмент урока по исследованию свойств прямоугольника. Фрагмент урока должен содержать следующие этапы: 1. Актуализация знаний. 2. Организация учебного исследования. 3. Применение полученных знаний. Ответ: Устный счет. 1) Математическая разминка – 17 увеличить на 8. (Слайд 2) – 22 уменьшить на 6. (Слайд 3.) – Первое слагаемое 19, второе – 6. Вычислить сумму. (Слайд 4) – Найдите сумму 7 и 5. (Слайд 5) – Уменьшаемое 15, вычитаемое 9. Чему равна разность? (Слайд 6) – Найдите разность 24 и 16, 12 и 7. (Слайд 7) – На сколько 18 больше 9? (Слайд 8) – На сколько 8 меньше 16? (Слайд 9) Взаимопроверка (дети обмениваются тетрадями). (Слайд 10) 2) Игра: "Найдите лишнее выражение". (Слайд 11) 37-7 70-40 62-32 20+10 100-70 76-36 – Докажите. 3) Задачи. Мальчик за 1 четверть исписал 6 тетрадей, а за вторую – 4 тетради. Сколько всего тетрадей он исписал за 2 четверть? У Игоря и Жени 11 голубей. У Жени 7 голубей. Сколько голубей у Игоря? 4) На смекалку. На ветке сидели 5 синиц и 7 воробьев. 6 птиц улетели. Улетел ли хоть один воробей? Игра: "Геометрия вокруг нас". (Слайд 12) – По координатам букв прочитайте слово и скажите, что оно означает. (1;3), (2;4), (3;3), (1;1), (2;4), (2;2), (3;1), (4;2), (4;4). Г Е О М Е Т Р И Я – Что означает слово "Геометрия"? Геометрия – раздел математики, изучающий пространственные отношения и формы (из "Толкового словаря" С. И. Ожегова). 2) Назовите геометрические фигуры: (Слайд 13) – Назовите предметы или части предметов, которые имеют такую геометрическую форму. – Для чего нам нужно знать свойства геометрических фигур? Вывод (делают дети): Чтобы сделать мебель или другие предметы мы должны знать свойства геометрических фигур. – Какие две геометрические фигуры можно назвать одним словом?– Докажите, что эти фигуры прямоугольники 3) Работа в парах. Найдите среди геометрических фигур прямоугольники. (Слайд 14) (Чертеж на слайде и у детей). – Как проверили? (фигуры 3 и 4 – прямоугольники) (У этих фигур все углы прямые). (Использовали угольник, модель прямого угла). – Положите перед собой только прямоугольник, уберите квадрат. Возьмите линейку. Измерьте длины противоположных сторон прямоугольника. Сделайте вывод (слайд 9). – Соедините противоположные углы прямоугольника прямой линией. Вы получите две линии. Может быть, кто-то из вас знает, как они называются? Эти линии называются диагоналями. Измерьте длины диагоналей прямоугольника. Сделайте вывод. – Что нового вы узнали о прямоугольнике? – Скажите, где мы можем проверить свои выводы? – Откройте учебник на стр.116. прочитайте правило. – Теперь вы можете сформулировать тему нашего урока. – Назовите свойства прямоугольника ( слайд 10) – Какова цель сегодняшнего урока? – Как вы думаете, важно только знать свойства прямоугольника? Что нам необходимо в достижении цели? Давайте, составим план урока. 1.Узнать свойства прямоугольника. 2.Применять знания. 3.Повторить пройденное. Что нам поможет в достижении цели? Длины противоположных сторон прямоугольника равны. Ответы детей Мы узнали, что противоположные стороны прямоугольника имеют одинаковую длину. Диагонали тоже. Надо воспользоваться учебником. Свойства прямоугольника. Познакомиться со свойствами прямоугольника. Составить план Учебник, учитель. Задание 4. Изучив методическую литературу, составьте классификацию простых задач, с решением которых знакомятся учащиеся начальной школы. Ответ: В методическом отношении удобна следующая классификация простых задач: деление задач на группы в зависимости от тех понятий, которые формируются при их решении. С этой точки зрения выделяют три группы задач. 1-я группа - простые задачи на усвоение конкретного смысла арифметических действий. В эту группу входят такие задачи: 1) Нахождение суммы двух чисел. Маляр покрасил в одной квартире 6 дверей, а в другой 4. Сколько дверей покрасил маляр? 2) Нахождение остатка. Школьники сделали 6 кормушек. 2 кормушки они повесили в школьном саду. Сколько кормушек им осталось повесить? 3) Нахождение суммы одинаковых слагаемых (произведения). Школьники посадили в парке 4 ряда березок по 5 штук в ряду. Сколько березок они посадили? 4) Деление на равные части. В 3 палатках жили 24 туриста, в каждой палатке поровну. Сколько туристов жили в каждой палатке? 5) Деление по содержанию. Каждая бригада школьников окопала по 8 яблонь, а всего школьники окопали 24 яблони. Сколько всего бригад школьников выполняли эту работу? 2-я группа - простые задачи на усвоение связи между компонентами и результатами арифметических действий. В эту группу входят такие задачи: 1) Нахождение первого слагаемого по известным сумме и второму слагаемому. У кормушки было несколько снегирей, к ним прилетели 6 синиц. И их стало всего 9. Сколько снегирей было у кормушки? 2) Нахождение второго слагаемого по известным сумме и первому слагаемому. У кормушки было 3 снегиря, к ним прилетели несколько синиц и их стало 9. Сколько синиц прилетело? 3) Нахождение уменьшаемого по известным вычитаемому и разности. Школьники сделали несколько скворечников. Когда 2 скворечника они повесили на дерево, то у них осталось 4 скворечника. Сколько скворечников сделали школьники? 4) Нахождение вычитаемого по известному уменьшаемому и разности. Школьники сделали 6 скворечников. Когда несколько скворечников они повесили на дерево, то у них осталось еще 4 скворечника. Сколько скворечников повесили школьники? 5) Нахождение первого множителя по известным произведению и второму множителю. Неизвестное число умножили на 8 и получили 32. Найти неизвестное число. 6) Нахождение второго множителя по известным произведению и первому множителю. 9 умножили на неизвестное число и получили 27. Найти неизвестное число. 7) Нахождение делимого по известным делителю и частному. Неизвестное число разделили на 9 и получили 4. Найти неизвестное число. 8) Нахождение делителя по известным делимому и частному. 24 разделили на неизвестное и получили 6. Найти неизвестное число. 3-я группа - простые задачи, раскрывающие новый смысл арифметических действий: понятия разности и кратного отношения. В эту группу входят такие задачи, связанные с понятием разности: 1) Разностное сравнение чисел или нахождение разности двух чисел (1 вид). У Миши было 8 шариков, а у Коли 5 шариков. На сколько у Миши шариков больше, чем у Коли? 2) Разностное сравнение чисел или нахождение разности двух чисел (2 вид). У Тани 10 книг, а у Оли 8 книг. На сколько книг у Оли меньше? 3) Увеличение числа на несколько единиц (прямая форма). На первой тарелке было 7 груш, а на второй на 3 груши больше. Сколько груш на второй тарелке? 4) Увеличение числа на несколько единиц (косвенная форма). У Миши 4 фломастера, это на 8 фломастеров меньше, чем у Тани. Сколько фломастеров у Тани? 5) Уменьшение числа на несколько единиц (прямая форма). Школьники собрали с первой грядки 23 кг моркови, со второй на 3 кг меньше. Сколько килограммов моркови собрали со второй грядки? 6) Уменьшение числа на несколько единиц (косвенная форма). В колхозе было 12 тракторов, это на 4 больше, чем комбайнов. Сколько комбайнов было в колхозе? В эту группу также входят простые задачи, связанные с понятием кратного отношения. 1) Кратное сравнение чисел или нахождение отношения двух чисел (1вид). На проводе 6 ласточек и 2 воробья. Во сколько раз ласточек больше, чем воробьев? 2) Кратное сравнение чисел или нахождение отношения двух чисел (2 вид). В столовой израсходовали 8 кг муки и 24 кг крупы. Во сколько раз меньше израсходовали муки, чем крупы? 3) Увеличение числа в несколько раз (прямая форма). В одном куске 6 м проволоки, а в другом в 2 раза больше. Сколько метров проволоки во втором куске? 4) Увеличение числа в несколько раз (косвенная форма). У брата было 6 простых открыток, их было в 2 раза меньше, чем цветных открыток. Сколько цветных открыток было у брата? 5) Уменьшение числа в несколько раз (прямая форма). В пруду плавали 9 гусей, а уток в 3 раза меньше. Сколько уток плавало в пруду? 6) Уменьшение числа в несколько раз (косвенная форма). Длина первой доски 18 дм, это в 3 раза больше длины второй доски. Какова длина второй доски? Простые задачи на сложение и вычитание изучаются в 1 классе в связи с изучением соответствующих действий, а задачи на умножение и деление - во 2 классе. Задание 5. Выберите из учебника математики 1 класса задания (не менее 6 заданий), подготавливающие младших школьников к введению понятия «арифметическая задача». Разработайте два задания. Ответ: 1) На одной полке 5 книг, на другой – 3. Сколько книг на двух полках? Действие сложения соответствует операции объединения множеств. Поэтому внешним признаком задачи, раскрывающей смысл действия сложения, является наличие в вопросе слов «вместе», «всего» или возможности перефразирования вопроса так, чтобы в нем появилось одно из этих слов. В задаче возможна формулировка вопроса: «Сколько всего книг?» 2) У Маши 9 маков, а у Риты на 2 мака больше, чем у Маши. Сколько маков у Риты? (Прямая форма.) У Маши 9 маков, это на 2 мака меньше, чем у Риты. Сколько маков у Риты? (Косвенная форма.) Задание 6. Прочитайте задачу: «В школьную столовую привезли 6 кг лимонов, яблок на 24 кг больше, чем лимонов, а груш на 12 кг меньше, чем яблок. Сколько килограммов груш привезли в школьную столовую?» Вопросы: ¾ Каким способом (синтетическим, аналитическим или аналитико-синтетическим) лучше проводить разбор этой задачи? ¾ Покажите методику работы над арифметической задачей на примере данной задачи (этапы работы над задачей смотрите в лекции). Ответ: лимоны-6кг яблоки-?, на 24кг > груши-?, на 12кг < у вопроса про груши мы обводим главный вопрос в кружок. от яблок к лимонам проводим квадратную стрелку. от груш к яблокам проводим квадратную стрелку. 1)24+6=30 (кг)-яблоки. 2)30-12=18 (кг) Ответ:18кг груш привезли в школьную столовую. Задание 7. Разработайте контрольно-измерительные материалы для диагностики результатов обучения младших школьников по теме «Дроби». Вид контрольно-измерительных материалов по выбору. В работе должно быть не менее 10 заданий. Ответ: Математика. (ОС «Школа 2100») Тема: «Дроби» 4 класс. Цель: проверка знания ключевых понятий по данной теме («числитель», «знаменатель», «целое»); умение находить часть от числа и число по его части, сравнивать дроби с одинаковыми числителями и разными знаменателями, складывать и вычитать дроби с одинаковыми знаменателями, решать задачи по теме. Укажи дробь: А) 6 Б) 006 В) 2. В дроби над чертой пишется: А) числитель Б) делитель В) знаменатель Г) множитель 3. В дроби под чертой пишется: А) множитель Б) знаменатель В) числитель Г) делитель 4. Укажи наименьшую дробь: А) 5. Укажи наибольшую дробь: А) |
