Учебники и учебные пособия по экономике ориентированы на студентов i высшего образования для которых читаются две отдельные дисциплины вначале Экономика математические методы и прикладные модели
 Скачать 1.1 Mb.
|
|
Глава IV. Временные ряды 4.1. . Последовательность наблюдений моделируемого показателя, упорядоченная в порядке возрастания времени называется временным рядом (ВР): Уt, t=t1,t2,…,ti,…,tn; ti>ti-1. Обычно в экономических задачах временной интервал отсчетов постоянен (t=const). Тогда можно указывать просто номер отсчета. Уt, i=1,2,...,N. Замечание: 1). Уровни временных рядов Уt не являются взаимно независимыми, как того требует первая предпосылка метода наименьших квадратов. Поэтому разработаны специальные методы оценки параметров уравнения регрессии. В этом отличие временных рядов от базы данных пространственного типа. 4.2. Компонентный анализ временных рядов Уt=Ut+ Vt+ Ct+ Et, t=1,2, (4.1) 4.3. Понятие случайного процесса Стационарные временные ряды 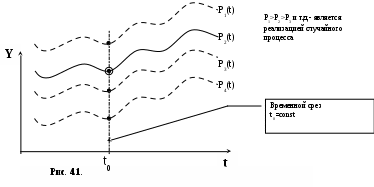 Случайный процесс (или случайная функция) неслучайного аргумента t – называется функция, которая при любом t является случайной величиной. Определение 1:Yt называется строго стационарным (стационарным в узком смысле), если в различных временных срезах t=var выполнено два условия: 1. Вид закона распределения свободных величин Y один и тот же (например – нормальный закон распределения остатков); 2. Числовые параметры закона распределения (числовые характеристики) одинаковы: M(Y(t))=a=const; D[Y(t]=2= const. Определение 2: Если выполнено только условие № 2 то временные ряды называются стационарными в широком смысле или эргодическим. Другими словами эргодический случайный процесс протекает однородно по времени. Замечание: В дисциплине «Теория вероятности и математическая статистика» показано что «Выборочные оценки вероятностных характеристик эргодического процесса могут быть вычислены по одной фиксированной реализации для наблюдений в разные моменты Уt, р=const. 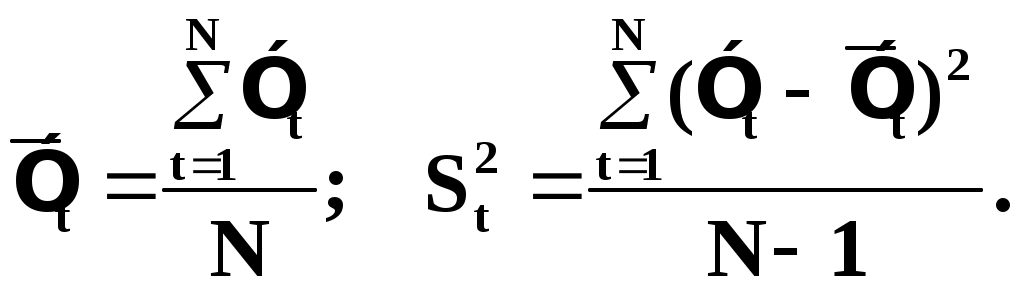 (4.2)Пример: Стационарного случайного процесса – «белый шум», т.е. возмущения Ei при условии: M[Ei]=0 M[Ei Ek]=0 – отсутствие корреляции. Если EN(0;E2), то шум нормальный (гауссовский) белый. 4.4. Понятие о коэффициенте корреляции во временном ряде (АКФ) Степень тесноты связи между последовательными уровнями временного ряда У1, У 2…, Уn и сдвинутыми на уровнями У 1+, У 2+…, Уn+ (-лаг) измеряется с помощью коэффициента автокорреляции. Его генеральное (теоретическое) значение определяется по формуле:  (4.3)Здесь благодаря свойству эргодичности временного ряда, которое постулируется: 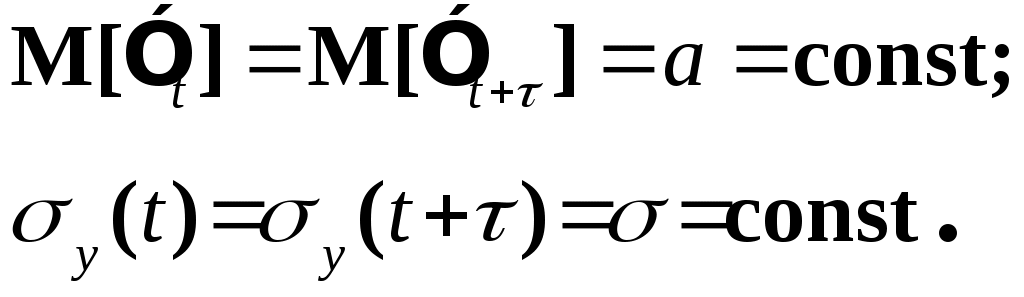 (4.4)Термин автокорреляции означает что () измеряет корреляцию между членами одного и того же временного ряда. При измерении лагового сдвига (=1,2,3,…) получим функцию (t) называемую автокорреляционной функцией (АФК.) Автокорреляционная функция () не зависит от t, а зависит только от , причем: 4.5. Выборочная оценка коэффициента автокорреляции для числа степеней свободы Вместо N имеем (N-), так как для первых моментов времени вплоть до t= () не определено: 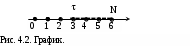 Пусть =2. Тогда () можно вычислить только начиная с t=3,4,…… 6. 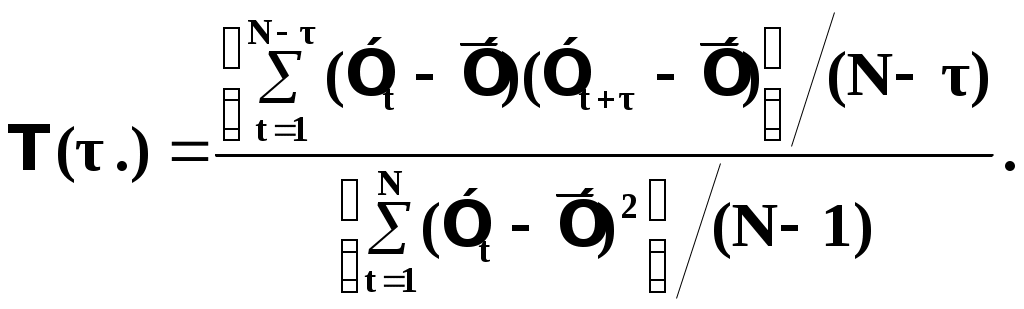 (4.5)График T() при =var называется коррелограммой, т.е. это выборочная оценка автокорреляционной функции. Обычно берут N/4 или N4. 4.6. Частный коэффициент автокорреляции. Частный коэффициент автокорреляции есть числовая мера корреляционной связи между Уt и Уt+ при условии устранения (элиминирования) влияния промежуточных членов между Уt и Уt+ 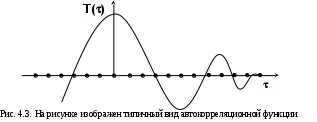 Свойства: 1). T()=T (-) – следствие эргодичности. 2). Наличие отрицательных значений T() говорит о наличие колебательных процессов в Y(t). 3). T() – затухает (ослабивается последствием) , т.е. амплитуда T() затухает по мере увеличения лагового сдвига . 4.7. Сглаживание временных рядов Сглаживание временных рядов: При сильном зашумлении базы данных перед идентификацией ВВ?. Предварительный анализ временных рядов: Предварительный анализ временных рядов обычно содержит три операции: сглаживание временных рядов; выявление и устранение аномальных наблюдений; выявление временного тренда. Целью этой операции является элеминирование (ослабление) случайной составляющей временных рядов по отношению к трендовой составляющей. Особенно полезно делать сглаживание временных рядов в качестве предпроцессорной обработки данных пред построением уравнением регрессии, аппроксимирующего тренд во временных рядах. В сложных условиях моделирования (сильное зашумление данных, отягощенные дефицитом наблюдения) предварительное сглаживание временных рядов за частую позволяет адекватно регрессивную модель превратить в достаточно адекватную. Этому также способствует отбраковка аномальных наблюдений и более «мягких» подходящих к оценки адекватности (снижения доверительной вероятности, на пример, до уровня 0,85… 0,9, если это позволяет постановка задачи). В эконометрике применяются методы сглаживания: Метод простой скользящей средней; Метод взвешенной скользящей средней; Метод эксионециального сглаживания и д.р. Наиболее простой и распространенный метод простой скользящей средней (МПСС). Алгоритм этого метода задается формулой: 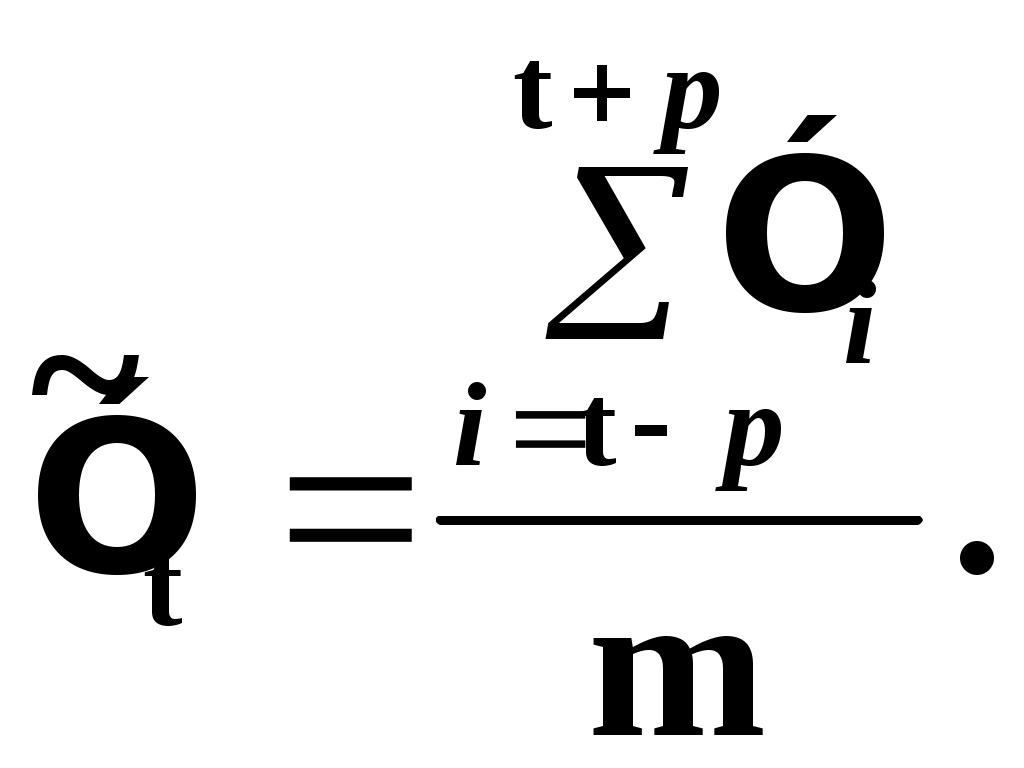 (4.6)где  – сглаженные значения уравнения временных рядов;  – текущие не сглаженные значения уравнения временных рядов;m – количество точек в интервале сглаживания; р – вспомогательный параметр (при нечетном m – р=(m-1)/2); i– индекс суммирования; t – текущий момент времени наблюдения во временном ряде. 4.8. Авторегрессионные модели. 1. Назначение: 1). Случай, когда для обычной регрессии нарушаются предпосылки регрессионного анализа. гетероскедантичность; автокоррелированность остатков; Переход к авторегрессии может значительно улучшить ситуацию. 2). Хорошо описывает колебательные процессы, на пример сезонные колебания. В моделях авторегрессии вместо регрессора t выступают лаговые переменные Лаговые переменные – это переменные, объясняющие моделирующую величину Y с некоторым запаздыванием. Второе отличие от классических временных рядов – то, что объясняющие переменные – случайные величины (по своему смыслу). AR(p) – порядка p.  . (4.7)т.е.  - есть линейная комбинация значений Y в предыдущие моменты времени; Здесь Y(t-1),….Y(t-p) – лаговые независимые переменные (переменные с запаздыванием); AR(1) – это Марковский случайный процесс (зависимость только от скорости - первых разностей):  (4.8)Пример:  4.9. Авторегрессионная модель скользящей средней. «Moving average» - скользящая средняя. ARMA - авторегрессионная модель скользящей средней. Замечание: Не следует путать авторегрессионную модель скользящей средней с методом простой скользящей средней при сглаживании временных рядов. В правой части этой модели стоят лаговые переменные по Y и e:  (4.9)4.10. Разностные уравнения с лаговыми пременными 1) Назначение: Если классическое уравнение регрессии (УР) оказалось неадекватным (например, имеет место смешенность остатков M[ei]0, их автокорреляция, гетероскедантичность), то целесообразно построение разностной авторегрессионной модели. 2) Структура уравнения регрессии: В левой части уравнения регрессии стоит аппроксимируемая величина Z(d) – разность порядка d, а в правой части линейная комбинация лаговых переменных порядка p, аппроксимирующая эту разность Z(d): 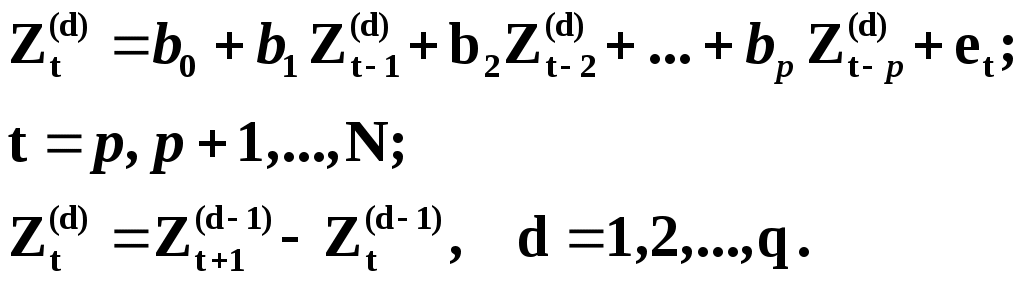 (4.10)Пример для разности первого порядка  Для практического построения разности автореррессионной модели необходимо провести идентификацию модели, т.е. выбрать оптимальные с точки зрения адекватности и качество модели значения порядка разности d* и порядка уравнения регрессии (числа лаговых переменных) р*. Может быть использован следующий алгоритм: 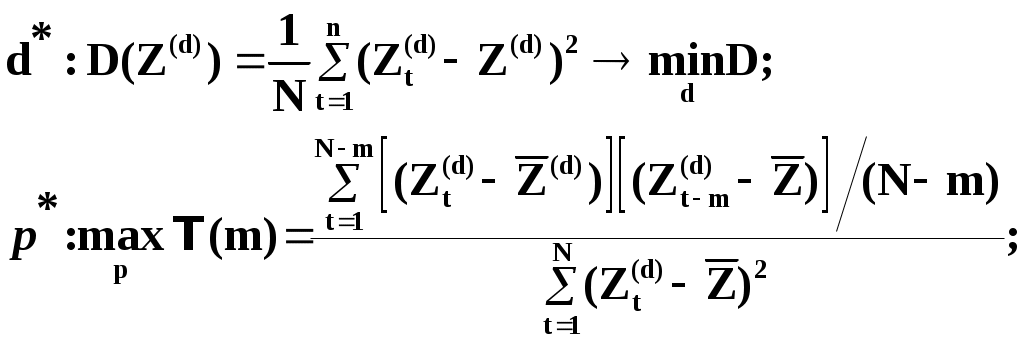 (4.11)4.11. Оценка коэффициентов регрессии. В структуру разностной авторегрессии – регрессии оцениваемые коэффициенты модели  входят линейным образом, поэтому применим классический метод наименьших квадратов: (4.12) - вектор наблюдений зависимой переменной.4.12. прогнозирование по разностной авторегрессионной модели. Прогнозирование осуществляется как в обычном линейном уравнении регрессии. После получения точечного и интервального прогноза следует вернуться от разностей к зависимой переменной Yt по формулам связи разностей с Yt. Например, для разностей первого порядка получим соотношение:  (4.13)Глава IV. Некоторые вопросы практического построения регрессионных моделей 5.1.Проблема спецификации переменных. Мультиколлинеарность Мультиколлениарность – это линейная взаимосвязь двух любых регрессоров Xj и Xk , (j, k =  ), что является нарушением 7 предпосылки метода наименьших квадратов.Здесь может быть два случая: а) Два любых фактора имеют между собой линейную функциональную (детерминированную) связь xj=a+bxk; (5.1) В этом случае соответствующий вектор столбцы базе данных xij, (  ) и xik, ( ) оказываются строго линейно – зависимыми и определитель матрицы нормальных уравнений равен нулю:  (5.2)Значит матрица  необратима и оценить параметры уравнения регрессии по методу наименьших квадратов невозможно. б) Линейная связь (5.1) стохастическая (скрытная). Однако она может быть выявлена путем вычисления коэффициента линейной парной корреляции  если критерии Стьюдента  значим, то стохастическая линейная взаимосвязь есть!Следствия: 1). Матрица нормальных уравнений формально обратима, но плохо обусловлена (её определитель  очень мал, и тем меньше, чем сильнее взаимосвязь хj и xk). При большей размерности этой матрицы (десятки и сотни регрессоров) возникают вычислительные проблемы.2) Если все же удалось построить уравнение регрессии с сохранением в нем мультиколлинеарных факторов, уравнение регрессии имеет плохое качество: Модель, как правило, неадекватна; Большие среднеквадратичные отклонения оцениваемых параметров  ;Оценки неустойчивы по вариации исходных данных; Данные моделирования трудноинтерпретируемы; 5.2.Способы устранения мультиколлинеарности 1) Выявление мультиколлинеарных пар, и их исключения (фильтрация регрессоров). Проводиться коэффициент автокорреляции, т.е вычисляется корреляционная матрица K. По критерию Стьюдента tT проверяется значимость её элементов {Tij}. В выявленных мултаколлинеарных – парах оставляется в модели тот регрессор, который теснее связан с Y, а другой отбрасывается. 2) Метод пошаговой регрессии 5.3. Метод пошаговой регрессии (конструктивный метод) Идея состоит в пошаговом алгоритме построения мультиколленеарных уравнений регрессии. При этом на каждом очередном шаге вводится еще одна независимая переменная. Для ЛУМР:  - одна объясненная переменная    – – – – – – – – – – – –  Процедура введения новых переменных продолжается до тех пор, пока будет (стабилизируется) скорректированный (адаптированный) коэффициент детерминации:  Заметим, что в данном алгоритме контроль отсутствия (или слабого проявления мультиколленеарности) реализуется косвенно. Если при введении нового регрессора скорректированный коэффициент детерминации  растет, причем  то это признак повышения качества модели. При наличии мультиколленеарности качество уравнения регрессии не улучшилось бы!5.4. Деструктивный подход (“расщепления”) мультиколлинеарных пар Алгоритм следующий: 1. Вводятся все регрессоры по итогам обработки экспертных оценок. 2. Проводится корреляционный анализ и вычисляется корреляционная матрица К. 3. Выявляются мультиколлинеарные пары, для которых критерий Стьюдента значим: 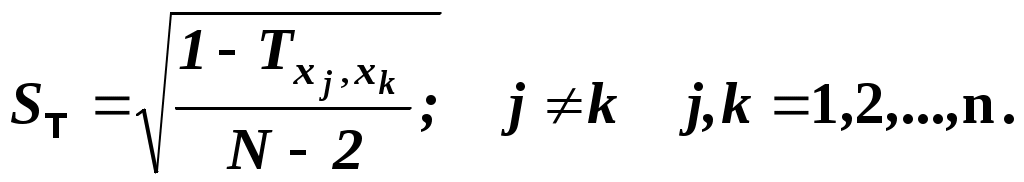  4. В модели оставляется та переменная из мультиколлинеарной пары  , которая теснее связана с Y, а другая отбрасывается.5.5.Случай нелинейных координатных функций 5.5.1.Формальная замена переменных Пусть  - нелинейные функции. Модель линейна по параметрам и нелинейна по . (5.3)Сделаем замену переменных 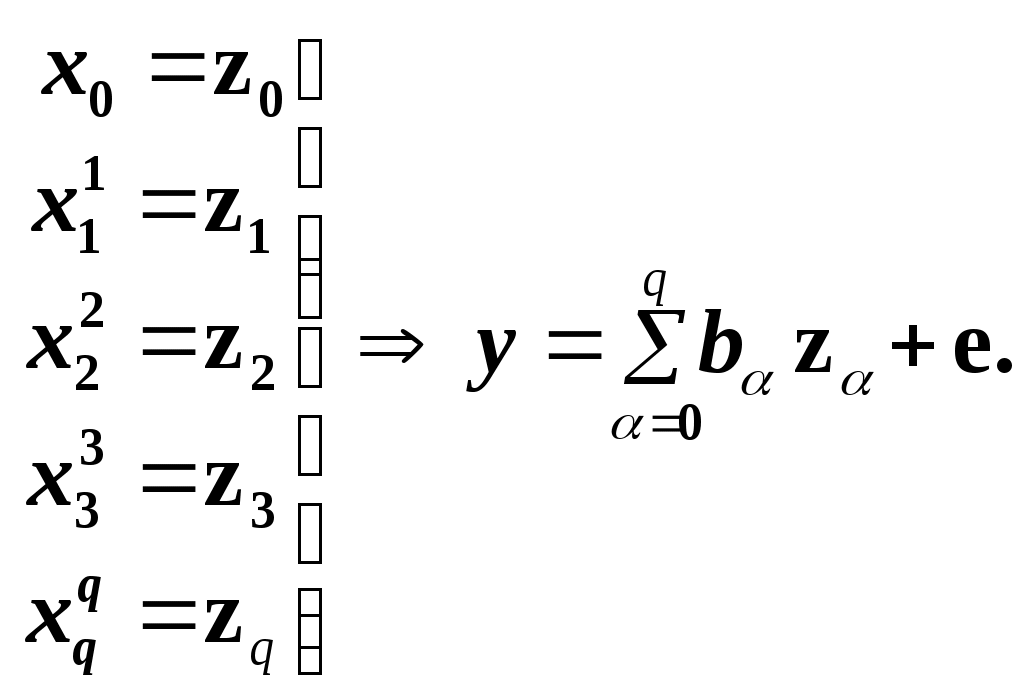 (5.4)Получаем исходный случай метода наименьших квадратов. После нахождения  , делается возврат к старым переменным.5.5.2. Специальное преобразование Пример:  Эта модель нелинейна, как по искомым параметрам, так и по входным факторам. Требуется уже не просто замена переменных, а специальное преобразование переменных.    5.6. Линейные уравнения регрессии с переменной структурой Фиктивные переменные При наличии качественных переменных имеем неоднородную структуру данных. а) Построение разных (отдельных) моделей для каждого уровня качественной переменной. б) Введение в уравнение регрессии качественных переменных. Они называются также фиктивными, номинальными, нечисловыми, структурными, “манекенами” (dummy variabls) и присвоение градациям этих переменных “цифровых меток”. Возможные подходы при кодировке: 1. Введение булевых (бинарных, дихотомических переменных)  Например: “признак 1” – есть высшее образование; “признак 2” – нет высшего образования. Случай нескольких градаций качественного признака. Если качественный признак имеет несколько уровней. Возможны два подхода: 1.Ввести дискретную переменную, имеющую столько же уровней, сколько признаков. 2.Ввести несколько бинарных переменных. В примере с образованием (начальное, среднее, высшее): Хj= (1; 2; 3;) Однако такие данные трудно содержательно интерпретировать. Действительно, приписываемые цифровые метки (1; 2; 3;) никак не связаны ни с экспертными оценками, ни с закономерностями исследуемого объекта. Такое кодирование вносит в уравнение регрессии искусственные связи. В частности, качественный признак “образование” может оказаться на порядок более значимым (или менее значимым) по сравнению с другими факторами в зависимости от цифр кода. Поэтому предпочтительнее способ 2, т.е. введение нескольких бинарных переменных. Правило: Число бинарных переменных должно быть на 1 меньше, чем число градаций качественного признака. Поясним это на примере с качественным признаком “образование”. Число градаций 3, значит достаточно ввести две бинарные переменные.   Если образование среднее, то автоматически оно не начальное. Если начальное, то это отражено парой {Z1=0; Z2=0}. Если ввести третью бинарную переменную  – возникает “логическая ловушка”.Если сумма значений фиктивный переменных, включенных в регрессию, равна постоянному числу (например: 1) в любой i–ой строке, то качественный признак будет неразличим в уравнение регрессии, т.е. его оценка будет смешана со свободным членом. Поясним это утверждение. Пусть качественный признак отражен тремя градациями и, соответственно закодирован тремя бинарными (двоичными) переменными Z1, Z2, Z3. Тогда их сумма равна: Zi = Z1+ Z2+ Z3 Z3=1 в любой i – ой строке матрицы планирования Х. Возникает функциональная мультиколлинеарность, т.е. мультиколлинеарность состоит в линейной зависимости первого столбца для  с вектор – столбцами для  , а именно: первый столбец равен сумме столбцов для качественных переменных. и метод наименьших квадратов неприменим. Сложные модели с влиянием качественных переменных на параметры :Замечание 3: Возможны смешанные уравнения регрессии с фиктивными переменными.  ( )Пример:  - потребление продукта.Х – доход Z1 – сезонность (влияние на свободный член) Z2 – уровень доходности домашнего хозяйства влияют на b1 при Х (склонность к потреблению). 5.7. Способ устранения коррелированности регрессоров с остатками с помощью инструментальных переменных Пусть имеется база данных  . Здесь Z – вектор инструментальных переменных. Пусть выявлена коррелированность  с остатками е. Уравнение регрессии дает несостоятельные оценки параметров . Причем  – это регрессоры, не коррелированные с остатками (инструментальные переменные).Идея метода инструментальных переменных: подобрать новые инструменты переменные , которые бы имели сильную корреляцию с  и не коррелировали с остатками е. При этом в качестве {  } могут выступать те регрессоры из числа { }, которые не коррелируют с E, а также другие величины. Обычно e > m, т.е. число компонент вектора больше , чем  . Например, в тесте Уайта при этих переменных коэффициент незначимы. Далее, исходные регрессоры аппроксимируются через инструментальные независимые переменные и тем самым “очищаются” от коррелированности с E . здесь применяется метод наименьших квадратов (первый шаг). Оценки получаются состоятельными. Переменные  , аппроксимированные линейными функциями от инструментальных переменных Zk называется очищенными (от коррелированности с остатками E) или новыми инструментальными переменными.В силу линейности всех связей можно связать полученные в итоге состоятельные оценки с Y через исходные регрессоры . Так мы приходим к алгоритму метода наименьших квадратов.5.8. Двух шаговый метод наименьших квадратов 1. Исходные (неочищенные) регрессоры xj аппроксимируются методом линейных уравнений регрессии от выбранных инструментальных переменных {Zk},  . ( )Получаем m ЛУМР, причем, независимых друг от друга (метод наименьших квадратов применяется m - раз). Для этого используется классический метод наименьших квадратов. Здесь {  } - матрица искомых коэффициентов; j - номер строки этой матрицы, равный номеру исходного регрессора xj; k – номер члена в ЛУМР, равный номеру инструментальной переменной Zk. Классический метод наименьших квадратов используется поочередно для каждого xj .Замечание. В силу некоррелированности инструмент. переменная Zk с остатками E эти оценки получаются состоятельными метода наименьших квадратов. 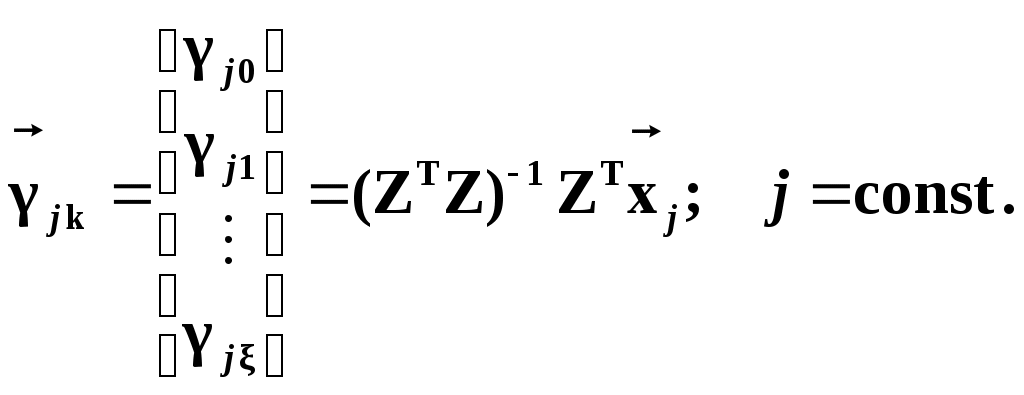 () ()N – число опытов; i – номер опыта; Z – матрица планирования эксперимента, где базисные функции – линейные функции от Zk.  Замечание: переменные не коррелируют с ошибками регрессии  , поскольку они выражаются в виде линейной комбинации некоррелирующих с E переменных {Zk}.2. Будем рассматривать { } как новые инструментальные переменные для Y и аппроксимируем Y через них.  ( )Вектор коэффициентов для каждой фиксированной компоненты 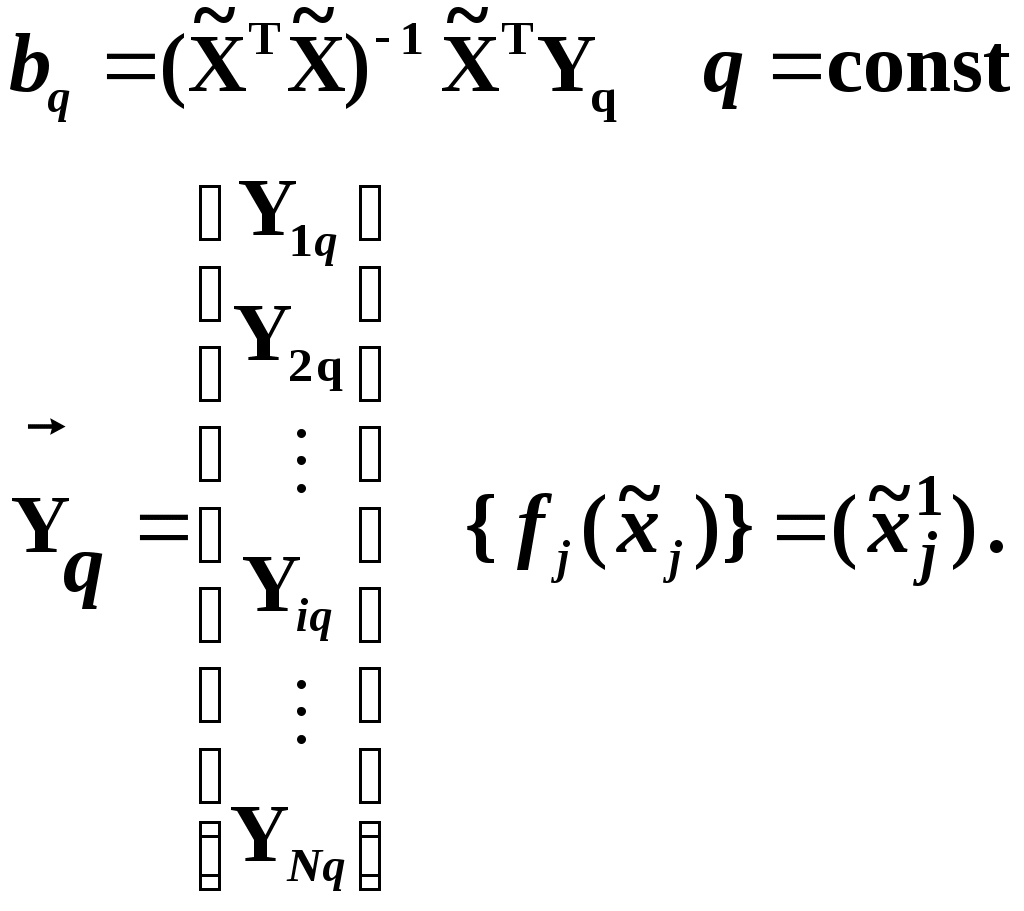 оцениваем снова с помощью классического метода наименьших квадратов: Всего получается таких l формул метода наименьших квадратов вида ( ); т.е.  ; где q - число исходных результативных переменных.3. Поскольку все преобразования линейны, то подставляя ( ) в ( ) получим выражение оценки двухшагового метода наименьших квадратов через исходные (а значит экономически интерпретируемые) инструменты переменной Zj  ( )Оценки [bjq]состоятельные Замечание: Для нелинейного МУР применимость 2х – шаговой процедуры сохраняется, однако связь  с получается уже численная.Вывод: Нужно сделать преобразования переменных перед применением 2х шагов метода наименьших квадратов Пример:  Вводим   Далее 2х –шаговую процедуру можно применять по стандартной схеме к ( ) Второй способ для систем одновременных уравнений (СОУ). Построить НСМ с числом нейронов в выходном слое, равном числу компонентов вектора 5.9. Обобщенный метод наименьших квадратов В обычном двух шаговом методе наименьших квадратов все компоненты Y1,…,Yq,…,Ye находятся по очереди, т.е. независимо. Качество оценки можно повысить, если данные обрабатывать совместно Пример: 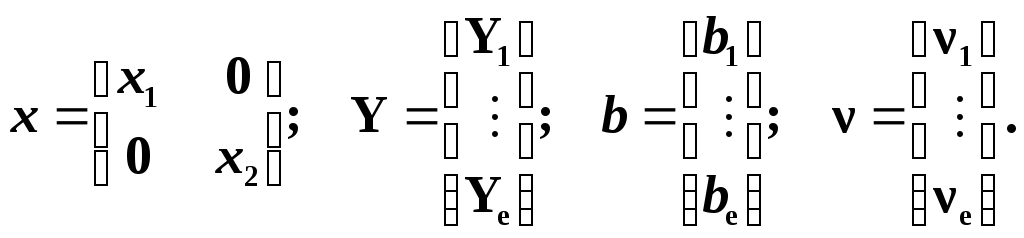 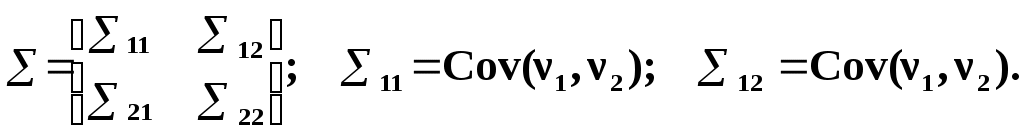;    где  - матрица ковариаций.Заметим, что если наборы регрессоров в обоих уравнений совпадают, то улучшения метода наименьших квадратов – оценок не происходит. Процедура одновременного оценивания (внешне не связанных уравнений), Seemingly Unreleased Regression (SUR), есть в западных экономических пакетах. 5.10. Трех шаговый метод наименьших квадратов 1.Вначале применяется обобщенный метод наименьших квадратов с целью устранения коррелированности для структурного уравнения ( ).  Затем к полученным “очищенным” уравнениям регрессии применяется 2-х шаговый метод наименьших квадратов. Замечание. Почти во всех пакетах есть 2-х и 3-х шаговые методы наименьших квадр Глава VI. Практическое применение (на примере разбора лабораторной и курсовой работы) Литература Айвазян С.А., Мхиторян В.С. Прикладная статистика и основы эконометрики: Учебник для ВУЗов. – М.: ЮНИТИ, 1998. Букаев Г.Н., Бублик Н.Д., Горбатков С.А., Сатаров Р.Ф. Модернизация системы налогового контроля на основе нейросетевых информационных технологий. – М.: Наука, 2001. Бублик Н.Д., Голичев Н.Н., Горбатков С.А., Смирнов А.В. Теоретические основы разработки технологии налогового контроля и управления. – Уфа: Изд. Башкирского государственного университета, 2004. Гринченко В.Т., Мацыпура В.Т., Снарский А.А. Введение в нелинейную динамику: Хаос и фракталы. Изд. 2-е. – М.: Изд. ЛКИ, 2007. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для ВУЗов/ Под ред. Проф. Н.Ш.Кремера. – М.: ЮНИТИ-ДАНА, 2002. Малинецкий Г.Г., Потапов А.Б., Подлазов А.В. Нелинейная динамика: Подходы, результаты, надежды. – М.:КомКнига, 2006. Орлов А.И. Эконометрика: Учебное пособие для ВУЗов. – М.:ЭКЗАМЕН, 2007. Перегудов Ф.Н, Тарасенко Ф.П. Введение в системный анализ: Учебное пособие для ВУЗов. – М.:Высшая школа, 1989. Петерс Э. Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка: Пер. с англ. – М: Мир, 2000. Прангишвили Н.В. Системный подход и общесистемные закономерности. – М.:СИНТЕГ, 2000. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. |