Учебники и учебные пособия по экономике ориентированы на студентов i высшего образования для которых читаются две отдельные дисциплины вначале Экономика математические методы и прикладные модели
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
|
Замечание 1: Всю теорию регрессионного анализа мы будем излагать для аддитивной формы (структуры) модели которая более наглядно интерпретируется: виден отдельный вклад каждого выходного фактора: В частном случае, когда в структуре модели на каждый входной фактор выделена одна базисная функция имеем: f(xj)fj(xj); j;q=n; f01. Пример: Здесь каждый член отражает вклад своего фактора, в общем случае нелинейный. Замечание: Вид координатных функций f(xj) выбирается в соответствии с особенностями моделируемого объекта. Это могут быть функции: степенные; показательные; экспотенциальные; логарифмические; тригонометрические и др. Для колебательных процессов, например сезонных колебаний, хорошо подходят гармонические функции. Удобно подбирать вид базисных функций f(xj) с помощью инструмента МS Excel «Мастер диаграмм». 3.2. Метод наименьших квадратов (МНК) в скалярной форме Используя уравнение регрессии (3.1), запишем функцию цели Ф, характеризующую качество аппроксимации объясненной части Ye=Mx(Y) уравнением регрессии: 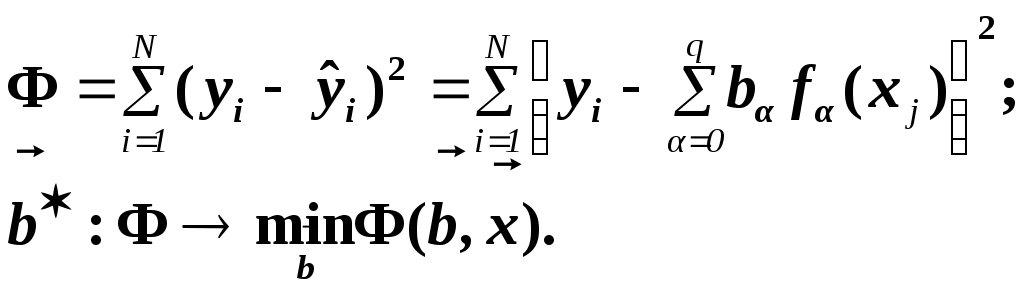 (3.2) (3.2)Это задача безусловной оптимизации, т.е требуется найти такие оптимальные значения Замечание: Для простоты далее считаем, что в уравнении регрессии каждый входной фактор xj предоставлен одним членом суммы со своей базисной функцией fj(xj), т.е. j. В теории регрессионного анализа показано, что функция Ф непрерывна и строго выпукла по аргументам bj. Тогда ее минимум обеспечивается условиям Система (3.3) называется системой, нормальных уравнений. Если вектор Замечание: Под линейным вхождением bj, в модель понимается, что сами координаторные функции fj(xj) могут быть нелинейными, но они не должны содержать ни одного оцениваемого параметра bj. Пример: Здесь обе модели нелинейны по независимой переменной х. Однако вторая модель линейна по искомому параметру b0 , в тоже время как в первой модели параметр b1 входит в структуру модели нелинейно. Если система нормальных уравнений, есть система линейных алгебраических уравнений, то для ее решения можно использовать аппарат линейной алгебры и, соответственно, матричную форму метода наименьших квадратов. 3.3. Матричная форма метода наименьших квадратов. 3.3.1.Уравнение наблюдений в матричной форме Запишем наблюдения в каждой точке i: Введем в рассмотрение матрицу плана наблюдений или матрицу базисных функций (не путать с вектором 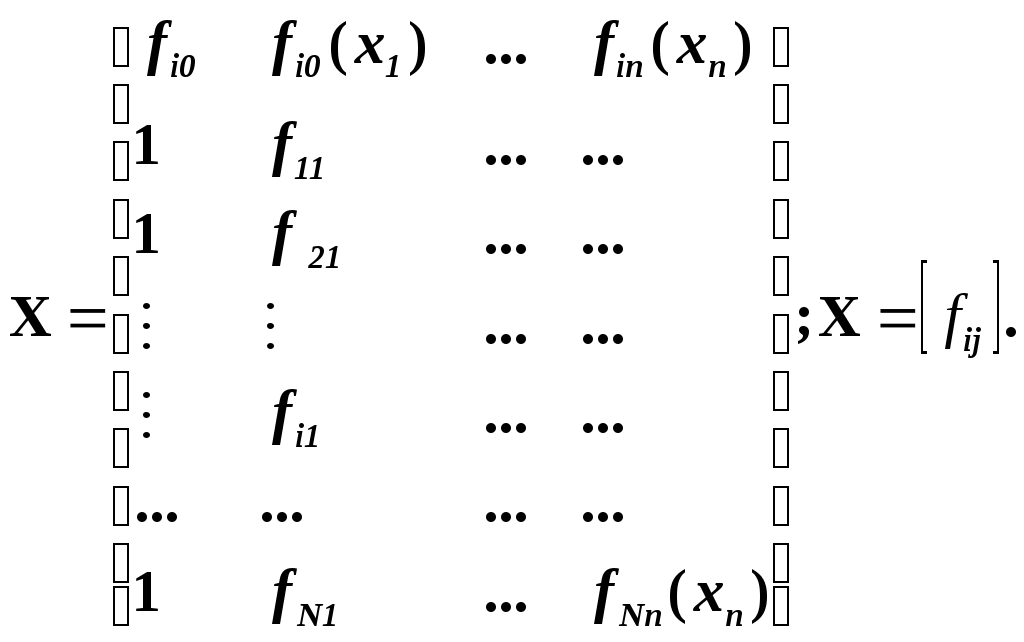 (3.5) (3.5)Тогда при условии линейного вхождения вектора параметров Справедливость уравнения (3.6) проверяется переводом уравнения (3.6) в скалярную форму по правилу умножения матрицы X на вектор В уравнении наблюдений (3.6) Замечание: Если структура модели нелинейна по 3.3.2.Нормальные уравнения регрессии и формула для параметров уравнения Используем известную формулу из матричной алгебры: Тогда, опуская стрелки с учетом того, что Система нормальных уравнений запишется в виде: где (XTX) – матрица нормальных уравнений. Пусть обратная матрица (XTX)-1 существует (она называется информационной матрицей Фишера). Тогда: В противном случае det(XTX)-1=0 и матрица нормальных уравнений необратима. Если det(XTX)-10, но очень мал, то обращаемая матрица плохо обусловлена. Возникает вычислительные проблемы обращения матриц большей размерности. 3.4. Предпосылки метода наименьших квадратов Классический метод наименьших квадратов, лежащий в основе регрессионного анализа, предъявляет довольно жесткие требования к базе данных и свойствам полученных случайных остатков: Должны выполняться ряд условий (предпосылки) метода наименьших квадратов. Пусть выполнена основная предпосылка эконометрического анализа, т.е. моделируемую случайную величину Y можно разбить на две части объясненную и случайную: Перечислим предпосылки классического метода наименьших квадратов. 1). Зависимая переменная Yi и возмущения Ei – это случайные величины, а вектор объясняющих переменных Хi – неслучайный (детерминированный). 2). Математическое ожидание возмущений Eiравно 0: MEi=0 3). Дисперсия возмущений Ei (дисперсия зависимой переменной Yi) постоянна: где Еn – матричная единица. Это условие называется гомоскедастичностью или равноизменчивостью возмущения Ei(зависимой переменной Yi). На рисунке 3.1. показан случай нарушения свойства гомоскедастичности: 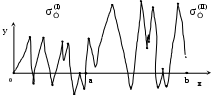 4). Возмущения Ei и Ej (или наблюдение Yi и Yj) не корректированы: M(EiEj)= 0 ; ij (3.13) 5). Ранг матрицы плана X[Nxn] должен быть не более числа опытов N: r=k < N, где, k – число членов регрессии. Ранг r равен числу линейно независимых столбцов матрицы X. 6). Возмущения Ei (или зависимая переменная Yi) есть нормально распределенная случайная величина EN(0;2En). (3.14) При выполнении всех предпосылок 1…5 и 6 модель называется классической нормальной регрессионной моделью. Замечание 1: Формально уравнение регрессии можно построить и без предпосылки о нормальном ЗР? возмущений Ei. Однако при этом модель не имеет практического смысла, поскольку невозможно оценить: адекватность; точность; доверительные интервалы оценок коэффициентов и Y. В этих операциях используется НЗР ? (критерий Стьюдента) Замечание 2: Для получения адекватного, хорошего интерпретируемого (с возможностью раздельной оценки вклада каждого фактора) уравнения регрессии с необходимой точностью требуется выполнение еще одной седьмой предпосылки. 7). Отсутствие мультиколлинеарности. Мультиколлениарность – это наличие линейной корреляции объясняющих переменных между собой. Предпосылки метода наименьших квадратов проверяются как соответствующие статистические гипотезы. 3.5. Свойства оценок, получаемых по методу наименьших квадратов Утверждение: Оценка 1). Она несмещенная (не содержит систематических ошибок) (Mbj= j), j= 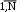 . (3.15) . (3.15)2). Оценка метода наименьших квадратов – состоятельная Здесь - сколько угодно малое число. Другими словами, при увеличении N оценка вектора 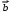 становиться все более точной, приближаясь к генеральному значению по вероятности. становиться все более точной, приближаясь к генеральному значению по вероятности.Заметим, что без этого свойства организация эксперимента была бы затруднительной. 3). Эффективность оценки (теорема Гаусса-Маркова). Если уравнение регрессии – это классическое нормальное линейное регрессии, т.е. удовлетворяются все предпосылки регрессионного анализа, то в классе линейных несмещенных оценок метода наименьших квадратов – оценка 3.6. Оценка адекватности уравнения регрессии (проверка гипотез о предпосылках метода наименьших квадратов) 3.6.1.Гипотеза о близости к нулю математического ожидания остатков Здесь используется критерий Стьюдента для остатков и проверяется нуль-гипотеза: S - среднее квадратичное отклонение остатков – мера рассеяния остатков относительно своего среднего 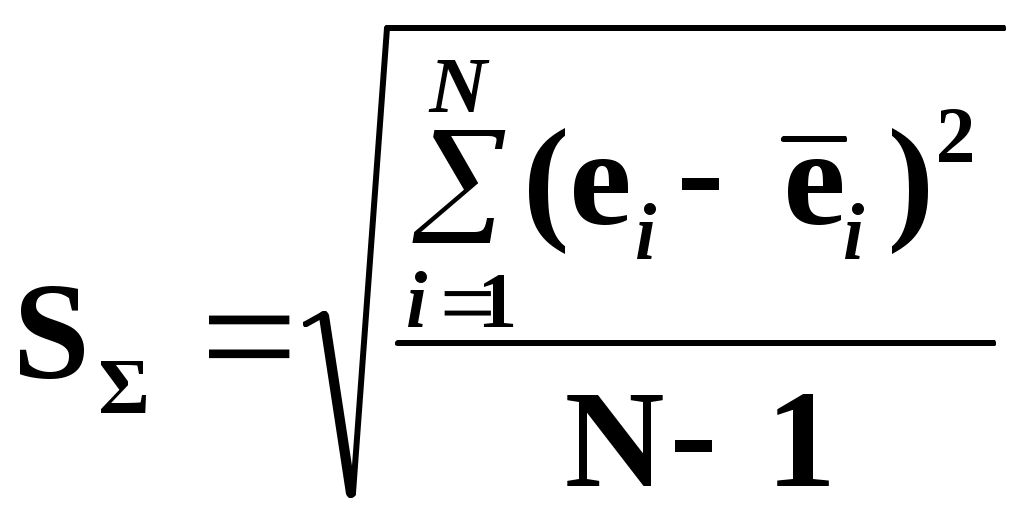 (3.18) (3.18)Замечание: Здесь число степеней свободы S=(N – 1), так как на вычисление среднего (центра рассеяния) расходуется одна степень свободы: 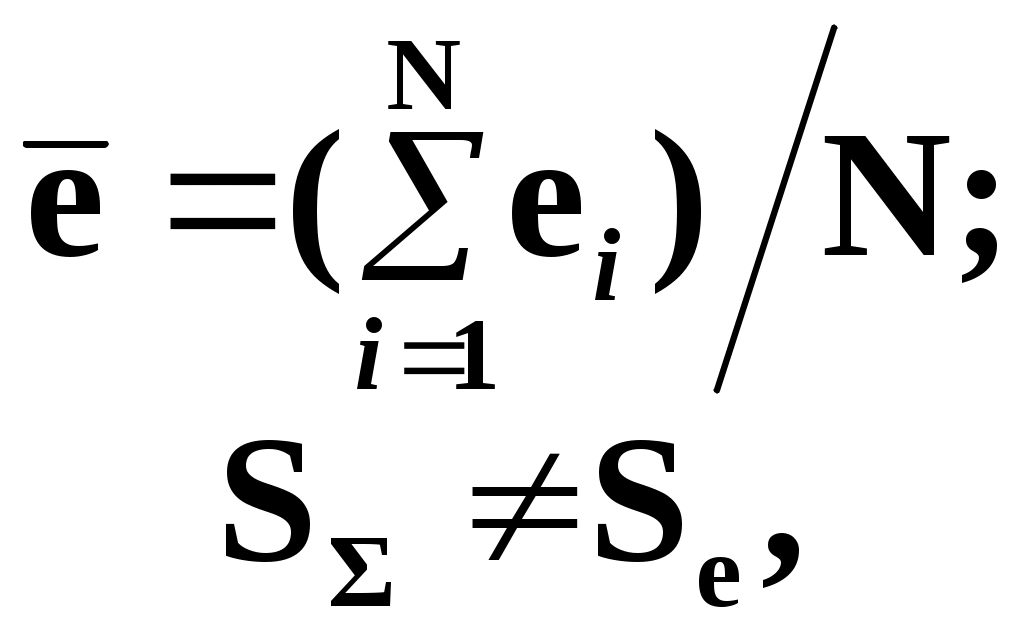 (3.19) (3.19)где Se- среднее квадратичное отклонение наблюдений Yi относительно поверхности регрессии 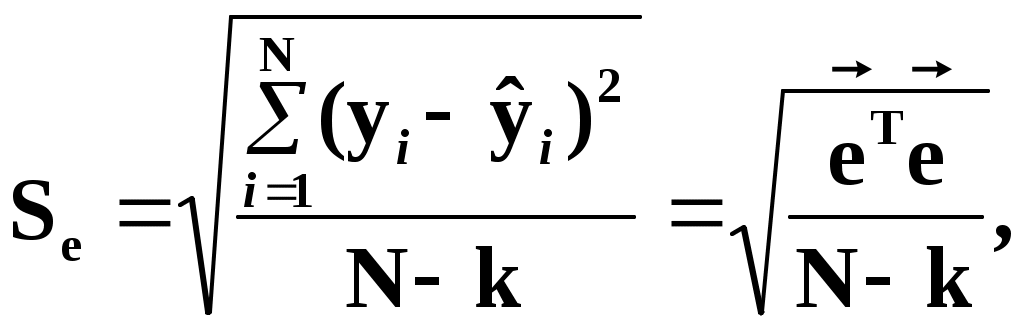 (3.20) (3.20)где, k – число членов уравнения регрессии, включая свободный член. 3.6.2. Гипотеза о статистической значимости коэффициентов регрессии bj Используя t – критерий Стьюдента проверяем нуль гипотезу: 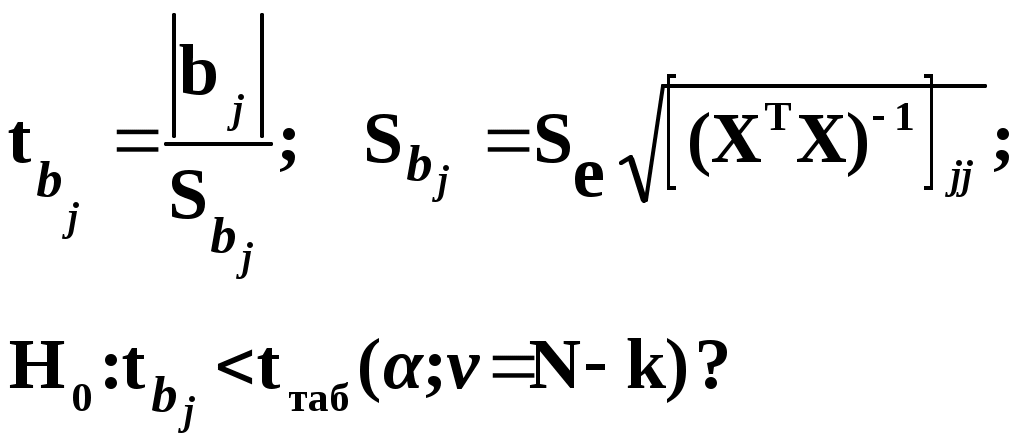 (3.21) (3.21)Выводы: Если данное неравенство выполнено, то коэффициент bj – статистически не значим. Если все коэффициенты в уравнение регрессии не значимы то уравнение регрессии не значимо: влияние регрессоров Хj на формирование значений Y не различимо на фоне случайных возмущений E. Модель не адекватна. Если все коэффициенты уравнения регрессии значимы, то нарушение адекватности в данном пункте (по данной гипотезе) нет. Но вывод об адекватности делать рано, должны быть выполнены все предпосылки метода наименьших квадратов. Если часть коэффициентов уравнения регрессии значима, а часть не значима, то это не является снованием для нарушения адекватности. Значимая часть регрессоров может адекватно описывать объект. Незначимые коэффициенты уравнения регрессии и соответствующие им регрессоры следует исключить из модели: они не несут никакой полезной информации. 3.6.3. Гипотеза о статистической значимости всего уравнения регрессии в целом Используется критерий Фишера- Снедекора F и проверяется нуль-гипотеза: 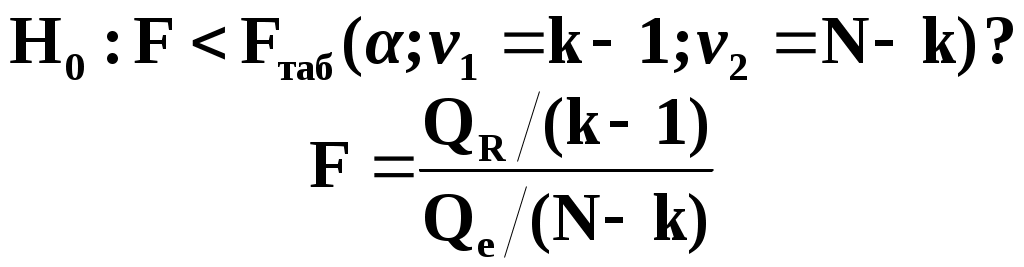 (3.22) (3.22)QR – сумма квадратов отклонений расчетных значений Выводы: 1. Если гипотеза Н0 выполнена, то уравнение регрессии в целом статистически незначимо и можно сразу делать вывод о неадекватности модели. 2. Если нуль-гипотеза Н0 не выполнена, т.е. F>Fтаб, то уравнение регрессии в целом значимо и можно переходить к проверке других гипотез. 3.6.4. Оценка качества уравнения регрессии Для комплексной оценки качества уравнения регрессии используется коэффициент детерминации R2 Коэффициент детерминации R2 как мера качества уравнения регрессии характеризует долю вариации зависимой переменной, обусловленную регрессией (влиянием факторов), в общей вариацией результативной переменной Yi ; чем ближе коэффициент детерминации R2 к единице, тем лучше уравнение регрессии аппроксимирует экспериментальные данные, тем ближе эмпирические точки располагаются к линии регрессии, тем больше прогностическая сила модели. Замечание: Коэффициент множественной детерминации, определяется по результатам линейного корреляционного анализа, не следует смешивать с рассматриваемым коэффициентом детерминации R2, справедливого и для моделей, нелинейных по регрессорам (в этом случае его следует называть «индексом множественной детерминации»). Другими словами, R2Rj.12…m2. Это разные коэффициенты: первый из них связан с регрессионным анализом, т.е. привязан к конкретной параметрической модели 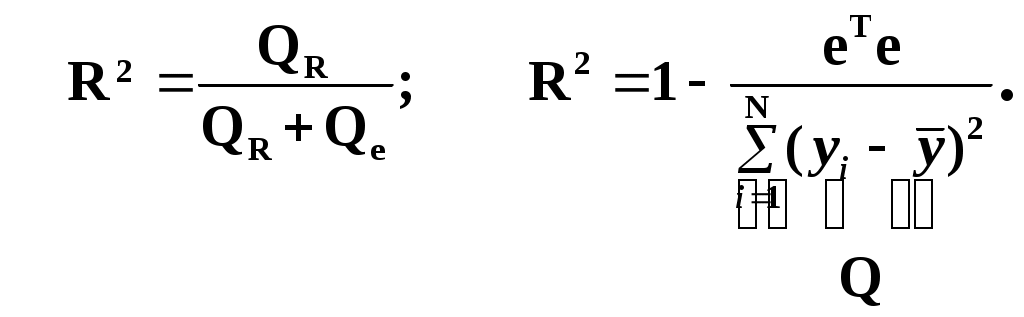 (3.23) (3.23)Последняя формула справедлива только для линейных корреляционных связей. Приемы улучшения качества модели: 1). Сделать предварительное сглаживание временного ряда одномерного или многомерного по методу простой скользящей средней или экспоненциального сглаживания. Данный прием применяют только при наличии упорядочного наблюдения во времени, т.е. для использования данных пространственного типа он не применяется. 2). Использовать нормирование всех переменных и зависимых и независимых: 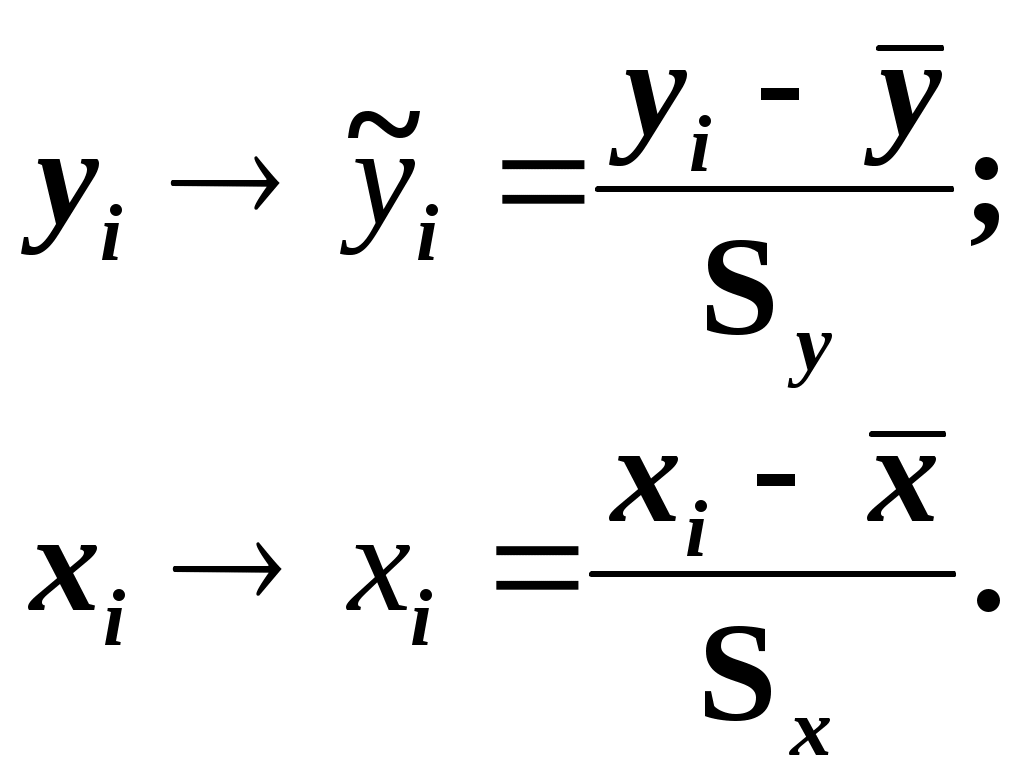 (3.25) (3.25)Выводы: 1. Приемлемость получаемого значения R2 определяется целями моделирования: если допустимы грубые (прикидочные) оценки, то можно принять R2 0,8, для более точных оценок R2 > 0,9. 2. Если база данных (БД) сильно зашумлена (или даже сознательно искажена, что имеет место в задачах налогового и финансового контроля), то может оказаться, что никакие ухищрения (о них речь позже) не позволяют получить R2>0,9. Что делать тогда? Рекомендации: Повысить информативность базы данных за счет различных алгоритмов предпроцессорной обработки (сглаживание, если база данных упорядочена по времени; кластеризации данных; компрессия данных (факторный анализ); расширения бахзы данных как парирование ее зашумленности; накнец – переход к другим моделям: нейросетевым нечетким; фрактальным. 3.6.5. Скорректированный коэффициент детерминации Недостаток нескорректированного коэффициента детерминации в том, что R2 увеличивается при введении новых факторов, хотя качество уравнения регрессии может и не возрастать, т.е. вводимые регрессоры оказываются малозначимыми. Скорректированный (адаптивный) коэффициент множественной детерминации определяется по формуле: В отличие от не скорректированного коэффициента детерминации R2 этот коэффициент может в принципе уменьшается при увеличении числа регрессоров (за счет знаменателя второго члена), если эти дополнительные регрессоры малозначимы, т.е. 3.6.6. Проверка гипотезы о чисто случайном характере остатков Здесь может быть два случая: Случай а): База данных упорядочена по времени: вектор – строки (или кортежи ti=t1,t2,…..tn; tn>ti-1 , i= В этом случае можно применить для оценки чисто случайного характера остатков е два критерия: поворотных точек, либо критерий Фостера- Стьюарта (отсутствие тренда в остатках). Критерий Дарбина – Уотсона (отсутствие автокорреляции в остатках) 1) При проверке гипотезы об отсутствии временного тренда в остатках по критерию поворотных точек проверяется нуль гипотеза: 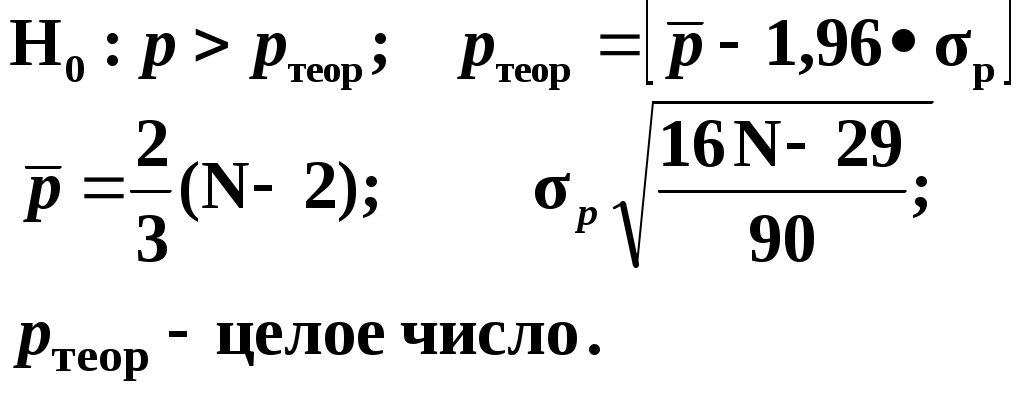 (3.27) (3.27)Если неравенство истинно, т.е. экспериментальное число поворотных точек p, определяемое по графику, меньше теоретического, то означает что имеется тренд в остатках и остатки не являются чисто случайными. Если неравенство нарушено, то тренда в остатках нет, и их можно считать случайными, как не содержащие тренда. 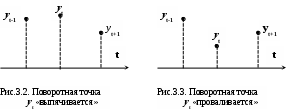 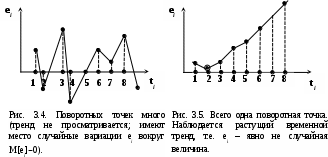 Если нуль-гипотеза Н0 выполняется, то временного тренда нет. 2. Проверка гипотезы о наличии автокорреляции в остатках по критерию Дарбина-Уотсона Автокорреляция – это корреляция между членами одного временного ряда. Здесь можно испльзовать d – статистику Дарбина-Уотсона: 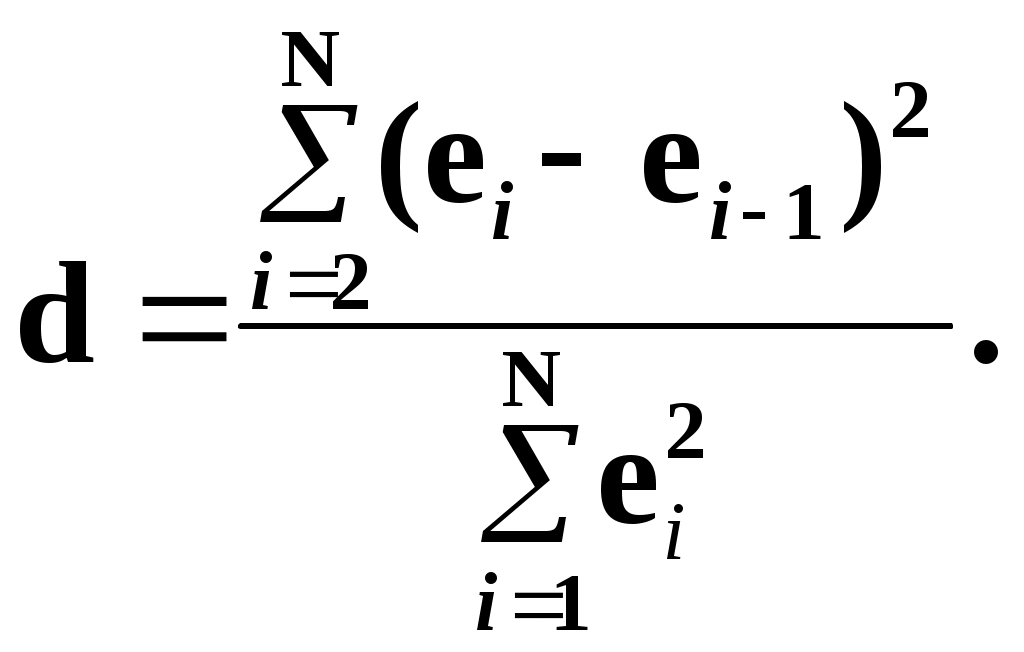 (3.28) (3.28)Смысл этого критерия: чем меньше разность суммируемых членов, тем сильнее проявления «последействия», т.е. влияния предыдущего остатка на последующий и тем вероятнее наличие автокорреляции остатков. Замечание: 1. Если d>2, то перед входом в таблицу теоретических значений d-критерия надо сделать преобразование переменных: dd = 4-d Выводы: Автокорреляция имеет место, остатки не являются чисто случайными, нарушена адекватность модели, если d < dтаб.min. Ничего сказать об автокорреляции енльзя, нужно использовать другие критерии, если d dтаб.min; dтаб.max. Автокорреляция отсутствует, нарушений адекватности нет, если d > dтаб.max. При не определенной ситуации применяются другие критерии. В частности, можно использовать первый коэффициент автокорреляции, т.е. коэффициент линейной парной корреляции между соседними членами временного ряда еt, еt-1: 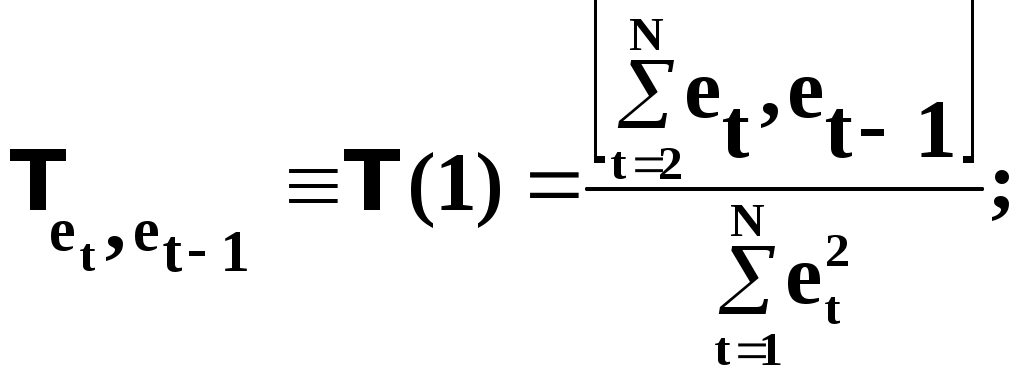 (3.29) (3.29)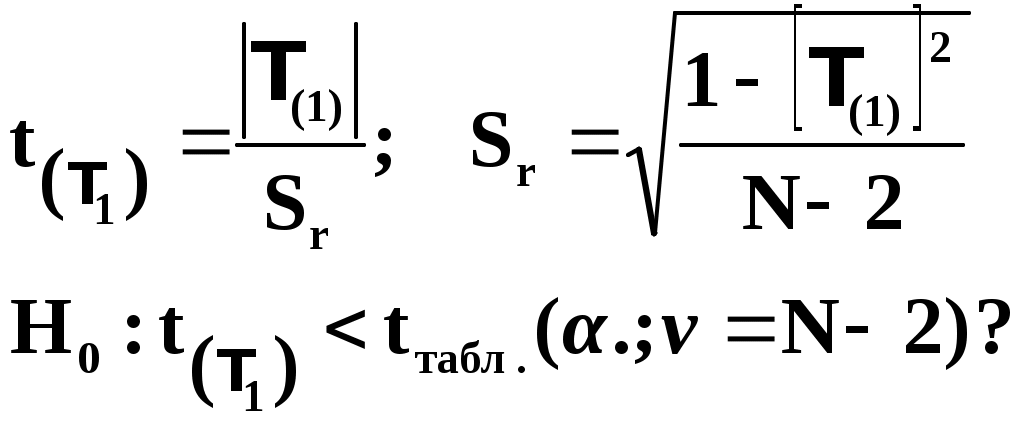 (3.30) (3.30)Случай б): База данных не упорядочена во времени (например, при социологических опросах, данные по разным странам т.д.) В этих случаях упомянутые выше критерии поворотных точек, Фостера- Стьюарта, Дарбина- Уотсона в принципе неприменимы. Вместо них проверяется тест на отсутствие гетероскедастичности, т.е. корреляции между регрессорами Тест Уайта: строится линейное уравнение регрессии для квадратов остатков: 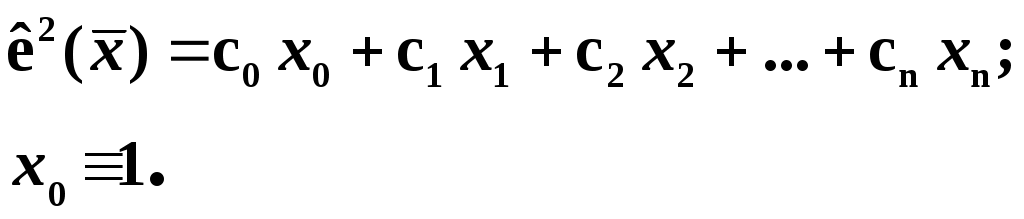 (3.31) (3.31)Гипотеза о статистической значимости линейного уравнения регрессии для квадратов остатков в целом проверяется по критерию Фишера-Стьюдента, точно так же как и для основного уравнения регрессии. 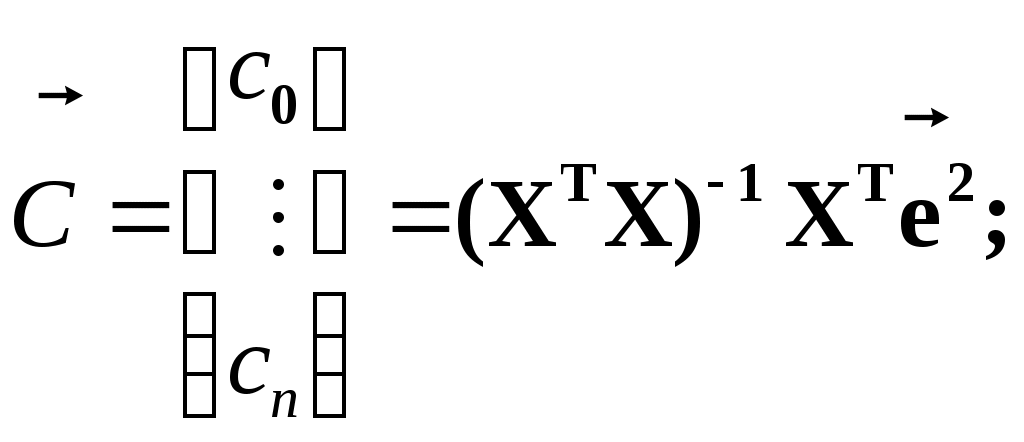 (3.32) (3.32)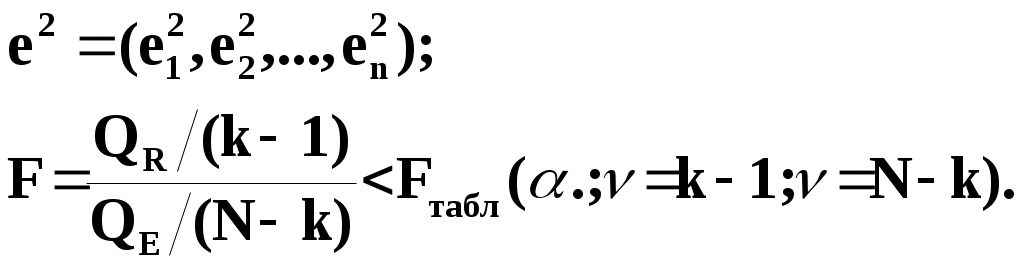 (3.33) (3.33)Вывод: Если нуль-гипотеза для критерия Фишера выполняется, то гетероскедастичности нет Если неравенство не выполняется, то это означает что гетероскедастичность есть. 3.6.7. Проверка гипотезы о нормальном законе распределения остатков Используется (R/S) - критерий, т.е. нормированный размах остатков: (R/S) = (еmax-еmin)/Se, (3.34) где Se определяется формулой (3.20). Вывод: Если В противном случае – отвергается. Общий вывод: Если все 6 гипотез, рассмотренные выше, о предпосылках метода наименьших квадратов выполняются и критерии качества модели R2 приемлемы для поставленных целей моделирования, то модель считается адекватной и пригодна для практического применения. Замечание. Если выборка деформируется (сужается или расширяется) либо изменяется принимаемый уровень значимости оценок, то проверку адекватности надо делать заново. 3.7. Точечный прогноз и оценка доверительных интервалов прогноза Найдем средние квадратические отклонения, которые потребуются нам при получении полуширины доверительных интервалов прогноза для: коэффициентов регрессии расчетного значения моделируемой величины индивидуальных значений случайной величины Y 1) Среднее квадратичное отклонение фактических наблюдений где k – число членов в уравнении регрессии; 2) Среднее квадратическое отклонение для случайных величин – коэффициентов регрессии: Здесь 3) Среднее квадратическое отклонение расчетного значения где 4) Среднее квадратическое отклонение для индивидуальных значений 5) Полуширина доверительного интервала 6) Полуширина доверительного интервала 7) Полуширина доверительного интерваладля разброса индивидуальных значений Y: 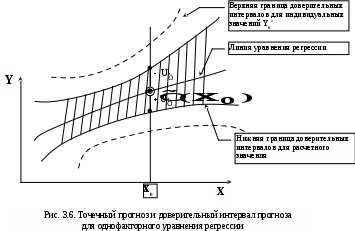 3.8. Оценка погрешностей расчета по уравнению регрессии Традиционно используются две числовые меры для оценки погрешностей расчета: Среднеквадратическая ошибка Se по формуле (3.35). Средняя по модулю ошибка. Замечание: Числовые меры ошибок расчета Se по (3.35) и Идея ретроспективного анализа заключается в следующем. Пусть имеется многомерная выборка из N наблюдений, упорядоченных во времени. При оценке вектора параметров Получим оценки погрешности: среднеквадратичную 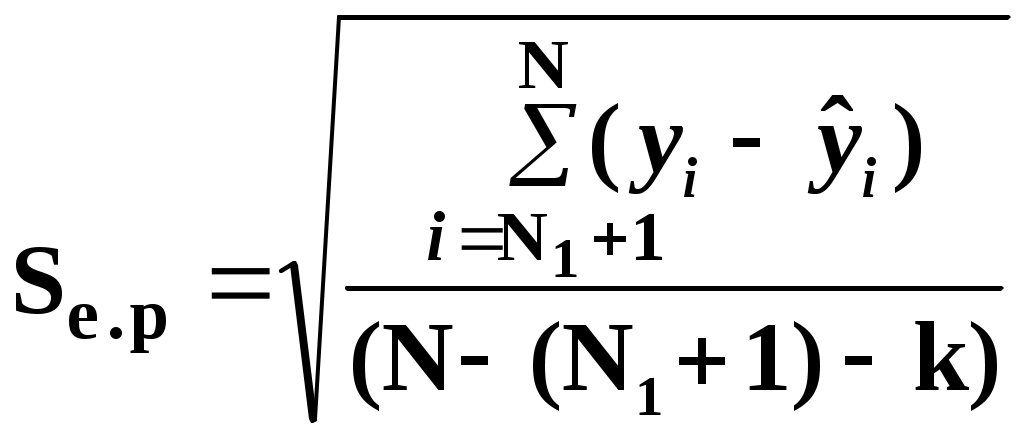 (3.43) (3.43)среднюю по модулю 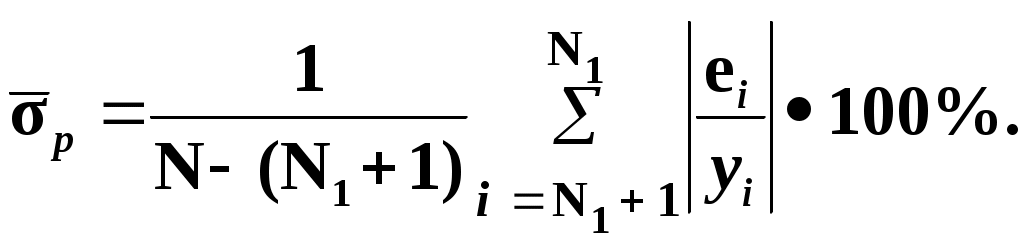 (3.44) (3.44)3.9. Коэффициент эластичности, бета-коэффициент и дельта-коэффициент для линейного уравнения регрессии 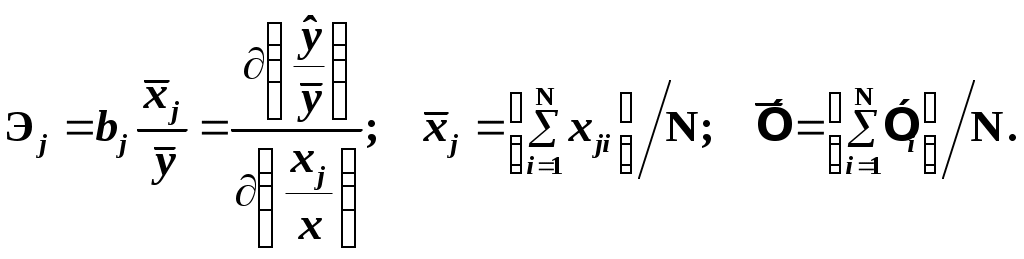 (3.45) (3.45)j - номер объясняющей переменной; Коэффициент эластичности показывает: на сколько единиц (либо процентов) в долях от среднего значения Таким образом, Эj измеряет чувствительность Замечание. В учебниках по эконометрике почему-то умалчивается вопрос: в долях от чего измеряются вариации Бета-коэффициент выражается формулой Это 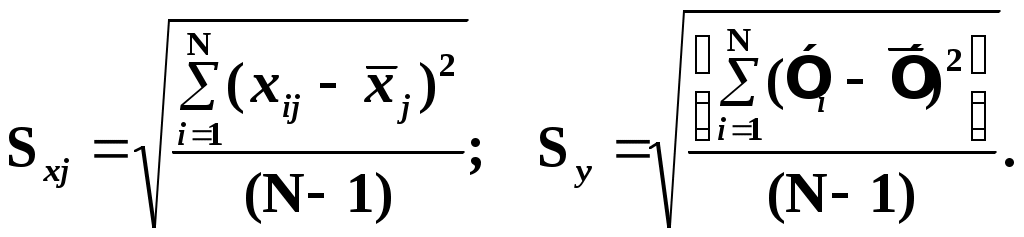 (3.47) (3.47)Дельта-коэффициент определяется по формуле Здесь Дельта-коэффициент показывает долю влияния каждого фактора в суммарном влиянии всех факторов на зависимую переменную Y. |
