Учебники и учебные пособия по экономике ориентированы на студентов i высшего образования для которых читаются две отдельные дисциплины вначале Экономика математические методы и прикладные модели

• Название: Учебники и учебные пособия по экономике ориентированы на студентов i высшего образования для которых читаются две отдельные дисциплины вначале Экономика математические методы и прикладные модели
• Дата: 16.05.2022
• Размер: 1.1 Mb.
• Имя файла: 938b1d3.doc
• Тип: Учебники и учебные пособия; #533199
• страница: 2 из 4

Глава II. Корреляционный анализ
2.1. Цель корреляционного анализа
Цель корреляционного анализа – количественная оценка тесноты связи между случайными величинами.
2.2. Числовые меры корреляционной связи
2.2.1. Ковариация
Приставка «Ко» означает «совместный» (ковариация – взаимосвязанная или совместная вариация). Генеральное значение ковариации определяется формулой:
(2.1)
Здесь М - оператор вычисления математического ожидания, нуль вверху означает центрирование величины.

Заметим что в формуле (2.1) вариация случайных величин Y и X измеряется их отклонением от математических ожиданий, а условие «совместности» измерения вариаций реализуется операцией умножения внутри квадратных скобок.
2.2.2. Выборочная оценка коэффициента линейной парной корреляции
На практике вместо генеральной совокупности мы имеем выборку из неё. Будем считать выборку репрезентативной, а связь между случайными величинами Y и X – линейной:
y = ₀ +₁x, (2.2)
где ₀, ₁ – генеральные (теоретические) значения параметров линейного уравнения регрессии (2.2.), которые будем обозначать греческими буквами, а их выборочные оценки ₀, ₁ – латинскими малыми буквами.

Если нормировать ковариацию (2.1), т.е. разделить ее на произведение средних квадратических отклонений (СКО) и , то получим коэффициент парной корреляции. Генеральное значение коэффициента равно:
(2.3.)
а выборочная оценка: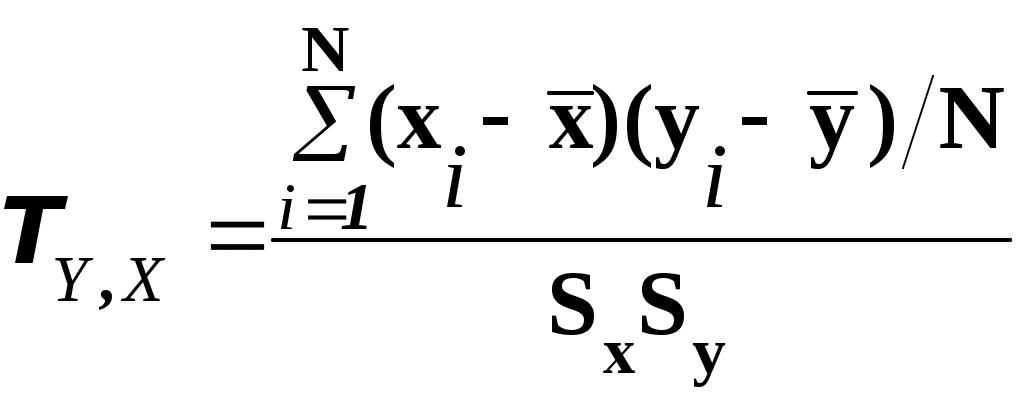
(2.4.)
- выборочные оценки математических ожиданий m_x, m_y;

S_x,S_y – выборочные СКО.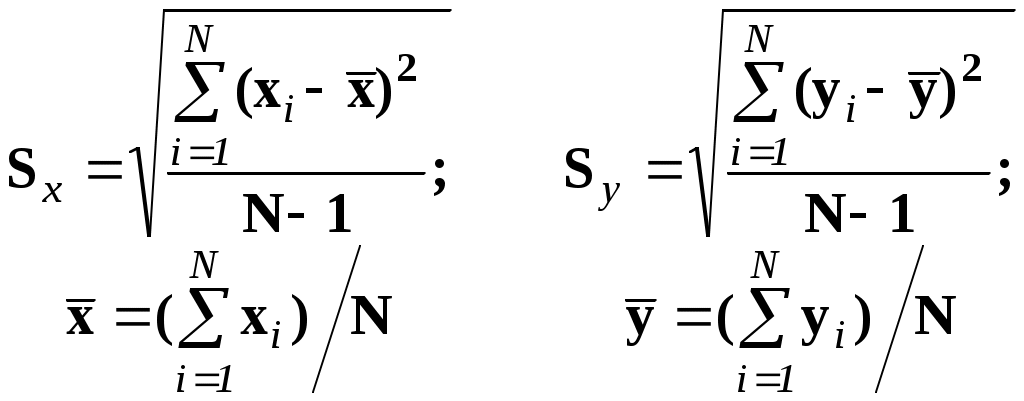

(2.5)
Знак при T определяет форму (характер) корреляционной связи в уравнении (2.2):
(+) положительный знак соответствует возрастающему виду (при росте случайной величины х другая случайная величина тоже работает в среднем);

( - ) отрицательный знак соответствует убывающему виду, зависимости (2.2).
Таким образом коэффициент линейной парной корреляции изменяется в пределах .
2.2.3. Математический смысл коэффициента линейной парной корреляции
Предположим, что между двумя случайными величинами X и Y в среднем существует линейная связь (2.2), т.е. они связаны линейным уравнением регрессии для математических ожиданий
(2.6)
При взгляде на уравнение регрессии видно, что измерителем связи Y и X может служить коэффициент b₁. Действительно, вычисляя производную от функции , получим:

т.е. b₁ оценивает скорость изменения функции Y при изменении аргумента X. Однако b₁ неудобен как измеритель связи тем, что b₁ зависит от единиц измерения X и Y. Хотелось бы иметь безразмерный показатель. Сделаем это, переходя к нормированным переменным в уравнении регрессии: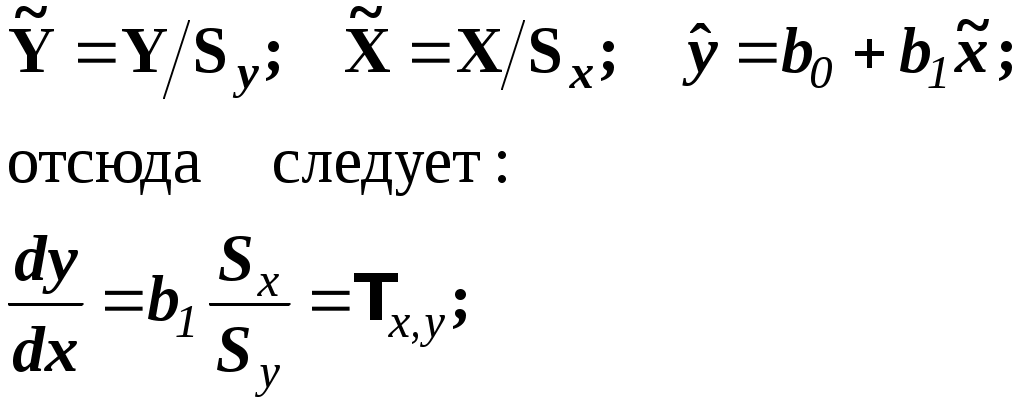
(2.7)
Коэффициент корреляции T_x,y есть скорость изменения (производная) нормированной функции при вариации нормированного аргумента и линейной связи между ними.

2.2.4. Статистический смысл коэффициента линейной парной корреляции
Запишем производную в приращениях:
(2.8)

Заметим, что здесь – это так называемый в регрессионном анализе бэтта-коэффициент [ ].

Коэффициент линейной парной корреляции показывает на сколько процентов (%)(в долях от СКО S_y) изменяется случайная величина Y, если другая величина X измениться на 1% в долях от своего СКО S_x.
2.2.5. Геометрическая интерпретация коэффициента корреляции
Геометрическую интерпретацию коэффициента линейной парной корреляции как измерителя силы связи между случайными величинами Y и X можно уяснить из рисунку 2.1.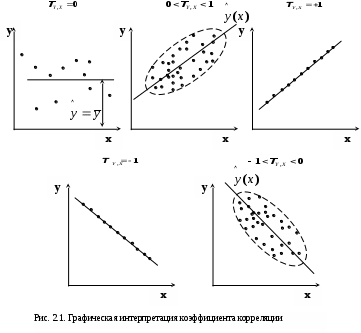

где:

а) – связь между Y и X в среднем отсутствует (коэффициент b₁ в (2.6) равен нулю);

б) – возрастающая (в среднем) статистическая зависимость Y от X (b₁>0);

в) – возрастающая детерминированная (функциональная) связь Y и X;

г) – падающая детерминированная (функциональная) зависимость;

д) – падающая статистическая зависимость.
2.3. Проверка статистической значимости коэффициента корреляции
Для проверки этой гипотезы используется критерий Стьюдента для статистики:

(2.9)
Критическое (табличное значение критерия Стьюдента определяется при выбранном уровне значимости  и числе степеней свободы .

Уровень значимости – это вероятность, с которой мы не гарантируем правильности статистических оценок. Соответственно, доверительная вероятность
(2.10)

Это вероятность, с которой мы гарантируем правильность этих оценок.

Величина  (либо p) задается «Заказчиком» расчетов, либо самим аналитиком, строящим модель, исходя из экономического смысла постановки задачи.
2.4. Множественный корреляционный анализ
Как правило экономический процесс описывается числом показателей, более двух, т.е. вектором случайных величин:
X=(X₁, X₂….., X_j…., X_m)
j- номер показателя (фактора)
2.4.1. Корреляционная матрица
Пусть совокупность Xj имеет совместный нормальный закон распределения. Тогда, как и ранее, взаимосвязь между двумя показателями Xi и Xj можно описать коэффициентом парной линейной корреляции Tij. Множество всех возможных сочетанийTij , i,j= 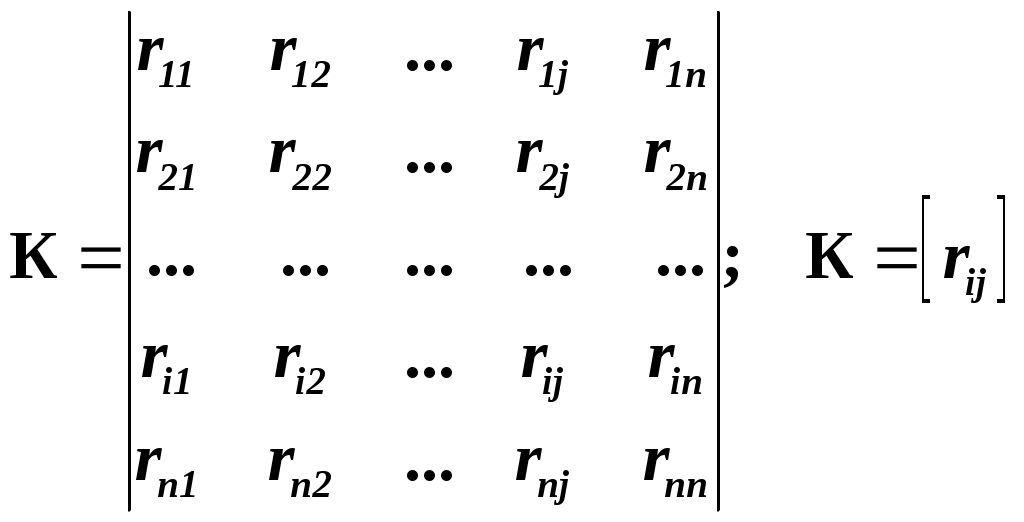образует квадратную корреляционную матрицу:

(2.11)
Отметим важные свойства корреляционной матрицы
1). Все диагональные элементы этой матрицы равны единице:
daig K = Tji = 1
2). Корреляционная матрица – симметричная, т.е. ее элементы, симметричные относительно главной диагонали, равны друг другу:

Tij = Tji,

так как произведение в формуле (2.4) для Tij не зависит от порядка следования сомножителей.
2.4.2. Выборочный коэффициент множественной корреляции
К оэффициент множественной корреляции определяет тесноту связи одного показателя с совокупностью остальных (n-1) показателей при их одновременном действии:.
(2.12)
Kjj – алгебраическое дополнение элемента Tjj матрицы К.

Коэффициент множественной корреляции изменяется от 0 до +1, т.е. всегда неотрицателен.
2.4.3. Частный коэффициент корреляции
Частный коэффициент корреляции служит количественной мерой связи случайных величин Xi и Xj при условии исключения влияния других случайных (m-2) величин, т.е. при их фиксации.

Выборочная оценка коэффициента частной корреляции определяется по формуле:
(2.13)
где Kij, Kjj – алгебраическое дополнение соответствующих элементов матрицы К.

Частный коэффициент корреляции так же, как и парный коэффициент линейной парной корреляции, изменяется от -1 до + 1, т.е. может быть отрицательным.

Гипотеза о значимости частного коэффициента корреляции проверяется так же, как и для парного коэффициента корреляции:
H₀ : t_r < t_таб(; N-2)?
2.4.4. Коэффициент детерминации
Коэффициент детерминации равен квадрату множественного коэффициента корреляции и показывает: какую долю общей дисперсии исследуемого показателя Xj объясняет (формирует) вариация всех остальных (n-1) показателей X₁,X₂,…,X_n при их совместном действии:
(2.14)

2.4.5. Оценка значимости множественного коэффициента детерминации
Используется F – статистика Фишера для R²:
(2.15)
где, m – число компонент вектора ; N – число опытов.

Проверяется нуль гипотеза:

H₀ : F = 0;

если то коэффициент множественной корреляции незначим (гипотеза Н₀ принимается);

если то R² значим (гипотеза Н₀ отвергается);

– ₁– число степеней свободы для числителя; ₂ – число степеней свободы для знаменателя (₁=m-1; ₂=N-m) дроби (2.15).
2.4.6. Индекс корреляции при нелинейной связи двух случайных величин
Слово «индекс» здесь понимается в смысле «отношения» [ ]. Поэтому употребляется и другой термин для этой числовой меры: «корреляционное отношение».

Пусть две случайные величины X и Y связаны в среднем нелинейным функциональным уравнением вида:

(2.16)

Например:


Функция f(x) должна быть априори известна.

(2.16)
Тогда выборочная оценка индекса корреляции равна [ ]:
(2.17)
Практическая формула для индекса корреляции [ ]: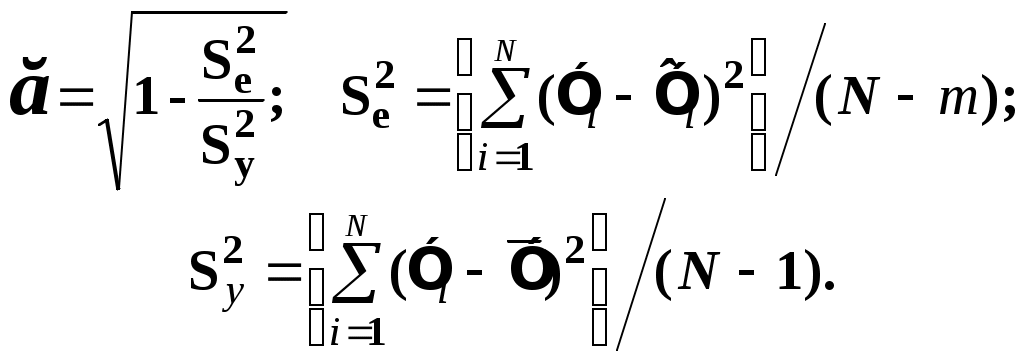
(2.18)
Здесь:

– дисперсия остатков уравнения регрессии;

– общая дисперсия как мера разброса наблюдений вокруг среднего.

Заметим, что при подстановке 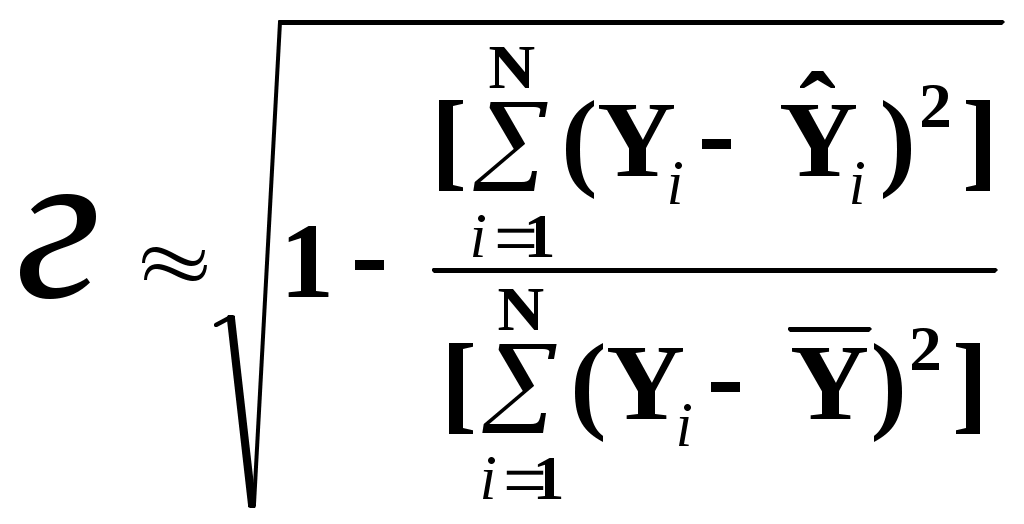и под корень в уравнении (2.18) и условии (N-m)(N-1) при больших N степени свободы и их можно сократить, откуда следует упрощенная приближенная расчетная формула.
(2.20)
Эта формула допускает наглядное толкование: чем сильнее стохастическая связь в уравнении (2.16), тем меньше доля дисперсии по отношению к общей дисперсии и больше индекса корреляции .
2.4.7. Индекс множественной корреляции
Пусть построено нелинейное уравнение множественной регрессии:
(2.20)
Тогда использую простую формулу (2.20), можно получить индекс множественной корреляции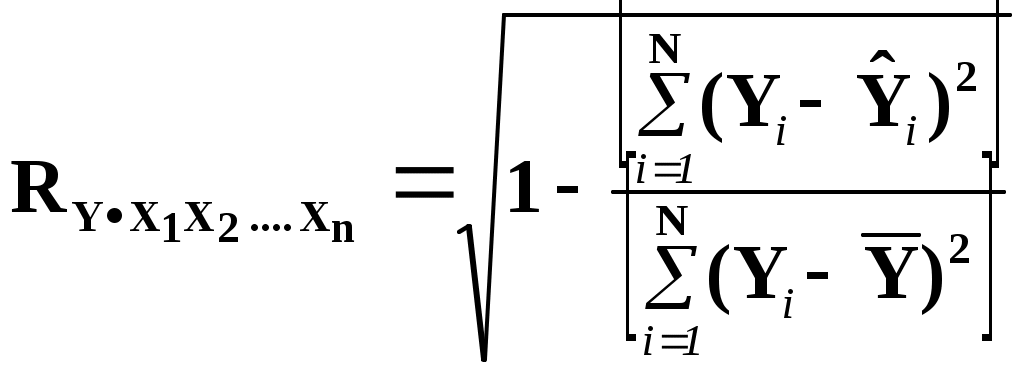
(2.21)
Соответственно квадрат этого индекса даст множественный индекс детерминации в нелинейном случае.

2.5. Коэффициент ранговой корреляции
Коэффициент ранговой корреляции служит числовой мерой стохастической связи между качественными (нечисловыми) показателями

Качественные показатели называют также ординальными и порядковыми переменными.

Пример:

На соревнованиях по фигурному катанию получена таблица оценок за «технику» T_i и «артистичность» S_i (два качественных признака).

Номер оценки	Ранги
	оценка за «технику»	оценка за «артистичность»
	признак X	признак Y
i	Ti	Si
1	T1	S1
2	T2	S2
….	….	….
N	TN	SN

Здесь T_i, S_i – ранги (баллы), т.е. значения ординальных переменных, которые находятся путем экспертных оценок (оценки судей).
Выборочная оценка, коэффициента ранговой корреляции Спирмена определяется по формуле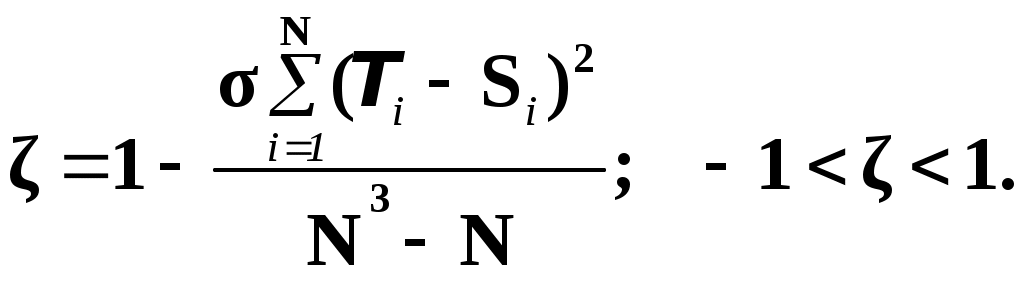
(2.22)
N – число наблюдений (строк).

Значимость коэффициента ранговой корреляции Спирмена проверяется аналогично (2.9) по критерию Стьюдента.

Глава III. Множественный регрессионный анализ
3.1. Постановка задачи
Будем постулировать выполнение основной предпосылки эконометрического анализа (1.1) – (1.5).

Пусть имеется выборка пространственного типа, т.е. кортежи наблюдений:

1). Требуется получить уравнение регрессии, для объясненной части M_x(Y) случайной величины Y, т.е. получить параметрическую оценку:

– общем случае нелинейная функция.
2). Требуется также, провести статистический анализ остатков е_i, т.е. установить: адекватна ли модель. И оценить ее погрешность.