Учебнометодический комплекс для заочного обучения с применением дистанционных технологий для студентов специальности 190702 Организация и безопасность дорожного движения
 Скачать 5.75 Mb. Скачать 5.75 Mb.
|
2.7.Виды сигналов связи и способы их обработкиАналоговые, дискретные и цифровые сигналы Одной из тенденций развития современных систем связи является широкое применение в них дискретно-аналоговой и цифровой обработки сигналов (ДАО и ЦОС). Аналоговый сигнал Z’(t), первоначально используемый в радиотехнике, может быть представлен в виде непрерывного графика (рис. 2.10а). К аналоговым сигналам относят АМ-, ЧМ-, ФМ-сигналы, сигналы телеметрического датчика и др. Устройства, в которых обрабатываются аналоговые сигналы, называются устройствами аналоговой обработки. К таким устройствам относятся преобразователи частоты, различные усилители, фильтры LC и др. Оптимальный приём аналоговых сигналов, как правило, предусматривает алгоритм оптимальной линейной фильтрации, которая актуальна особенно при использовании сложных шумоподобных сигналов. Однако именно в этом случае построение согласованного фильтра представляет большую сложность. При использовании согласованных фильтров на основе многоотводных линий задержки (магнитострикционных, кварцевых и др.) получаются большие затухания, габариты и нестабильность задержки. Перспективны фильтры на поверхностных акустических волнах (ПАВ), но малые длительности обрабатываемых в них сигналов и сложность перестройки параметров фильтров ограничивают область их применения. На смену аналоговым РЭС в 40-х годах пришли устройства дискретной обработки аналоговых входных процессов. Эти устройства обеспечивают дискретно-аналоговую обработку (ДАО) сигналов и обладают большими возможностями. Здесь применяется сигнал дискретный по времени, непрерывный по состояниям. Такой сигнал Z’(kT) представляет собой последовательность импульсов с амплитудами, равными значениям аналогового сигнала Z’(t) в дискретные моменты времени t=kT, где k=0,1,2,… - целые числа. Переход от непрерывного сигнала Z’(t) к последовательности импульсов Z’(kT) называется дискретизацией по времени. 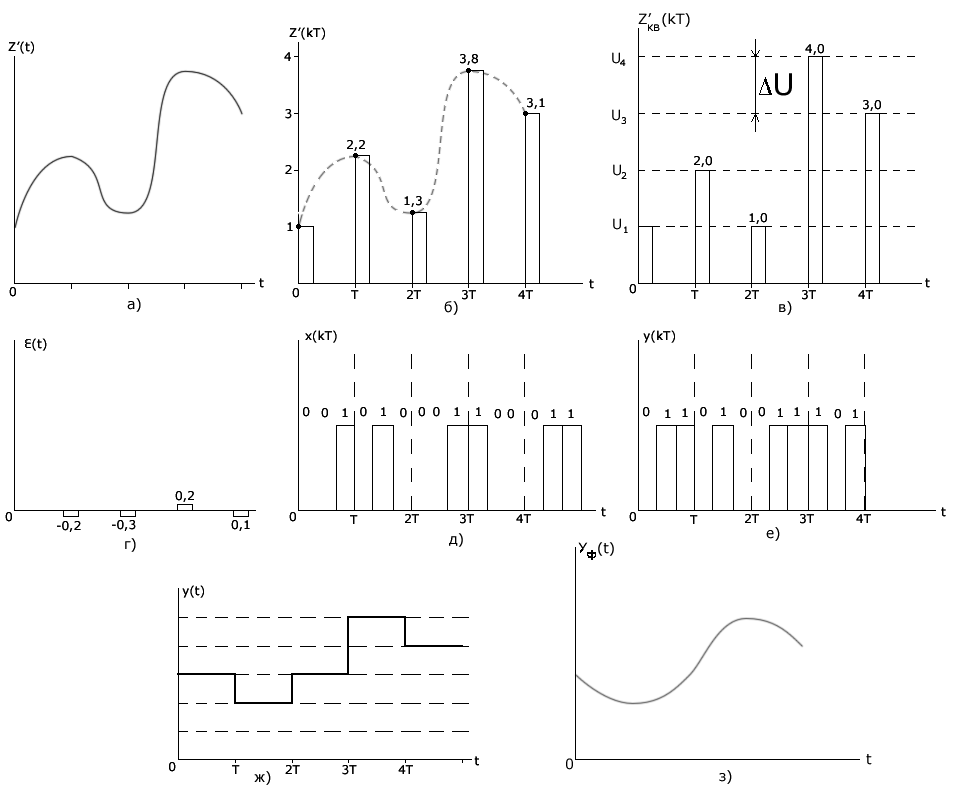 Рисунок 2.10 Аналоговые, дискретные и цифровые сигналы 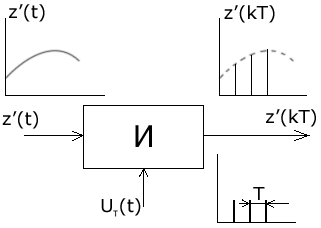 Рисунок 2.11 Дискретизация аналогового сигнала Дискретизацию аналогового сигнала по времени может выполнить каскад совпадения «И» (рис. 2.11), на входе которого действует аналоговый сигнал Z’(t). Управляется каскад совпадения тактовым напряжением UT(t) – короткими импульсами длительностью и, следующими с интервалами T>>и. Интервал дискретизации Т выбирается в соответствии с теоремой Котельникова T=1/2Fmax, где Fmax – максимальная частота в спектре аналогового сигнала. Частоту fд = 1/Т называют частотой дискретизации, а совокупность значений сигнала при 0, Т, 2Т,… - сигналом с амплитудо-импульсной модуляцией (АИМ). До конца 50-х годов сигналы АИМ применялись только при преобразовании речевых сигналов. Для передачи по каналу радиорелейной связи АИМ сигнал преобразовывают в сигнал с фазоимпульсной модуляцией (ФИМ). При этом амплитуда импульсов постоянная, а информация о речевом сообщении содержится в отклонении (фазе) импульса относительно некоторого среднего положения. Используя короткие импульсы одного сигнала, и, размещая между ними импульсы других сигналов, получают многоканальную связь (но не более 60 каналов). В настоящее время ДАО усиленно развивается на основе применения «пожарных цепочек» (ПЦ) и приборов с зарядными связями (ПЗС). В начале 70-х годов на сетях связи различных стран и СССР стали появляться системы с импульсно-кодовой модуляцией (ИКМ), где применяются сигналы в цифровой форме. Процесс ИКМ представляет собой преобразование аналогового сигнала в цифры, состоит из трёх операций: дискретизация по времени через интервалы Т (рис.2.10,б), квантование по уровню (рис. 2.10,в) и кодирования (рис. 2.10,д). Операция дискретизации по времени рассмотрена выше. Операция квантования по уровню заключается в том, что последовательность импульсов, амплитуды которых соответствуют значениям аналогового 3 сигнала в дискретные моменты времени, заменяется последовательностью импульсов амплитуды которых могут принимать только ограниченное число фиксированных значений. Эта операция приводит к ошибке квантования (рис.2.10,г). Сигнал ZКВ’(kT) является дискретным сигналом как по времени, так и по состояниям. Возможные значения u0, u1,…,uN-1 сигнала Z’(kT) на приёмной стороне известны, поэтому передают не значения uk, которое сигнал принял на интервале Т, а только его номер уровня k. На приёмной стороне по принятому номеру k восстанавливают значение uk. В этом случае передаче подлежат последовательности чисел в двоичной системе счисления – кодовые слова. Процесс кодирования заключается в преобразовании квантованного сигнала Z’(kT) в последовательность кодовых слов {x(kT)}. На рис. 2.10,д изображены кодовые слова в виде последовательности двоичных кодовых комбинаций при использовании трёх разрядов. Рассмотренные операции ИКМ применяются в РПУ с ЦОС, при этом ИКМ необходима не только для аналоговых сигналов, но и для цифровых. Покажем необходимость ИКМ при приёме цифровых сигналов по радиоканалу. Так, при передаче в декаметровом диапазоне элемент xxxxxxxxxxxxxxxxxxxxxxа цифрового сигнала xi(kT) (i=0,1), отражающего n-ой элемент кода, ожидаемый сигнал на входе РПУ вместе с аддитивной помехой ξ(t) можно представить в виде: z/i(t)= µx(kT) + ξ(t) , (2.2) при (0 ≤ t ≥ TЭ), где μ- коэффициент передачи канала, ТЭ – время длительности элемента сигнала. Из (2.2) видно, что помехи на входе РПУ образуют множество сигналов, представляющих собой аналоговое колебание. Примерами цифровых схем являются логические элементы, регистры, триггеры, счетчики, запоминающие устройства и др. По количеству узлов на ИС и БИС, РПУ с ЦОС делят на две группы: 1. Аналого-цифровые РПУ, которые имеют реализованные на ИС отдельные узлы: синтезатор частоты, фильтры, демодулятор, АРУ и др. .2. Цифровые радиоприёмные устройства (ЦРПУ), в которых сигнал обрабатывается после аналого-цифрового преобразователя (АЦП). На рис. 2.12 показаны элементы основного (информационного канала) ЦРПУ декаметрового диапазона:: аналоговая часть приёмного тракта (АЧПТ), АЦП (состоящий из дискретизатора, квантователя и кодера), цифровая часть приёмного тракта (ЦЧПТ), цифро-аналоговый преобразователь (ЦАП) и фильтр нижних частот (ФНЧ). Двойные линии обозначают передачу цифровых сигналов (кодов), а одинарные – аналоговых и АИМ сигналов. 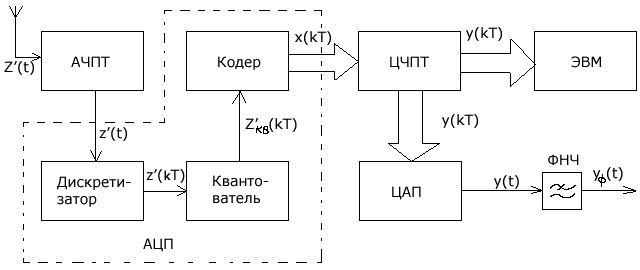 Рисунок 2.12 Элементы основного (информационного канала) ЦРПУ декаметрового диапазона АЧПТ производит предварительную частотную избирательность, значительное усиление и преобразование сигнала Z’(T) по частоте. АЦП преобразует аналоговый сигнал Z’(T) в цифровой x(kT) (рис. 2.10,д). В ЦЧПТ как правило производится дополнительное преобразование по частоте, избирательность (в цифровом фильтре – основной избирательности) и цифровая демодуляция аналоговых и дискретных сообщений (частотной, относительной фазовой и амплитудной телеграфии). На выходе ЦЧПТ получаем цифровой сигнал y(kT) (рис. 2.10,е). Этот сигнал, обработанный по заданному алгоритму, с выхода ЦЧПТ поступает в ЦАП или в запоминающее устройство ЭВМ (при приёме данных). В последовательно включённых ЦАП и ФНЧ, цифровой сигнал y(kT) преобразуется вначале в непрерывный по времени и дискретный по состояниям сигнал y(t), а затем в yФ(t), который непрерывный по времени и по состояниям (рис. 2.10,ж, з). Из многих методов цифровой обработки сигналов в ЦРПУ важнейшими являются цифровая фильтрация и демодуляция. Рассмотрим алгоритмы и структуру цифрового фильтра (ЦФ) и цифрового демодулятора (ЦД). Цифровой фильтр – это дискретная система (физическое устройство или программа для ЭВМ). В нём последовательность числовых отсчётов {x(kT)}входного сигнала преобразуется в последовательность {y(kT)}выходного сигнала. Основными алгоритмами ЦФ являются: линейное разностное уравнение, уравнение дискретной свёртки, операторная передаточная функция в z-плоскости и частотная характеристика. Уравнения, которые описывают последовательности чисел (импульсов) на входе и выходе ЦФ (дискретной системы с задержкой), называются линейными разностными уравнениями. Линейное разностное уравнение рекурсивного ЦФ имеет вид: 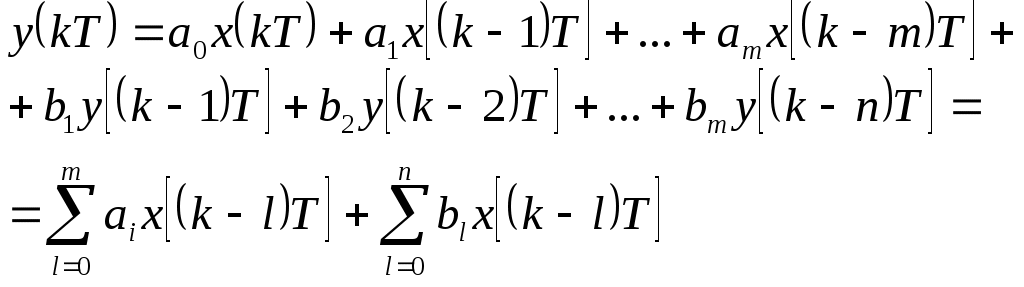 , (2.3) , (2.3)где x[(k-m)T] и y[(k-n)T] – значения входных и выходных последовательностей числовых отсчётов в моменты времени (k-m)T и (k-n)Т соответственно; m и n – число задержанных суммируемых предыдущих входных и выходных числовых отсчётов соответственно; a0, a1, …, am и b1, b2, …, bn – вещественные весовые коэффициенты. В (3) первое слагаемое является линейным разностным уравнением нерекурсивного ЦФ. Уравнение дискретной свёртки ЦФ получают из линейного разностного нерекурсивного ЦФ путём замены в нём al на h(lT): где h(lT) – импульсная характеристика ЦФ, представляющая собой отклик на единичный импульс. Операторная передаточная функция есть отношение преобразованных по Лапласу функций на выходе и входе ЦФ: Эту функцию получают непосредственно из разностных уравнений, применяя дискретное преобразование Лапласа и теорему смещения. Под дискретным преобразованием Лапласа, например, последовательности {x(kT)} понимается получение L – изображения вида где p=+j - комплексный оператор Лапласа. Теорему смещения (сдвига) применительно к дискретным функциям можно сформулировать: смещение независимой переменной оригинала во времени на mT соответствует умножению L –изображения на Учитывая свойства линейности дискретного преобразования Лапласа и теорему смещения, выходная последовательность чисел нерекурсивного ЦФ примет вид Тогда операторная передаточная функция нерекурсивного ЦФ: 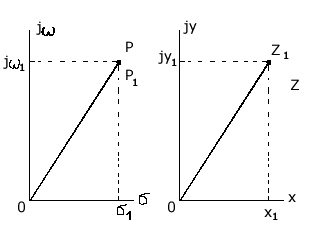 Рисунок 2.13 Аналогично, учитывая формулу (2.3), получим операторную передаточную функцию рекурсивного ЦФ: 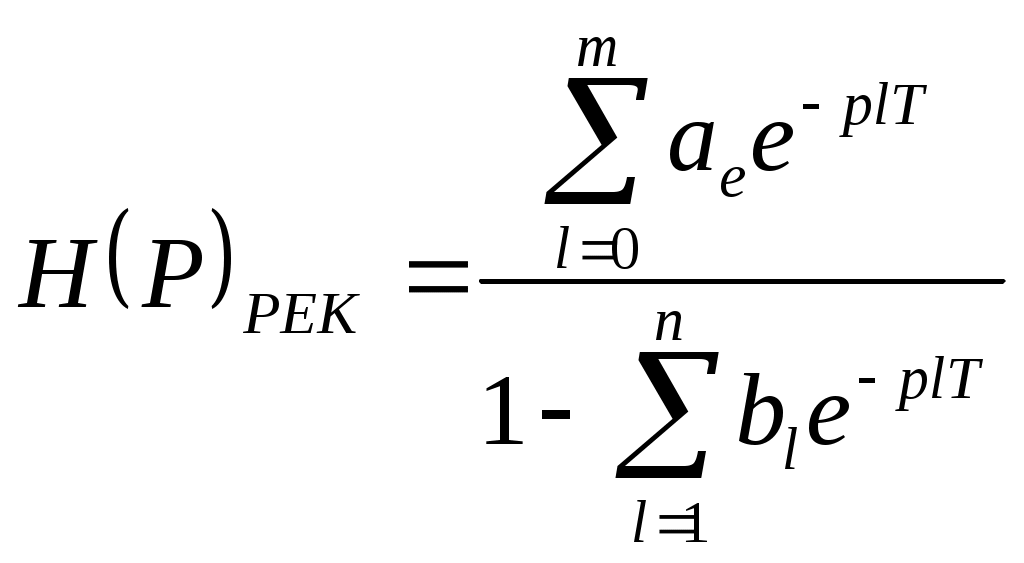 , (2.10) , (2.10) . Формулы операторных передаточных функций имеют сложный вид. Поэтому большие трудности возникают при исследовании полей и полюсов (корней рис. 2.13 полинома числителя и корней полинома знаменателя), которые в р-плоскости имеют периодическую по частоте структуру. Анализ и синтез ЦФ упрощается при применении z – преобразования, когда переходят к новой комплексной переменной z, связанной с p соотношением z=epT или z-1=e-рT. Здесь комплексная плоскость р=+j отображается другой комплексной плоскостью z=x+jy. Для этого необходимо, чтобы e+j=x+jy. На рис. 2.13 показаны комплексные плоскости р и z. Сделав замену переменных e-pT=z-1 в (2.9) и (2.10), получим передаточные функции в z-плоскости соответственно для нерекурсивного и рекурсивного ЦФ: 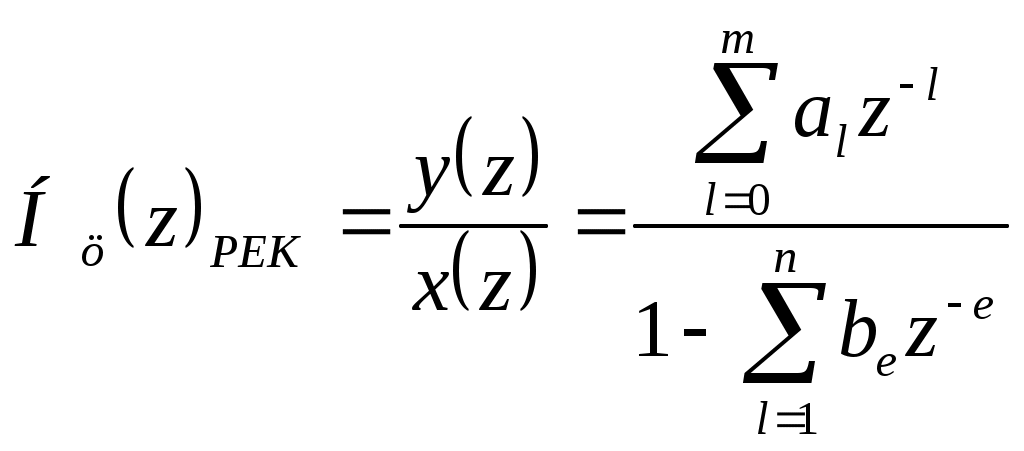 , (2.12) , (2.12)Передаточная функция нерекурсивного ЦФ имеет только нули, поэтому он абсолютно устойчив. Рекурсивный ЦФ будет устойчивым, если его полюсы будут расположены внутри единичного круга z-плоскости. Передаточная функция ЦФ в виде полинома по отрицательным степеням переменной z дает возможность непосредственно по виду функции HЦ(z) составить структурную схему ЦФ. Переменную z-1 называют оператором единичной задержки, а на структурных схемах это элемент задержки. Поэтому старшие степени числителя и знаменателя передаточной функции HЦ(z)рек определяют количество элементов задержки соответственно в нерекурсивной и рекурсивной частях ЦФ. Частотную характеристику ЦФ получают непосредственно из его передаточной функции в z-плоскости путём замены z на ej (или z-1 на e-j) и проведения необходимых преобразований. Поэтому частотную характеристику можно записать в виде: где КЦ() – амплитудно-частотная (АЧХ), а φ() – фазочастотная характеристики ЦФ; =2 Характеристика КЦ(j) ЦФ является периодической функцией цифровой частоты с периодом 2 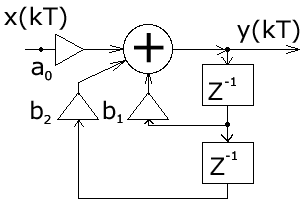 Рисунок 2.14 Структурная схема колебательного контура В радиотехнике при аналоговой обработке сигнала простейшим частотным фильтром является колебательный контур LC. Покажем, что при цифровой обработке простейшим частотным фильтром является рекурсивное звено второго порядка, передаточная функция в z-плоскости которого а структурная схема имеет вид, изображенный на рис. 2.14. Здесь оператор Z-1 является дискретным элементом задержки на один такт работы ЦФ, линии со стрелками обозначают умножение на a0, b2, и b1, «блок +» обозначает сумматор. Для упрощения анализа в выражении (2.14) примем a0=1, представив его по положительным степеням z, получим . Передаточная функция цифрового резонатора также как и колебательный LC-контур зависит только от параметров цепи. Роль L,C,R выполняют коэффициенты b1 и b2. Из (2.15) видно, что передаточная функция рекурсивного звена второго порядка имеет в плоскости z ноль второй кратности (в точки z=0) и два полюса 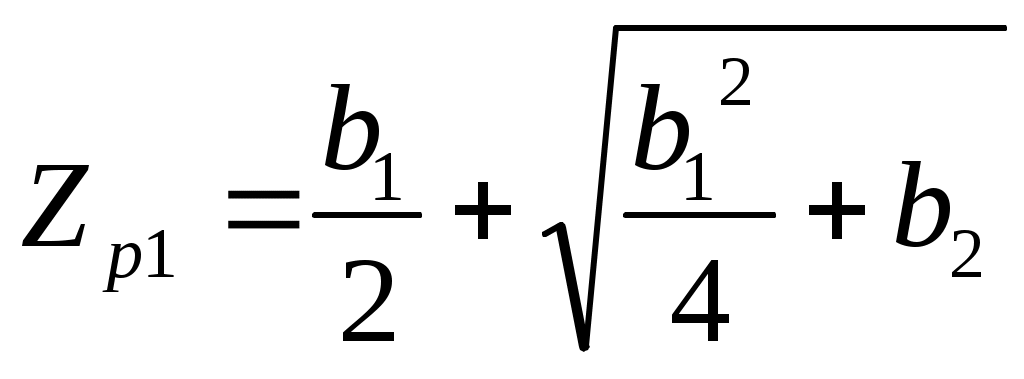 и и 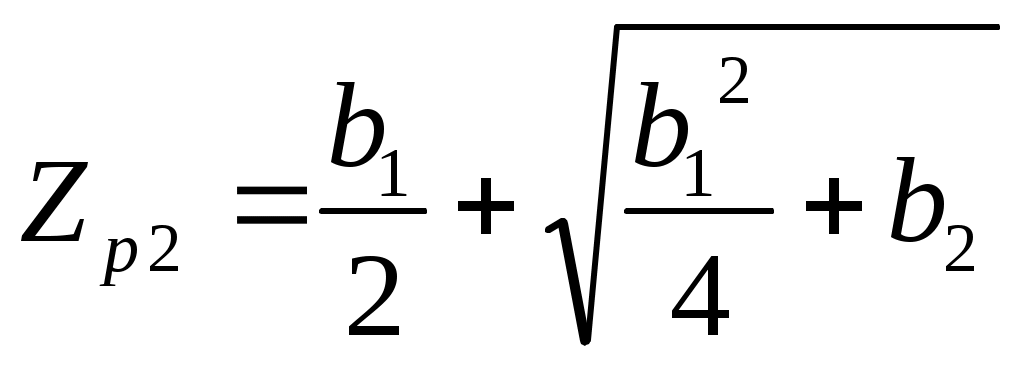 Уравнение частотной характеристики рекурсивного звена второго порядка получим из (2.14), заменяя z-1 на e-j (при a0=1): 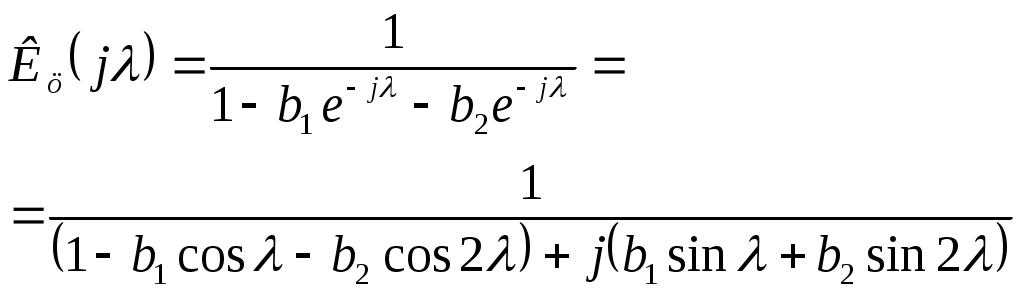 , (2.16) , (2.16)Амплитудно-частотная характеристика равна модулю (2.16): После проведения элементарных преобразований. АЧХ рекурсивного звена второго порядка примет вид: 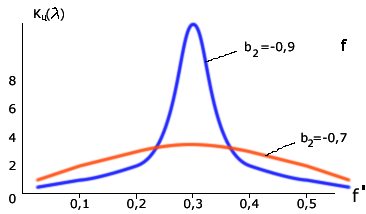 Рисунок 2.15 График рекурсивного звена второго порядка На рис. 2.15 изображены графики в соответствии с (2.18) при b1=0. Из графиков видно, что рекурсивное звено второго порядка является узкополосной избирательной системой, т.е. цифровым резонатором. Здесь показан только рабочий участок частотного диапазона резонатора f ’<0,5. Далее характери-стики повторяются с интервалом fД Исследования показывают, что резонансная частота f0’ будет принимать следующие значения: f0’=fД/4 при b1=0; f0’ f0’>fД/4 при b1<0. Значения b1 и b2 изменяют как резонансную частоту, так и добротность резонатора. Если b1 выбирать из условия Цифровой демодулятор Цифровой демодулятор в общей теории связи рассматривается как вычислительное устройство, которое выполняет обработку смеси сигнала и помех. Определим алгоритмы ЦД при обработке аналоговых сигналов АМ и ЧМ с высоким отношением сигнал/шум. Для этого представим комплексную огибающую Z/(t) узкополосной аналоговой смеси сигнала и помех Z’(t) на выходе АЧПТ в показательной и алгебраической форме: Здесь 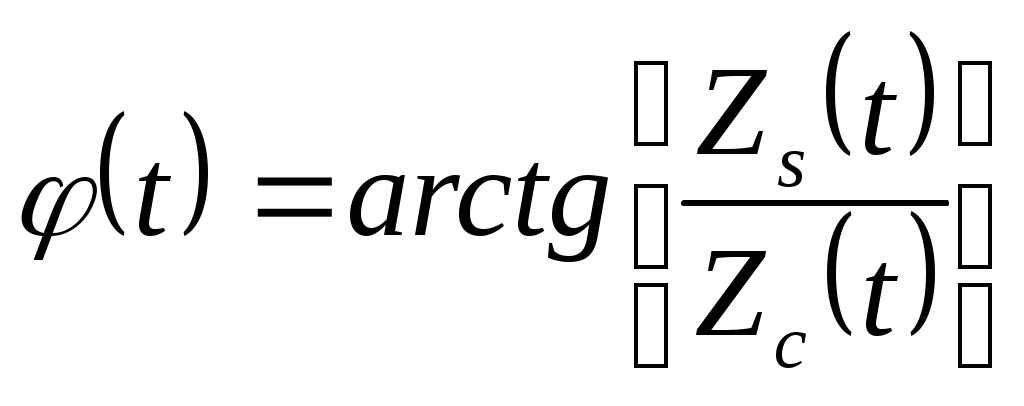 , (2.20) , (2.20)является огибающей и полной фазой смеси, а ZC(t) и ZS(t) – квадратурные составляющие. Из (2.20) видно, что огибающая сигнала Z(t) содержит полную информацию о законе модуляции. Поэтому цифровой алгоритм обработки аналогового АМ-сигнала в ЦД с использованием квадратурных составляющих XC(kT) и XS(kT) цифрового сигнала x(kT) имеет вид: Известно, что частота сигнала является первой производной от его фазы, т.е. Тогда из (2.20) и (2.22) следует: 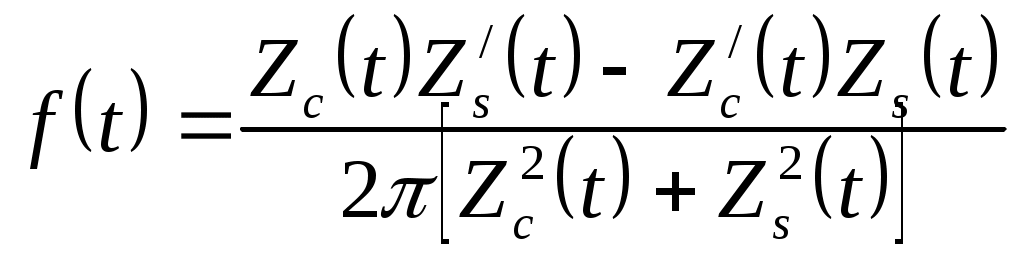 , (2.23) , (2.23)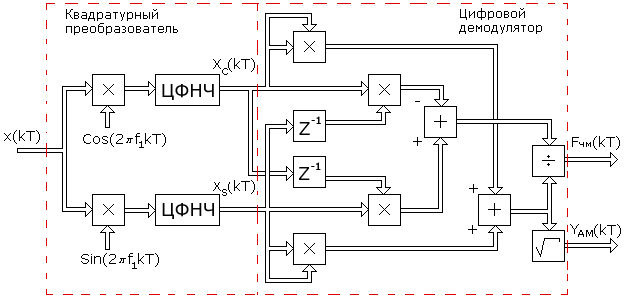 Рисунок 2.16 Структурная схема ЦЧПТ Используя в (2.23) квадратурные составляющие XC(kT) b XS(kT) цифрового сигнала x(kT) и заменяя производные первыми разностями, получим цифровой алгоритм обработки аналогового ЧМ-сигнала в ЦД: 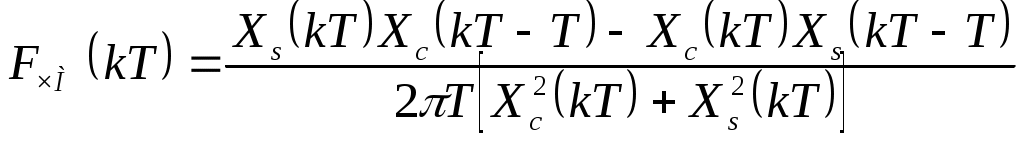 , (2.24) , (2.24)На рис. 2.16 показан вариант структурной схемы ЦЧПТ при приеме аналоговых сигналов АМ и ЧМ, которая состоит из квадратурного преобразователя (КП) и ЦД. В КП образуются квадратурные составляющие комплексного цифрового сигнала путем перемножения сигнала x(kT) на две последовательности {cos(2πf1kT)} и {sin(2πf1kT)}, где f1 – центральная частота самого низкочастотного отображения спектра сигнала z’(t). На выходе перемножителей цифровые фильтры нижних частот (ЦФНЧ) обеспечивают подавление гармоник с частотой 2f1 и выделяют цифровые отсчеты квадратурных составляющих. Здесь ЦФНЧ используются в качестве цифрового фильтра основной избирательности. Структурная схема ЦД соответствует алгоритмам (2.21) и (2.24). Рассмотренные алгоритмы цифровой обработки сигналов можно реализовать аппаратным методом (с помощью специализированных вычислителей на цифровых ИС, приборов с зарядной связью или приборов на поверхностно-акустических волнах) и в виде программ на ЭВМ. При программной реализации алгоритма обработки сигналов ЭВМ выполняет арифметические операции над хранящимися в ней коэффициентами al, bl и переменными x(kT), y(kT). Ранее недостатками вычислительных методов были: ограниченное быстродействие, наличие специфических погрешностей, необходимость переселекции, большая сложность и стоимость. В настоящее время эти ограничения успешно преодолеваются. Преимуществами устройств цифровой обработки сигналов перед аналоговыми являются совершенные алгоритмы связанные с обучением и адаптацией сигналов, простота управления характеристиками, высокая временная и температурная стабильность параметров, высокая точность и возможность одновременной и независимой обработки нескольких сигналов. Простые и сложные сигналы. База сигнала Характеристики (параметры) систем связи улучшались по мере освоения видов сигналов и их способов приема, обработки (разделения). Каждый раз возникала необходимость в грамотном распределении ограниченного частотного ресурса между работающими радиостанциями. Параллельно этому решался вопрос уменьшения полосы излучения сигналами. Однако были проблемы при приеме сигналов, которые простым распределением частотного ресурса не решались. Только применение статистического способа обработки сигналов – корреляционного анализа позволило решить эти проблемы. Простые сигналы имеют базу сигнала BS=TS*∆FS≈1, (2.25) где TS – длительность сигнала; ∆FS – ширина спектра простого сигнала. Системы связи, работающие на простых сигналах, называют узкополосными. У сложных (составных, шумоподобных) сигналов за время длительности сигнала TS происходит дополнительная модуляция (манипуляция) по частоте или по фазе. Поэтому здесь применяется следующее соотношение для базы сложного сигнала: BSS=TS*∆FSS>>1, (2.26) где ∆FSS – ширина спектра сложного сигнала. Иногда говорят, что у простых сигналов ∆FS = 1/ TS является спектром сообщения. У сложных сигналов спектр сигналов расширяется в ∆FSS / ∆FS раз. При этом получается избыточность в спектре сигнала, которая определяет полезные свойства сложных сигналов. Если в системе связи со сложными сигналами увеличить скорость передачи информации, чтобы получить длительность сложного сигнала TS = 1/ ∆FSS , то образуется опять простой сигнал и узкополосная система связи. Полезные свойства системы связи исчезают. Способы расширения спектра сигнала Рассмотренные выше дискретные и цифровые сигналы – это сигналы временным разделением. Ознакомимся с широкополосными цифровыми сигналами и с методами многостанционного доступа с кодовым (по форме) разделением каналов. Вначале широкополосные сигналы применялись в военной и в спутниковой связи.из-за их полезных свойств. Здесь использовались их высокая защищенность от помех и скрытность Система связи с широкополосными сигналами может работать, когда невозможен энергетический перехват сигнала, а подслушивание без наличия образца сигнала и без специальной аппаратуры невозможно и при принятом сигнале. Использовать отрезки белого теплового шума в качестве переносчика информации и метод широкополосной передачи предложил Шеннон. Он ввел понятие пропускной способности канала связи. Показал связь между возможностью безошибочной передачей информации с заданным отношением Первой системой связи со сложными сигналами из отрезков белого теплового шума была предложена Костасом. В Советском Союзе применять широкополосные сигналы, когда реализуется метод многостанционного доступа с кодовым разделением каналов, предложил Л. Е. Варакин. Для временного представления любого варианта сложного сигнала можно записать соотношение: где UI (t) и Функциями по сравнению с cosω0t; При частотном представлении сигнала его обобщенная спектральная форма имеет вид 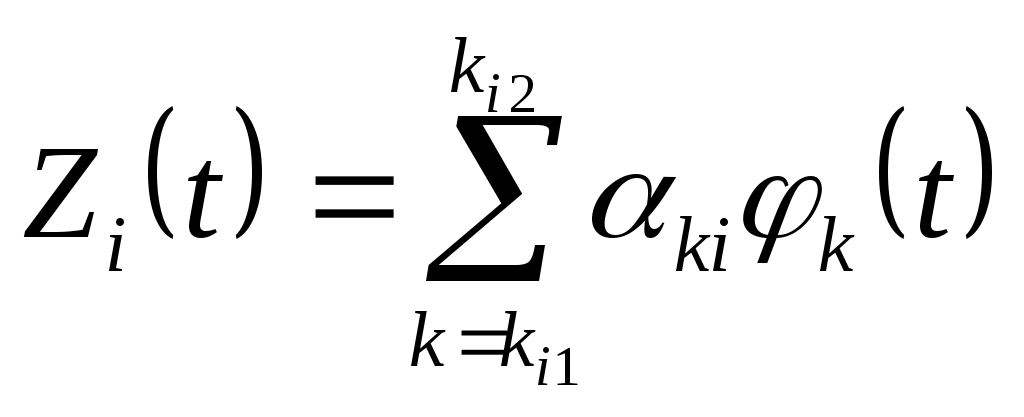 , , где Координатные функции должны удовлетворять условию ортогональности 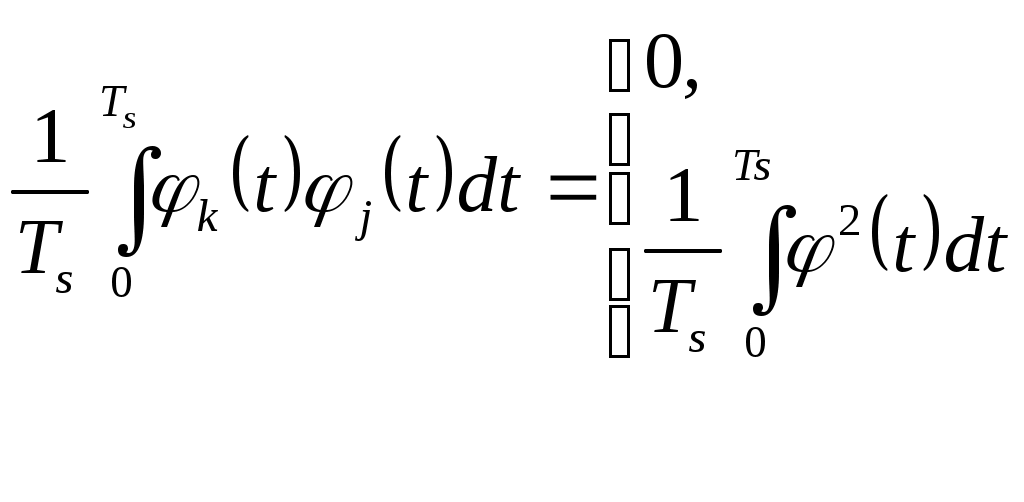 , (2.29) , (2.29) а коэффициенты разложения 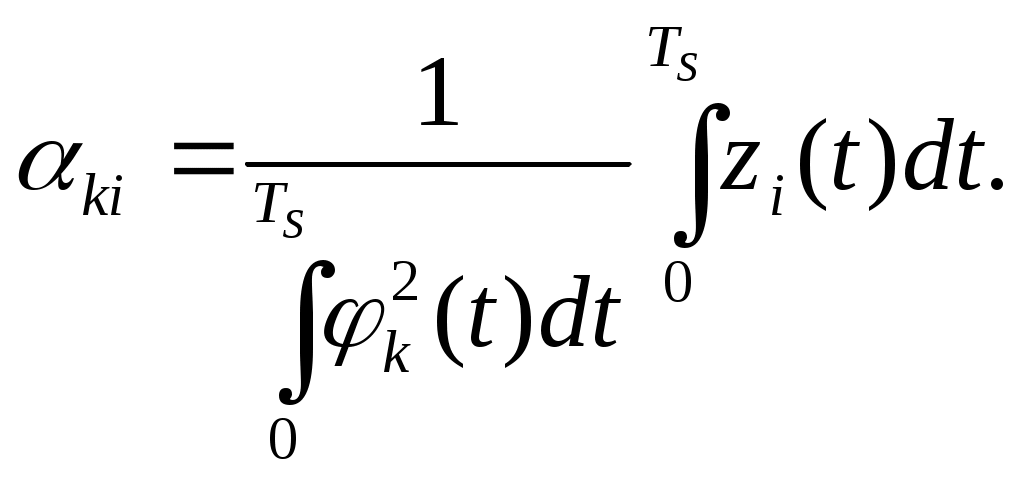 (2.30) (2.30)Для параллельных сложных сигналов в качестве координатных функций вначале использовали тригонометрические функции кратных частот  , (2.31) , (2.31)когда каждый i-й вариант сложного сигнала имеет вид 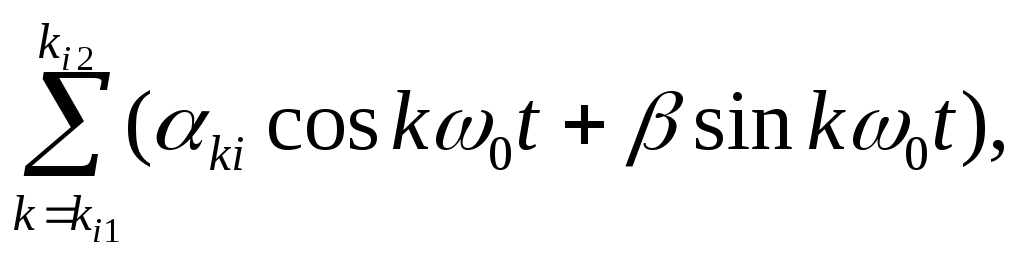 t t Тогда, приняв Aki = i = 1,2,3,,…,m ; m – основание кода, получаем Z i (t) = 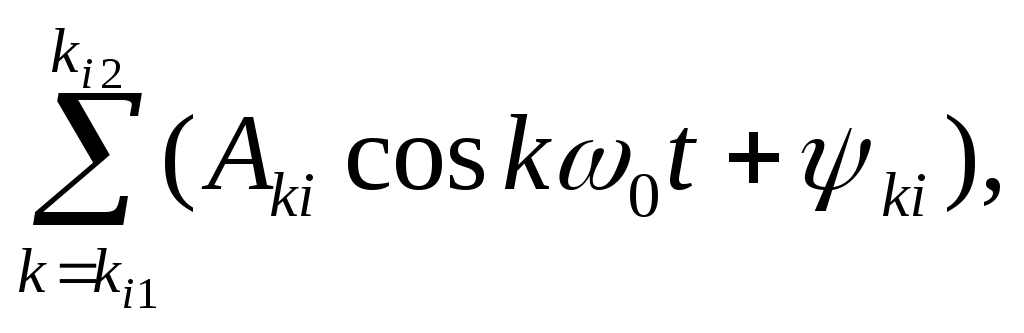 t t Здесь составляющие сигнала занимают частоты от ki1 Полоса частот, занимаемая сигналом ∆FSS = (ki2 - ki1 + 1)ω0 / 2π = (ki2 - ki1 + 1)/ TS . (2.35) В ней сосредоточена основная часть энергетического спектра сигнала. Из соотношения (35) следует, что база этого сигнала BSS = TS ∙ ∆FSS = (ki2 - ki1 + 1) = Ni , (2.36) равна числу гармонических составляющих сигнала Ni, которые формирует i-й вариант сигнала 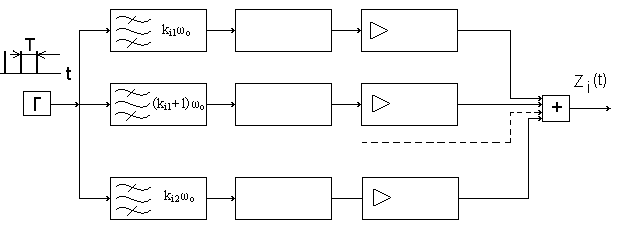 а) 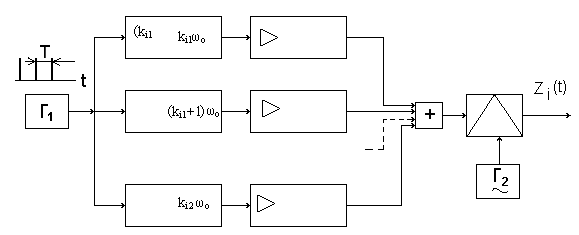 б) Рисунок 2.17  а) б) 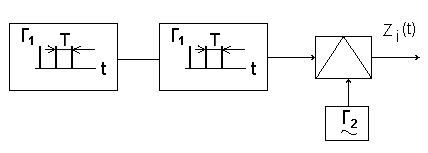 Рисунок 2.18 Схема расширения спектра сигнала с графиком периодической последовательности С 1996-1997 годов в коммерческих целях компания Qualcomm начала применять для формирования параллельных сложных сигналов на основе (28) подмножества {φk(t)} полных ортогонализированных на интервале [0, TЭ] функций Уолша. При этом реализуется метод многостанционного доступа с кодовым разделением каналов – стандарт CDMA (Code Division Multiple Access)  Рисунок 2.19 Схема корреляционного приемника Полезные свойства широкополосных (составных) сигналов  Рисунок 2.20 При связи с подвижными станциями (ПС) проявляется многолучевое (многопутевое) распространение сигнала. Поэтому возможна интерференция сигнала, которая приводит к появлению в пространственном распределению электромагнитного поля глубоких провалов (замираний сигналов). Так в городских условиях в точке приема может быть только переотраженные сигналы от высотных зданий, холмов и т.д., если отсутствует прямая видимость. Поэтому два сигнала с частотой 937,5 МГц ( = 32см), пришедшие со сдвигом во времени на 0,5 нс при разнице в пути 16см, складываются в противофазе. Уровень сигнала на входе приемника изменяется и от проходящего мимо станции транспорта. Узкополосные системы связи не могут работать в условиях многолучевости. Так если на входе такой системы будет три луча сигнала одной посылки Si(t) –Si1(t), Si2(t), Si3(t), которые перекрываются во времени за счет разницы в длине пути прохождения, то их разделить на выходе полосового фильтра (Yi1(t), Yi2(t), Yi3(t)) невозможно. Системы связи со сложными сигналами противостоят многолучевому характеру распространения радиоволн. Так, выбирая полосу ∆FSS такой, чтобы длительность свернутого импульса на выходе корреляционного детектора или согласованного фильтра была меньше времени запаздывания соседних лучей, можно принять один луч или, обеспечив соответствующие задержки импульсов (Gi(t)), сложить их энергию, что увеличит соотношение сигал/шум. Американская система связи Rake подобно граблям собирала принимаемые лучи, отраженного от Луны сигнала и суммировали их. Принцип накопления сигнала позволяет значительно улучшить помехоустойчивость и другие свойства сигнала. Представление о накоплении сигнала дает простое повторение сигнала. Первым элементом для этой цели использовалась частотно-избирательная система (фильтр). Корреляционный анализ позволяет определить статистическую связь (зависимость) между принятым сигналом и эталонным сигналом, находящимся на приемной стороне. Понятие о корреляционной функции ввел Тейлор в 1920г. Корреляционная функция – это статистическое среднее значение второго порядка по времени, или спектральное среднее значение, или вероятностное среднее значение. Если временные функции (непрерывные последовательности) x(t) и y(t) имеют средние арифметические значения то взаимная корреляционная функция выражается интегралом (средним значением) и зависит от параметра задержки τ – времени накопления значения функции. При x(t) = y(t) образуется функция автокорреляции, а при x(t) Разделение сигналов при представленииих рядами и интегралами Фурье На базе основных соотношений и определений покажем множественный доступ (разделение сигналов): - с частотным разделением каналов; - с временным разделением каналов; - с кодовым разделением каналов. Периодическая функция имеет вид: f(t) = f(t+kT), (2.40) где T-период, k-любое целое число (k= На рис.2.10,а,б,в изображен периодический гармонический сигнал u1(t) и его спектр амплитуд и фаз. На рис.2.11,а,б,в изображены графики периодического сигнала u2(t) - последовательности прямоугольных импульсов и его спектр амплитуд и фаз. Итак, любые сигналы можно на определенном промежутке времени представить в виде ряда Фурье. Тогда разделение сигналов будем представлять через параметры сигналов, т. е. через амплитуды, частоты, и фазовые сдвиги: а) сигналы, ряды которых с произвольными амплитудами, не перекрывающими частотами и произвольными фазами разделяются по частоте; б) сигналы, ряды которых с произвольными амплитудами, перекрываются по частоте, но сдвинутыми по фазе между соответствующими составляющими рядов разделяются по фазе (фазовый сдвиг здесь пропорционален частоте); Высокая емкость систем связи с составными сигналами будет показана ниже. в) сигналы, ряды которых с произвольными амплитудами, с составляющими перекрывающимися по частоте (частоты могут совпадать) и произвольными фазами разделяются по форме. Разделение по форме – это кодовое разделение, когда на передающей и приемной сторонах имеются специально созданные из простых сигналов сложные сигналы (образцы). При приеме сложный сигнал вначале подвержен корреляционной обработке, а затем идет обработка простого сигнала. Разделение частотного ресурса при множественном доступе В настоящее время сигналы могут передаваться в любых средах (в окружающем пространстве, в проводе, в волоконно-оптическом кабеле и др.). Для повышения эффективности частотного спектра, а за одно и линии передачи образуют групповые каналы для передачи сигналов по одной линии связи. На приемной стороне происходит обратный процесс – разделение каналов. Рассмотрим используемые способы разделения каналов:  Рисунок 2.21 Частотное разделение каналов (Frequency Division Multiple Access FDMA)  Рисунок 2.22 Временное разделение каналов (Time Division Multiple Access TDMA). 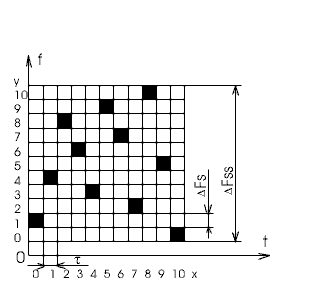 а) 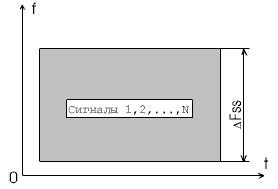 б) Рисунок 2.23 Кодовое разделение каналов (Code Division Multiple Access CDMA) |
