ФИЗИКА Пraktikum. Учебнометодическое пособие для студентов медицинских вузов 2018 Вводное занятие
 Скачать 4.99 Mb. Скачать 4.99 Mb.
|
|
Та из двух сред, у которой абсолютный показатель больше, называется оптически более плотной средой. Показатель преломления воздуха, как видно из таблицы 1, весьма близок к единице, и во многих случаях его можно принять за единицу. Вместе с тем, из «воздушной» строки этой таблицы заметно, что измерение значений абсолютного показателя преломления можно производить с высокой точностью, до миллионных долей единицы. Подобные измерения применяются, в частности, при контроле экологической обстановки. Земная атмосфера существенно неоднородна. Из множества показателей, характеризующих состояние атмосферы, мы в повседневной жизни особо выделяем температуру воздуха и атмосферное давление. Их изменчивость общеизвестна. Но от них зависит не только наше самочувствие, но также значения менее ощутимых для нас параметров: плотность воздуха и соответствующее ей значение показателя преломления. Они, вслед за температурой и давлением, неоднородны и в пространстве, и во времени. На границе раздела слоев воздуха с несколько различными показателями преломления происходит плавное, как бы смазанное, преломление лучей от слоя к слою, чуть заметное искривление светового луча. В итоге, в неоднородной земной атмосфере световые лучи не вполне прямолинейны. Оптические методы наблюдений и измерений основаны на постулате прямолинейности световых лучей. Если же они криволинейны, то связанные с этим погрешности измерений тем больше, чем больше необходимая длина пробега световых лучей. Кстати, какие это погрешности: системамические или случайные? Для некоторых задач астрономии и геодезии такие погрешности имеют принципиальное значение: - астрономическая рефракция – преломление света на неоднородностях атмосферы в вертикальном и наклонных направлениях. Искривленные лучи порождают погрешности в определении координат небесных объектов. - геодезическая рефракция – преломление света на неоднородностях атмосферы в горизонтальных направлениях. Искривленные световые лучи порождают погрешности координат объектов на геодезических картах. 3. Дисперсия света. Дисперсией света называется свойство света сложного состава распадаться при преломлении на простые компоненты, зрительно воспринимаемые как разноцветные лучи близких направлений.Дисперсия объясняется тем, что показатель преломления вещества является некоторой функцией от длины световой волны. Компоненты света с различной длиной волны различной преломляются по-разному.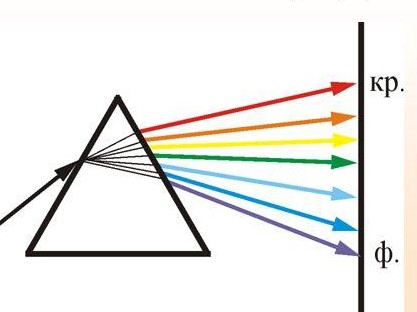 На рис. 3 - схема опытов Ньютона по изучению дисперсии света. Слева от стеклянной призмы – падающий солнечный луч. Справа, на вертикальном экране – непрерывный спектр солнечного света (его видимая часть). Цвета – от красного (кр.) до фиолетового (ф.) Рис. 3. Дисперсия солнечного света (схема опыта Ньютона). Примечания к рис. 3: При прохождении призмы свет преломился дважды. Разложение солнечного луча в спектр произошло при первом преломлении. Второе преломление привело лишь к некоторому увеличению угловой расходимости лучей на выходе из призмы. На схеме рис. 3 не показаны лучи, отраженные от правой грани призмы. Можно бы наблюдать спектр и на горизонтальном экране, расположенном под призмой. Вопросик: какова, читая слева направо, должна быть последовательность цветов на горизонтальном экране? Радуга – пример природного явления, объяснение которому – в совместно происходящих преломлении, дисперсии и отражении света. Первую теорию радуги предложил Рене Декарт (1637 год). Радуга возникает, когда солнце – где-то позади вас, и его косые лучи подсвечивают дождевые тучи. В мельчайших, а потому медленно оседающих дождевых каплях происходит следующее: - преломление солнечного света на входе в капли, на ближних к вам поверхностях капель, сопровождающееся дисперсией света, – внутри капель - отражение разложенного в спектр света от дальних поверхностей капель, – второе преломление: на ближних к вам поверхностях капель, с выходом разноцветных лучей в сторону Ваших восхищенных глаз. 4. Полное внутреннее отражение света. Эндоскопия. Явление полного внутреннего отражения может наблюдаться, если световой луч идет из оптически более плотной среды в оптически менее плотную. При переходе света из среды, оптически более плотной, в менее плотную, угол преломления оказывается больше, чем угол падения: γ 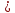 α, (см. рис. 4А) α, (см. рис. 4А)Убедимся в этом расчетным путем на примере перехода луча из стекла (n1=1,5) воздух (n2=1). Согласно формуле (1), относительный показатель преломления воздуха относительно стекла nв-ст=1/1,5. Отсюда следует: 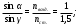 Отсюда получаем, что sin γ = 1,5‧sinα; следовательно, γ 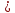 α. α. Если увеличивать угол паления α, то угол преломления γ будет увеличиваться быстрее, чем α, и при некотором (предельном) значении угла падения αпр угол преломления достигнет значения γ=90° (схема В на рис. 4): преломленный луч скользит по границе раздела двух сред. При углах падения α>αпр явление преломления не происходит, а вместо частичного отражения на границе раздела двух сред происходит полное отражение света внутрь оптически более плотной среды - полное внутреннее отражение. Это оптическое явление составляет основу целого физико-технического направления: волоконная оптика. 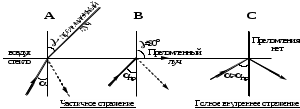 Рис. 4. Стадии перехода от частичного к полному внутреннему отражению. Вам, вероятно, встречались декоративные светильники, представляющие собой букет из свободно изогнувшихся тонких прозрачных волокон. В непрозрачном корпусе светильника находится плотный жгут из этих волокон, их торцы освещены обычной электрической лампочкой. Свет, проникающий в волокно с торца, испытывая многократное полное внутреннее отражение, распространяется вдоль этого волокна, каким бы изогнутым оно ни оказалось, и выходит из него, только достигнув его противоположного торца. А поскольку диаметр волокна гораздо больше, чем длина световой волны, то свет выходит из конца волокна в большом телесном угле, и светящийся конец волокна похож на яркую звездочку, видимую со всех сторон. В медицине волоконная оптика нашла применение в эндоскопах - устройствах для осмотра внутренних полостей. Световод, представляющий собой жгут из большого числа тонких стеклянных волокон, помещенных в общую защитную оболочку, вводится в исследуемую полость. Часть волокон может использоваться для передачи во внутреннюю полость лазерного излучения в лечебных целях. Эндоскопы становятся все более совершенными. Современные эндоскопы позволяют не только визуально обследовать внутренние полости тела, но и выполнять прицельную биопсию (забор пробы тканей), удалять инородные предметы (пуговицы, и т.п.), удалять полипы, прижигать кровоточащие сосуды. На рис. 5 показана схема фиброгастроскопического обследования желудка. Здесь fibro (лат.) – волокно, так что в длинном термине - намек на гибкость волоконнооптического эндоскопа. Существуют и жесткие эндогастроскопы. Однако у волоконной оптики в области эндоскопии обозначился сильный конкурент: на смену толстым фиброгастроскопам идут тонкие видеоэндоскопы, имеющие на конце миниатюрную видеокамеру. Такая техника дает изображение гораздо более высокого качества. 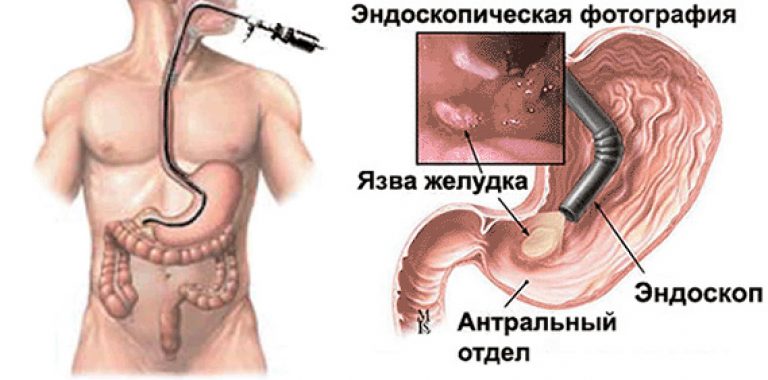 Рис. 5. Схема эндоскопического обследования желудка. 5. Линзы. Характеристики линз. В Британском музее хранится линза, возраст которой – более 3000 лет. Эта плоско-выпуклая грубовато отшлифованная линза дает (до сих пор) 3-х кратное увеличение. Наши далекие предки использовали подобные линзы для добывания огня. В основном, мы будем обсуждать линзы, образованные сферическими поверхностями. Одна из поверхностей может быть плоской. Линзы бывают собирающими (положительными) и рассеивающими (отрицательными). Различить их можно наощупь, и даже в темноте, если принять к сведению общее свойство: любая линза отклоняет свет в сторону более широкой (более толстой) части. Кстати, призма на рис. 3 поступила точно так же). Так что все собирающие линзы в центре – толще, чем по краям; а рассеивающие – наоборот, в центре тоньше, на периферии – толще. С помощью схемы рис.6 формулируем некоторые определения. Фокус собирающей линзы – это точка, в которой параллельные лучи, падающие на линзу, пересекаются после их преломления в линзе: 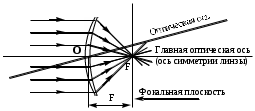 Рис. 6. Фокусирование света собирающей линзой. Главная оптическая ось линзы является ее осью симметрии – это прямая, проходящая через центры кривизны поверхностей линзы. Оптический центр линзы - точка О, находящаяся на главной оптической оси в центре линзы. Оптическая ось – это любая прямая, проходящая через оптический центр линзы; одна из них – главная оптическая ось, другие оси могут называться побочными или вспомогательными. Главный фокус линзы – точка F, в которой световые лучи, параллельные главной оптической оси, пересекаются после прохождения линзы. На рис. 5 показан именно главный фокус. Фокусное расстояние F линзы – это расстояние от оптического центра линзы до ее главного фокуса. Для собирающих (положительных) линз F > 0 (рис. 6); для рассеивающих (отрицательных) F ˂ 0 (см. рис. 9). Оптическая сила D линзы – величина, обратная фокусному расстоянию: D = 1 / F. Единица измерения – диоптрия (дптр). Оптическую силу D = 1 дптр имеет собирающая линза, фокусное расстояние которой F = 1 м. Оптическая сила рассеивающих линз - величина отрицательная. Тонкая линза – это линза, толщина которой пренебрежимо мала в сравнении с ее фокусным расстоянием. Световой луч, проходящий через оптический центр тонкой линзы, не меняет своего направления. Участок линзы в малых окрестностях оптического центра подобен плоскопараллельной стеклянной пластинке, в которой происходит лишь параллельное смещение дважды преломленного луча (рис. 7). В тонких линзах величиной этого смещения можно пренебречь. 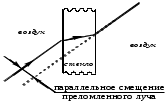 Рис. 7. Преломление света в плоской пластинке. Фокальная плоскость - плоскость, проходящая через главный фокус F линзы перпендикулярно главной оптической оси. Лучи, параллельные побочной оптической оси, после прохождения линзы сфокусируются в побочном фокусе – в точке F′ пересечения побочной оптической оси с фокальной плоскостью. Это иллюстрируется на рис. 8. 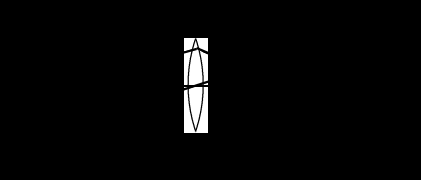 Рис. 8. Нахождение побочного фокуса F′. Если лучи, параллельные главной оптической оси, направлены на рассеивающую линзу (рис.9), то на выходе из линзы получается расходящийся поток лучей. 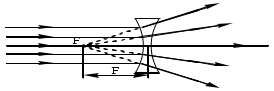 Рис. 9. Мнимый фокус рассеивающей линзы. Наблюдатель, находящийся справа от линзы, в расходящихся лучах, будет уверен, что лучи исходят из точечного источника, находящегося в точке F. 6. Линзы: построение изображений. Чтобы построить изображение любой точки S, достаточно найти точку пересечения любых двух лучей, исходящих из этой точки. Один из удобных лучей - луч, проходящий через оптический центр линзы: проходя линзу, он не меняет своего направления (луч 1 на рис.10 и 11) Другой удобный луч – это луч (2), параллельный главной оптической оси. 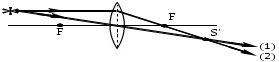 Рис. 10. В точке S′ - действительное изображение точки S 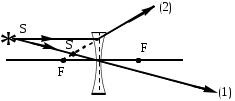 Рис. 11. В точке S′ - мнимое изображение точки S. При желании, можно направить на линзу любой интересный для нас луч и проследить его дальнейший ход. Для этого, сознавая, что он параллелен какой-нибудь побочной оси, построить эту параллельную ему ось, и далее следовать логике схемы рис. 8. Примечания: На схемах рисунков 10 и 11 точки фокуса F равноудалены от линзы слева и справа. Это верно лишь в тех случаях, когда показатели преломления среды слева и справа от линзы одинаковы. 2. Собирающую линзу можно использовать в качестве лупы. Для этого надо, чтобы изучаемый мелкий предмет находился от линзы на расстоянии меньше фокусного (рис. 12). Лупа даёт прямое увеличенное мнимое изображение. 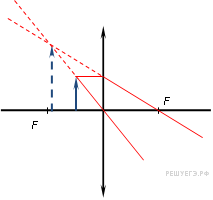 Рис. 12. Работа собирающей линзы в качестве лупы. 7. Ход лучей в оптическом микроскопе. Оптическая система микроскопа (рис. 13) состоит из двух собирающих линз: объектива и окуляра. Изучаемый объект В расположен левее левого фокуса объектива. Для получения изображения объекта В достаточно получить изображение В′′ его верхней точки. 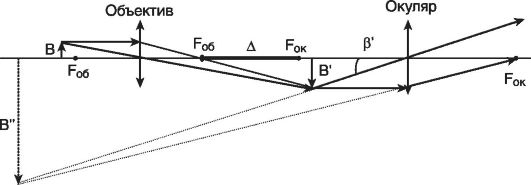 Рис. 13. Ход лучей в оптическом микроскопе. Действительное увеличенное изображение В′ объекта, созданное объективом, получено на пересечении двух «удобных» лучей, подобно тому, как это было на рис. 10. В точке их пересечения сходятся не только «удобные», но и любые другие лучи, исходящие из верхней точки объекта. В том числе и те два луча, которые являются «удобными» для построения изображения В′′, получаемого с помощью окулярной линзы. Действительное изображение В′, созданное объективом, дополни тельно увеличивается линзой окуляра, работающей в режиме лупы, подобно схеме рис. 12. На выходе оптической системы микроскопа – расходящиеся лучи, которые являются входными для оптической системы глаза наблюдателя. Преломляющие среды глаза формируют на сетчатке действительное изображение изучаемого объекта. А мозг воспримет изображение, полученное на сетчатке как изображение В′′. 8. Характеристики микроскопа. Линейное увеличение микроскопа указывает, во сколько раз микроскоп увеличивает изучаемый объект, и равно отношению размеров изображения, созданного микроскопом, к размерам изучаемого объекта: Гм = В′′/ В (*) Линейное увеличение объектива равно отношению размера созданного им изображения к размеру объекта: Гоб = В′ / В (**) Линейное увеличение окуляра равно отношению размера изображения В′′, созданного окуляром,к размеру изображения В′, созданного объективом: Гок = В′′/ В′ (***) Линейное увеличение микроскопа равно произведению линейных увеличений объектива и окуляра: Гм = Гоб · Гок . Убедиться в этом можно простой подстановкой в эту формулу выражений (**) и (***). Увеличение микроскопа как функция основных характеристик объектива и окуляра: Гм = a0 Δ / Fоб · Fок. (2) В формуле (2): Fоб, Fок – фокусные расстояния объектива и окуляра; Δ – оптическая длина тубуса микроскопа - расстояние между задним фокусом объектива и передним фокусом окуляра (см. схему рис. 13); а0 - расстояние наилучшего зрения; для нормального глаза а0 = 250 мм. Из формулы (2) следует, что чем меньше Fоб и Fок, тем больше увеличение микроскопа. Изготовить короткофокусный объектив или окуляр состоящими из одиночных линз, и получать при этом изображение высокого качества, оказалось невозможным. В современных оптических микроскопах объективы и окуляры – это сложные оптические системы, состоящие из нескольких линз. Но не только технические трудности изготовления тормозят прогресс. Главный ограничитель для роста величины увеличения – явление дифракции. От микроскопа требуется не просто многократное увеличение изучаемого объекта, но и точное воспроизведение его деталей. Предел разрешения Z микроскопа – это наименьшее расстояние между двумя точками объекта, которые различимы в поле зрения микроскопа как две раздельные. Величину Z иногда называют просто –разрешение. Для оценки способности прибора различать близкие точки предмета применяется похожая по названию, конкурирующая характеристика: разрешающая способность– величина, обратная разрешению. Чем меньше предел разрешения, тем больше разрешающая способность. Лучи света, которые создают в микроскопе изображение малого изучаемого объекта (на рис.14 –лучи от предмета), попадают в объектив из телесного угла U, который называется угловой апертурой.  U – угловая апертура объектива - это угол между крайними лучами светового потока, падающего на объектив от изучаемого предмета. 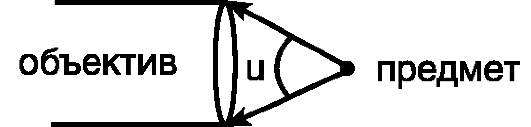 Рис. 14. Угловая апертура U. Предел разрешения микроскопа зависит только от свойств объектива микроскопа. Его можно определить по формуле Эрнста Аббе, основоположника современной теории микроскопов: Z =λ / 2 n Sin (U/2) (3) Здесь Z – предел разрешения; λ – длина волны света, которым освещается объект на предметном столике микроскопа; n - показатель преломления среды, в которой свет идет от предмета на объектив; U – угловая апертура объектива. У современных микроскопов апертура достигает значения U = 140°. Полагая n = 1 (воздушная среда) и λ = 555 нм (преобладающая длина волны в солнечном спектре), получаем по формуле (3) предел разрешения данного микроскопа: Zм = 300 нм. (4) Благодаря дифракции света, отдельные точки объекта на изображении будут выглядеть круглыми пятнышками, но не точками в математическом смысле. Если расстояние между двумя точками объекта больше. чем 300 нм, они будут на изображении как два раздельных, различимых пятнышка. Если между ними ровно 300 нм, то это - предельный случай: два пятнышка на изображении соприкасаются, но еще различимы как два объекта. Если же расстояние между точками меньше, чем 300 нм, то на изображении пятнышки сольются в один объект изображения. Дифракция характерна для волн любой физической природы. Законы геометрической оптики тоже применимы для волн любой природы, в пределах, допускаемых дифракцией. Для получения минимального значения предела разрешения Z формула (2) предписывает максимальное значение угловой апертуры U. Мы заложили в расчет достаточно большое достигнутое значение U = 140°. Предельным можно считать значение U = 180°, при котором Sin (U/2) = 1. С помощью формулы (2) получаем выражение: |
