ФИЗИКА Пraktikum. Учебнометодическое пособие для студентов медицинских вузов 2018 Вводное занятие
 Скачать 4.99 Mb. Скачать 4.99 Mb.
|
|
3.3. Слагаемое ρV2 / 2 – динамическое давление. У большинства это выражение ассоциируется с выражением для кинетической энергии: mV2 / 2. Ассоциация вполне уместная: динамическое давление – это кинетическая энергия единицы объема жидкости, имеющей скорость V. Главная особенность динамического давления состоит в том, что оно не является давлением в привычном смысле: оно не давит на стенки сосуда и на предметы, которые поток обтекает. Но оно проявит себя во всех своих паскалях при торможении потока: то, что до торможения было динамическим давлением, станет при торможении давлением статическим, действующим на остановившую поток преграду. В остановленном потоке динамическое давление равно нулю. Вот пример проявления динамического давления. При измерениях артериального давления наблюдаются колебания стрелки манометра в такт с турбулентными шумами, которые прослушиваются на локтевом сгибе при «засечке» систолического давления. Они возникают в связи с появлениями и исчезновениями просвета в артерии, сжатой манжетой, при прохождении пульсовой волны. Кровь в просвете артерии, возникающем в моменты систолы, имеет большую скорость (порядка 4 м/с). Кратковременное появление динамического давления приводит, в соответствии с уравнением Бернулли, к кратковременному уменьшению статического давления крови на стенку артерии. Это повторяется при каждом сердечном сокращении. Стрелка манометра отслеживает пульсации статического давления. При этом максимальное давление крови в систоле – это тот максимум, который успевает показать колеблющаяся стрелка манометра и который следует записать как систолическое давление в протокол измерений. В уравнении Бернулли (3) p0 – полное давление на участке гидравлической сети. Мы убедились, что все три слагаемых полного давления имеют смысл различных видов механической энергии единичного объема текущей жидкости. Тогда полное давление – это полная механическая энергия единицы объема текущей жидкости, и энергетический смысл уравнения Бернулли предельно прост: полная механическая энергия стационарного потока жидкости есть величина постоянная, если потери энергии на преодоление сил трения пренебрежимо малы. Подчиняясь условиям течения, слагаемые величины p0 могут меняться, но непременно так, чти их сумма будет оставаться постоянной. В качестве примера полезности уравнения Бернулли, рассмотрим особенности статического давления в гидравлической линии постоянного поперечного сечения, представленной на рис. 3. Ее участки находятся на различной высоте. 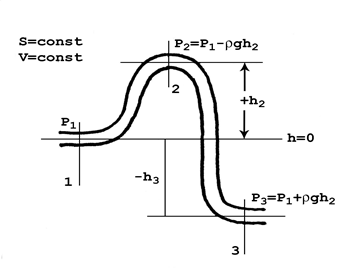 Рис.4. К уравнению Бернулли. Положим, что какой-то насос поддерживает в сечении 1 постоянное статическое давление p1. Так как площадь сечения сети постоянна, то скорость V и динамическое давление ρV2/2 тоже постоянны. Тогда уравнение Бернулли для участка между сечениями 1 и 2 запишется: p1 + ρV2 / 2 + 0 = p2 + ρV2 / 2 + ρgh2 Здесь в левой части – полное давление в сечении 1, а в правой – в сечении 2. После сокращения одинаковых значений динамических давлений, получаем: p1 = p2 + ρgh2 Отсюда следует: p2 = p1 - ρgh2, то есть p2 ˂ p1 . Аналогично, для участка между сечениями 1 и 3 после сокращений уравнение Бернулли принимает следующий вид: p1 = p3 - ρgh3, Отсюда следует:  Заголовок на боковой панели] [Боковые примечания — отличный способ вынести наиболее важные моменты из текста или разместить дополнительную информацию, чтобы ее можно было быстро найти (например, расписание). Их можно располагать слева, справа, в верхней или нижней части страницы или перетаскивать в любое другое место. Если вы готовы добавить свой текст — просто щелкните здесь и введите его.] p3 = p1 + ρgh3, то есть p3 > p1. Мы убедились, что статическое давление в приподнятых участках меньше, чем давление p1 на входе, а на опущенных – оно, наоборот, превосходит входное. Применительно к кровеносной системе: все, что находится выше уровня сердца, испытывает пониженное статическое давление (а это, в частности, мозг), а все, что ниже (ноги, например) -находится под давлением, превосходящим созданное сердцем. Для мозга действие гидростатического давления меняет статическое примерно на -30 мм рт. ст., а для ног эта «поправка» составляет около +110 мм рт. ст. Но система кровообращения имеет механизмы регулирования, вносящие поправки на снабжение кровью органов, находящихся в неравных условиях. Движение крови в реальной кровеносной системе сопровождается не постоянством (как у Бернулли), а постепенным уменьшением полного давления крови: энергия сердечного сокращения расходуется на преодоление сил вязкого трения и других сил сопротивления. На подходе к правому предсердию этот избыток давления, созданный левым желудочком, становится близким к нулю. Полное давление как сумма статического и динамического давлений, становится все меньше и наконец становится равным нулю: р0 = р + ρV2/2 = 0 Отсюда следует, что при достаточно большой скорости крови статическое давление может оказаться отрицательным: р = -ρV2/2 Этот результат означает, что давление в таких венах может быть несколько ниже атмосферного, и при их повреждении возможна воздушная эмболия – попадание воздуха в полости сердца. На реальном сердце такое статическое давление, которое можно называть разрежением, может составлять величину порядка - 3 мм рт. столба. Тонкостенные эластичные вены при этом временно спадают. 4. Режимы течения жидкостей. Различают два вида течения жидкостей: ламинарное и турбулентное. Ламинарное течение характерно для медленных потоков: это спокойное, упорядоченное движение. Перемешивание слоев чрезвычайно слабое: оно происходит лишь за счет молекул, совершающих тепловое хаотическое движение. В ламинарных потоках распределение скорости жидкости в поперечном сечении очень неравномерное: на рис. 5А мы видим сочетание медлительных пристеночных слоев с очень быстрым движением жидкости в ядре потока. Получается, что при ламинарном течении площадь поперечного сечения потока используется неэффективно: основная часть объемного расхода жидкости Q переносится в ядре потока, площадь которого невелика. 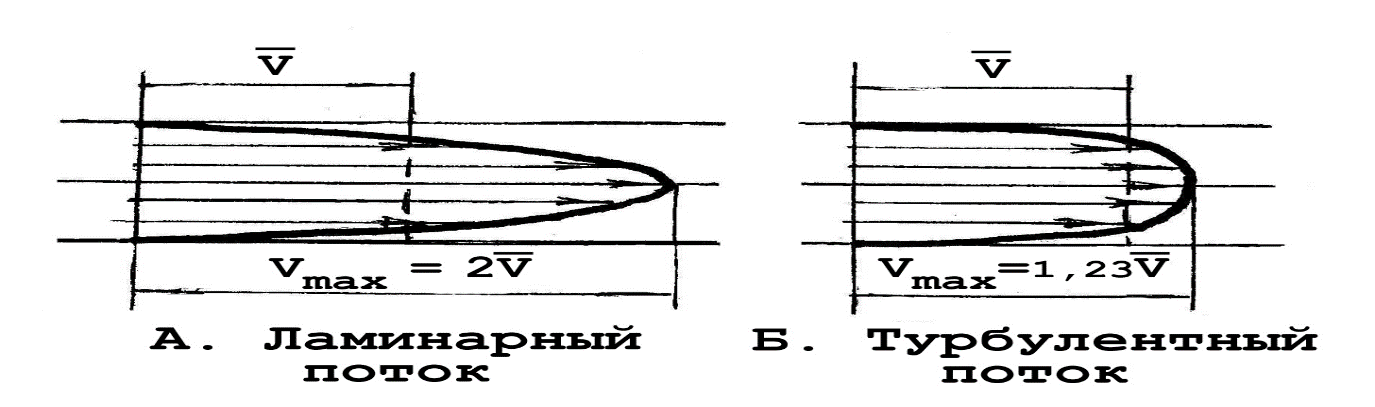 Рис. 5. Особенности ламинарного и турбулентного потоков. Турбулентное течение (от лат. turbulentus - беспорядочный) характерно для быстрых потоков. Взаимодействие соседних слоев турбулентного потока очень интенсивное: на границах слоев возникают временные образования – вихри различного масштаба. Вихри способствуют интенсивному перемешиванию жидкости и выравниванию скоростей в поперечном сечении потока: распределение скоростей становится ближе к равномерному (рис. 5 Б), что способствует росту пропускной способности трубопровода или кровеносного сосуда. Но за все приходится платить: появление турбулентных вихрей в потоке крови – это появление дополнительного вида движения в ней, на которые необходимы дополнительные затраты энергии работающего сердца. Турбулентные потоки сопровождаются шумами. Совокупность возникающих-исчезающих вихрей приводит к появлению пульсаций статического давления, действующего на стенки сосуда. Звуки, созданные турбулентными вихрями крови в артерии, прослушиваются через фонендоскоп при измерении артериального давления по методу Короткова. Переход от ламинарного режима к турбулентному происходит, если поток достигает некоторого критического значения скорости. Экспериментально установлено, что критическая скорость Vкр прямо пропорциональна динамической вязкости жидкости η и обратно пропорциональна плотности жидкости ρ и диаметру d сосуда: Vкр ̴ η / ρ d Изучение связи этих четырех показателей при ламинарном и при турбулентном режиме течения привело к созданию безразмерного критерия – числа Рейнольдса, которое можно назвать индикатором режима течения жидкости. 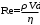 (4) (4)Здесь ρ - плотность жидкости; η - динамическая вязкость; V – средняя скорость жидкости в рассматриваемом сечении потока; d – диаметр сосуда в этом сечении. Как пользоваться этим индикатором? Надо вычислить по формуле (4) значение числа Рейнольдса Re для условий рассматриваемого потока и полученный результат сравнить с критическим значением числа Рейнольдса для данной жидкости – величиной Reкр . При Re ˂ Reкр условия в потоке соответствуют ламинарному режиму. При Re > Reкр в потоке установится турбулентный режим. Для различных жидкостей значение Reкр различно. Для воды Reкр = 2300. Для крови Reкр = 970 ± 80. Повод для размышлений: в кровеносном сосуде диаметром 2,5 мм значение Reкр достигается при скорости движения крови около 4 м/с. Вопрос: каким станет режим течения в этом кровеносном сосуде, если увеличить любой один параметр правой части формулы (4)? Отметим, что для перевода режима течения жидкости из турбулентного в ламинарный требуется снижение скорости, при котором Re « Reкр. Это означает, что ламинарный режим течения легче разрушить, чем потом восстановить. Турбулентный режим может установиться при значениях числа Рейнольдса, гораздо меньших, чем критическое. Разрушителями ламинарного течения могут оказаться шероховатые стенки, резкие повороты потока, выступающие в поток элементы измерительных устройств. В кровеносных сосудах это могут быть склеротические бляшки на их стенках. В заключение отметим, что атмосферные циклоны и антициклоны – это вихри гигантского масштаба - проявления неустойчивости воздушных потоков в атмосфере нашей планеты. 5. Формула Пуазейля. Гидравлическое сопротивление. ОПСС. В тонких длинных трубках с ламинарным режимом течения жидкости выполняется соотношение, полученное Пуазейлем и Стоксом и известное как формула Пуазейля: 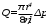 (5) (5)Здесь Q – объемный секундный расход жидкости, (м3/с); Δр – перепад давлений на трубке: ∆р = рвх – рвых , (Па); l – длина трубки, (м); r – ее радиус, (м); η - динамическая вязкость жидкости, (Па·с). Формула фиксирует важную причинно-следственную связь объемного секундного расхода жидкости Q и перепада давления Δр на трубке. Даже если давление на концах трубки очень большое, но одинаковое, то ∆р = 0, и течение жидкости в трубке не возникнет, но чем больше Δр, тем больше Q. и чтобы выделить значимость этой связи, формулу Пуазейля часто применяют в виде: 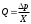 , где , где 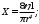 (6) (6)Здесь Х – гидравлическое сопротивление трубки, учитывающее внутренний радиус трубки, ее длину и динамическую вязкость протекающей по ней жидкости. Особо заметен в формуле гидравлического сопротивления множитель r4: влияние радиуса сосуда на его гидравлическое сопротивление чрезвычайно сильное. К примеру, если радиус r изменить в два раза, то величина r4 изменится в 16 раз! В 16 раз изменится и гидравлическое сопротивление сосуда. Это влияние проявляется, в частности, при развитии гипертонического криза – тяжелого состояния, вызванного чрезмерным повышением артериального давления. При развитии криза имеет место следующая цепочка событий в кровеносной системе: сбой в системе сосудистой регуляции → спазм артериол (то есть уменьшение их радиуса) → повышение их гидравлического сопротивления → повышение частоты сердечных сокращений → резкий рост артериального давления → дополнительная нагрузка на систему сосудистой регуляции → дополнительный спазм, и т д. – круг замкнулся, система пошла вразнос. Как первоочередная мера при подобных состояниях – применение спазмолитиков – препаратов, снимающих спазмы и обладающих сосудорасширяющим действием (коньяк и др.). Формула Пуазейля имеет полезное алгебраическое следствие: Х = 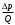 (7) (7)Это выражение можно использовать для экспериментального определения величины гидравлического сопротивления Х реального кровеносного сосуда. В гемодинамике формула (7) нашла применение для ͞оценки гидравлического сопротивления большого круга кровообращения. В кардиохирургии этот важный показатель состояния сердечно-сосудистой системы принято называть так: общее периферическое сопротивление сосудов (ОПСС) и оценивать по формуле: ОПСС = 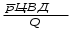 (8) (8)Здесь Q – общий объем кровотока; ͞p - среднее артериальное давление: ͞p = рд + 1/3 ( рс - рд ) ЦВД – центральное венозное давление – то есть давление в правом предсердии; в норме это 6 -12 мм рт. столба. Пример вычислений. При артериальном давлении 120 / 80 мм рт. столба давление: ͞p–ЦВД = 93,3–9 мм рт. ст.=84,3мм рт. ст.·(133Па/мм рт. ст.)= =11,2·103Па. Полагая Q = 80 мл /с = 0,08 л/с, получаем ОПСС = 140 кПа·с /л. В норме ОПСС - в пределах 80 – 150 кПа·с /л. ОПСС не может быть непосредственно измеренным; во всяком случае в настоящее время это – так. В то же время повсеместно отмечается важность и ценность этого показателя. Из формулы (8) следует, что чем больше артериальное давление, тем больше ОПСС, и наоборот. Но экспериментальные исследования показывают, что эта простая линейная связь может нарушаться: в правой части формулы (8) есть не только числитель, но и знаменатель. Выше, в примере вычислений ОПСС, величина Q была принята на уровне среднестатистической нормы и молчаливо полагалась величиной постоянной. Но это, как выясняется, не всегда так. В заключение этого параграфа – предложение для продвинутых студентов: рассмотреть аналогию между формулой Пуазейля и законом Ома для участка электрической цепи. Что на что похоже? Глубока или поверхностна эта аналогия? И вообще… Свойства кровеносных сосудов. Кровеносные сосуды подразделяются на четыре типа: артерии эластичного типа, артерии мышечного типа, капилляры и вены. 6. Артерии эластичного типа - крупные кровеносные сосуды, находящиеся в непосредственной близости от сердца. Стенки таких сосудов содержат значительное количество эластических волокон. Эластичность – способность стенок к растяжению при возрастании давления крови – сочетается с большой прочностью: стенки способны выдерживать давление, десятикратно превосходящее нормальное систолическое. Прочность стенок достигается тем, что в них, помимо эластических, имеется значительное количество коллагеновых волокон, отвечающих за прочность. Однако прочностные способности таких волокон проявляются лишь при значительных деформациях стенок. Это объясняется рыхлой укладкой волокон; они как бы спутаны, и начинают проявлять прочность, распрямившись при больших деформациях стенок. Кровоток в аорте и в артериях имеет пульсирующий характер. При сокращении желудочков происходит резкий выброс ударного объема крови (УО равен 60 – 100 мл). Механическая энергия выброса преобразуется следующим образом: • часть энергии выброса становится потенциальной энергией больших и малых артерий: они слегка расширяются, напрягаются, и в таком состоянии они – аккумуляторы давления крови. Упругие силы в стенках постепенно возвращают сосуды к первоначальному диаметру, поддерживая равномерный кровоток в артериолах и капиллярах на протяжение периодов диастолы; • оставшаяся часть общей энергии переходит в кинетическую энергию движущейся крови; благодаря эластичности сосудов, возникает и распространяется пульсовая волна. 7. Пульсовое давление – это разность между систолическим и диастолическим давлением. Эта разность давлений возникает при каждом сердечном сокращении и ощутима под пальцами (то есть при пальпации) на артериях, расположенных близко к поверхности тела: на лучевой, сонной, бедренной. Опытный врач по тактильным ощущениям пульса способен оперативно высказать весьма весомые суждения о состоянии сердечно- сосудистой системы своего пациента. 8. Сфигмография (от греч. sphigmos – пульс) – метод графической регистрации артериального пульса. Регистрируется p(t) - давление крови в артерии как функция времени, в том месте артерии, над которым установлен датчик. Устанавливается он с легким прижатием к поверхности тела, то есть так, чтобы датчик воспринимал пульсации давления, но не нарушал при этом кровотока. Хорошо воспроизводят пульсации давления крови в артерии пьезоэлектрические датчики. Электрический сигнал датчика подается на усилитель, а с его выхода – на регистрирующее устройство. В качестве регистрирующего устройства может использоваться электрокардиограф. В этом случае можно обойтись и без дополнительного усилителя. Результатом сфигмографии является сфигмограмма – график зависимости p(t) - давление крови в артерии как функция времени. На рис. 6 представлены сфигмограммы двух пациентов разного возраста. Единичный цикл сфигмограммы в увеличенном масштабе – на рис. 7.  Рис. 6. Сфигмограммы; возраст 22 года (слева) и 62 года (справа). На рис. 7 представлен типичный цикл сфигмограммы. Точкам c и h этой кривой соответствует диастолическое давление в артерии; точке d – систолическое. С помощью этого графика рассмотрим особенности функционирования кровеносных сосудов при сердечном сокращении и стадии формирования пульсовой волны.  Рис. 7. Цикл сфигмограммы сонной артерии. |
