ФИЗИКА Пraktikum. Учебнометодическое пособие для студентов медицинских вузов 2018 Вводное занятие
 Скачать 4.99 Mb. Скачать 4.99 Mb.
|
|
5. Точность. Абсолютная и относительная погрешность измерений. Точность измерений – качественная оценка близости результата измерений к истинному значению измеряемой величины. Эта интуитивно понятная категория не имеет своих собственных количественных показателей и поэтому пользуется чужими: абсолютной и относительной погрешностью измерений. Истинное значение измеряемых величин определить невозможно. Причин тому – великое множество; в каждом конкретном случае находится группа факторов, ограничивающих точность. Так что погрешности измерений неизбежны, и обязательным этапом любого измерения должна быть их количественная оценка. Факторы, приводящие к появлению погрешностей, укрупненно, могут быть связаны с особенностями исследуемого объекта, со свойствами измерительного прибора, с качествами экспериментатора. Процедуры любых медицинских измерений жестко регламентированы до мелочей (измерение артериального давления, снятие ЭКГ, и т.п.). Эти регламенты нужны, чтобы исключать возможное появление каких-нибудь дополнительных причин погрешностей. Абсолютная погрешность Δх – это отклонение результата измерения х от истинного значения измеряемой величины: Δх = х – хист. Абсолютная погрешность Δх имеет ту же размерность, что и величина х. Если вдуматься, предложенное определение абсолютной погрешности – предел совершенства; лучше – не придумаешь. Но если вдуматься еще глубже, толку от этого определения маловато, меньше, чем хотелось бы, поскольку истинное значение хист нам не известно и не будет известно никогда. Величину абсолютной погрешности приходится определять опосредованно, обходными путями. Кое-что вам знакомо из курса математической статистики. Но и она не всесильна. Некоторые методы оценки абсолютной погрешности измерений. 1. Принцип цены наименьшего деления. Школьная линейка имеет шкалу, разбитую на сантиметры и миллиметры. Цена наименьшего деления линейки – 1мм. Следовательно, измерения размеров тел с помощью такой линейки могут производиться с абсолютной погрешностью Δх ==1мм. Форма записи результата измерений (пример): L = 195±1 мм. Производители измерительной техники изготавливают шкалы приборов так, чтобы цена деления соответствовала абсолютной погрешности. 2. Абсолютную погрешность прибора можно определить с помощью другого прибора, имеющего более высокую точность измерений. 3. При проведении многократных повторных измерений, чем больше число измерений, тем меньше абсолютная погрешность средневыборочного результата. 4. Абсолютную погрешность измерений, выполняемых прибором, легко определить, если есть информация о классе прибора. Эта информация может быть указана в техническом паспорте прибора; иногда класс прибора К указан на шкале прибора, где-нибудь с краю. Согласно ГОСТ 8.401-80, класс К обозначается одним из чисел следующего числового ряда: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01. Абсолютная погрешность для результата измерения х : Δх = ± К‧хmax / 100 Пример вычислений по этой формуле: миллиамперметр класса К=0.5, предназначенный для измерения токов до Imax = 250 мА, показал силу тока I = 180 мА. Абсолютная погрешность при этом: ΔI = 0,5‧250 / 100 = 1,25 мА. Результат измерений: I = 180±1,25 мА. Правильнее записать этот результат с округлением до единиц младшего разряда результата 180, то есть считать окончательным результатом запись I = 180±1 мА. Относительная погрешность δх результата измерений – это отношение абсолютной погрешности Δх к величине xрезультата измерения: δх = Δх / х (2) Относительная погрешность – величина безразмерная. Поскольку, как правило, Δх ‹‹ х, относительную погрешность обычно выражают в процентах. Например, результату измерений I = 180±1 мА соответствует относительная погрешность δI = 1 / 180 = 0,00555 = 0,56% Относительную погрешность удобно использовать для сопоставления точности измерений, выполняемых разными методами; измерений, выполняемых в разных диапазонах измеряемой величины и даже для сравнения точности измерения разных физических величин. 6. Результаты измерений в категориях математической статистики. С точки зрения теории вероятностей величина, которая при измерениях не может быть установлена точно, может рассматриваться как случайная величина, и может анализироваться методами теории вероятностей и математической статистики, знакомыми вам по математическому блоку курса «Физика, математика». Вместе с тем, измерения – это вид деятельности, имеющий многовековую историю, сложившийся круг понятий и методов. Вам остается убедиться, что недавно изучавшаяся вами математическая статистика и традиционная теория измерений хорошо дополняют друг друга. Если бы идеально точные измерения были возможны, то каждый результат такого измерения можно бы представить, как точку, положение которой на числовой оси твердо установлено и сомнениям не подлежит. В реальных измерениях результат измерений – это некоторый интервал х±Δх (от х-Δх до х+Δх), в котором содержится истинное значение измеряемой величины – доверительный интервал. Доверительный интервал задается в привязке к результату х состоявшегося измерения. Если провести повторное измерение, доверительный интервал может измениться. Утверждение о том, что истинное значение измеряемой величины содержится в обсуждаемом интервале, справедливо лишь с некоторой вероятностью Р, которая называется доверительной вероятностью. Величина α = 1 – Р – уровень значимости – вероятность того, что истинное значение измеряемой величины не содержится в доверительном интервале. Проведение повторных измерений приводит к уменьшению ширины доверительного интервала или к уменьшению уровня значимости и увеличению доверительной вероятности; выбор при этом – за экспериментатором. Указания, как определять границы доверительных интервалов, приведены в данном пособии в описаниях лабораторных работ всюду, где это необходимо. 7. Систематические и случайные погрешности. Систематические погрешности – это погрешности, вызываемые факторами, действующими постоянно (т.е. систематически). Их можно обнаружить и измерить с помощью более точных приборов. Прибор, дающий систематическую погрешность, всегда завышает или всегда занижает свои показания, то есть во всех измерениях значения абсолютной погрешности – это числа одного знака. Но по модулю она может быть от случая к случаю различной. Причины появления систематических погрешностей могут быть тривиальными (например, разрядилась батарейка), а могут быть и более коварными (непостоянство диаметра капилляра в термометре; несовершенство методики косвенных измерений). Количество возможных причин может исчисляться десятками. Единой методики выявления причин появления систематических погрешностей не существует. Вопрос для быстро соображающих: какие неожиданности грозят автомобилисту, если он контролирует расход топлива по показаниям уровнемера, а бензобак сужается книзу? Какую погрешность имеет уровнемер? Если систематическая погрешность обнаружена и оценена количественно, то возможны следующие варианты действий: - устранение ее причины; - коррекция показаний состоявшихся и будущих измерений на величину систематической погрешности; - пренебрежение систематической погрешностью, если она достаточно мала. Случайные погрешности - результат несогласованного действия группы факторов, среди которых нет доминирующих по влиянию на общий результат. Случайные погрешности имеют следующие свойства: 1. Одинаковые по модулю положительные и отрицательные погрешности равновероятны. 2. Меньшие по модулю погрешности встречаются чаще, чем большие. 3. С увеличением числа измерений одной и той же величины, среднее арифметическое значение случайных погрешностей, посчитанное с учетом их знаков, стремится к нулю. Это означает, что с ростом количества измерений среднеарифметическое значение результатов измерений стремится к истинному значению измеряемой величины. Свойство 3 - кардинальный способ уменьшения величины случайных погрешностей - увеличение количества измерений. Случайные и систематические погрешности могут спокойно сосуществовать друг с другом. 8. Нормальный закон распределения в экспериментальных исследованиях. Случайные величины, обладающие свойствами 1 – 3 предыдущего раздела, можно сказать, предрасположены к тому, чтобы иметь распределение вероятности, известное как распределение Гаусса (нормальный закон распределения). По нормальному закону распределено очень многое в самых разнообразных областях знаний. Универсальность нормального закона сумел обосновать А.М. Ляпунов. Согласно его теореме, если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин х1, х2, …, хn, влияние каждой из которых на всю сумму ничтожно мало՜, то независимо от того, каким законам подчиняются слагаемые х1, х2, …, хn, сама величина Х будет иметь распределение вероятностей, близкое к нормальному, и тем точнее, чем больше число слагаемых n. Человеческий организм – сложнейшая система; количество показателей жизнедеятельности – громадное; количество их возможных связей друг с другом – еще больше. Требование теоремы Ляпунова о том, чтобы влияние каждого из них на всю сумму было ничтожно малым, может быть выполнено в одних исследованиях и не выполненным - в других. В ходе любого медико-биологического эксперимента, накопив выборку результатов измерений некоего параметра, имеет смысл проверить ее на соответствие нормальному закону распределения, применив подобающий случаю статистический критерий (Шапиро-Уилка, Пирсона). При этом, любой результат проверки по-своему интересен. Если гипотеза о нормальном распределении принимается, вы получаете возможность применить к этому параметру все свои познания о свойствах нормально распределенных величин. Если же гипотеза не принимается, вы приходите к выводу, что среди множества факторов, влияющих на исследуемый параметр, есть доминирующие по влиянию, и их неплохо бы выявить; и это уже – призыв к действиям в нужном направлении. Что касается применимости нормального закона к погрешностям измерений, то если систематические погрешности устранены (или вычтены из результатов измерений), то по опыту исследований погрешностей в измерительных системах, оставшиеся случайные погрешности распределены по нормальному закону или очень близки к нему. Контрольные вопросы по теме «Вводное занятие». 1. Измерения. Основные единицы системы СИ. 2. Производные единицы системы СИ для частоты, силы, давления, энергии, мощности. 3. Производные единицы системы СИ для электрических и магнитных величин: заряд, потенциал, сопротивление, электроемкость, магнитная индукция, поток магнитной индукции, индуктивность. 4. Некоторые внесистемные единицы: миллиметр ртутного столба, калория, электронвольт, лошадиная сила. 5. Дробные и кратные единицы. 6. Прямые и косвенные измерения. Примеры. 7. Абсолютная и относительная погрешность измерений. Методы оценки абсолютной погрешности. 8. Доверительный интервал. Доверительная вероятность. Уровень значимости. 9. Систематические погрешности, их происхождение, свойства, способы выявления и уменьшения. 10. Случайные погрешности, их происхождение, свойства, способы выявления и уменьшения. 11. Нормальный закон распределения: причины его универсальности; применение в эксперименте. Материалы к лабораторной работе №51 и к семинару по биоакустике В этом разделе вам предстоит систематизировать представления о колебаниях и о волновых процессах. Здесь рассматривается система характеристик колебаний и волн, применительно к звуку. Но надо иметь в виду, что большинство понятий и идей, обсуждаемых в акустических разделах пособия, универсальны, и применимы в различных областях. 1. Колебания. Их характеристики. Гармонические колебания. Колебания – это процессы, характерные той повторяемостью во времени. По физической природе колебания могут быть механическими, электромагнитными, смешанного типа. Простейший пример механической колебательной системы - грузик, качающийся на нити. Воспользуемся этой легко представимой системой, чтобы систематизировать сведения о колебаниях как таковых, об их общепринятых характеристиках и единицах их измерений. Свободные колебания - это колебания в системе, выведенной из состояния равновесия и предоставленной самой себе. Если грузик отклонить на нити и отпустить, начнутся его свободные колебания. Собственная частота (частота собственных колебаний) – это частота свободных колебаний в системе, В примере с грузиком она зависит от длины нити и от ускорения свободного падения в данной местности. Причины возникших колебаний: действие силы тяжести, инерция грузика и то, что мы, первоначально отклонив грузик, сообщили ему некоторую механическую энергию. Отпустив отклоненный грузик, мы предоставили ему возможность совершать свободные колебания. Однако свободные колебания грузика будут затухающими. Причины - потери энергии на преодоление сил сопротивления. Период колебаний Т - это длительность одного полного цикла колебаний. Периодические колебания характерны постоянством периода; пример - колебания грузика на нити. А вот колебания любых характеристик сердца (механических, электрических, магнитных) не являются строго периодическими даже при нормальной работе сердца. Частота колебаний ν- это количество колебаний в единицу времени. Частота обычно измеряется в герцах. Если колебания таковы, что за одну секунду происходит один их полный цикл, то их частота - 1 Гц. Для более частых колебаний применяются кратные герцу единицы: 1 кГц = 10 3 Гц; 1 МГц = 10 6 Гц; 1 ГГц = 10 9 Гц, 1 ТГц = 10 12 Гц. Частота и период взаимно обратны: ν = 1/Т; Т=1/ν. Что колеблется в примере с колебаниями грузика на нити? Прежде всего вспоминаются зрительные образы: происходит непрерывное изменение положения грузика в пространстве, с характерной для колебаний повторяемостью положений. Но это далеко не все, что колеблется в этом примере. Колебаниям подвержены горизонтальная и вертикальная координаты грузика, его скорость и ускорение, его кинетическая и потенциальная энергия, угол отклонения нити и сила ее натяжения. Этот перечень можно бы и продолжить. Гармонические колебания - это колебания, при которых характеризуемая величина y изменяется во времени t по закону синуса или косинуса: y = А sin ( ω t + φ0 ) или y = А cos ( ω t + φ0 ) (1) Здесь: А – амплитуда колебаний – наибольшее отклонение величины y от ее значения в положении равновесия системы (или от другой, более удобной, стадии колебаний); ω - так называемая циклическая частота; ее связь с обычной частотой: ω = 2πυ , то есть они отличаются друг от друга в 6.28 раза. (ωt + φ0) - фаза колебаний - величина, численно характеризующая стадию, в которой находится очередной цикл в любой момент времени t. В частности, при t =0 значение фазы равно φ0, и это - начальная фаза. На рис.1 показано ровно то, что значится в подписи к нему. Слева, на векторной диаграмме, показан амплитудный вектор А (его модуль равен амплитуде колебаний), образующий с горизонтальной осью x угол φ0, равный начальной фазе колебаний. Будем, напрягая воображение, равномерно вращать амплитудный вектор против часовой стрелки с постоянной угловой скоростью ω, равной циклической частоте колебаний. Проекция конца вектора A на ось y будет непрерывно меняться. На графике справа показана проекция вращающегося вектора А на ось y как функция времени t : y = A Sin ( ω t + φ0 ) 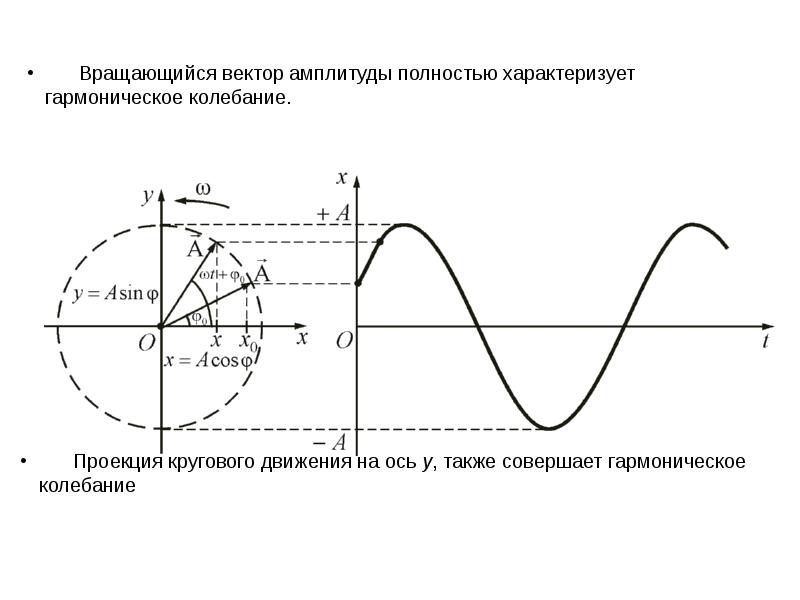 Рис. 1. Гармонические колебания как проекция равномерного вращения вектора А. Гармонические и близкие к ним колебания встречаются во многих областях знаний: механика, акустика, электромагнитные колебания. В любой из этих областей встречаются сложные колебания, которые при ближайшем рассмотрении оказываются суммой нескольких одновременно происходящих, наложившихся друг на друга простых гармонических колебаний различной частоты и амплитуды. На рис. 2 представлен пример подобного рода: сложный звук (кривая 4), возникший как сумма трех простых гармонических колебаний - гармоник. 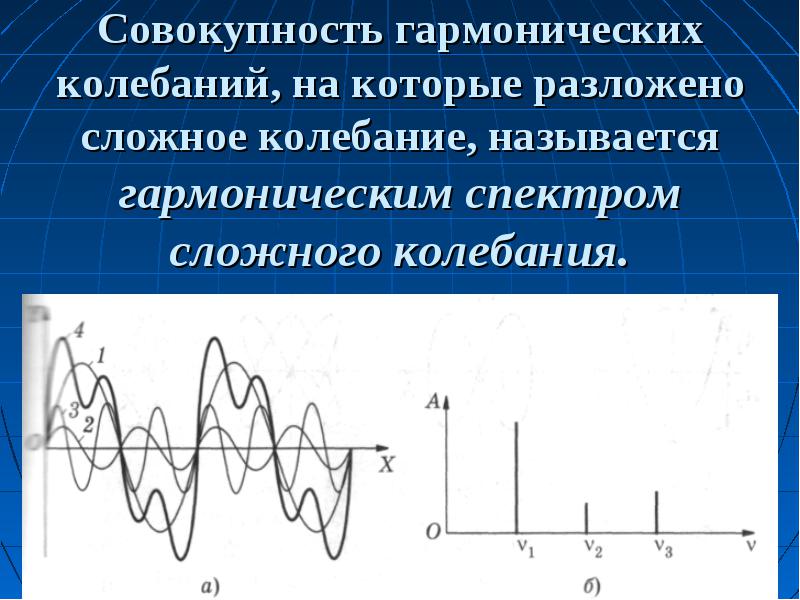 Рис.2.(a)-сложное колебание (кривая 4) как сумма трех гармоник; справа - гармонический спектр. Гармонический анализ – это разложение сложного колебания на простые слагаемые. Результатом гармонического анализа является спектр колебаний. Пример спектра приведен на рис. 2 б. Спектр колебаний - это диаграмма, показывающая, как распределяется общая энергия колебаний по различным значениям частоты. В частном случае, представленном на рис. 2 б, распределение энергии очень неравномерное: колебания происходят лишь на трех значениях частоты. К тому же, на этих частотах различна амплитуда А Спектр данного вида - линейчатый. Примечания: Чем больше амплитуда колебаний, тем больше их энергия. Более того, энергия колебаний пропорциональна квадрату амплитуды. Помимо линейчатых спектров, существуют спектры других типов: полосатые и непрерывные. В полосатых - вертикальные полосы вместо вертикальных линий. В непрерывных - отражается возможность одновременных колебаний на всех частотах широкого диапазона. Идея представления сложных колебаний в виде суммы нескольких гармоник различной частоты и амплитуды получила интересное развитие в математике, в теории приближения функций. Согласно этой теории, практически любая функция (в том числе - никак не связанная с колебаниями, и в том числе - заданная не формулой, а графиком, в том числе, графиком, полученным экспериментально или даже нарисованным прибором-самописцем); так вот, любая функция может быть приблизительно равна сумме некоторого количества гармоник. Такое представление функций, предложенное французским физиком и математиком Жаном Фурье, названо его именем: разложение Фурье. |
