ФИЗИКА Пraktikum. Учебнометодическое пособие для студентов медицинских вузов 2018 Вводное занятие
 Скачать 4.99 Mb. Скачать 4.99 Mb.
|
|
8. Вязкость крови в норме и при патологии. Относительная вязкость крови – это безразмерная величина, показывающая, во сколько раз вязкость крови превосходит вязкость воды при той же температуре. Этой внесистемной единицей воспользуемся для сопоставления различных состояний крови. Вязкость крови в норме составляет 4 – 6 относительных единиц. При патологиях наблюдаются отклонения как в большую, так и в меньшую сторону. Кровь повышенной вязкости, 7 - 20 единиц, называют густой кровью. Не трудно представить себе, насколько тяжелее сердцу перекачивать кровь, вязкость которой по тем или иным причинам возросла в четыре раза и стала в 20 раз больше, чем вязкость воды! Полноценное снабжение тканей и органов кислородом резко усложняется. Сердце вынуждено работать в форсированном режиме. Артериальное давление повышается. Дефицит кислорода ощущает и сердечная мышца. Возникает ощущение общей слабости, работоспособность падает, в частности, ухудшается работа мозга: рассеянное внимание, головокружение, возможно депрессивное состояние. При повышении вязкости возрастает опасность образования тромбов в кровеносных сосудах, а это может привести к сердечной недостаточности, инфаркту, инсульту. Кровь пониженной вязкости, 1 – 3 единицы, характерна пониженным содержанием форменных элементов, а объем плазмы возрастает - кровь становится более жидкой. Нарушается свертываемость крови. Даже пустяковая ранка может привести к большим кровопотерям. Возможны кровотечения из носа, десен, внутренних органов. 9. Формула Стокса. В предстоящей лабораторной работе вязкость жидкости определяется по скорости погружения шарика (метод Стокса). Плотность материала шарика должна быть больше, чем плотность жидкости, иначе он тонуть не станет. Случай равенства плотностей здесь не обсуждаем. Тонущие шарики заявлены в названии работы как модель оседающих в плазме крови эритроцитов. Насколько хороша эта модель, вам предстоит оценить. При движении твердого шарика в жидкости (или при обтекании неподвижного шарика потоком жидкости) возникает сила сопротивления, обусловленная вязким трением между слоями жидкости, огибающими шарик. Стокс установил, что эта сила сопротивления равна: Fc = 6ℼηrv (3) Здесь: r – радиус шарика; v – скорость его движения; η - коэффициент динамической вязкости жидкости. Этот результат известен как формула Стокса. В эту формулу входит вязкость жидкости, и она - в компании с величинами, сравнительно легко доступными для измерения. Благодаря этому формула Стокса - хорошая основа для метода измерения коэффициента вязкости η – метода Стокса. 10. Движение шарика в жидкости. При выполнении работы Вы будете наблюдать погружение пластиковых шариков в воде. Это погружение имеет две стадии. 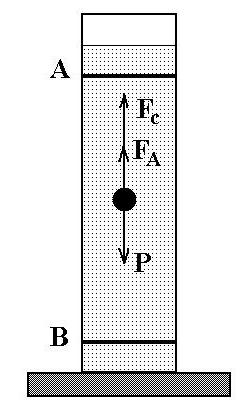 Первая стадия – ускоренное движение под действием преобладающей силы тяжести. Вертикально вниз направлена сила тяжести Р=mg шарика. Вертикально вверх на протяжении всего погружения шарика действует Архимедова сила FА; но FА ‹ mg, и шарик тонет, погружаясь все быстрее. Но чем быстрее он тонет, тем больше становится сила сопротивления Fc. Эта сила направлена в сторону, противоположную движению, т.е. вверх. Первая стадия – ускоренное движение под действием преобладающей силы тяжести. Вертикально вниз направлена сила тяжести Р=mg шарика. Вертикально вверх на протяжении всего погружения шарика действует Архимедова сила FА; но FА ‹ mg, и шарик тонет, погружаясь все быстрее. Но чем быстрее он тонет, тем больше становится сила сопротивления Fc. Эта сила направлена в сторону, противоположную движению, т.е. вверх.При достижении некоторой скорости равнодействующая всех трех сил, приложенных к шарику, становится равной нулю: mg - FА - Fc = 0. (4) Рис. 3. К методу Стокса. Вторая стадия – равномерное движение. Подчиняясь первому закону Ньютона, шарик движется равномерно и прямолинейно, с сохранением скорости, достигнутой на первом этапе. Для уравнения (4) запишем в развернутом виде все три его слагаемых mg = ρшVg Здесь ρш - плотность материала шарика, g-ускорение свободного падения, V-объем шарика. Из геометрии: V= 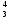 πr³, где r - радиус шарика. πr³, где r - радиус шарика.В итоге: mg = 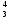 πr³ρшg πr³ρшg 2. По закону Архимеда FА=ρв Vg, где ρВ - плотность воды, окружающей шарик; В итоге: FА= 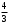 πr³ρв g πr³ρв g3.Слагаемое Fc описывается формулой Стокса. В окончательном итоге, уравнение (4) принимает следующий вид: 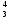 ℼr³ρшg - ℼr³ρшg - 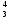 ℼr³ρв g - 6ℼηrv = 0 (5) ℼr³ρв g - 6ℼηrv = 0 (5) В этом уравнении радиус шарика и значения плотностей – величины известные, а множитель π и вовсе сокращается. Скорость равномерного погружения на втором этапе: v = s / t. Единственной неизвестной в уравнении (5) стала вязкость воды η. Решение уравнения (5) относительно η дает нам расчетную формулу данной лабораторной работы: η = 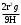 (ρш - ρв)‧t (6) (ρш - ρв)‧t (6)11. Порядок выполнения работы. 1. Измерить линейкой расстояние Н между двумя полосками А и В на сосуде с водой (см. рис. 3). В пределах перемещения Н происходит равномерное погружение шарика. 2. Наблюдать погружение шариков. Длительность t прохождения контрольного промежутка Н измерять с помощью секундомера мобильного телефона 3. Результаты измерений и вычислений заносить в таблицу 3. Вычисления коэффициента вязкости выполнить по формуле (6). Будьте внимательны: все величины должны быть в основных единицах системы СИ. Необходимые справочные данные приведены в табл. 4. Обратите внимание: в правой части формулы (6) всё, кроме времени t, можно вычислить однократно (заменить на постоянный множитель). Таблица 3. Результаты измерений и вычислений.
Таблица 4. Некоторые данные к вычислениям коэффициента вязкости.
4. Данные столбца 5 таблицы 3 - это выборка значений коэффициента вязкости объемом n = 5. Вычислить средневыборочное значение и границы доверительного интервала для коэффициента вязкости. Средневыборочное значение коэффициента вязкости: 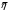 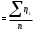 Отклонения от среднего: 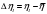 Дисперсия выборки: 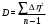 Среднеквадратичное отклонение: 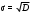 Ширина доверительного интервала: 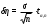 tα,n – коэффициент Стьюдента; α – уровень значимости. Значения коэффициента Стьюдента для условий данной работы приведены в табл. 5. Результаты работы представить в виде 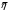 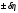 : :η = ______________(мПа‧с) на уровне значимости α =____ при t0С =_______ Табл. 5. Значения коэффициента Стьюдента.
12. Контрольные вопросы к лабораторной работе № 53. Эритроциты: строение, свойства и функции. Скорость оседания эритроцитов (СОЭ). Методы ее измерения. Диагностическая ценность СОЭ. Вязкость жидкостей. Формула Ньютона, Формула Стокса. Коэффициенты динамической и кинематической вязкости. Ньютоновские и неньютоновские жидкости. Вязкость крови. Относительная вязкость. Вязкость крови в норме и при патологии. Измерение вязкости по методу Стокса. Лабораторная работа №54. Работа с электрокардиографом. Построение средней электрической оси сердца. Цели работы: Ознакомление с основами метода электрокардиографии. Снятие ЭКГ в трех отведениях. Построение средней электрической оси сердца. 1. Электрография, ее виды. Электрокардиография. Электрография – метод исследования работы органов и тканей, основанный на регистрации во времени разности потенциалов, возникающей на поверхности тела при функционировании органов и тканей. Этот метод дает обширную информацию о работе различных органов и тканей. Сложилась группа злектрографических методов исследования различных органов и систем организма. Исторически первым в этой группе является метод электрокардиографии. Кроме того, применяются: - электроэнцефалография (ЭЭГ) – регистрация электрической активности мозга; - электромиография (ЭМГ) – регистрация электрических потенциалов мышц; - электроретинография (ЭРГ) – регистрация потенциалов сетчатки глаза; - электрическая активность кожи (ЭАК) – регистрация собственных потенциалов кожи или регистрация слабых токов от внешних источников; устаревшее название – кожно-гальваническая реакция (КГР). Электрокардиография (ЭКГ) – метод регистрации и исследования электрических полей, возникающих при работе сердца. Регистрируется некоторый суммарный эффект электрической активности клеток сердца. При переходе клетки в возбужденное состояние, на мембране происходит изменение электрического потенциала: на смену отрицательному потенциалу покоя приходит положительный потенциал действия. Этот процесс сопряжен с переносом ионов через мембрану. Клеточная мембрана в спокойном состоянии поляризована таким образом: внутри клетки – минус, снаружи – плюс. При переходе клетки в возбужденное состояние происходит деполяризация мембраны: устанавливается внутри клетки – плюс, снаружи – минус. После того, как возбужденная клетка выполнила свою главную функцию - сократительную, она возвращается в спокойное состояние; восстанавливаются и начальные концентрации ионов по обе стороны мембраны. Происходит восстановительный процесс - реполяризация. Переходы клеток в возбужденное состояние и последующий их возврат в спокойное состояние носят массовый характер, и в различных участках миокарда это начинается, происходит и заканчивается не одновременно. Поэтому можно говорить о волнах деполяризации и реполяризации, распространяющихся по сердцу в целом и по отдельным его частям – предсердиям, желудочкам, перегородкам. 2. Электрический диполь. Токовый диполь. Интегральный электрический вектор сердца. Представлениям о сердце как органе, по которому распространяются волны деполяризации и реполяризации, соответствует модель, согласно которой сердце – это электрический токовый диполь, электрическое поле которого ощутимо за пределами сердца, и может регистрироваться с помощью системы электродов, помещенных на поверхности тела. Ниже рассматриваются две модели диполя, и обе – электрические. Электрический диполь – это система из двух равных по величине зарядов +q и – q, находящихся в непроводящей среде и разделенных промежутком L – плечом диполя (рис. 1). Дипольный момент электрического диполя – это вектор, модуль которого р = qL. Направление вектора электрического диполя: от отрицательного полюса (-) к положительному (+). Эта система зарядов, как целое, электрически нейтральна: +q – q = 0. 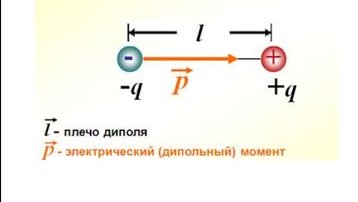 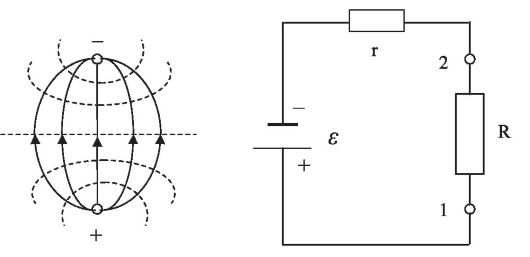 Рис.1.Электрический диполь. Рис.2. К понятию «токовый диполь». На рис. 2, справа, по замкнутой цепи протекает электрический ток силой I. Участок 1 – 2 с током I, имеющий протяженность L, можно рассматривать как токовый диполь: - точка 1 для него – положительный полюс, «исток»; - точка 2 – отрицательный полюс, «сток»; - участок 1-2, имеющий длину L, называется плечом токового диполя. Токовый диполь – это двухполюсная системав проводящей среде, с положительным полюсом – истоком и отрицательным – стоком тока. Дипольный момент токового диполя – это вектор, направленный от истока (+) к стоку (-) и численно равный произведению силы тока на плечо диполя: РТ = IL На рис. 2, слева, сплошные линии – это силовые линии электрического поля, создаваемого полюсами диполя в однородной проводящей среде; пунктирные линии – это линии, на каждой из которых электрический потенциал – константа (линии равного потенциала; эквипотенциальные линии). Электрический и токовый диполь – это электрические модели, призванные упростить понимание реальных процессов. Электрический диполь – модель, хорошо соответствующая строению молекул, некоторым видам их взаимодействия друг с другом, их поведению в постоянных и переменных внешних электрических полях. Электрический дипольный момент имеет в системе СИ единицу измерения 1 Кл·м, но это – очень большая величина, и для молекул применяется внесистемная единица – дебай: 1 Д = 3,33·10-30 Кл·м. Для электрокардиографии более подходящей оказалась модель токового диполя. Эта модель дает возможность рассматривать электрические процессы, происходящие при работе сердца, с учетом того, что большинство тканей организма хорошо проводит электрический ток. Процессы деполяризации и реполяризации клеток можно рассматривать как токи в проводящей среде. В токовом диполе на схеме рис. 2, протекание тока происходит за счет ЭДС источника тока, имеющегося в цепи. Электрические процессы в живых клетках обеспечиваются химической энергией молекул АТФ, синтезируемых в их митохондриях. Можно сказать, источники тока вживлены в мышечные волокна миокарда. Векторная сумма дипольных моментов токовых диполей всех клеток сердца – это вектор дипольного момента сердца – интегральный электрический вектор сердца (ИЭВС). На рис. 3 представлены некоторые характеристики его электрического поля. 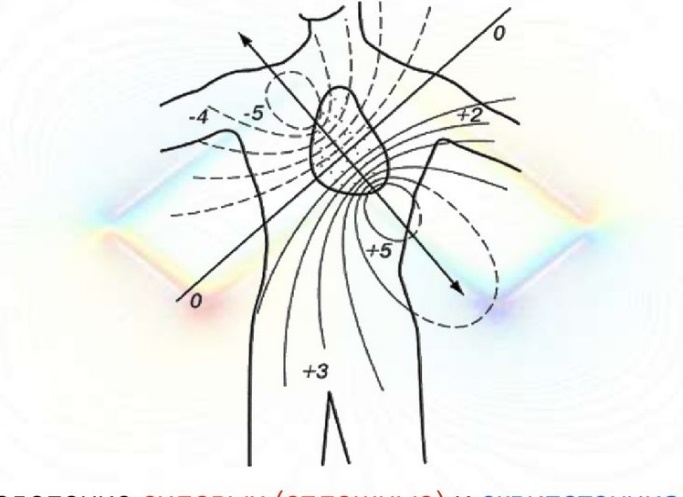 Рис. 3 Электрическое поле токового диполя сердца. (см. для сравнения рис.2, схема слева). Линия 0-0 – линия нулевого потенциала. ИЭВС лежит на перпендикуляре к линии 0-0. Правильное направление (из двух вариантов) определите сами. Кривые - эквипотенциальные линии с положительными и отрицательными значениями потенциала. В ходе сердечного сокращения ИЭВС меняется как по величине, так и по направлению в пространстве. Так что на рис. 3 представлена некоторая усредненная картина. Отведением в электрокардиографии называется система из двух электродов, установленных на поверхности тела пациента и подключенных к электрокардиографу. Регистрируемая в любом отведении разность потенциалов является проекцией ИЭВС на линию, соединяющую электроды этого отведения. Задачу воссоздания вектора ИЭВС по двум его проекциям вам предстоит решать графически в ходе выполнения данной работы. Опытный кардиолог имеет навыки оценки ИЭВС и его угла наклона, анализируя лишь его проекции – записи ЭКГ в отведениях, и не прибегая к графическим построениям. 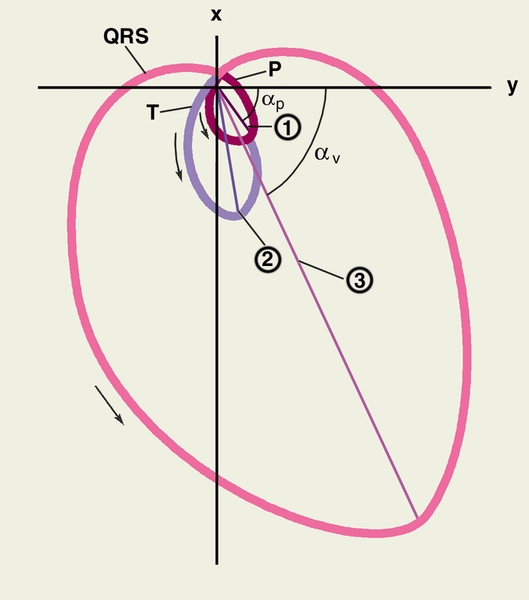 Но есть принципиальная возможность наблюдать этот вектор в ходе обследования в режиме реального времени. Задача о непрерывном воссоздании вектора ИЭВС по его меняющимся проекциям решается методом вектор-электрокардиографии (ВЭКГ). Но есть принципиальная возможность наблюдать этот вектор в ходе обследования в режиме реального времени. Задача о непрерывном воссоздании вектора ИЭВС по его меняющимся проекциям решается методом вектор-электрокардиографии (ВЭКГ). На мониторе вектор-кардиографа наблюдается замкнутая петлеобразная кривая, состоящая из трех петель. Ее описывает конец вектора ИЭВС за время цикла сердечного сокращения. Характер кривой представлен на рис. 4. Рис. 4. Вектор-электрокардиограмма. На рис 4 большую петлю описывает конец вектора ИЭВС в то время, когда обычный электрокардиограф записывает зубцы Q, R, S, соответствующие стадии сокращения желудочков. (см. схему на рис. 6). Петля 2 соответствует стадии реполяризации (зубец Т на обычной записи ЭКГ). Небольшая петля 1 соответствует зубцу Р. Вектор ИЭВС лежит на линии 3. Отклонения от нормы при работе сердца отслеживаются на ВЭКГ деформациями петель, их угловыми смещениями, нарушениями симметрии. | |||||||||||||||||||||||||||||||||||||||||
