Петровых и др.Ч.4.-ЭЛЕКТР. И ЭЛ.-уч.-метод.пос.-от02фев22. Учебнометодическое пособие для студентов всех специальностей, изучающих дисциплины Электротехника и электроника
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
Мгновенное значение электрического тока – значение электрического тока в рассматриваемый момент времени. Периодический электрический ток – электрический ток, мгновенные значения которого повторяются через равные промежутки времени. Переменный электрический ток – электрический ток, изменяющийся с течением времени по величине и направлению. Синусоидальный электрический ток – периодический ток, изменяющийся во времени по синусоидальному закону. Период электрического тока (Т) – наименьший интервал времени, в течение которого мгновенное значение тока, изменяясь по значению и направлению, принимает свое первоначальное, для данного отсчета, значение. Для синусоидального тока период соответствует 2πрадиан (или 360°). Частота электрического тока (f)– величина, обратная периоду электрического тока, вычисляется по формуле, Гц 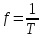 . (3) . (3)Угловая частота синусоидального электрического тока (ω) – скорость изменения фазы тока, c-1 ω = 2πƒ. (4) Фаза синусоидального электрического тока – аргумент синусоидального тока. Например, в формуле i = Iт∙sin(ωt+ ψi) фазой тока является выражение ωt+ ψi. Начальная фаза синусоидального электрического тока – значение фазы синусоидального тока в начальный момент времени. В приведенном выше примере начальной фазой является угол ψi. По модулю и знаку начальной фазы определяют, какая из функций является опережающей, а это, в свою очередь, имеет существенное значение при исследовании электрических цепей. Знакначальной фазы можно определить по знаку мгновенного значения функции при t= 0, а модульеё – есть длина отрезка на оси абсцисс в масштабе аргумента функций, расположенного между началом координат и ближайшей к началу координат точкой, в которой функция, возрастая, пересекает ось абсцисс. Пример. На рис. 3 приведены две функции тока: i1=Iт1 sin(ωt + ψi1); i2=Iт2 sin(ωt – ψi2), 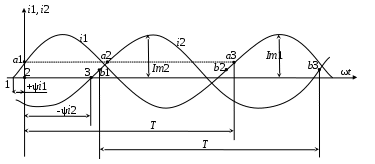 мгновенные значения которых изменяются с периодом Т. Рис. 3. К определению модуля и знака начальной фазы и периода тока При t = 0, i1 > 0, i2 < 0, следовательно, начальные фазы токов «+» ψi1 и «–» ψi2. Модули начальных фаз: для тока i1 – отрезок 1 – 2; для тока i2 – отрезок 2 – 3. Период функций тока: Т соответствует отрезку а1 – а3, (но не а1 – а2, хотя и ia1 = ia2, так как в интервале а1 – а2 функция не изменяла своего знака). Действующий периодический электрический ток (I)– среднее квадратичное значение электрического тока за период, т. е. значение постоянного тока, выделяющего за период Т на резисторе такое же количество тепла, что и периодический ток за тот же интервал времени. В общем виде 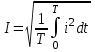 . (5) . (5)Для синусоидального тока с начальной фазой ψi 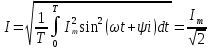 , (6) , (6)где Iт – максимальное (амплитудное) значение синусоидального тока. Для синусоидальных ЭДС и напряжений действующие значения можно записать 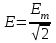 ; ; 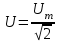 . (7) . (7)Шкалы амперметров и вольтметров электромеханических систем градуируют в действующих значениях тока и напряжения. Используя выражение (7), можно определить максимальные токи, ЭДС и напряжения исследуемых электрических цепей. Угол сдвига фаз между напряжением и током (φ) – алгебраи-ческая величина, определяемая путем вычитания начальной фазы тока из начальной фазы напряжения: φ = ψu – ψi. (8) Электрическая цепь – совокупность элементов, образующих путь для электрического тока. Элемент электрической цепи – отдельное устройство, входящее в состав электрической цепи и выполняющее в ней отдельную функцию. Примеры: Резистор – элемент, обладающий активным сопротивлением. Конденсатор – элемент, обладающий реактивным емкостным сопротивлением. Катушка индуктивности – элемент, обладающий активным и реактивным индуктивным сопротивлениями. Участок электрической цепи – часть электрической цепи, содержащая определенную совокупность ее элементов. Ветвь электрической цепи – участок электрической цепи, по которому протекает один и тот же ток. Узел электрической цепи – место соединения трех и более ветвей электрической цепи. Синусоидальные функции можно изобразить на плоскости временными и векторными диаграммами. Временные диаграммы наглядно показывают процессы изменения во времени мгновенных значений физических величин и могут быть построены в одной системе координат для функций с различными частотами, но требуют выполнения значительного объема графических работ. Пример построения временных диаграмм синусоидального тока приведен на рис. 3. Векторные диаграммы просты в построении, но в то же время они не дают наглядного представления о процессах изменения физических величин и могут быть построены в одной системе координат только для функций, имеющих одинаковую частоту. Векторные диаграммы строят на комплексной плоскости. В электротехнике широко используют диаграммы – метод комплексных чисел (символический метод). Комплексная плоскость – плоскость, проходящая через две взаимно перпендикулярные оси – вещественную и мнимую. Реальные синусоидальные функции можно заменить соответствующими символами, в качестве которых используются комплексные числа. Расчет производится в комплексной форме записи. Результаты расчета переводятся обратно в синусоидальную функцию времени. Например, функцию 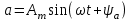 можно представить вектором Am,вращающимся с угловой частотой ω = const от точки, формирующей начальную фазу ψа (рис. 4). можно представить вектором Am,вращающимся с угловой частотой ω = const от точки, формирующей начальную фазу ψа (рис. 4).В комплексной форме записи эта функция будет выглядеть так: 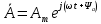 , ,при t = 0, ωt = 0 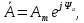 –показательная форма записи комплексного числа. –показательная форма записи комплексного числа.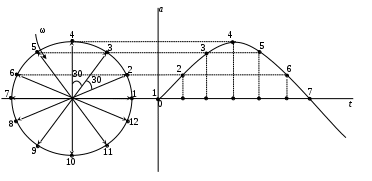 Рис. 4. Изображение синусоидальной величины а в виде вектора А Также комплексное число можно представлять в алгебраической форме записи: 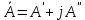 и тригонометрической форме записи: 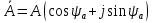 , ,где j – мнимая единица, 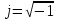 ; ; 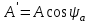 – вещественная (действительная) часть комплексного числа; – вещественная (действительная) часть комплексного числа;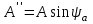 – мнимая часть; – мнимая часть;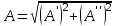 – модуль комплексного числа; – модуль комплексного числа;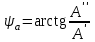 – аргумент комплексного числа; – аргумент комплексного числа;е – основание натурального логарифма, 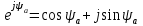 . . Любое комплексное число можно изобразить вектором на комплексной плоскости (рис. 5). Сопряженное комплексное число – это комплексное число с противоположным знаком при мнимой части. Если комплексное число имеет вид 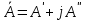 , сопряженное комплексное число , сопряженное комплексное число 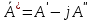 (рис. 6). (рис. 6).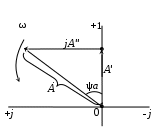 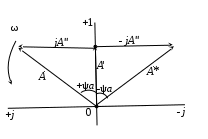
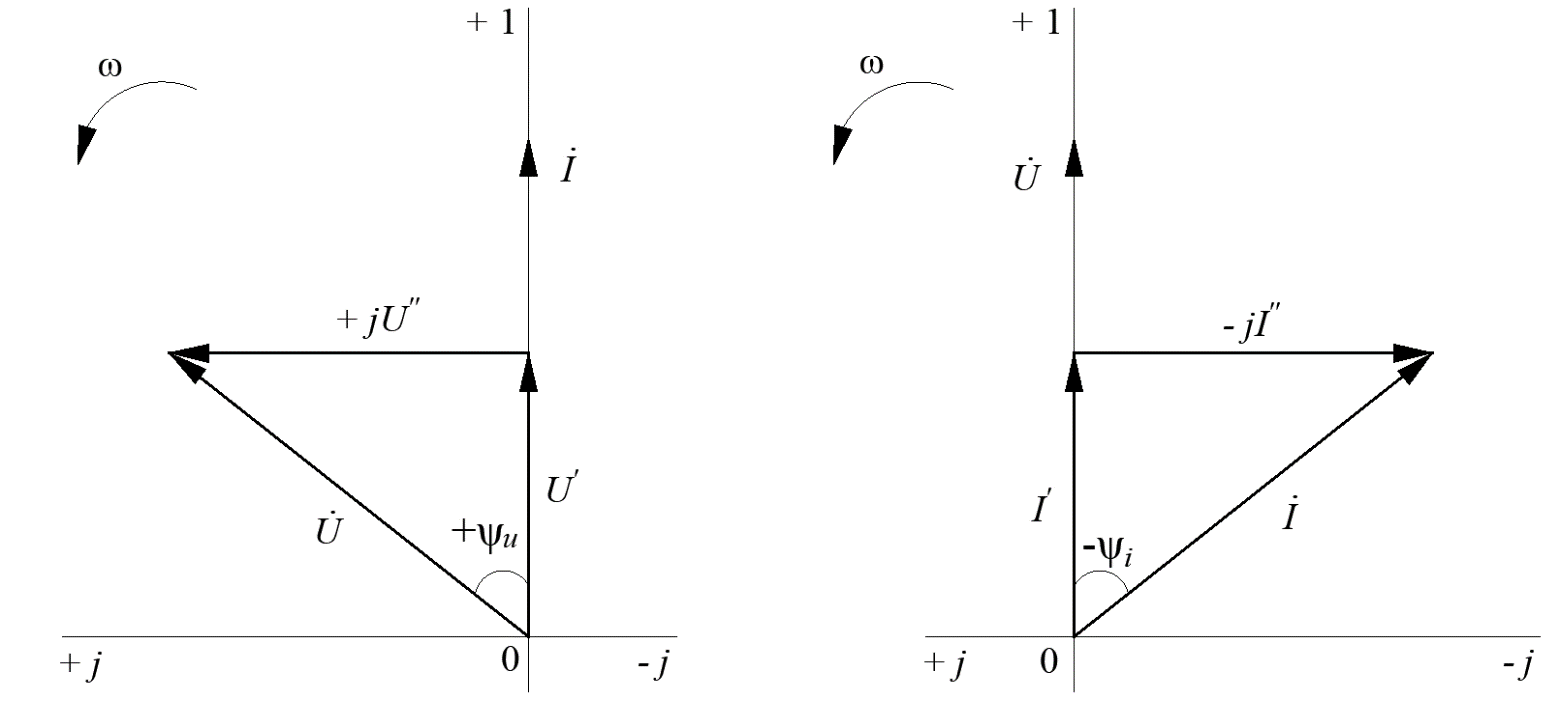 Рис. 7. Изображение тока и напряжения на комплексной плоскости Пример построения векторов комплексов действующих напряжения и тока однофазной цепи, заданных уравнениями: 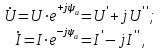 (9) (9)где U' и U'', I' и I'' – соответственно вещественные и мнимые части комплексов действующих напряжения и тока (рис. 7). Лабораторная работа 4 ИССЛЕДОВАНИЕ ТРЁХФАЗНЫХ ЦЕПЕЙ ПРИ СОЕДИНЕНИИ ФАЗ ПОТРЕБИТЕЛЯ ТРЕУГОЛЬНИКОМ Цель работы Экспериментально установить влияние характера, несимметрии нагрузки и неполнофазного режима работы, на токи и напряжения исследуемой цепи. Определить соотношения между фазными, линейными токами и напряжениями при различных режимах работы потребителя. Общие сведения Соединить фазы потребителя треугольником – это последовательно соединить все его фазы, образовав треугольник a-b-с, к началам фаз потребителя а, b, с подается напряжение от источника питания (рис. 4.1). 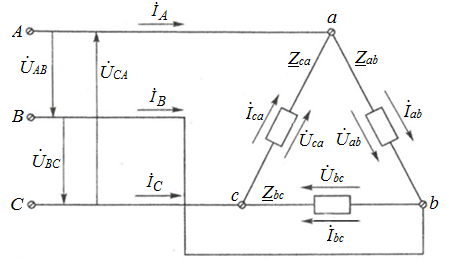 Рис. 4.1. Схема соединения фаз потребителя треугольником На рис. 4.1: 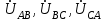 – линейное напряжение источника (UЛ); – линейное напряжение источника (UЛ);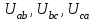 – фазные напряжения нагрузки (UФ); – фазные напряжения нагрузки (UФ);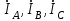 – линейные токи (IЛ); – линейные токи (IЛ);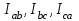 – фазные токи нагрузки (IФ); – фазные токи нагрузки (IФ);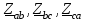 – полные комплексные сопротивления фаз нагрузки. – полные комплексные сопротивления фаз нагрузки.Если пренебречь потерями напряжения в соединительных проводах, то фазные напряжения нагрузки равны, соответствующимлинейнымнапряжениямсети, т. е. 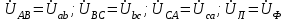 . (4.1) . (4.1)Расчеты в 3-фазной электрической цепи при соединении нагрузки треугольником осуществляются по следующим формулам: напряжения нагрузки на комплексной плоскости 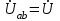 ; ;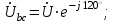 (4.2) (4.2)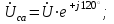 комплексы фазных действующих токов потребителя вычисляются согласно закону Ома по формулам: 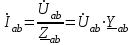 ; ;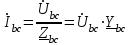 ; (4.3) ; (4.3)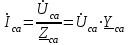 , ,где 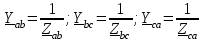 –комплексы проводимостей фазных нагрузок; –комплексы проводимостей фазных нагрузок;линейные токи сети вычисляются на основании первого закона Кирхгофа для узлов а, b и с цепи потребителя 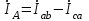 ; ;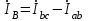 ; (4.4) ; (4.4)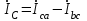 ; ;комплексная полная мощность для каждой фазы потребителя 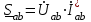 ; ;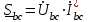 ; (4.5) ; (4.5)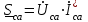 . .полная мощность 3-фазной цепи 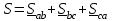 . .При симметричной нагрузке в фазах потребителя 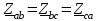 ; фазные токи ; фазные токи 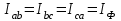 ; линейные токи ; линейные токи 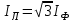 ; полная мощность трехфазной цепи ; полная мощность трехфазной цепи 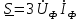 . .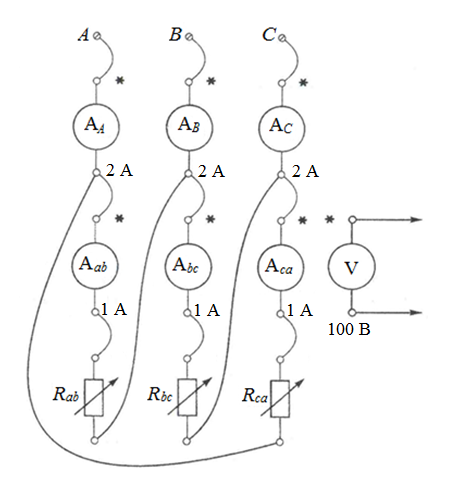 Рис. 4.2. Монтажная схема для соединения фаз нагрузки треугольником Программа исследований Последовательность выполнения работы: Собрать монтажную схему опыта, приведенную на рис. 4.2. Провести эксперименты в соответствии с перечнем (табл. 4.1). Установить регулировочными устройствами резисторов Rab, Rbc, Rca заданные преподавателем значения сопротивлений и измерить напряжения потребителя, линейные и фазные токи потребителя для режимов, приведенных в табл. 4.1. Записать в табл. 4.1 измеренные значения токов и напряжений исследуемой цепи. Таблица 4.1 |
