Учебнометодическое пособие к лабораторнопрактическим занятиям по дисциплине Введение в информационные технологии для студентов направления подготовки 44. 03. 04 Профессиональное обучение всех форм обучения
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
Задание для самостоятельного выполненияПереведите: 14110 → X2 14110 → X8 14110 → X16 Для перевода правильных дробей из десятичной системы счисления в произвольную используется метод последовательного умножения на основание системы счисления дробных цифр числа до тех пор, пока не получим в дробной части всех нулей или не достигнем заданной точности (если число не переводится точно). Пример. Перевести из десятичной системы счисления в двоичную число 0,325. 0,375 x 2 ––––– 0,750 Выделяем целую часть: 0 0,750 x 2 ––––– 1,500 Выделяем целую часть: 1 0,500 x 2 ––––– 1,000 В дробной части получили все нули, т.е. число перевелось в двоичную систему счисления точно: 0,0112. Двоичная арифметика 1. Таблица сложения 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 2. Таблица вычитания 0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 3. Таблица умножения 0 ∙ 0 = 0 1 ∙ 0 = 0 1 ∙ 1 = 1 Пример. Сложить два числа в двоичной системе счисления. 1 1 0 1 1 + 1 0 1 1 0 1 ––––––––––- 1 0 0 1 0 0 0 Количество информации, которое вмещает один символ N-элементного алфавита, равно i = log2N. Это известная формула Р. Хартли. В 32-значном алфавите каждый символ несет i = log232 = 5 (бит) информации. Пример 1. Вычислить количество информации в слове «Информатика» при условии, что для кодирования используется 32-значный алфавит. Решение. Вычислим количество информации, соответствующее 1 символу при использовании 32-значного алфавита: 32 = 2х, х = 5 бит. Слово "Информатика" состоит из 11 символов, получаем 11* 5 = 55 (бит). Пример 2. Растровый графический файл содержит черно-белое изображение с 2 градациями цвета (черный и белый) размером 800 х 600 точек. Определите необходимый для кодирования цвета точек (без учета служебной информации о формате, авторстве, способах сжатия и пр.) размер этого файла на диске в байтах. Решение. Поскольку сказано, что изображение двуцветное, следовательно, для указания цвета одной точки достаточно двух значении, кодирующих белый или черный цвет. Два значения могут быть закодированы одним битом. Объем графического файла рассчитывается по формуле V=i*k, где i - глубина цвета, а k - количество точек. Тогда объем графического файла равен 800 * 600 * 1 бит = 480 000 6ит, учитывая, что 8 бит = 1 байт получаем 480 000 / 8 = 60 000 байтов. В реальности в графических документах кроме описания цвета точек присутствует еще и служебно-дополнительная информация (о формате записи, авторских правах, способах сжатия и пр.). Использование различных кодировок В кодировке ASCII на каждый символ отводится 1 байт = 8 бит. В кодировке Unicode на каждый символ отводится 2 байта = 16 бит. Пример 1. При кодировании с помощью Unicode найти информационный объем фразы «Ученье – свет, а неученье – тьма!». Решение. Подсчитаем число символов в заданной фразе, учитывая буквы, пробелы и знаки препинания (тире, запятую, восклицательный знак). Всего символов – 33. Вычислим объем фразы: 33 (символа) * 2 (байта) = 66 байт = 528 бит. Пример 2. Сообщение содержит 4096 символов. Объем сообщения при использовании равномерного кода составил 1/512 Мбайт. Найти мощность алфавита, с помощью которого записано данное сообщение. Решение. Мощность алфавита – количество символов в алфавите. Переведем информационный объем сообщения в биты. 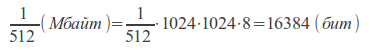 Для кодирования одного символа отводится 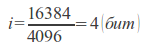 Тогда мощность алфавита по формуле Р. Хартли равна N = 2i = 24 = 16. Пример 3. Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с для передачи 100 страниц текста в 30 строк по 60 символов каждая в кодировке ASCII. Решение. В кодировке ASCII каждый символ занимает 8 бит или 1 байт. Тогда объем текста равен 100 ∙ 30 ∙ 60 ∙ 8 = 1 440 000 битов. Для его передачи по модему потребуется Перевод количества информации между различными единицами измерения 1 бит – минимальная неделимая единица информации. 8 бит составляют 1 байт, таким образом 1 байт = 8 бит 1 Кбайт (килобайт) = 1024 = 210 байт 1 Мбайт (мегабайт) = 1024 = 210 Кбайт = 220 байт 1 Гбайт (гигабайт) = 1024 = 210 Мбайт = 220 Кбайт = 230 байт 1 Пбайт (петабайт) = 1024 = 210 Гбайт = 220 Мбайт = 230 Кбайт = 240 байт Пример 1. Перевести 376832 бит в Кбайт. Решение. 376832 бит = 376832 / 8 = 47104 байт = 47104 / 1024 = 46 Кбайт Пример 2. Перевести 37 Кбайт 515 Байт 3 бит в бит. Решение. 37 Кбайт 515 байт 3 бит = 37 ∙ 1024 + 515 байт 3 бит = 38403 байт 3 бит = 38403 ∙ 8 +3 = 307227 бит. С дополнительным теоретическим материалом можно ознакомиться в литературе [2, 7]. Варианты задания |
