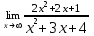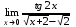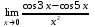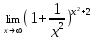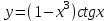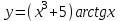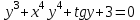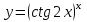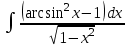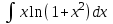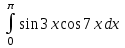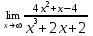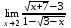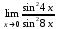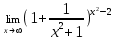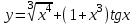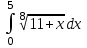ВМ. ВМ 11.03.02 1 курс 1 семестр МУиКЗ. Учебнометодическое пособие по курсу высшая математика часть 1 для студентов Центра заочного образования по программе
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
Раздел 5. Определители. Матрицы. Системы линейных уравнений Рассмотрим определители второго и третьего порядка. Определителем второго порядка называется число 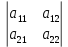 = =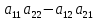 . Например, определитель . Например, определитель 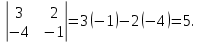 Определитель третьего порядка имеет вид: 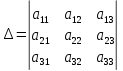 . Возьмем произвольный элемент определителя и вычеркнем строку и столбец, в котором он стоит. Оставшиеся элементы образуют определитель второго порядка, который называется минором по отношению к вычеркнутому элементу. Например, для элемента . Возьмем произвольный элемент определителя и вычеркнем строку и столбец, в котором он стоит. Оставшиеся элементы образуют определитель второго порядка, который называется минором по отношению к вычеркнутому элементу. Например, для элемента 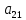 минором является определитель минором является определитель 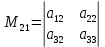 . Тогда, для произвольного элемента . Тогда, для произвольного элемента 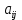 алгебраическим дополнением является алгебраическим дополнением является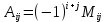 . .В частности для элемента 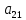 алгебраическое дополнение равно алгебраическое дополнение равно 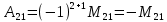 . Тогда определитель третьего (впрочем, как и любого другого ) порядка можно разложить по любой строке (столбцу) следующим образом. . Тогда определитель третьего (впрочем, как и любого другого ) порядка можно разложить по любой строке (столбцу) следующим образом.Возьмем, например, первую строку. Тогда определитель 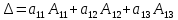 . .Например, 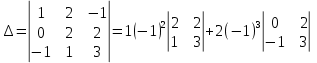 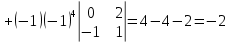 . .Рассмотрим на примере применение определителей для решения систем линейных уравнений. Задача 5.1. Решить систему линейных уравнений по методу Крамера. 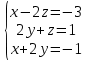 . .Составим определитель из коэффициентов системы и вычислим его, разложив по первой строке. Такой определитель называется главным определителем системы. 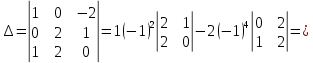 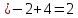 . .Далее составим так называемые вспомогательные определители. Их три. Определитель 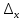 получается из главного определителя получается из главного определителя 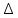 путем замены первого столбца, соответствующего коэффициентам при путем замены первого столбца, соответствующего коэффициентам при  , столбцом свободных членов. Запишем разложение этого определителя по второму столбцу. , столбцом свободных членов. Запишем разложение этого определителя по второму столбцу.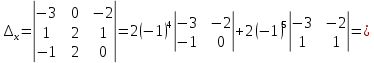 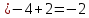 . .Аналогично составим и вычислим два других вспомогательных определителя 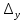 и и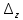 . .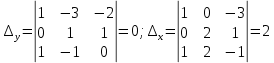 . .Применяя метод Крамера , найдем решения системы:  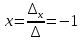 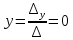 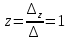 Ответ: 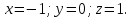 Рассмотрим матричный метод решений системы линейных уравнений. Прямоугольная таблица чисел, состоящая из 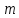 строк и строк и 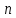 столбцов называется числовой матрицей столбцов называется числовой матрицей 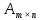 ( далее – просто «матица»). Например, матрица ( далее – просто «матица»). Например, матрица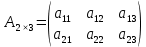 Заметим, что в отличие от определителя, в котором число строк и столбцы совпадает, матрица может содержать любое, не обязательно совпадающее, число строк и столбцов. Рассмотрим действия (или операции) над матрицами: 1. Умножение матрицы на число. Любую матрицу можно умножить на произвольное действительное число. При этом каждый элемент матрицы умножается на это число. 2. Сумма матриц это матрица, каждый элемент которой является суммой элементов слагаемых, стоящий на одноименных местах. Сумма матриц определена только для матриц одинаковой размерности. 3. Произведение матриц. Произведением двух матриц  и и 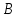 называется матрица называется матрица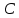 , у которой элемент , у которой элемент 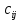 равен сумме произведений каждого элемента равен сумме произведений каждого элемента  –ый строки матрицы –ый строки матрицы  на соответствующие элементы на соответствующие элементы 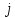 –го столбца матрицы A –го столбца матрицы A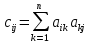 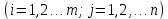 . . Замечание. Умножение двух прямоугольных матриц возможно только в том случае, когда число столбцов левой матрицы равно числу строк правой матрицы, т.е. 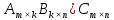 . .Задача 5.2. Найти произведение матриц 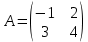 и и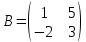 . .Решение. Пусть 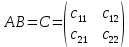 . .Для вычисления 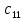 берем первую строку из первого определителя и первый столбец из второго определителя: берем первую строку из первого определителя и первый столбец из второго определителя: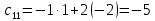 . .Для вычисления 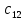 берем первую строку из первого определителя и второй столбец из второго определителя: берем первую строку из первого определителя и второй столбец из второго определителя: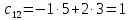 . . Аналогично: 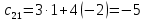 , , 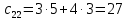 . . Ответ: 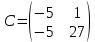 Рассмотрим теперь квадратные матрицы, у которых число столбцов и число строк совпадает на примере матриц третьего порядка. Приведем следующие определения: Единичная матрица третьего порядка имеет вид: 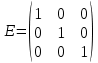 . Здесь просматривается некоторая аналогия с единицей в множестве действительных чисел, то есть для любой матрицы . Здесь просматривается некоторая аналогия с единицей в множестве действительных чисел, то есть для любой матрицы  выполняется соотношение: выполняется соотношение: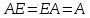 . .Квадратная матрица, имеющая определитель  , отличный от нуля , отличный от нуля 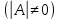 , называется невырожденной матрицей. Любая невырожденная матрица имеет обратную матрицу , называется невырожденной матрицей. Любая невырожденная матрица имеет обратную матрицу 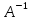 : :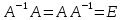 . .Метод определения обратной матрицы приведен в следующем примере: Задача 5.3. Найти обратную матрицу для матрицы 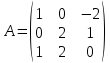 . .Решение. Сначала проверяем матрицу на новорожденность и вычисляем  . Определитель этой матрицы вычислен в задаче 5.2: |A|=2 . Определитель этой матрицы вычислен в задаче 5.2: |A|=2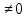 . Отсюда следует, что матрица невырожденная и, поэтому, имеет обратную матрицу. Нахождение обратной матрицы состоит из трех шагов: . Отсюда следует, что матрица невырожденная и, поэтому, имеет обратную матрицу. Нахождение обратной матрицы состоит из трех шагов:Шаг 1: Построение матрицы 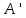 , состоящей из алгебраических дополнение элементов матрицы , состоящей из алгебраических дополнение элементов матрицы  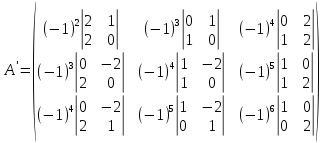 = =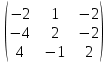 . .В этом случае мы каждый элемент исходной матрицы заменяем на его алгебраическое дополнение. Шаг 2. Производим с матрицей 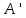 операцию транспонирования, то есть операцию преобразования всех строк матрицы в одноименные столбцы: операцию транспонирования, то есть операцию преобразования всех строк матрицы в одноименные столбцы: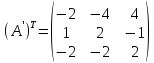 . .Шаг 3. Умножаем полученную матрицу на 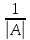 , в нашем случае на , в нашем случае на 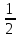 : :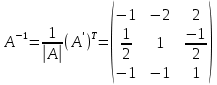 . .В случае нахождения обратной матрицы рекомендуется сделать проверку и убедиться, что полученная матрица является обратной к заданной. Система из трех линейных уравнений с тремя неизвестными может быть записана матричным способом. Введем следующие матрицы: 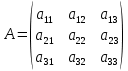 ; ; 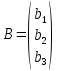 ; ; 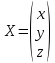 , ,где 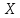 - матрица системы, B – матрица-столбец свободных членов и - матрица системы, B – матрица-столбец свободных членов и 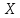 - матрица неизвестных. Тогда систему можно представит в виде: - матрица неизвестных. Тогда систему можно представит в виде: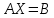 . .Умножая правую и левую части последнего соотношения на 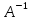 , слева, получим: , слева, получим: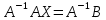 , , 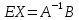 , , 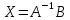 . . Задача 5.4. Найти решение системы линейных уравнений, заданной в задаче 5.1, матричным способом. Решение. Для матрицы системы в задаче 5.1 найдена обратная матрица 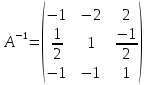 . Учитывая, что матрица свободных членов данной системы . Учитывая, что матрица свободных членов данной системы 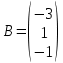 , получим решение системы в виде: , получим решение системы в виде: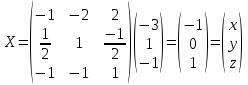 . .Ответ: 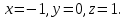 Контрольная работа №1 1. Вычислить указанные пределы, не пользуясь правилом Лопиталя. 2. Вычислить производные указанных функций. 3. Вычислить неопределенные интегралы. 4. Вычислить определенный интеграл 5. Решить систему линейных уравнений по правилу Крамера и матричным методом. Вариант 00
Вариант 01
|