ВМ. ВМ 11.03.02 1 курс 1 семестр МУиКЗ. Учебнометодическое пособие по курсу высшая математика часть 1 для студентов Центра заочного образования по программе
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
Раздел 2. Производная функции и ее приложения Пусть функция  определена в некоторой точке определена в некоторой точке  и в окрестности этой точки, а и в окрестности этой точки, а 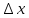 – приращение аргумента, такое, что – приращение аргумента, такое, что 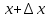 принадлежит указанной окрестности. Тогда принадлежит указанной окрестности. Тогда 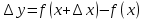 называется приращением данной функции. Если существует называется приращением данной функции. Если существует 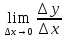 , ,то этот предел называется производной функции 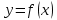 в точке в точке  и обозначается и обозначается 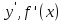 или или 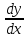 , а функция называется дифференцируемой в точке , а функция называется дифференцируемой в точке  . .Функция 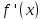 , определенная во всех точках, в которых существует указанный предел, называется производной функции , определенная во всех точках, в которых существует указанный предел, называется производной функции 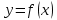 . .Рассмотрим технику вычисления производных или, другими словами, технику дифференцирования. Таблица производных элементарных функций: 1. 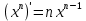 9. 9. 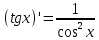 1* 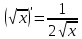 10. 10. 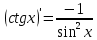 1**. 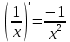 11. 11. 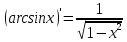 2. 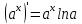 12. 12. 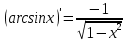 2*. 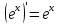 13. 13. 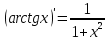 3. 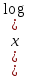 14. 14. 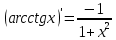 3*. 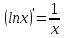 15. 15. 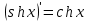 4. 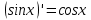 16. 16. 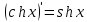 8. 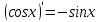 Правила дифференцирования. Пусть 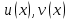 – произвольные функции, – произвольные функции, 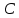 – константа (постоянная величина). Тогда: – константа (постоянная величина). Тогда:1. 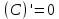 2. 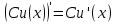 3. 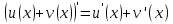 4. 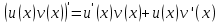 5. 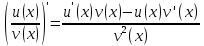 Задача 2.1. Вычислить производную функции: 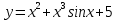 . .Решение. 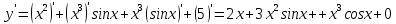 . .Ответ: 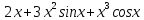 . .При вычислении производных необходимо обратить особое внимание на дифференцирование сложной функции. Пусть даны две функции  и и 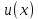 . Сложной функцией называется функция . Сложной функцией называется функция 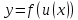 Производная сложной функции вычисляется по формуле: Производная сложной функции вычисляется по формуле: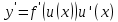 . .Задача 2.2. Вычислить производную сложной функции: 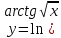 ). ).Решение. При вычислении производной сложной функции, прежде всего надо понять порядок применения последовательности функций к аргументу  . Так, в данной функции сначала из аргумента извлекается квадратный корень, далее от полученного значения вычисляется арктангенс, и, наконец, вычисляется натуральный логарифм. Вычисление производной происходит в обратном порядке, то есть, начиная с логарифма: . Так, в данной функции сначала из аргумента извлекается квадратный корень, далее от полученного значения вычисляется арктангенс, и, наконец, вычисляется натуральный логарифм. Вычисление производной происходит в обратном порядке, то есть, начиная с логарифма: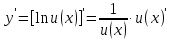 , где , где 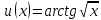 . .Таким образом, мы получаем следующую цепочку равенств: 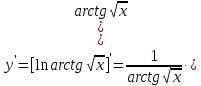 = =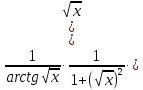 = == 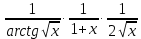 . .Задача 2.3. (первый способ). Вычислить производную функции 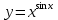 . .Решение. Преобразуем данную функцию к виду, удобному для дифференцирования, использовав основное логарифмическое тождество 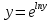 . .Получим: 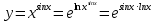 . .Далее, применив алгоритм дифференцирования сложной функции, а также формулу дифференцирования произведения, получим: 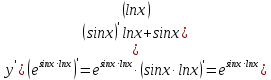 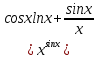 ). ).Рассмотрим дифференцирование функции, заданной неявно. Если функция представлена в виде 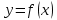 , то говорят, что функция представлена в явном виде. Если же задана функция , то говорят, что функция представлена в явном виде. Если же задана функция 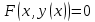 , то есть некая функция, связывающая между собой , то есть некая функция, связывающая между собой  и и 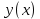 , то такое задание функции называется неявным. , то такое задание функции называется неявным.Задача 2.4. Найти производную функции, заданной неявно: 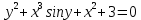 Решение. Перепишем данное соотношение в несколько ином виде, подчеркнув, что  – это независимый аргумент, а – это независимый аргумент, а 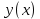 – это функция, производную которой нам требуется найти. – это функция, производную которой нам требуется найти.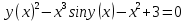 . . Вычислим производную правой и левой частей: 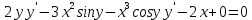 . .Сконцентрируем слагаемые, содержащие искомую производную, в левой части и вынесем 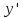 за скобку, а остальные слагаемые перенесем в правую часть, изменив знак на противоположный: за скобку, а остальные слагаемые перенесем в правую часть, изменив знак на противоположный: . .Окончательно получим: 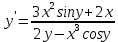 . .Ответ: 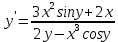 . .Задача 2.5. (второй способ). Вычислить производную функции 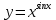 . .Решение: Прологарифмируем правую и левую часть явно заданной функции и перейдем к неявному ее заданию: 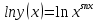 или или 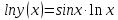 . .Вычисляя производную функции, заданной неявно, получим: 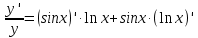 или или 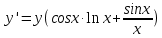 . Учитывая, что из условия задачи нам известно явное выражение для функции . Учитывая, что из условия задачи нам известно явное выражение для функции 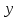 , получим: , получим: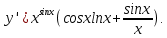 Раздел 3. Неопределенный интеграл функции одной переменной. Поставим задачу восстановления вида функции по ее производной, то есть, так называемой, первообразной функции. Функция 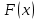 называетсяпервобразной для функции называетсяпервобразной для функции  на некотором промежутке, если для всех на некотором промежутке, если для всех  из этого промежутка из этого промежутка 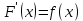 . .Например, если производная функции равна 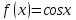 , то первообразной функцией является, например, функция , то первообразной функцией является, например, функция 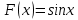 . Можно показать, что одна первообразная от другой отличается на константу. . Можно показать, что одна первообразная от другой отличается на константу.Неопределённым интегралом функции  называется совокупность всех ее первообразных и записывается как называется совокупность всех ее первообразных и записывается как 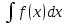 .Таким образом, .Таким образом, 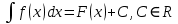 . Например, . Например, 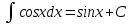 . .Таблица интегралов элементарных функций. 1. 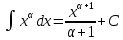 8. 8. 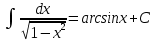 2. 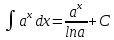 9. 9. 2*. 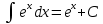 10. 10.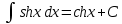 3. 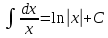 11. 11.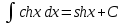 4.  12. 12.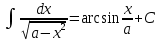 5. 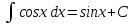 13. 13. 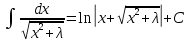 6. 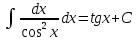 14. 14.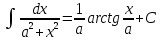 7. 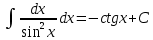 15. 15.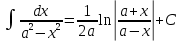 Свойства неопределенных интегралов. Пусть  – произвольная константа, – произвольная константа,  - функции. - функции.1. 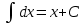 ; ;2. 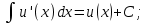 3. 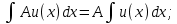 4. 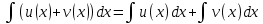 . .Заметим, что общих формул для вычисления интеграла от произведения (частного) не существует. Это не значит, что такие интегралы невозможно вычислить, просто для вычисления таких интегралов нет общих формул. Рассмотрим два основных метода вычисления неопределенных интегралов: Метод замены переменной и метод интегрирования по частям. Начнем с метода замены переменной в неопределенном интеграле. Задача 3.1. Вычислить неопределенный интеграл: 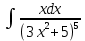 . .Решение. Используем для вычисления этого интеграла метод замены переменной, введя новую переменную 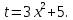 .В этом случае .В этом случае 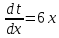 , откуда , откуда 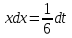 . Делая замену переменной в неопределенном интеграле и используя таблицу неопределенных интегралов, получим: . Делая замену переменной в неопределенном интеграле и используя таблицу неопределенных интегралов, получим: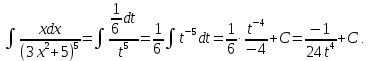 . .Возвращаясь к старой переменной, получим ответ:  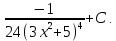 Задача 3.2. Вычислить неопределенный интеграл: 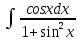 . .Решение. Введем новую переменную 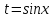 . В этом случае . В этом случае 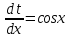 , откуда , откуда 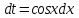 . Делая замену переменной в неопределенном интеграле, получим: . Делая замену переменной в неопределенном интеграле, получим: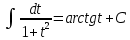 . .Возвращаясь к старой переменной, получим ответ:  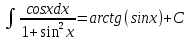 . .Задача 3.3. Вычислить неопределенный интеграл: 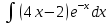 . .Решение. Используем формулу интегрирования по частям в виде: 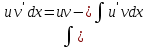 . .Замечание: В некоторых случаях формула интегрирования по частям записывается в виде: 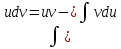 . .Введем обозначения и сделаем предварительные вычисления: 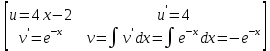 . .Подставляя все введенные и полученные функции в формулу интегрирования по частям, получим: 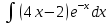 =-(4 =-(4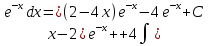 . .Раздел 4. Определённый интеграл функции одной переменной. Геометрические приложения. Несобственные интегралы Пусть на отрезке 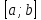 задана некоторая непрерывная функция задана некоторая непрерывная функция  . Криволинейная трапеция – это плоская фигура, ограниченная отрезком . Криволинейная трапеция – это плоская фигура, ограниченная отрезком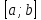 на оси на оси 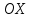 , прямыми , прямыми 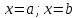 и графиком функции и графиком функции  . Площадь криволинейной трапеции записывается как . Площадь криволинейной трапеции записывается как 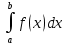 и называется определенным интегралом. и называется определенным интегралом.Основной формулой, используемой при вычислении определенного интеграла, является формула Ньютона – Лейбница, устанавливающая связь между определенным и неопределенным интегралами. Пусть 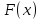 есть первообразная функция для функции есть первообразная функция для функции  . Тогда: . Тогда: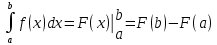 . .Задача 4.1. Вычислить определенный интеграл: 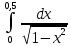 . .Решение. 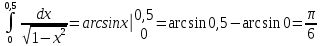 . .Ответ: 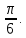 Задача 4.2. Вычислить определенный интеграл 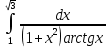 . .Решение. Сделаем замену 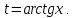 Тогда Тогда 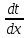 = =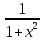 , а значит , а значит 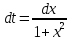 . При этом надо учитывать возможное изменение пределов интегрирования при замене переменной. В нашем случае нижний предел интегрирования . При этом надо учитывать возможное изменение пределов интегрирования при замене переменной. В нашем случае нижний предел интегрирования 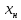 =1 переходит в =1 переходит в 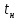 = =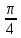 , верхний предел , верхний предел 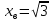 переходит в переходит в 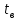 = =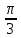 , а интеграл в результате замены переменной интеграл принимает вид: , а интеграл в результате замены переменной интеграл принимает вид: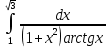 = =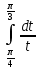 = =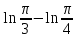 =ln =ln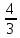 . .Рассмотрим использование метода интегрирования по частям в определенном интеграле, применив формулу: 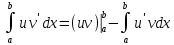 . .Задача 4. 3. Вычислить интеграл: 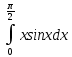 . .Решение. 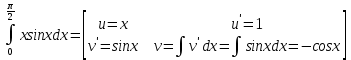 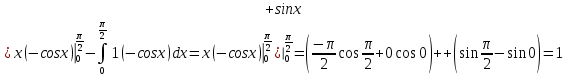 Ответ: 1. |
