Методология и методы психолого-педагогических исследований. Учебное пособие адресовано студентам педагогических учебных заведений, преподавателям кафедр педагогики и психологии, школьным учителям и психологам, аспирантам и соискателям, ведущим самостоятельную исследовательскую работу в сфере образования.
 Скачать 241.88 Kb. Скачать 241.88 Kb.
|
Г лава 7. Методы сводки и обработки результатов исследований§ 1. Количественная обработка материаловСтатистические методы исследовательской работы применяются на этапах планирования, сбора материалов, сводки и обработки материалов исследования и при представлении его результатов. Не следует преувеличивать значение применения статистических методов. Статистика не раскрывает педагогической сущности явлений. Этими средствами можно лишь констатировать статистически достоверные различия между двумя исследуемыми явлениями, но объяснение сущности причинно-следственных отношений этих различий должно осуществляться методами теоретического анализа. Статистика не требуется при углубленном изучении отдельного, единичного явления, но статистика необходима при рассмотрении совокупности явлений, состоящих из множества отдельных элементов. Отдельные явления, входящие в совокупность, называются элементами совокупности, обычно обозначаются xi и yi. Если обозначить частоту отдельных элементов fi, то их сумма (åfi) называется объемом совокупности и обозначается буквой N. Для количественной характеристики совокупностей используют главным образом средние показатели такие, как: среднее арифметическое Средние показатели не всегда подводят к верным выводам, источником достоверной научной информации они становятся лишь только тогда, когда при их вычислении учитывается закон больших чисел. Сущность закона больших чисел заключается в следующем: закономерности совокупностей равномерного состава можно вычислить только при наличии достаточно большого количества данных; точность измерения закономерностей возрастает с увеличением количества элементов объекта исследования; отклонения отдельных явлений от среднего в ту или другую сторону, обусловленные несущественными, случайными обстоятельствами, при большом количестве элементов взаимно компенсируются; эти закономерности можно количественно выразить только в виде средних показателей. Необходимо иметь в виду, что результаты вычисления средних значений можно использовать лишь при нормальном распределении и шкале отношений или хотя бы на равномерной интервальной шкале. Применение в педагогическом исследовании статистических методов включает в себя следующие этапы. Сбор эмпирических данных методами наблюдения, тестирования, эксперимента, анкетирования и других в целях получения количественных сведений о каких-либо явлениях, заполнение математической модели конкретными цифрами. Сводка полученных сведений, нахождение обобщающих числовых данных и их обработка в пределах формальной математической модели. Составление математической модели для последующего описания с помощью цифр существенных свойств изучаемого объекта. Анализ и интерпретация данных, конструирование содержательных педагогических выводов. Имеются три главных раздела статистики: описательная статистика, индуктивная статистика, измерение корреляции. Описательная статистика направлена на то, чтобы описывать, подытоживать и воспроизводить в виде таблиц или графиков данные того или иного распределения, вычислять среднее для данного распределения, его размах и дисперсию. Индуктивная статистика необходима тогда, когда требуется проверить, можно ли распространить результаты, полученные на данной выборке, на всю популяцию, из которой взята эта выборка. То есть, до какой степени можно путем индукции обобщить на большее число объектов ту или иную закономерность, обнаруженную при изучении ограниченной группы в ходе какого-либо наблюдения или эксперимента. Следовательно, индуктивная статистика необходима после получения эмпирических данных, на этапе обобщения и конструирования выводов. Тот раздел статистики, в котором даются правила измерения корреляции, необходимо применять с целью изучения степени связи между собой двух переменных с тем, чтобы можно было предсказывать возможные значения одной из них, если известна другая. Степень корреляции значений двух переменных может быть вычислена двумя способами: с применением параметрических и с помощью непараметрических методов (тестов). Наиболее широкое применение находят параметрические методы. Название «параметрические» методы возникло от того, что при этом методе сравнивают параметры распределения средних показателей таких, как среднее значение или дисперсия данных. Непараметрические методы используются в том случае, когда исследователь имеет дело с очень малыми выборками или с качественными данными; их достоинство в простоте расчетов и применения. Обоснованный выбор как параметрических методов, так и непараметрических в процессе педагогического исследования во многом определен полученными экспериментальными данными. Данные в статистике – это основные элементы, подлежащие анализу. Данными могут быть количественные результаты, любая информация, которая может быть классифицирована или разбита на категории с целью обработки. Существуют три вида статистических данных. Количественные данные, получаемые при измерениях (например, данные о весе, размерах, температуре, времени, результатах тестирования), их можно распределить по шкале с равными интервалами. Порядковые данные, которые получаются при упорядочивании количественных данных в возрастающей последовательности (1-й, ..., 7-й, ..., 100-й, ...; А, Б, В, ...). Качественные данные, представляющие собой свойства, признаки элементов выборки или популяции. Их нельзя измерить, и единственной их количественной оценкой служит частота встречаемости (число учащихся башкир, татар, русской национальности и др.; учителя со средним специальным, высшим педагогическим образованием, без педагогического образования; учителя мужского и женского пола). Только количественные данные подлежат анализу посредством параметрических методов, в основе которых лежат параметры (такие, например, как средняя арифметическая). Но и то лишь тогда, когда число этих данных достаточно, чтобы проявилось нормальное распределение. Для использования параметрических методов в принципе необходимы три условия: данные должны быть количественными, их число должно быть достаточным, а их распределение – нормальным. Во всех остальных случаях всегда рекомендуется использовать непараметрические методы. 2. Описательная статистикаСтатистическая обработка цифровых данных начинается с группировки. Для этого, прежде всего, необходимо расположить данные каждой выборки в возрастающем порядке. Многие данные принимают одни и те же значения, причем одни значения встречаются чаще, другие – реже. Графически распределение можно представить в столбиковые диаграммы. При этом распределение данных по их значениям дает уже больше информации, чем простое представление в виде рядов. Подобную группировку используют в основном лишь для качественных данных, четко разделяющихся на обособленные категории. Количественные данные отличаются от качественных своей многочисленностью и располагаются на непрерывной шкале. Поэтому такие данные предпочитают группировать по классам, чтобы яснее видна была основная тенденция распределения. Группировка по классам заключается в том, что объединяют данные с одинаковыми или близкими значениями в классы и определяют частоту для каждого класса. Способ разбивания на классы и величина частоты каждого класса зависят от того, что именно экспериментатор хочет выявить при разделении измерительной шкалы на равные интервалы. Данные, разбитые на классы по непрерывной шкале, можно представить графически в виде гистограммы, то есть примыкающих друг к другу прямоугольников. Можно строить также полигоны распределения частот, когда отрезками прямых соединяются центры верхних сторон всех прямоугольников гистограммы, а затем с обеих сторон «замыкают» площадь под кривой, доводя концы полигонов до горизонтальной оси § 3. Средние показатели результатовПонятие «среднего» может быть не связано с каким-то цифровым показателем, а представлять обобщенную категорию мышления, например, средний ученик, средний учитель, средняя успеваемость. Но может быть и в цифровой форме, когда отражаются те или иные средние величины совокупности, вычисляются средние величины объема. Средние объема характеризуются тем, что их числовое значение изменяется при изменении значения любого члена совокупности. Обычно в качестве объемного среднего в педагогическом исследовании применяют арифметическое среднее, реже применяют гармоническое, квадратическое и хронологическое среднее. Средние положения или структурные средние характеризуются тем, что изменяются тогда, когда происходят сдвиги в структуре совокупности (изменяется их количество, последовательность). В качестве средних положений применяют главным образом медиану (средний член упорядоченной частоты, по обеим сторонам которого остается равное количество членов) и моду (наиболее часто повторяющееся значение в статистическом распределении частоты). Реже применяют квартилы (распределение частоты на четыре части, в каждой из которых имеется равное количество членов ряда), децилы (делят статистический ряд на десять равных частей). Три квартилы Наиболее простой статистикой «центральной тенденции» совокупности результатов интервального измерения является мода. Модой (доминантой) называется наиболее часто встречающаяся (доминирующая) частота. Мода (Mo) соответствует либо наиболее частому значению, либо среднему значению класса с наибольшей частотой. Необходимо подчеркнуть, что мода представляет собой наиболее частое значение признака, а не частоту этого значения. Мода используется редко, обычно в тех случаях, когда необходимо дать общее представление о распределении Мода необходима там, где требуется быстро охарактеризовать совокупность на основе явления, встречающегося чаще всего. При изготовлении детской мебели, например, за основу берется мода (рост, вес ребенка, встречающиеся в данной возрастной группе чаще всего), а не средние арифметические данные детей. В коротком статистическом упорядоченном ряду моду можно найти «на глаз». Например: 8, 4, 5, 8, 7, 7, 8, 9, 10, 3, 11, 8. Упорядочим этот статистический ряд от меньшего к большему и получим следующий ряд: 3, 4, 5, 7, 7, 8, 8, 8, 8, 9, 10, 11. Чаще всего здесь встречается число 8, следовательно, оно и является модой. Например, в совокупности оценок успеваемости 2, 3, 4, 4, 4, 5, 5 модой является оценка 4, потому что эта оценка встречается чаще других. В некоторых случаях у распределения могут быть две моды. Например, в совокупности 2, 3, 3, 4, 5, 5 модами являются оценки 3 и 5. В этом случае говорят, что совокупность оценок является бимодальной. Большие совокупности оценок рассматриваются как бимодальные, если они образуют полигон частот с двумя вершинами, даже тогда, когда частоты не строго равны. Принято считать, что в случае, когда все значения оценок встречаются одинаково часто, совокупность данных моды не имеет. Например, в совокупности 2, 2, 3, 3, 4, 4, 5, 5 моды нет. Мода, как мера центральной тенденции, имеет следующую интерпретацию. Она является такой характеристикой, т.е. имеет такое значение, которое наилучшим образом «заменяет все значения». Когда заменяют модой любое значение ряда чисел, мы имеем наибольшую частоту совпадений с числами ряда. Следует заметить, что для малых групп часто о такой замене не может быть и речи. Например, группа из 5 учащихся имеет следующую успеваемость 2, 2, 2, 5, 5. Модальный актив группы составляет величину два. Эта цифра точно характеризует успеваемость трех учащихся группы, но является чрезвычайно некорректной в отношении двух других. Медиана (Me) соответствует центральному значению в последовательном ряду всех имеющихся значений. Медиану также, как и квартилы и децилы легко найти на процентной кривой кумулятивной частоты. Медиана, или центральная величина ряда,– это величина члена, приходящего на середину ранжированного ряда, при нечетном числе членов ранжированного ряда медиана соответствует центральной величине ряда. Например, мы имеем следующий ранжированный ряд: 4, 5, 7, 9, 11, 13, 15, 17, 18. В середине данного ряда находится число 11, следовательно, оно и является медианой. Порядковый номер медианы вычисляется по формуле: где N – число членов в ряду. Медиана в интервальном ряду вычисляется по формуле: 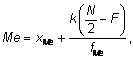 Где xMe – значение нижней границы медианного интервала; k – длина медианного интервала; N – число членов совокупности (åfi при сумме малых частот N = åfi + 1); fMe – частота медианного интервала. Для больших совокупностей данных, где есть объединенные классы, медиана находится следующим образом (смотри таблицу 8). Пусть мы имеем 16 оценок: Таблица 8 Таблица оценок
= 16 Медиана выбирается 8-й и 9-й оценками. По таблице 8 видно, что она располагается в интервале четверок. Поскольку в верхней границе ряда оценок накоплено 4 оценки (1 + 3 = 4), мы должны еще накопить 8 - 4 = 4 частоты, а всего в интервале 8 четверок. Поэтому медиана делит интервал четверок пополам. В интервале между значениями 3,5 и 4,5 лежит 8 четверок. Следовательно, медиана равна 3,5 + 4:8 = 4. Интерпретируем значение медианы на следующем примере. Пусть мы получили следующий ряд оценок 2, 2, 3, 4, 5, 5, 5, где медиана равна оценке 4. Разность между 4 и 2 составляет два, между 4 и 5 минус один. Сумма этих разностей, взятых по абсолютному значению (т.е. без знака), равна 2+2+1+1+1+1 = 8 и всегда меньше суммы разностей относительно любого другого числа данного ряда. В самом деле разности между 5 и другими числами соответственно равны 3, 3, 2, 1, 0, 0, а их сумма абсолютных разностей всех значений относительно медианы всегда меньше суммы разностей относительно любой другой точки. Из этого следует, что если вместо каждой оценки ряда выбрать медиану, то будет допущена минимальная суммарная ошибка. Медиану применяют в том случае, когда хотят определить точную середину ряда. Некоторые интервалы особенно большой частоты могут в значительной мере повлиять на среднее арифметическое. Преимуществом медианы является то, что на нее такие чрезвычайные интервалы не влияют. Центральная тенденция совокупности данных с большими крайними выбросами наилучшим образом характеризуется медианой, когда гистограмма унимодальна. Медиана является одним из членов ряда распределения или, как это бывает в четных рядах, очень близкой к нему величиной. Опираясь на значение медианы, еще точнее на квартилы, можно охарактеризовать структуру ряда вокруг среднего, имеется ли равномерное распределение вокруг среднего, накопление величин по возрастающим или убывающим интервалам. Средняя арифметическая Средняя совокупность значений обозначается Короче эту же самую формулу можно записать следующим образом: Где xi – величина отдельных элементов совокупности; Sfi – количество членов совокупности (объем совокупности). Из формулы следует, что среднее совокупности чисел находится суммированием всех чисел и делением полученной суммы на общее число членов ряда. Смысл (интерпретация) среднего в том, что среднее заменяет все значения в совокупности чисел. Иными словами, взамен каждого значения ряда берется среднее, при этом обеспечивается минимальная ошибка отклонений от среднего. Среднее арифметическое дает возможность охарактеризовать исследуемую совокупность одним числом; сравнить отдельные величины со средним арифметическим; определить тенденцию развития какого-либо явления; сравнить разные совокупности; вычислить другие статистические показатели, так как многие статистические вычисления опираются на средние арифметические. Совокупность характеризуется посредством среднего арифметического в том случае, если распределение параметров расположено симметрично по отношению к середине. При асимметричном распределении или многовершинном полигоне частот среднее арифметическое не подходит для описания совокупности. В таких случаях для характеристики совокупности лучше пользоваться модой. Итак, центральная тенденция распределения частот чаще всего выражается в трех измеряемых средних величинах. Это мода (Mo), медиана (Me) и среднее арифметическое Следует отметить, что каждая мера центральной тенденции числовых рядов измерений и оценки знаний обладает характеристиками, которые ценны в определенных условиях. В малых совокупностях чисел мода, как правило, нестабильна. Например, для совокупности 2, 2, 2, 3, 4, 4 мода равна 2, но если одну из оценок 2 заменить оценкой 4, то мода станет равной 4. Медиана более стабильна. На нее не влияют «большие» и «малые» оценки. Например, для больших совокупностей оценок медиана не изменится, если число минимальных или максимальных оценок резко изменится. Так, например, совокупности 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5 и 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5 имеют одинаковые медианы (Me = 3,5). На величину среднего влияет изменение каждого значения оценки. Для многих числовых совокупностей педагогических измерений мода близка к двум другим мерам – медиане и среднему. Медиана занимает промежуточное положение между модой и средним. Некоторые совокупности результатов педагогических измерений просто не имеют центральной тенденции. Это наблюдается для многомодальных совокупностей оценок (имеющих две и более моды). Например, для совокупностей оценок 2, 2, 2, 2, 2, 4, 4, 4, 4, 4 среднее и мода равна трем, несмотря на то, что даже не существует учащегося с такой оценкой. Ни среднее, ни медиана не в состоянии дать правильного представления об успеваемости этой группы. Более правильное представление об успеваемости этой группы дает словесное описание: «50% в группе имеют оценки «2», а остальные – хорошие». Последнее на языке статистики может быть выражено так: гистограмма бимодальна, т.е. имеет две моды, одна равна 2, другая – 4. § 4. Разброс данных вокруг среднегоРазброс полученных данных в положительную и отрицательную сторону от средней величины обозначается буквой d, а вычисляется через отклонение каждого значения от средней ( Вычисление среднего отклонения проводится следующим образом. Собрав все данные и расположив их в ряд– 3, 5, 6, 9, 11, 14,– находят среднюю арифметическую выборки: Затем вычисляют отклонения каждого значения от средней и суммируют их: -5 -3 -2 +1 +3 +6 (3-8) + (5-8) + (6-8) + (9-8) + (11-8) + (14-8). Но во избежание взаимоуничтожения положительных и отрицательных значений в процессе суммирования общепринято прежде возводить все значения в квадрат, а затем делить всю сумму квадратов на число данных. В нашем примере это выглядит следующим образом: В результате такого расчета получают так называемую дисперсию. Формула для вычисления дисперсии, таким образом, следующая: После этого из дисперсии извлекается квадратный корень. При этом получается так называемое стандартное отклонение: Стандартное отклонение = В данном примере стандартное отклонение равно Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не , а n –1. Стандартное отклонение обозначается греческой буквой s (сигма): Стандартное отклонение показывает, насколько далеко от средней разбросаны результаты в положительную и отрицательную стороны. Укладывается ли этот разброс результатов в стандартное отклонение, которое равно 68% популяции. Итак, описательная статистика необходима для представления графической и количественной оценки степени разброса данных в том или ином распределении. § 5. Индуктивная статистикаСтатистические гипотезы. Статистической гипотезой называется предположение относительно сходства или различия функциональных и числовых характеристик случайных величин или событий. Статистические гипотезы в педагогических исследованиях делят на четыре основные группы: гипотезы о типах вероятностных законов распределения случайных величин; гипотезы о свойствах тех или других числовых параметров; гипотезы о стохастической (вероятностной) зависимости двух или более признаков (факторов); гипотезы о равенстве или различии законов распределения случайных величин, характеризующих изучаемое свойство в двух или более совокупностях рассматриваемых явлений. В математической статистике проверка гипотез о случайных величинах и событиях базируется на принципе так называемой практической невозможности событий. Сущность данного принципа в том, что задается заранее некоторая вероятность a (например, a = 0,1; a = 0,05), именуемая уровнем значимости. При этом случайные события, вероятность которых меньше или равна a, считаются практически невозможными, но если они происходят, то наступление этого рода событий следует рассматривать как неслучайное. Такое событие становится для нас значимым. Выявлена закономерность, согласно которой чем меньше расчетная вероятность осуществления события, тем больше его неслучайность и тем важнее раскрыть принципы этой закономерности. Уровень значимости, выраженный в процентах, показывает сколько раз в ста случаях мы можем ошибиться, объявив изучаемое событие неслучайным. В гуманитарных науках общепринят 5%-й уровень значимости, при котором допускается ошибка в пяти случаях из ста. При более высоком уровне значимости (10%-м) большее число событий нельзя рассматривать как неслучайные, но достоверность такого вывода будет ниже (90% против 95%). Наоборот, более низкий уровень значимости (1%-й; 0,999%-й) приводит к более осторожным, но и более достоверным выводам. Статистическая гипотеза представляет утверждение, которое объективно может оказаться либо истинным, либо ложным. Следовательно, уже на этапе выдвижения гипотезы мы обязаны одновременно мыслить и ее отрицание в форме существования противоположной (альтернативной) гипотезы. Подлежащую контролю гипотезу называют гипотезой частот и нулевой гипотезой и обозначают ее Но. Согласно нулевой гипотезе (Но) существует равенство теоретических вероятностей двух предположений Р1 и Р2. Справедливость гипотезы Но означает, что наблюдаемое различие частот объясняется чисто случайными причинами. Нуль-гипотезе (Но) противопоставляется так называемая альтернативная гипотеза (Н1). Альтернативной гипотезой является рабочая гипотеза научного исследования, согласно которой наблюдаемое различие частот неслучайно, достаточно значимо, обусловлено влиянием независимой переменной. Основной принцип метода проверки гипотез заключается в том, что выдвигается нулевая гипотеза Но с тем, чтобы попытаться опровергнуть ее и тем самым подтвердить альтернативную гипотезу Н1. Соответствующими вычислениями при помощи статистических тестов определяют критерий значимости и по специальным таблицам – границу значимости, если результаты статистического теста, используемого для анализа разницы между средними, окажутся таковы, что позволят отбросить Но – будет означать, что верна Н1, то есть выдвинутая рабочая гипотеза подтверждается. Для того, чтобы судить о том, какова вероятность ошибиться, принимая или отвергая нулевую гипотезу, применяют статистические методы, соответствующие особенностям выборки. Так, для количественных данных при распределениях, близких к нормальным, используют параметрические методы, основанные на таких показателях, как средняя и стандартное отклонение. В частности, для определения достоверности разницы средних двух выборок применяют критерий t-Стьюдента (Госсета), а для того, чтобы судить о различиях между тремя или большим числом выборок, тест F - Снедекора-Фишера, G - Кохрана, критерий Барлета, дисперсионный анализ и др. Если же мы имеем дело с неколичественными данными или выборки слишком малы для уверенности в том, что популяции, из которых они взяты, подчиняются нормальному распределению, тогда используют непараметрические методы – критерий Кроме того, выбор статистического метода зависит от того, являются ли выборки, средние которых сравниваются, независимыми (т.е., например, взятыми из двух разных групп испытуемых) или зависимыми (т.е. отражающими результаты одной и той же группы испытуемых до и после воздействия или после двух различных воздействий). § 6. Проблема репрезентативности выборкиЗадача индуктивной статистики – определять, достаточно ли велика разность между средними двух распределений для того, чтобы можно было объяснить ее действие независимой переменной, а не случайностью, связанной с малым объемом выборки, отсутствием репрезентативности. Основная проблема репрезентативности выборки – величина и верность образцов. Величина представленности образцов зависит от степени однородности целого (чем однороднее целое, тем меньше требуется образцов); от численности категорий и классов, на которые подразделяются результаты исследования (чем их больше, тем больше должно быть образцов); от количества работников, привлеченных к исследованию; от финансирования. Выборки называются статистически однородными, если их распределения сходны, а различия между ними пренебрежимо малы. В противном случае, когда различия велики, а сходство пренебрежимо мало, выборки статистически неоднородны. В некоторых случаях исследователю приходится проверять гипотезы об однородности (неоднородности) через параметры, делая определенные допущения о виде распределения. Это делается не просто путем проверки сходства или различия средних арифметических значений, но с учетом того, что все распределения (кроме Пуассона) имеют два или больше параметров, к примеру, нормальное распределение Гаусса и гамма-распределение, которым следуют многие психологические и педагогические явления, являются двухпараметрическими. Поэтому вместо простой гипотезы о сходстве (различии) двух функций распределения необходимо проверять сложную гипотезу о сходстве двух средних арифметических и одновременно о сходстве двух дисперсий. Только такая гипотеза может быть адекватной в этом случае. Размер выборки находится в зависимости от размера генеральной совокупности, подлежащей изучению, а также цели исследования. Когда цель исследования заключается в изучении состояния знаний ограниченного количества учащихся, например, одного класса, объем выборки не может превысить численность этого класса. В отдельных случаях объем выборки может быть меньше численности учащихся класса из-за того, что не учитываются результаты новеньких в данном классе, пропустивших много занятий по болезни. При изучении больших по объему совокупностей проблема отбора решается с учетом количественной и качественной представительности выборки, это называется требованием репрезентативности. Во-первых, необходимо определить минимальное число объектов, необходимых для того, чтобы при измерении их характерных особенностей начал действовать закон больших чисел, что именуется условием массовости выборки. Соблюдение данного условия необходимо для получения надежных выводов. Во-вторых, необходимо обдумать соблюдение качественной представительности выборки. Под качественной представительностью выборки понимается подбор такой группы объектов, в которой отражены все основные свойства генеральной совокупности. Репрезентативная выборка имеет достаточно большой объем и отражает основные свойства генеральной совокупности. Требование репрезентативности соблюдается лишь при случайном отборе объектов в выборке. Метод случайного отбора характеризуется двумя отличительными особенностями: 1) каждый объект генеральной совокупности имеет одинаковый шанс быть избранным, 2) отбор одного объекта не имеет никакого влияния на отбор какого-либо другого объекта. К этим методам относятся следующие: простой случайный отбор, отбор методом случайных чисел, стратифицированный отбор, систематический отбор. Простой случайный отбор применяется, когда выборка составляется из совокупности небольшого объема. В этом случае каждому элементу совокупности присваивается порядковый номер. Все номера записываются на одинаковые карточки, которые тщательно перемешиваются. Затем выбирается число карточек, требуемое объемом выборки. Выборку составят те объекты, чьи порядковые номера оказались на вынутых карточках Отбор методом случайных чисел отличается от предыдущего только процессом отбора карточек. При отборе карточек применяется таблица случайных чисел. С любого места таблицы выписываются столько случайных чисел, сколько объектов необходимо взять в выборку. Те объекты, порядковые номера которых соответствуют этим числам, составят нужную выборку. Данный метод отбора учащихся непригоден при объеме генеральной совокупности больше тысячи учащихся в виду большой сложности в организации и финансового обеспечения усилий многих людей. Стратифицированный отбор. В процессе исследования бывает необходимо учитывать некоторые качественные или количественные характеристики отдельных групп изучаемой совокупности. Например, требуется исследовать учащихся младших, средних и старших классов, а также учащихся с плохой, средней и хорошей успеваемостью, с учетом места жительства в городе или сельской местности. Во избежание увеличения объема выборки стратифицированный отбор предполагает обследование каждой из этих групп учащихся в отдельности с последующим объединением результатов обследования. Стратификация есть деление генеральной совокупности на однородные по одному или нескольким признакам группы (страты). Если затем из каждой группы пропорционально ее объему отбирается нужное число объектов, то выборка будет качественно представительной для данной совокупности. Этот способ называется пропорциональным стратифицированным отбором. Методика стратифицированного отбора включает в себя три этапа: 1) деление совокупности на типические группы (страты), 2) составление случайной выборки из каждой страты, 3) объединение статистических оценок, полученных по каждой выборке, в составную статистическую оценку, взвешенную пропорционально объему страт. Систематический (систематизированный, интервальный) отбор. Метод систематического отбора заключается в том, что выборку из совокупности производят путем отбора объектов через фиксированный интервал, что можно применить при исследовании упорядоченных объектов (например, пачка тетрадей с контрольными работами), или переписанных объектов (список фамилий учащихся). Если известен объем совокупности (N) и объем выборки (), величина интервала (k) устанавливается следующим образом: Величина интервала будет равна отношению N к n. Величина интервала может быть установлена произвольно, когда одно из этих чисел неизвестно. Использование метода систематического отбора может привести к ошибочным выводам, если объекты совокупности расположены в циклическом порядке (например, в стопке тетрадей контрольные работы каждого класса сложены по оценкам: сначала отличные работы, затем хорошие, посредственные и неудовлетворительные). При совпадении величины интервала отбора с периодом цикла в выборку могут попасть объекты (например, посредственные работы), которые составят непредставительную выборку. К неслучайным методам выборки относятся бессистемный отбор, доступная и целенаправленная выборка. Бессистемный отбор заключается в изучении объектов, случайно встретившихся исследователю. Доступная выборка составляется из объектов, изучение которых находится в возможностях исследователя, от предыдущего отличается систематизированностью. Целенаправленная выборка составляется в тех случаях, когда исследователь прибегает при отборе объектов измерения к помощи лица, хорошо знающего всех членов совокупности (например, учителя или директора). В процессе педагогического исследования невозможно устранить влияние всех случайных или не подлежащих изучению факторов на конечные результаты. Очень большое множество как объективных, так и субъективных факторов оказывают воздействие в ходе эксперимента на те или иные стороны учебно-воспитательного процесса. Это влияние может быть ограничено, если при составлении выборки учащихся будут соблюдаться следующие условия: объем выборки устанавливается в зависимости от цели исследования и должен составлять достаточно большую часть объема той совокупности, которая подлежит изучению; объекты измерения (учащиеся, школы) должны быть максимально вариативны по состоянию измеряемого признака; объекты измерения должны быть максимально однородны по состоянию общих (не подлежащих изучению) признаков; выводы, полученные на основе изучения репрезентативной выборки, можно распространить на учащихся, не включенных в выборку, если они принадлежат к той же совокупности, из которой сделана выборка. Основные понятия по темеВАРИАНТА [< лат. varians (variantis) – изменяющийся] – в статистике – каждый член ряда чисел. ВАРИАНСА (дисперсия) – показатель разброса (дисперсии) данных, соответствующих среднему квадрату отклонений этих данных от средней арифметической; варианса равна стандартному отклонению, возведенному в квадрат. ВЫБОРКА – это небольшое количество элементов, отобранных с помощью научных методов так, чтобы она была репрезентативной, то есть отражала популяцию в целом. ГЕТЕРОГЕННОСТЬ (выборки) – свойство выборки, данные которой в значительной степени разбросаны на шкале распределения, что проявляется большим стандартным отклонением и свидетельствует о том, что данные сильно отличаются друг от друга. ГИПОТЕЗА СТАТИСТИЧЕСКАЯ – утверждение, касающееся распределения популяции или различия между двумя популяциями, основанное на данных, полученных на выборках из этих популяций; существует в форме нулевой гипотезы и альтернативной гипотезы. ГИПОТЕЗА НУЛЕВАЯ – гипотеза, согласно которой различия между выборками обусловлены только случайностью и не отражают действительных различий между популяциями, из которых взяты эти выборки. Обычно нулевая гипотеза выдвигается с целью ее опровержения в пользу альтернативной гипотезы. ГИПОТЕЗА АЛЬТЕРНАТИВНАЯ – гипотеза, согласно которой различия между выборками являются значимыми, т.е. отражают соответствующее различие между популяциями, из которых взяты эти выборки. Обычно альтернативная гипотеза соответствует рабочей гипотезе исследователя. ГЕНЕРАЛИЗАЦИЯ [< лат. generalis – общий, главный] – обобщение, логический переход от частного к общему; подчинение частных явлений общему принципу. КРИВАЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ – колоколообразная кривая, обладающая симметрией относительно средней и характерная для популяции, подчиняющейся закону нормального распределения. КРИВАЯ КОЛОКОЛООБРАЗНАЯ – кривая, характеризующая распределение большинства количественных данных или результатов. Такую кривую для уровней интеллекта можно получить, исследуя распределение результатов интеллектуального тестирования большой группы лиц. Из подобных кривых видно, что результаты большинства исследуемых группируются вокруг среднего уровня, а по мере удаления в ту или иную сторону от этого уровня число их становится все меньше. Именно это и обусловливает характерную колоколообразную форму кривой. КРИТЕРИЙ СТАТИСТИЧЕСКИЙ – статистический показатель, позволяющий принять или отвергнуть ту или иную гипотезу в зависимости от вероятности того, что различия обусловлены чистой случайностью. МЕДИАНА [< лат. mediana – средняя] в статистике – срединное или центральное значение. МОДА [< лат. modus – мера, образ, способ, правило, предписание] в статистике – величина признака, измерение исследуемого явления, которым соответствует наибольшее число случаев или показаний и которым выражают наиболее часто встречающийся тип данного явления. ОБОБЩЕНИЕ СТАТИСТИЧЕСКОЕ – изучение выводов, которые могут быть распространены на популяцию, исходя из данных, полученных на выборке, а также оценка степени достоверности таких выводов. ОТКЛОНЕНИЕ СТАНДАРТНОЕ – показатель, характеризующий разброс в распределении относительно среднего. ПОПУЛЯЦИЯ (в статистике) – совокупность всех элементов реальной или теоретической группы лиц, предметов и т.п. РЕПРЕЗЕНТАТИВНОСТЬ [< фр. representatif – представительный; показательный] в статистике, в экспериментальных исследованиях – показательность каких-либо наблюдений; соответствие характеристик, полученных в результате частичного (выборочного) обследования какого-либо объекта, характеристикам этого объекта в целом, позволяющее распространить выводы частичного обследования на весь изучаемый объект. СТАТИСТИКА [< нем. statistik < лат. status – состояние] – 1) вид практической деятельности, направленной на сбор, обработку, анализ и публикацию информации, характеризующей количественные закономерности жизни общества в связи с их количественным содержанием; 2) наука, излагающая общие вопросы сбора, измерения и анализа массовых количественных данных; 3) математическая статистика - раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. Вопросы и задания для самоконтроляКаково значение методов сводки и обработки результатов в научном исследовании? Раскройте основные этапы применения статистических методов. В чём сущность главных разделов статистики: описательная статистика, индуктивная статистика, изменение корреляции? В чём заключается проблема репрезентативности выборки в исследовании? |
