НТСиТР_Акимов_учебник. Учебное пособие Надежность технических систем и техногенный риск

• Название: Учебное пособие Надежность технических систем и техногенный риск
• Анкор: НТСиТР_Акимов_учебник.doc
• Дата: 03.02.2017
• Размер: 7.5 Mb.
• Имя файла: НТСиТР_Акимов_учебник.doc
• Тип: Учебное пособие; #1925
• страница: 18 из 27

Рис. 6.8.12. Электрическая схема системы "сеть - электрическая лампочка" (а) и дерево (б) для случая первичных отказов: 1 - сеть; 2 - выключатель; 3 - электролампа; 4 – предохранитель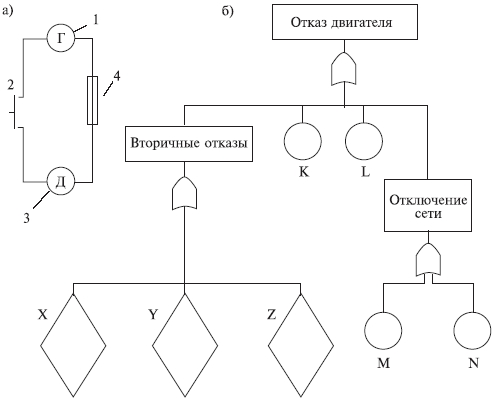



Рис. 6.8.13. Электрическая схема системы "генератор -двигатель" (а) и дерево (б) для случая вторичных отказов: 1 - генератор; 2 - выключатель; 3 - электродвигатель; 4 – предохранитель
Конечное событие может быть вызвано тремя причинами: первичный отказ электродвигателя, вторичный отказ и ошибочная команда (инициированный отказ).

Первичный отказ - это отказ самого двигателя (характеристики которого соответствуют техническим условиям), возникающий в результате естественного старения. Дерево отображает такие первичные события, как отказ выключателя (отсутствие замыкания) К, неисправности внутренних цепей обмотки двигателя L, сети приемника питания М и предохранителя N.

Вторичные отказы возникают из-за причин, которые лежат за пределами, заданными техническими условиями, таких как:

- неправильное техническое обслуживание Х (например, некондиционная смазка подшипников электродвигателя);

- аномальные условия эксплуатации Y, это может быть переработка (например, выключатель остался включенным после предыдущего запуска, что вызвало перегрев обмотки электродвигателя, который, в свою очередь, привел к короткому замыканию или обрыву цепи);

- воздействие на условия работы параметров внешней окружающей среды Z (например, внешняя катастрофа: пожар, наводнение и т.п.).

Вторичные отказы изображаются прямоугольником как промежуточное событие.

Случай инициированных отказов. Подобные отказы возникают при правильном использовании элемента системы, но не в установленное время. Другими словами, инициированные отказы - это сбои операций координации событий на различных уровнях дерева неисправностей: от первичных отказов до завершающего события. Типичным примером является не приведение в действие оператором какого-либо устройства управления (рис. 6.8.14).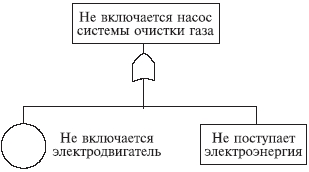



Рис. 6.8.14. Случай инициированного отказа: внесенная неисправность - "не поступает электроэнергия"
Множество деревьев. Для каждой системы возможны различные аварийные ситуации, для каждой из них строят дерево отказов. Впоследствии эти деревья могут быть и связаны. Аналогично, если одна система функционирует в различных режимах, то может понадобиться анализ деревьев отказов для каждого из режимов.

6.9. ДЕРЕВО СОБЫТИЙ - ДС (EVENT TREE ANALYSIS - ЕTA)
Дерево событий - алгоритм рассмотрения событий, исходящих от основного события (аварийной ситуации).

Дерево событий (ДС) используется для определения и анализа последовательности (вариантов) развития аварии, включающей сложные взаимодействия между техническими системами обеспечения безопасности. Вероятность каждого сценария развития аварийной ситуации рассчитывается путем умножения вероятности основного события на вероятность конечного события. При его построении используется прямая логика. Все значения P очень малы. Дерево не дает численных решений.

ПРИМЕР. Допустим, путем выполнения ПАО было выявлено, что критической частью реактора, т.е. подсистемой, с которой начинается риск, является система охлаждения реактора; таким образом, анализ начинается с просмотра последовательности возможных событий с момента разрушения трубопровода холодильной установки, называемого инициирующим событием, вероятность которого равна PA (рис. 6.9.1), т.е. авария начинается с разрушения (поломки) трубопровода - событие A. Далее анализируются возможные варианты развития событий (B, C, D и E), которые могут последовать за разрушением трубопровода. На рис. 6.9.1 изображено дерево исходных событий, отображающее все возможные альтернативы. На первой ветви рассматривается состояние электрического питания. Если питание есть, следующей подвергается анализу аварийная система охлаждения активной зоны реактора (АСОР). Отказ АСОР приводит к расплавлению топлива и к различным, в зависимости от целостности конструкции, утечкам радиоактивных продуктов.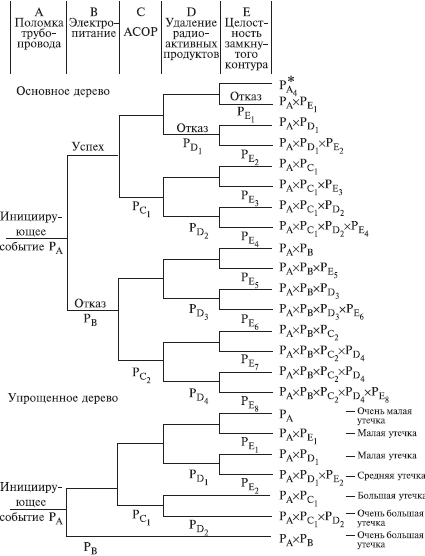



Рис. 6.9.1. Дерево событий
Для анализа с использованием двоичной системы, в которой элементы либо выполняют свои функции, либо отказывают, число потенциальных отказов равно 2N-1, где N - число рассматриваемых элементов. На практике исходное дерево можно упростить с помощью инженерной логики и свести к более простому дереву, изображенному в нижней части рис. 6.9.1. В первую очередь представляет интерес вопрос о наличии электрического питания. Вопрос заключается в том, какова вероятность PB отказа электропитания и какое действие этот отказ оказывает на другие системы защиты. Если нет электрического питания, фактически никакие действия, предусмотренные на случай аварии с использованием для охлаждения активной зоны реактора распылителей, не могут производиться. В результате упрощенное дерево событий не содержит выбора в случае отсутствия электрического питания, и может произойти большая утечка, вероятность которой равна PA(PB. В случае, если отказ в подаче электрической энергии зависит от поломки трубопровода системы охлаждения реактора, вероятность PB следует подсчитывать как условную вероятность для учета этой зависимости. Если электрическое питание имеется, следующие варианты при анализе зависят от состояния АСОР. Она может работать или не работать, и ее отказ с вероятностью PC1 ведет к последовательности событий, изображенной на рис. 6.9.1. Следует обратить внимание на то, что по-прежнему имеются различные варианты развития аварии. Если система удаления радиоактивных материалов работоспособна, радиоактивные утечки меньше, чем в случае ее отказа. Конечно, отказ в общем случае ведет к последовательности событий с меньшей вероятностью, чем в случае работоспособности. Рассмотрев все варианты дерева, можно получить спектр возможных утечек и соответствующие вероятности для различных последовательностей развития аварии (рис. 6.9.1). Верхняя линия дерева является основным вариантом аварии реактора. При данной последовательности предполагается, что трубопровод разрушается, а все системы обеспечения безопасности сохраняют работоспособность.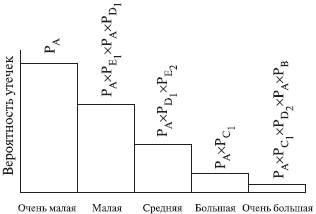



Рис. 6.9.1. Гистограмма вероятностей для различных величин утечек

6.10. ДЕРЕВО РЕШЕНИЙ
Дерево решений является разновидностью дерева событий. В дереве событий рабочие состояния системы не рассматриваются, так что сумма вероятностей всех событий не равна единице. В дереве решений все возможные состояния системы необходимо выразить через состояния элементов. Таким образом, все состояния системы взаимно увязаны, и их вероятность в сумме должна равняться единице. Деревья решений могут использоваться, если отказы всех элементов независимы или имеются элементы с несколькими возможными состояниями, а также есть односторонние зависимости. Они не могут использоваться при наличии двусторонних зависимостей и не обеспечивают логического анализа при выборе начальных событий.

ПРИМЕР. На рис. 6.10.1 показана система последовательно соединенных элементов, которая включает насос и клапан, имеющие соответственно вероятности безотказной работы 0,98 и 0,95, а также приведено дерево решений для этой системы. Следует отметить, что согласно принятому правилу верхняя ветвь соответствует желательному режиму работы системы, а нижняя - нежелательному. Дерево решений читается слева направо.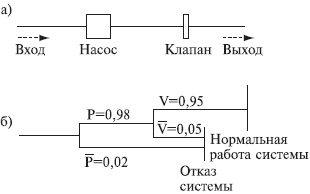



Рис. 6.10.1. Принципиальная схема (а) и дерево решений (б) для двухэлементной системы
Если насос не работает, система отказывает независимо от состояния клапана. Если насос работает, с помощью второй узловой точки изучается вопрос, работает ли клапан.

Вероятность безотказной работы системы: 0,98(0,95=0,931. Вероятность отказа: 0,98(0,05+0,02=0,069, а суммарная вероятность двух состояний системы равна единице.

Этот результат можно получить другим способом с помощью таблицы решения, которая для насоса и клапана имеет вид: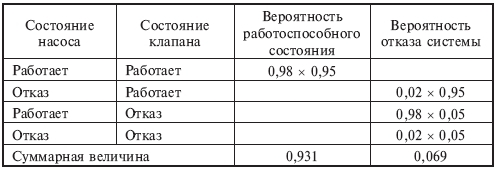



6.11. ЛОГИЧЕСКИЙ АНАЛИЗ
Логический анализ опасностей базируется на понятиях булевой алгебры (алгебры логики).

В алгебре логики переменные, обозначаемые заглавными буквами, имеют, как правило, смысл некоторых событий или факторов. Например, можно обозначить символом А событие, состоящие в повреждении какой-то части машины. Если это происходит, то мы говорим, что А=Т или что А истинно. Если это событие не происходит, говорим, что А=F или что А ложно. Такие высказывания справедливы для некоторого определенного интервала времени и вероятности, связанной с появлением события. Переменные в алгебре логики принимают два значения: истина или ложь (появление или непоявление). Аналогично и функции принимают два значения в зависимости от комбинации логических переменных. Функции образуются с помощью операций И, ИЛИ и НЕ. Смысл этих операций определяется таблицами истинности.

Истинное значение функции задается значениями переменных, входящих в нее. Например, пусть функция А имеет вид
А = ВС + D.

Чтобы определить истинное значение А, надо знать истинные значения четырех переменных. Вычисление значения отдельных членов ведется в порядке: (1) НЕ, (2) И и (3) ИЛИ. Таким образом, если В=ЛОЖЬ, С=ИСТИНА, D=ИСТИНА и Е=ЛОЖЬ, то, используя таблицы, получим:

А = FT + T = FT + TT = F + T = T.


Порядок вычисления операций может быть изменен применением скобок, причем выражения внутренних скобок вычисляются первыми. Например,

А = В() = F() = F() = F = FT = F.

При определенных навыках такие вычисления производятся достаточно быстро.

Особый интерес представляет применение алгебры логики для анализа предполагаемых производственных опасностей.

ПРИМЕР 1. На новой машине имеется цепной привод, который хоть и имеет защитное устройство, но в данном режиме работы должен быть убран. В нормальном режиме сама цепь работает с большим напряжением. Поэтому можно ожидать, что она быстро изнашивается и периодически рвется. Частицы от другого оборудования, попадая в цепь, также могут привести к ее обрыву. В случае обрыва цепи имеющееся защитное устройство, в зависимости от обстоятельств, может не обеспечить защиту рабочего.

Логическими переменными в этом случае будут:

А - защита цепи убрана;

В - цепь изнашивается и рвется;

С - технологические частицы приводят к обрыву цепи;

D - защита достаточна, чтобы защитить рабочего в любом случае.

Х - соответствует наличию опасной ситуации. Логическая операция примет вид

Х = А +B +C или Х = А + (В + С)

Для предотвращения опасной ситуации нужно, чтобы величина Х не стала истиной. Это имеет место, когда А ложно, D истинно или и В и С ложны одновременно.

Покажем еще пример использования принципов алгебры логики. В частности, применим отождествление истинного события с единицей, а ложного с нулем.

ПРИМЕР 2. При строительстве здания компрессорной станции проводились отделочные работы. Бригада отделочников, численностью пять человек, работала на лесах на высоте 3 м от нулевой отметки. При установке бадьи с раствором леса обрушились. Четыре человека были травмированы. Очевидцы несчастного случая, пострадавшие и должностные лица дали показания, на основании которых были выделены основные факторы несчастного случая.

Обозначим эти факторы логическими переменными (заглавными буквами):

А - леса удовлетворяли техническим условиям (ТУ) и правилам техники безопасности (ПТБ);

B - крановщик был нездоров;

C - нагрузка на леса удовлетворяла ТУ и ПТБ;

D - кран был неисправен;

E - на леса был установлен слишком тяжелый груз;

F - в момент опускания груза производился поворот стрелы;

G - перед началом работы крановщик осмотрел кран;

H - перед началом работы мастер осмотрел леса.

Анализ причин несчастного случая (отказа) при помощи булевых функций выполняют следующим образом. Установив факторы несчастного случая (НС) составляется матричная форма (табл. 6.11.1) для его описания. Если очевидец утверждает, что данный фактор имел место, в соответствующую графу заносят "1", если нет, то "0", при отсутствии адекватной информации делают прочерк "-". Затем составляют функцию алгебры логики (Fал). Для каждого очевидца определяют свою конъюнкцию. Если фактор имел место, то букву записывают в утвердительном значении; если нет - в виде инверсий; при "-" букву опускают. Полученную функцию минимизируют перебором всех эквивалентных формул (либо применяя соответствующие методы) и подвергают анализу, при котором устанавливают основные причины несчастного случая и сопутствующие им факторы.

Таблица 6.11.1

Подготовка данных для составления Fал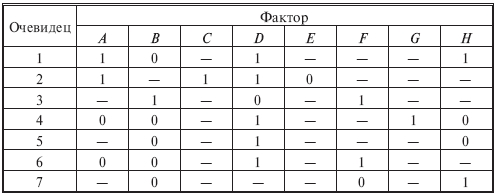



Искомую Fал, для которой X - несчастный случай, запишем в виде

X = ADH+ACD+BF+DG+D+DF+H.

Минимальная формула будет иметь вид

X = BF + D + ACD + FH.

Если несчастный случай произошел, то X=1, т.е. имеет место одна из четырех альтернатив:

- крановщик не был здоров, кран был исправен, был поворот стрелы в момент опускания груза;

- крановщик был здоров, кран был неисправен;

- леса удовлетворяли ТУ и ПТБ, нагрузка на леса удовлетворяла ТУ и ПТБ, груз был установлен на леса в соответствии с требованиями ПТБ;

- кран был исправен, был поворот стрелы в момент опускания груза, мастер осмотрел леса перед началом работы.

Из примеров очевидно, что алгебра логики не отвечает на поставленный вопрос, но дает возможность поставить задачу так, что решение может быть принято при минимальной трудоемкости последующего анализа и сократить количество рассматриваемых подсистем.

6.12. КОНТРОЛЬНЫЕ КАРТЫ ПРОЦЕССОВ
Контрольные карты используются для визуального обнаружения нарушений технологического процесса по измеренным значениям выходной переменной на основе сопоставления ее статистических характеристик с допустимыми (контрольными) пределами. В качестве результатов измерений, наносимых на карты, могут служить любые переменные. Это могут быть скачки потребления электрической мощности, давления, температуры, вибрации и т.д. Построение контрольных карт, в частности определение контрольных пределов, основано на методе проверки статистических гипотез.

Изменения выходной переменной y объекта могут быть вызваны, во-первых, случайными внешними и внутренними возмущающими воздействиями, характерными для нормальной эксплуатации, во-вторых, различного рода нарушениями в работе систем (подсистем, элементов) и ошибочными действиями оператора.

Если переменная y изменяется под влиянием причин только первого вида, то процесс находится под статистическим контролем или в статистически подконтрольном состоянии, т.е. случайные колебания y подчиняются одному и тому же закону распределения вероятности. В случае же появления причин второго вида, процесс выходит из под контроля (находится вне статистического контроля).

На практике наиболее распространены контрольные карты средних значений (карта ), средних геометрических, накопленных сумм, индивидуальных значений y, медиан y_m, комбинированные контрольные карты ( , _y), (y, R_y), (y_m, R_y) и др. (где _y, R_y - соответственно среднее квадратическое отклонение и размах распределения случайной величины y).

Применяемые в картах числовые характеристики случайной величины y рассчитывают по измеренным значениям y_i,1; y_i,2; ...; y_i,N в последовательные моменты времени t_i, i=1,2 ... по методам математической статистики.

На рис 6.12.1 и 6.12.2 приведены карта средних значений и карта ( , R_y). Точками отмечены средние значения _i в моменты времени t_i, i=1,2...; m_y - математическое ожидание распределения случайной величины y. Процесс находится под статистическим контролем, т.е. соответствует нормальному функционированию, если значения _i находятся между нижней и верхней контрольными границами (пределами). Линии и проводят с учетом предполагаемого (допустимого) распределения y или вводят с помощью непараметрического анализа. Когда значение _i выходит за контрольные пределы, это свидетельствует о появлении каких-либо аномальных изменениях в технологическом процессе.

Построение контрольных карт, в частности определение контрольных пределов, основано на методе проверки статистических гипотез.

Различают нулевые и альтернативные гипотезы. К нулевым гипотезам ₀ относят предложения о равенстве нулю статистических показателей при отсутствии различия между сравниваемыми параметрами, например между оценкой среднего и значением математического ожидания m_y распределения случайной величины y. Незначительные отклонения от m_y при правильной гипотезы ₀ могут быть вызваны случайными колебаниями в выборках.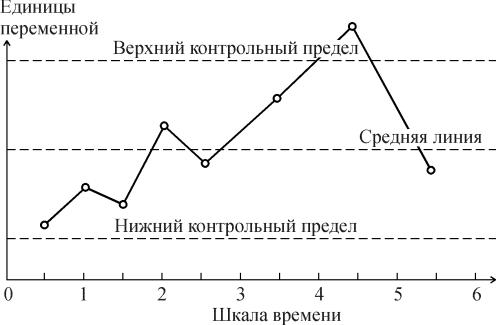



Рис. 6.12.1 Пример контрольной карты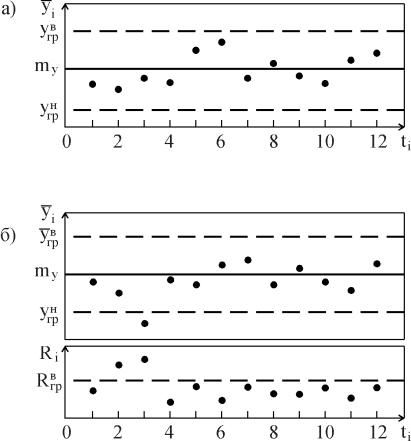



Рис. 6.12.2. Контрольные карты процессов:

а - карта средних значений; б - карта ( , R_y)

К альтернативным гипотезам χ_i, i=1,2,... относятся все остальные гипотезы. Например, нулевой гипотезе о равенстве нулю разности ( -m_y) можно сопоставить две альтернативные: χ₁-( -m_y)>0 иχ₂-( -m_y)<0.

Контрольные границы для карт процессов определяют в следующей последовательности:

1. Выдвигают нулевую χ₀ и одну χ₁ или две χ₁, χ₂ альтернативные гипотезы;

2. Выбирают критическую статистику s;

3. Устанавливают уровень значимости α100%;

4. По таблице квантилей или процентных точек находят граничное значение s_гр (или , ), соответствующее выбранному уровню значимости и числу замеров N;

5. По формуле связи критической статистики s с оцениваемым параметром рассчитывают контрольные границы.

Рекомендации по использованию контрольных карт в разных условиях приведены в табл. 6.12.1

Таблица 6.12.1

Условия применения контрольных карт

Причина изменения процесса	Среднее	Размах R	Стандартное отклонение sy	Накопленная сумма
Грубое отклонение	1	2	-	3
Сдвиг среднего	2	-	3	1
Сдвиг дисперсии	-	1	-	-
Тренд *	2	-	-	1
Колебание	-	1	2	-

Условные обозначения: "-" - неприменима; 1,2,3 - место в ранжированном ряду применения (1 - наиболее предпочтительная карта и т.д.); * систематическое увеличение (уменьшение) средних значений.

6.13. РАСПОЗНАВАНИЕ ОБРАЗОВ
Одно из направлений развития методов контроля надежности элементов системы (или систем), основанных на изучении косвенных параметров, - использование теории распознавания образов. В ней разрабатываются приемы и методы, позволяющие по некоторым, часто весьма незначительным, признакам относить объект изучения к тому или иному классу и охарактеризовать его состояние.

Кластерный анализ - математическая процедура многомерного анализа, позволяющая на основе множества показателей, характеризующих ряд состояний объектов (образов), сгруппировать их в классы (кластеры) таким образом, чтобы объекты, входящие в один класс (образ), были более однородными, сходными по сравнению с объектами, входящими в другие классы. На основе численно выраженных параметров объектов вычисляются расстояния между ними, которые могут выражаться в евклидовой метрике (наиболее употребимой), так и в других метриках.

Кластерный анализ применяют для идентификации опасных состояний системы в том случае, если нарушения в объекте существенно изменяют зависимости выходных переменных от входных воздействий или областей значений переменных.

Обнаружение и диагностирование нарушений при кластерном анализе производят на основе идентификации некоторого образа - кластера - в пространстве нескольких переменных y₁, y₂,..., y_L, соответствующего определенному состоянию работоспособности h, по данным измерения этих переменных. Примеры трех кластеров в области измеряемых значений y₁ и y₂ для состояний работоспособности h₀, h₁, h₂ показаны на рис. 6.13.1. Границы кластеров определяют на основе обработки экспериментальных данных, полученных в различных и известных состояниях работоспособности.

Выделение кластеров отражает различие параметров или вида оператора φ модели объекта при разных состояниях работоспособности, разброс значений y в одном состоянии работоспособности характеризует изменение возмущающих воздействий.

Каждому кластеру соответствует многомерная плотность распределения p(y₁, y₂,..., y_L). Если измеряемые переменные независимы, то функция p(y₁, y₂,..., y_L) равна произведению плотностей распределений p(y_i) переменных y_i, i= :

p(y₁, y₂,..., y_L) = kp(y₁)p(y₂) ... p(y_L),

где k - доля общей совокупности точек, занимаемая данным кластером, kÎ[0; 1].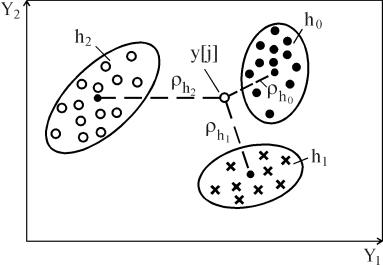



Рис. 6.13.1. Кластеры в пространстве двух переменных для трех состояний работоспособности
Чтобы охарактеризовать кластер по экспериментальным данным, в простейшем случае оценивают параметры распределения математического ожидания m_i, среднего квадратического отклонения σ_i переменной y_i, i= , соответствующие одному состоянию работоспособности, а следовательно, и кластеру, определяют его границу как границу области с назначенной доверительной вероятностью. Если переменные y_i независимы и распределены по нормальному закону, то главные оси кластеров расположены параллельно координатным осям.

Нарушения методами кластерного анализа выявляют следующим образом. В момент времени t_j производят очередное j-е измерение вектора y[j] = (y₁[j],..., y_L[j]). На основе взаимного расположения точки y[j] кластеров в L-мерном пространстве определяют состояние работоспособности h[j] в момент времени t_j. Решение принимают на основе вычисления обобщенного расстояния от проверяемой точки y[j] до центров кластеров. В случае независимости переменных и нормальных распределений обобщенное расстояние ρ_h до h-го кластера определяют по формуле

ρ_h = 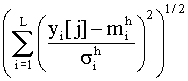, (6.13.1)

где y_i[j] - значение компоненты y_i вектора y[j];

, - параметры распределения ρ_h(y₁,..., y_L) кластера, соответствующего состоянию h объекта.

Точка y[j] относится к тому кластеру, для которого расстояние ρ_h минимально.

Можно также использовать модифицированное обобщенное расстояние ρ''_h, учитывающее фактор k и определяемое по формуле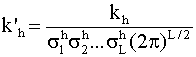

= , , (6.13.2)

где k_h - фактор k для кластера, соответствующего состоянию h.

ПРИМЕР. Объект - химический реактор; контролируются переменные: y₁ - температура, y₂ - концентрация компонента A, y₃ - концентрация компонента B, y₄ – давление; выделены три кластера, соответствующие состояниям: h₀ - нормальное функционирование, h₁ - нарушена подача хладагента, h₂ - не работает мешалка, с параметрами =195, =10, =80, =5, =10, =2, =5, =0,5; =250, =20, =70, =5, =15, =3, =4,8, =0,5; =190, =15, =60, =7,5, =22, =5, =4,7, =0,6 (где σ_i, m_i - среднее квадратическое отклонение и математическое ожидание i-й переменной для ν-го кластера).

При очередном j-м измерении вектора y получены:

y[j] = (y₁[j]=220, y₂[j]=75, y₃[j]=12, y₄[j]=4,9),

обобщенные расстояния ρ_h, вычисленные согласно (6.12.1), которые равны: ρ_h0=2,88, ρ_h1=2,06, ρ_h=3,48. Расстояние ρ_h1 минимально, поэтому y[j] соответствует состоянию h₁.

В ряде случаев пространство значений вектора y содержит определенный кластер. В зависимости от того, какому сектору принадлежит точка y[j], делают вывод о принадлежности ее к соответствующему кластеру, а следовательно, о том, какое состояние работоспособности и нарушение имеет место в рассматриваемый период времени.

Классификационные (разделяющие) линии или функции, которые делят область наблюдаемых значений y на части, соответствующие различным состояниям работоспособности, определяют методами дискриминационного анализа и распознавания образов, например методами случайных плоскостей, потенциальных функций, которые реализуются на ЭВМ.

ПРИМЕР. Имеются два информативных признака: y₁, y₂, по значениям которых определяют состояние или образ объекта. Возможны два состояния работоспособности: h₀ и h₁. Линия L делит область значений y=(y₁, y₂) на две части: Y₀ и Y₁; если yÎY₀, то имеет место состояние h₀, если yÎY₁, то - h₁. В общем случае L - разделяющая плоскость.

Алгоритм построения линии L методом случайной плоскости содержит два этапа и заключается в следующем. На первом этапе проводится серия частных разделяющих линий L_i, i=1,2,... . Для этого берут два первых значения y, принадлежащие разным образам, например y[1]ÎY₀ и y[2]ÎY₁, и проводят произвольную линию L₁, разделяющие точки y[1] и y[2] (рис. 6.13.2,а). Берут следующее значение y[3], для определенности пусть y[3]ÎY₁. Если y[3] и y[2] лежат в одной полуплоскости относительно L₁, то новой линии не проводят; если же y[3] находится в одной полуплоскости с y[1]ÎY₀, то проводят линию L₂, отделяющую y[3] от y[1] (рис. 6.13.2,б). Далее рассматривают значение y[4]. При y[4]ÎY₀ проводят линию L₃, отделяющую y[4] от y[2]ÎY₁ (рис. 6.13.2,в), и т.д. Первый этап заканчивается, когда будут введены все значения y[j], предназначенные для построения разделяющей линии. На втором этапе стирают те участки частных линий L_i, по обе стороны которых имеются одноименные точки, оставшиеся участки образуют разделяющую линию L (рис. 6.13.2,г).

В случаях, когда нельзя указать резкие границы, отделяющие области значений y, соответствующие различным состояниям работоспособности, используют математический аппарат нечетких множеств. В нечетком множестве его элементы имеют различную степень принадлежности к данному множеству. Это объясняется невозможностью полного и четкого описания различных ситуаций, неточностью измерения входных и выходных переменных объекта и т.д.

Нечеткое множество A элементов некоторого множества Y определяют как совокупность упорядоченных пар (кортежей), составленных из элементов yÎY и степеней принадлежности μ_А(y)Î[0; 1], т.е. A={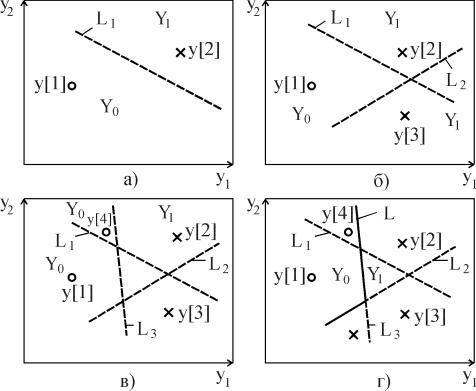А(y)>, yÎY, μ_А(y)Î[0; 1]} (где Y - область определения принадлежности μ_А).



Рис. 6.13.2. Схемы построения разделяющей линии методом случайных плоскостей:

а - два измерения; б - три измерения; в - четыре измерения; г - разделяющая линия L:

о - измерения y[j]ÎY₀; х - измерения y[i]ÎY₁
Чем выше значение μ_А(y), тем больше элемент y соответствует множеству А.

Например, y - температура в работающем химическом реакторе, yÎY={y₁, y₂, y₃, y₄, y₅}, y_ii+1; А - нечеткое множество значений температур, соответствующих аварийной ситуации, равное

А = {(y₁; 0), (y₂; 0), (y₃; 0,3), (y₄; 0,9), (y₅; 1)}.

Данное множество означает, что температуры y₁, y₂ не соответствуют аварийной ситуации, y₃ - мало соответствует, y₄ - вполне соответствует, а при температуре y₅ аварийная ситуация не вызывает сомнения.

Теория нечетких множеств позволяет создавать автоматизированные системы предотвращения аварий, с помощью которых на основе информации с большой неопределенностью, нечетких действий и команд операторов определяют аварийную обстановку и выполняют необходимые защитные действия.

6.14. ТАБЛИЦЫ СОСТОЯНИЙ И АВАРИЙНЫХ СОЧЕТАНИЙ
Безаварийность системы можно повысить, постоянно замеряя переменные технологического объекта с последующим определением состояния работоспособности, его места на дереве отказа. По достижению объектом угрожающих (предаварийных) состояний своевременно принимают необходимые защитные меры. Для этого широко используют таблицы состояний и аварийных сочетаний.

При разработке таблицы определяют измеряемые переменные, устанавливают пределы их измерения (уровни), выбирают виды входных воздействий, при которых измеряются переменные, составляют перечень ситуаций, образуемых сочетаниями и значениями измеряемых переменных, определяют возможные отказы (нарушения) элементов объекта, устанавливают соответствие между ситуациями и отказами, строят дерево решений, выбирают вид и заполняют таблицу решений, проводят работы по компактному представлению таблицы.

Например, в аппарате контролируются давление (y1) и температура (y2). Переменная y1 может находиться на двух уровнях: "0" - нормальное значение, "+" - завышенное значение, а переменная y2 на трех уровнях: "0", "+" и "-" (заниженное значение). В этом случае число возможных ситуаций равно шести (2(3): ситуация 1 - y1=0, y2=0, т.е (0;0); ситуация II - (0;+) и т. д. (табл. 6.14.1). Основные нарушения элементов объекта: 1 - отказ регулятора давления, 2 - отказ регулятора температуры, 3 - отказ регулятора расхода, 4 - не подается пар в рубашку.

Таблица 6.14.1

Таблица решений по значениям двух переменных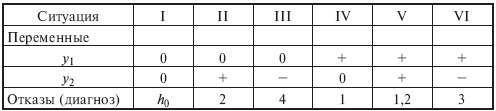



Соответствие между ситуациями и отказами отражается на дереве состояний (рис. 6.14.1). При его построении из начальной вершины (нулевой уровень) проводят ребра, соответствующие значениям переменной y1, из вершины следующего уровня - значениям переменной y2. после рассмотрения всех переменных образуются вершины, соответствующие возможным ситуациям, они пунктиром связаны с отказами объекта.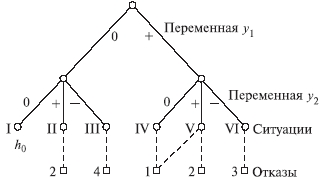



Рис. 6.14.1 Дерево состояний

Преобразование таблицы состояний к компактному виду рассмотрим на примере системы контроля и управления промежуточной емкостью (рис. 6.14.2).Приборы 1, 2 контролируют скорости входного F1 и выходного F2 потоков, регулятор 3 поддерживает постоянный уровень в емкости с помощью вентиля 4. Измеряемыми переменными являются F1,F2 (показания приборов 1, 2) и положение В вентиля 4. Каждая переменная может находиться на трех уровнях: "0" - нормальном; "+" - высоком (вентиль открыт) и "-" - низком (вентиль закрыт). Таким образом, число ситуаций (табл. 6.14.1) равно 33=27.

При функционировании объекта наиболее вероятны следующие нарушения: 2 - течь трубопровода на участке 2-4, 3 - ошибочно открытый байпас вентиля 4 (см. рис. 6.14.2), 4 - забита выходная труба, 5 - течь емкости, 6 - ненормальная производительность и А - аномалия, т.е. невозможная комбинация результатов измерения, с точки зрения принципа работы, ошибочные измерения.

Некоторые ситуации соответствуют одним и тем же отказам, их можно объединить. Так, в ситуациях 2, 11, 20 при различных значениях F1 одинаковый вывод - нарушения 2, 3. Это позволяет объединить три ситуации, отметив значение F1 знаком Л - любое. Результаты объединения ситуаций приведены в табл. 6.14.2.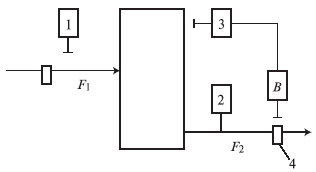



Рис. 6.14.2. Схема системы контроля и управления промежуточной емкостью

Таблица 6.14.2

Таблица решений по значениям трех переменных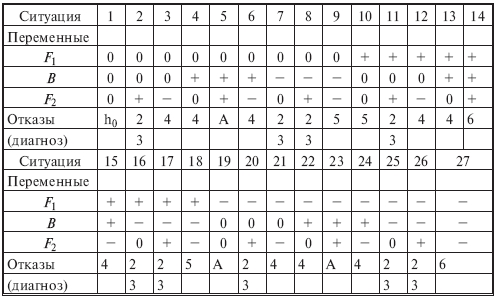


Применение таблицы решений позволяет контролировать развитие аварии, начиная от состояния нормального функционирования, когда все измеряемые переменные находятся в допустимых пределах. Сначала отклоняется от нормы значение одной переменной, затем двух и т.д. С помощью таблицы по значениям переменных определяют конкретные ситуации, а следовательно, и соответствующие им отказы, что позволяет их устранять и принимать меры для предотвращения аварий.

Таблица 6.14.3

Таблица решений с объединенными ситуациями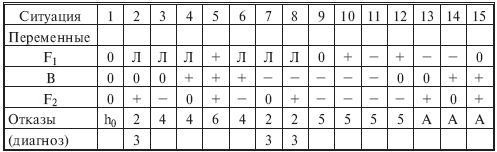


Таблицы решений используют также для автоматизации построения дерева отказов, наряду с ними широко распространены таблицы аварийных сочетаний.