Учебное пособие AnyLogic (1). Учебное пособие по дисциплине имитационое и математическое моделирование Составитель Ремезова Е. М
 Скачать 4.34 Mb.
|
|
Часть 1. Физический маятник Выполнение работы В этом задании мы построим модель маятника. Колебательные движения механических систем широко распространены в технике: качания маятников, движения поршней двигателей внутреннего сгорания, колебания струн, стержней и пластин, вибрации двигателей, фундаментов и множество других подобных процессов. Содержательная постановка задачи Тело единичной массы прикреплено к неподвижному кронштейну с помощью нерастяжимой и несжимаемой нити длиной l. Исследовать колебательные движения тела (рисунок 32). Концептуальная постановка задачи Примем следующие предположения: Объектом исследования является тело массой 1, принимаемое за материальную точку. Движение тела подчиняется второму закону Ньютона. Тело находится под действием трех сил: силы тяжести mg, реакции натяжения нити и силы сопротивления воздуха, пропорциональной квадрату скорости движения. Тело совершает колебательные движения, так как сила тяжести mg уравновешивается вертикальной составляющей реакции натяжения нити. Математическая постановка задачи С математической точки зрения имеем задачу Коши.   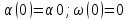 Здесь α - текущий угол отклонения маятника от вертикали, ω - его угловая скорость, μ - коэффициент сопротивления среды (будем считать, что сопротивление среды пропорционально квадрату угловой скорости). Описание модели Н  еобходимо построить модель по вышеприведенным задачам. Модель должна содержать две переменных состояния alpha и omega и три параметра l, mu и g, а также начальное значение переменной alpha, которая задается параметром с именем alpha0. Переменные х и у задают координаты центра масс маятника, их значения можно вычислить по формулам, в соответствии со схемой рисунка 32.В Рисунок 32 Схема маятника корневом объекте модели создайте четыре переменных: х, у, alpha и omega. Переменные х и у следует задать формулами, а alpha и omega. Начальное значение угловой скорости omega равно 0. Четыре параметра l, mu, g и alpha0 так же необходимо создать на диаграмме класса активного объекта. Обратите внимание на уравнение 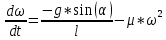 , при возведении ω в квадрат dt член уравнения –μ*ω2 всегда будет отрицательным независимо от направления движения маятника (знака переменной ω), т.е. будет потеряно направление действия силы сопротивления, что приведет к ошибке. Необходимо видоизменить это уравнение так, чтобы знак угловой скорости не потерялся:  Презентация В презентации определите четыре области. В центральной с помощью двух линий и овала нарисуйте маятник. У линии, изображающей нить, один конец всегда имеет координаты (0,0), этот конец нити привязан к неподвижной опоре. Второй конец нити имеет координаты х и у, этот конец нити привязан к маятнику. Соответственно, на закладке Динамические панели свойств линии, отображающей нить, в поле значений координат начала нити X и Y введите 0, в поле значений координат конца нити dX и dY введите величины х и у, рис.7.2. Это приведет к тому, что при работе модели концы отрезка всегда будут находиться в точках с координатами (0, 0) и (x, y). У овала во вкладке с динамическими значениями координат установите х и у.  Рисунок 33 Свойство линии Третья область должна содержать: название модели и небольшой поясняющий текст. Нижняя часть третьей области должна включать два специальных поля для ввода данных: Текстовое поле, более известное как поле редактора или editBox, В эти поля при работе модели можно вводить новые значения параметров l и mu, изменяя их в процессе выполнения модели. В нижней части диаграммы класса активного объекта разместите графики зависимости alpha (ось Y) и omega (ось Y) от времени (Ось X, прописывается как time()), и фазовую диаграмму зависимости alpha (Ось Y) от omega (Ось X). Постройте модель как показано на рисунке 34 и продемонстрируйте ее преподавателю. 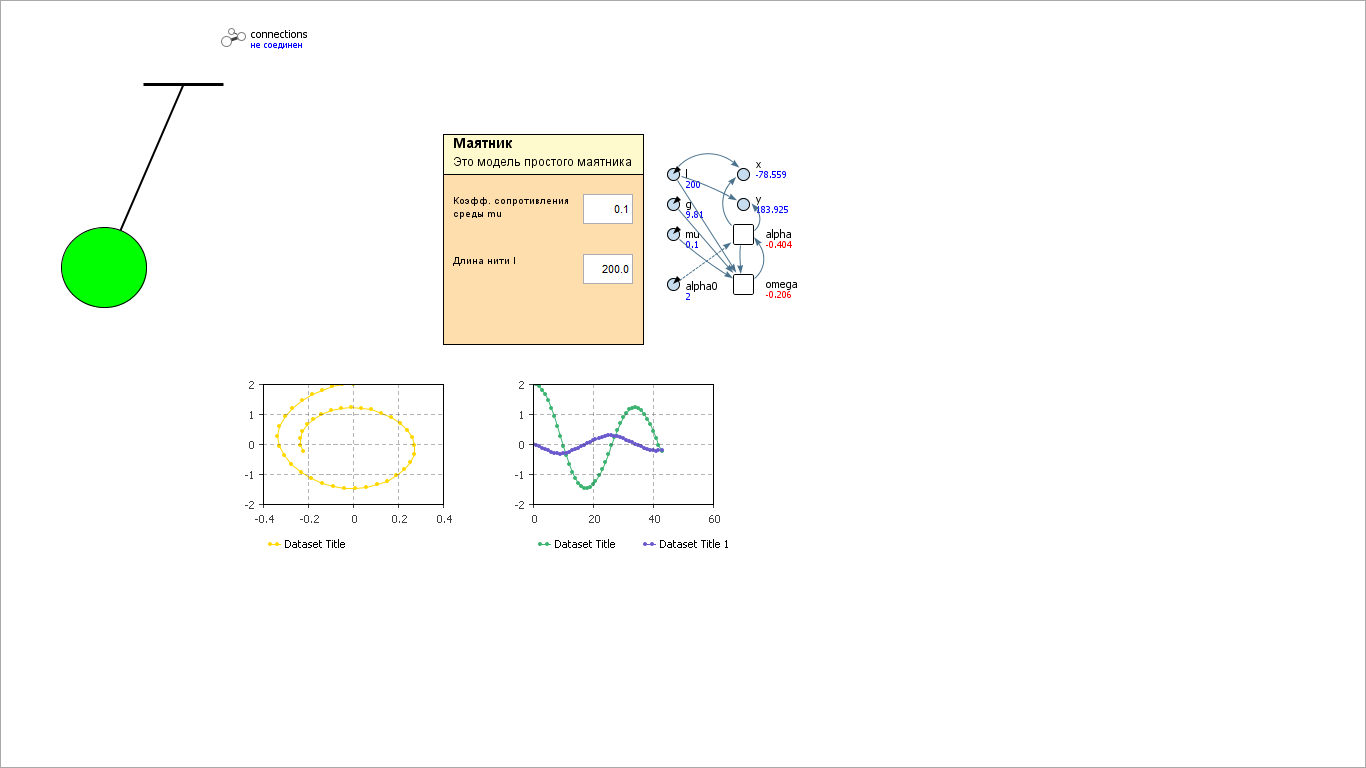 Рисунок 34 Модель маятника Часть 2. Маятник с ограничителем. Выполнение работы В этом задании необходимо построить модель динамической системы, в которой требуется учесть, как непрерывные процессы (движение маятника), так и дискретные события (изменение структуры системы при встрече с ограничителем). Описание проблемы Эта модель является дальнейшим развитием предыдущей модели маятника. Маятник, при соприкосновении нити с ограничителем начинает закручиваться вокруг ограничителя, т.е. в модели появляется второй центр вращения. Уравнения, описывающие движение маятника без ограничителя (на нити длиной L+l) и с ограничителем (на нити длиной l), представлены ниже: Движение без ограничения.    Движение при ограничении    α - текущий угол отклонения маятника от вертикали; ω - его угловая скорость; μ - коэффициент сопротивления среды, пропорциональной квадрату угловой скорости. Начальные условия:   .Описание проблемы Маятник с ограничителем – это система, в которой происходят как непрерывное движение, так и дискретные события, изменяющие характер движения. Такая модель должна содержать уравнения, описывающие непрерывное движение, и стейтчарты, для описания дискретных событий. М  одель должна содержать четыре переменные: х, у, alpha и omega, и шесть параметров: L, l, mu, alphaPin, g и alpha0. Их физический смысл ясен из рисунка 35. Как и в предыдущей модели, alpha0 – начальное значение угла отклонения маятника.П Рисунок 35 Модель маятника оведение маятника описывается стейтчартом с именем Колебания, рисунок 36, с двумя состояниями. В одном состоянии описывается непрерывное движение маятника без ограничения (состояние Без_ограничения), в другом (состояние С_ограничением) – описывается движение вокруг ограничителя. В зависимости от состояния, в котором находится система, переменные х, у и omega будут описываться различными уравнениями.  Рисунок 36 Стейтчарт перехода маятника Условия перехода из одного состояния в другое, а, следовательно, изменение поведения системы определяются следующим образом. Начальное положение маятника задается его углом α0. Маятник соприкасается с ограничителем, если он движется против часовой стрелки (ω >0) и его угол равен αPin или если он движется по часовой стрелке и его угол меньше, чем (2π - αPin). Запишем это на языке Ява в условии перехода из состояния Без_ограничения в состояние С_ограничением: 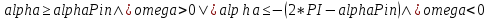 Условие перехода от движения с ограничением к движению без ограничения запишем аналогичным образом:  При соприкосновении с ограничителем и изменении длины нити маятника должна сохраняться его линейная скорость, значит, справедливо соотношение:   Здесь omegaогр и omegaне_огр –угловая скорость маятника при движении с ограничителем и без ограничителя, соответственно. Эти соотношения следует записать в соответствующие поля Действие панели свойств переходов стейтчарта, рисунок 37.  Рисунок 37 Действие при переходе Теперь настало время задать различные формулы для переменных х, у и omega в зависимости от состояния системы. Для этого можно использовать метод класса isStateActive( ). Если модель работает по схеме без ограничения, то вызов метода Колебания.isStateActive(Без_ограничения) вернет значение true. Если модель работает по ограниченной схеме, то вызов этого метода вернет значение false. Откройте свойства переменной omega и в поле d(omega)/dt= запишите следующее условное выражение: Колебания.isStateActive(С_ограничением)?-g*sin(alpha)/l -mu*omega*abs(omega):-g*sin(alpha)/(L+l) - mu*omega*abs(omega) По аналогичному принципу запишите уравнения для переменных х и у. Для переменной alpha – уравнение в обоих состояниях остается неизменным. Презентация Презентацию в этой модели следует построить так же, как и в предыдущей модели простого маятника. Координаты (Х, Y) ограничителя, который задается овалом, определены так: X: L*sin(alphaPin) Y: L*cos(alphaPin) Для отрисовки нити следует использовать два отрезка. Один отрезок анимирует движение нити L, другой отрезок анимирует движение нити l. Координаты начала нити L строятся точно также, как и в предыдущей лабораторной работе. А вот координаты конца нити L (или начала l) строятся иначе, заметьте, что в этих точках нити соединяются и их координаты будут одинаковы – это точка излома. Координаты точки излома зависят от того по какой схеме (ограниченной или не ограниченной) работает модель в текущий момент. Предположим, что модель работает по схеме без ограничителя, т.е. нить не встречает препятствия. Тогда координату точки излома можно найти так: X: L * sin(alpha), Y: L*cos(alpha) Соответственно, в случае, когда модель работает по схеме с ограничителем, т.е. нить коснулась препятствия и остановилась, координата ее точки излома совпадет с координатой ограничителя: X: L * sin(alphaPin), Y: L*cos(alphaPin) Остается только определить, по какой схеме модель работает в текущий момент. Для этого следует использовать, уже известный, метод класса isStateActive(). Для определения координаты Х конца нити L запишите следующее выражение: L*sin(Колебания.isStateActive(Без_ограничения)? alpha: alphaPin) и аналогично для координаты Y. Координаты конца нити l совпадают с координатами центра овала, т.е. они должны быть x и y, но в свойствах линии требуется указать смещение конца по осям X и Y относительно начала линии. Поэтому, в поле dx: динамических свойств линии L нужно указать не координату x, а разницу между x и координатой начала линии по оси X, т.е.: x - L*sin(Колебания.isStateActive(Без_ограничения)? alpha: alphaPin) Аналогично заполняется поле dy. Достройте презентацию модели, как показано на рисунке 38, и продемонстрируйте построенную модель преподавателю.  Рисунок 38 Модель маятника с ограничением Контрольные задания: Измените модель таким образом, чтобы сила тяжести была направлена вдоль горизонтальной оси. Доработайте презентацию модели таким образом, чтобы при движении вниз маятник был одного цвета, а при движении вверх – другого. Доработайте презентацию модели таким образом, чтобы при зависании маятника в верхней точке траектории он менял цвет. Измените модель таким образом, чтобы сила тяжести была направлена вверх. Доработайте презентацию модели таким образом, чтобы при движении направо маятник был одного цвета, а при движении налево – другого. Доработайте модель таким образом, чтобы маятник сопровождала движущая рядом надпись, показывающая мгновенное значение линейной скорости. Лабораторная работа №4. Модель обработки документов в организации. Для приёма и обработки документов в организации назначена группа в составе трёх сотрудников. Ожидаемая интенсивность потока документов - 15 документов в час. Среднее время обработки одного документа одним сотрудником – tобс = 12 мин. Каждый сотрудник может принимать документы из любой организации. Освободившийся сотрудник обрабатывает последний из поступивших документов. Поступающие документы должны обрабатываться с вероятностью не менее 0,95. Определить, достаточно ли назначенной группы из трёх сотрудников для выполнения поставленной задачи. Аналитическое решение Группа сотрудников работает как СМО, состоящая из трёх каналов, с отказами, без очереди. Поток документов с интенсивностью λ=15(1/час) можно считать простейшим, так как он суммарный от нескольких организаций. Интенсивность обслуживания  . Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным. Граф состояний СМО - это схема "гибели и размножения". Для неё имеются готовые выражения для предельных вероятностей состояний системы: Отношение p = λ/µ называют приведенной интенсивностью потока документов (заявок). Физический смысл, её следующий: величина p представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки. В задаче  .В рассматриваемой СМО отказ наступает при занятости всех трёх каналов, то есть при Pотк = P3. Тогда:  Так как вероятность отказа в обработке документов составляет более 0,34 (0,346), то необходимо увеличить количество сотрудников группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем Pотк:   Теперь  .Таким образом, только группа из шести сотрудников сможет обрабатывать поступающие документы с вероятностью 0,95. Решение задачи в AnyLogic Создайте модель Обработка_документов. Объекты и элементы модели Обработка_документов показаны на рисунке 39. Перетащите их на агента Main, разместите, соедините и установите значения свойств согласно таблице 1. Для ввода исходных данных используйте элемент Параметр, тип первых двух double, а третьего - int: срИнтПост - средний интервал поступления документов, по умолчанию - 4; срВрОбр - среднее время обработки документа, по умолчанию - 12; колСотруд - количество сотрудников, по умолчанию - 3.  Рисунок 39 Модель обработки документов Таблица 1 Объекты и элементы модели ОбрДокументов
Для вывода результатов моделирования используются элементы Переменная, тип которых double: постДокум - количество поступивших документов; обрДокум - количество обработанных документов; верОбр - вероятность обработки документов; верОтказа - вероятность не обработки документов. AnyLogic-модель построена. Выделите в окне Проекты Simulation:Main. На странице Модельное время, выберите из списка Остановить: В заданное время. Введите Конечное время: 600000 (модельное время увеличено в 10000). Режим выполнения: Виртуальное время (максимальная скорость). На странице Случайность установите Фиксированное начальное число (воспроизводимые прогоны) и Начальное число: 1055. Запустите модель. Вы должны получить результаты, приведенные на рисунке 40.  Рисунок 40 Результат решения задачи в AnyLogic7 Вероятность не обработки всех документов верОтказа=0,347, то есть отличается от полученного аналитическим путём решения на 0,001. Хотя это отличие можно отнести на счёт округления до трёх знаков после запятой. Теперь измените количество сотрудников с трёх на шесть. Для этого выделите элемент Параметр с именем колСотруд и установите по умолчанию 6. Всё остальные данные оставьте без изменения. Запустите модель. Вероятность не обработки документов верОтказа=0,053, то есть отличается от полученного аналитическим путём решения на 0,001. Сравнительную оценку можно было бы провести и при проведении расчётов с большим числом знаков после запятой, то есть с большей точностью. Варианты заданий:
Лабораторная работа № 5 Модель обработки запросов сервером |