учебное пособие ТА. Учебное пособие по дисциплине Теория алгоритмов предназначено для студентов Политехнического колледжа НовГУ, обучающихся по специальности 230115 Программирование в компьютерных системах
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
2.3 МЕТОДЫ ПЕРЕБОРА В ЗАДАЧАХ ПОИСКАЗадачи поиска предназначены для определения нахождения элемента, обладающего заданным свойством, в определенной совокупности данных, в частности, в массиве. Линейный поиск. Поиск наибольшего и наименьшего элемента в массиве. Дан ряд чисел 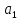 , , 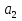 , …, , …, 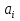 , …, , …, 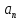 . Разработать алгоритм поиска наибольшего и наименьшего числа в этом ряду с указанием номера (индекса) его расположения. . Разработать алгоритм поиска наибольшего и наименьшего числа в этом ряду с указанием номера (индекса) его расположения.Очевидный способ поиска наибольшего (наименьшего) числа в заданном ряду n чисел включает следующие действия. Взять первое число ряда и сказать, что оно наибольшее (наименьшее), а индекс его равен 1. Затем взять второе число ряда и сравнить с предполагаемым максимальным (минимальным) первым числом. Если второе число больше предполагаемого (максимального) первого числа, взять третье число ряда и сравнить с первым. Так следует действовать до тех пор, пока не будет выбрано последнее 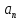 число. В результате на месте первого числа окажется наибольшее (наименьшее) число с указанным его номером в ряду чисел. [2] число. В результате на месте первого числа окажется наибольшее (наименьшее) число с указанным его номером в ряду чисел. [2]Блок – схема алгоритма поиска наибольшего и наименьшего элемента на рис.18. Начало Конец Ввести 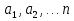 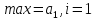 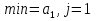 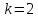 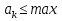 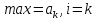 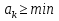 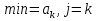 A A 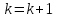 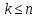 Вывести 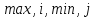 да да да нет нет Рис. 18 Алгоритм нахождения наибольшего и наименьшего элемента в линейном массиве Программа на языке Pascal представлена в Приложении 1, MaxMin.pas. Бинарный поиск. Метод бинарного поиска можно применять уже в отсортированном массиве. Допустим, что массив А отсортирован в порядке не убывания. Это позволяет по результату сравнения со средним элементом массива исключить из рассмотрения одну из половин. С оставшейся частью процедура повторяется. И так до тех пор, пока не будет найден искомый элемент или не будет построен весь массив. [6,7] Рассмотрим алгоритм бинарного поиска на примере. Пример. Пусть X = 6, а массив А состоит из 10 элементов: 3 5 6 8 12 15 17 18 20 25. 1-й шаг. Найдем номер среднего элемента среднего элементов: m= 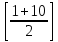 = 5. = 5.Так как 6 < А[5], то далее рассматриваются только элементы, индексы которых меньше 5. 3 5 6 8 2-й шаг. Рассматриваем лишь первые 4 элемента массива, находим индекс среднего элемента этой части : m= 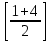 = 2. = 2.6 > А[2], следовательно, первый и второй элементы из рассмотрения исключаются: 3-й шаг. Рассматриваем два элемента, значение m= 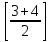 = 3. = 3.А[3] = 6. Элемент найден, его номер – 3. Блок - схема алгоритма бинарного поиска на рис.19: Рис. 19 Алгоритм бинарного поиска в упорядоченном массиве A да нет Вывести: «элемент не найден” A Вывести: «элемент найден», j= 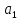 Ввести 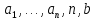 нет Конец Начало нет 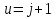 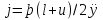 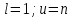 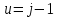 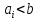 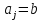 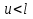 Программная реализация бинарного поиска представлена в Приложении 1, Binar.pas. Случайный поиск. Организация поиска k-го элемента в неупорядоченном массиве Xвозможна следующим образом. Выби рается случайным образом элемент с номером q. Массив Xраз бивается на три части: элементы, меньшие X[q], равные X[q]и большие X[q]. А затем, в зависимости от количества элементов в каждой части, выбирается одна из частей для дальнейшего поиска. Теоретическая оценка числа сравнений имеет порядок k*N, т. е. для худшего случая N2, но на практике он значительно быстрее. |
