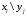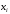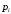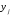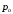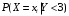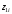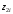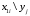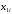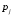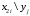Теоритико вероятноостные основы. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЕ_ОСНОВЫ_анализа(1). Учебное пособие Теоретиковероятностные основы комплексного анализа социальноэкономических систем. Типовые задачи продвинутого уровня
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
3. Системы и функции случайных величин как средство комплексного анализа и управления социально-экономическими системами Пример 3.1. (Совместный ряд распределений двумерной дискретной СВ, числовые характеристики, вероятности событий, функции компонент двумерной СВ). Дан совместный ряд распределений системы случайных величин 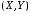 . .
1) Построить ряды распределений СВ, составляющих данную систему, которую также называют двумерной дискретной СВ. Найти числовые характеристики составляющих. 2) Найти вероятности событий: 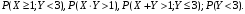 3) Найти условные вероятности событий: 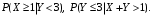 4) Построить условный ряд распределений СВ 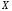 и найти её условные числовые характеристики при условии, что СВ и найти её условные числовые характеристики при условии, что СВ  приняла значение, меньшее трёх. приняла значение, меньшее трёх. 5) Построить ряды распределений СВ 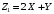 и и 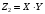 . . 6) Найти коэффициент ковариации (корреляционный момент) СВ  и и  . Найти коэффициент корреляции этих же СВ. Сделать вывод о зависимости СВ . Найти коэффициент корреляции этих же СВ. Сделать вывод о зависимости СВ  и и  . .Решение. 1)Ряд распределений СВ 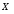 построим, сложив вероятности, стоящие в каждой строке совместного ряда распределений: построим, сложив вероятности, стоящие в каждой строке совместного ряда распределений:
Ряд распределений СВ  построим, сложив вероятности, стоящие в каждом столбце совместного ряда распределений: построим, сложив вероятности, стоящие в каждом столбце совместного ряда распределений:
По известным рядам распределений найдём числовые характеристики СВ  и и  : :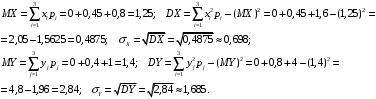 2) Вероятности любых событий можно найти по совместному ряду распределений, сложив вероятности, стоящие в клетках, соответствующих данному событию. Например, событию 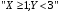 соответствуют 4 клетки совместного ряда распределений, в которых СВ соответствуют 4 клетки совместного ряда распределений, в которых СВ  принимает значения, не меньшие единицы, а СВ принимает значения, не меньшие единицы, а СВ  принимает значения, большие трёх. Сложим вероятности, стоящие в этих клетках. Тогда: принимает значения, большие трёх. Сложим вероятности, стоящие в этих клетках. Тогда: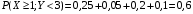 . .Аналогично событию 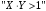 соответствуют 4 другие клетки совместного ряда распределений, в которых произведение СВ соответствуют 4 другие клетки совместного ряда распределений, в которых произведение СВ  и и  принимает значения, большие единицы: принимает значения, большие единицы: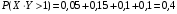 . .Наконец, 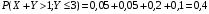 . Если некоторому событию соответствует много клеток в совместном ряде распределений, то сумму вероятностей в них можно найти, воспользовавшись тем, что сумма всех вероятностей в любом (в т.ч. и в совместном) ряде распределений всегда равна единице. Тогда . Если некоторому событию соответствует много клеток в совместном ряде распределений, то сумму вероятностей в них можно найти, воспользовавшись тем, что сумма всех вероятностей в любом (в т.ч. и в совместном) ряде распределений всегда равна единице. Тогда 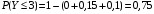 . . 3) Условные вероятности находим по теореме умножения вероятностей, а именно: для любых событий A и B справедливо: 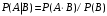 . Тогда: . Тогда: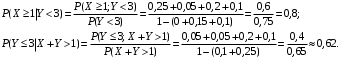 4) Построим условный ряд распределений СВ 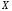 при условии, что СВ при условии, что СВ  приняла значение, меньшее трёх. Сначала найдём необходимые условные вероятности: приняла значение, меньшее трёх. Сначала найдём необходимые условные вероятности: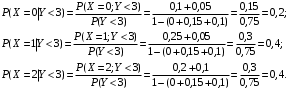 Условный ряд распределений СВ 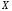 при условии, что СВ при условии, что СВ  приняла значение, меньшее трёх: приняла значение, меньшее трёх:
По этому ряду распределений найдём условные числовые характеристики: 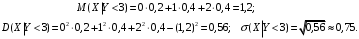 5) Рассмотрим случайную величину 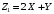 . Перебирая возможные значения СВ, найдём, что СВ . Перебирая возможные значения СВ, найдём, что СВ 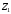 может принять значения 0, 2, 4, 6 и 8. Вероятность каждого значения найдём, как и раньше, сложив вероятности, стоящие в соответствующих клетках совместного ряда распределений. Например, событие может принять значения 0, 2, 4, 6 и 8. Вероятность каждого значения найдём, как и раньше, сложив вероятности, стоящие в соответствующих клетках совместного ряда распределений. Например, событие 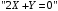 происходит в том и только том случае, если происходит в том и только том случае, если 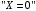 и и 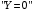 , т.е. этому событию соответствует единственная клетка совместного ряда распределений; вероятность, стоящая в этой клетке, равна 0,1, т.е. , т.е. этому событию соответствует единственная клетка совместного ряда распределений; вероятность, стоящая в этой клетке, равна 0,1, т.е. 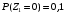 . Аналогично, событие . Аналогично, событие 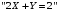 происходит в двух случаях: происходит в двух случаях: 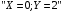 (вероятность 0,05) или (вероятность 0,05) или 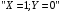 (вероятность 0,25). Тогда (вероятность 0,25). Тогда 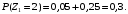 Аналогично найдём вероятности для остальных возможных значений СВ Аналогично найдём вероятности для остальных возможных значений СВ 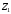 . В результате получим ряд распределений СВ . В результате получим ряд распределений СВ 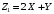 : :
Ряд распределений СВ 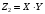 построим аналогично. Возможные значения: 0, 2, 4, 8. Вероятности: построим аналогично. Возможные значения: 0, 2, 4, 8. Вероятности: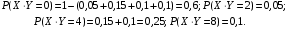 Ряд распределений СВ 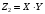 : :
6) Коэффициент ковариации СВ  и и  определяется так: определяется так: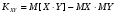 . .Математическое ожидание СВ 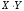 найдём, используя ряд распределений СВ найдём, используя ряд распределений СВ 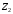 , построенный в предыдущем пункте решения: , построенный в предыдущем пункте решения: 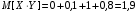 . Математические ожидания . Математические ожидания 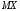 и и 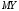 были найдены в первом пункте решения: были найдены в первом пункте решения: 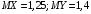 . Тогда коэффициент корреляции, который также называется корреляционным моментом СВ . Тогда коэффициент корреляции, который также называется корреляционным моментом СВ  и и  равен: равен: 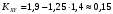 . . С.к.о. СВ  и и  также были найдены в первом пункте решения: также были найдены в первом пункте решения: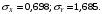 Теперь можно найти коэффициент корреляции случайных величин  и и  : :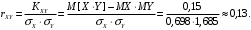 Коэффициент корреляции показывает степень тесноты линейной зависимости между случайными величинами. Его величина всегда лежит между -1 и 1. При наличии жёсткой линейной зависимости, положительной или отрицательной, он равен, соответственно 1 или -1, при полном отсутствии линейной зависимости он равен нулю. Основываясь на полученном значении коэффициента корреляции, можно сделать вывод о наличии слабой положительной линейной зависимости между СВ  и и  . .Пример 3.2. (Построение совместного ряда распределений дискретных СВ, качественный анализ социально-экономической системы с помощью коэффициента корреляции СВ). Три независимых эксперта дают оценку некоторому предложению. Первый эксперт даёт положительную оценку с вероятностью 0,8; второй – с вероятностью 0,5; третий – с вероятностью 0,3. Предложение считается принятым, если за него высказалось большинство экспертов. Рассматриваются 4 дискретных СВ:  – общее число положительных оценок; – общее число положительных оценок; 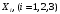 - число положительных оценок, данных первым, вторым и третьим экспертами (последние 3 СВ, очевидно, могут принимать только значения 0 или 1). Требуется подумать в качественном плане над ответом на вопрос, мнение какого эксперта в наибольшей степени влияет на решение, которое будет принято по предложению. Составить совместные ряды распределений трёх двумерных СВ: - число положительных оценок, данных первым, вторым и третьим экспертами (последние 3 СВ, очевидно, могут принимать только значения 0 или 1). Требуется подумать в качественном плане над ответом на вопрос, мнение какого эксперта в наибольшей степени влияет на решение, которое будет принято по предложению. Составить совместные ряды распределений трёх двумерных СВ: 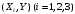 и с помощью их найти коэффициенты корреляции между СВ и с помощью их найти коэффициенты корреляции между СВ 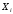 и СВ и СВ  . Сделать вывод о том, мнение какого эксперта в наибольшей степени определяет общее число положительных оценок, а, значит, и на то, будет или не будет принято рассматриваемое предложение. Найти вероятность того, что предложение будет принято. . Сделать вывод о том, мнение какого эксперта в наибольшей степени определяет общее число положительных оценок, а, значит, и на то, будет или не будет принято рассматриваемое предложение. Найти вероятность того, что предложение будет принято.Решение. Качественный анализ ответа на вопрос, мнение какого эксперта в наибольшей степени влияет на решение, которое будет принято по предложению, оставим, пока что, для самостоятельной работы читателя, и приведём этот анализ в конце решения задачи. А сейчас исследуем это вопрос с помощью коэффициентов корреляции СВ. Пусть 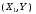 - система двух дискретных СВ (или двумерная дискретная СВ), где - система двух дискретных СВ (или двумерная дискретная СВ), где 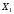 - количество положительных оценок, данных первым экспертом (возможные значения 0 и 1); - количество положительных оценок, данных первым экспертом (возможные значения 0 и 1);  - общее число положительных оценок (возможные значения 0, 1, 2 и 3). Построим совместный ряд распределений этих СВ. Рассмотрим события: - общее число положительных оценок (возможные значения 0, 1, 2 и 3). Построим совместный ряд распределений этих СВ. Рассмотрим события: 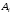 - «i – тый эксперт дал положительную оценку» - «i – тый эксперт дал положительную оценку» 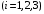 . По условию, мнения экспертов независимы, поэтому события . По условию, мнения экспертов независимы, поэтому события 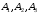 попарно независимы, их вероятности равны 0,8; 0,5 и 0,3 соответственно. Поскольку, попарно независимы, их вероятности равны 0,8; 0,5 и 0,3 соответственно. Поскольку, 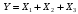 , то несложно определить необходимые вероятности для построения совместного ряда распределений: , то несложно определить необходимые вероятности для построения совместного ряда распределений: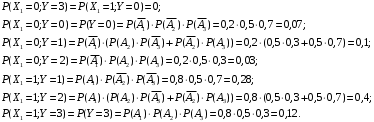 Тогда совместный ряд распределений случайных величин 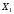 и и  имеет вид: имеет вид:
Ряды распределений СВ 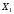 и и  могут быть построены по совместному ряду: могут быть построены по совместному ряду:
Числовые характеристики СВ 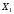 и и  : :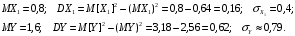 Пусть 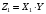 . По совместному ряду распределений . По совместному ряду распределений 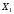 и и  построим ряд распределений построим ряд распределений 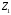 и найдём математическое ожидание: и найдём математическое ожидание:
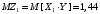 . .Найдём искомый коэффициент корреляции СВ 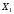 и и  : :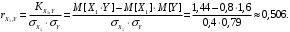 Теперь приведём аналогичные выкладки для двумерных дискретных СВ 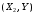 и и 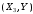 . .Совместные ряды распределений:
Числовые характеристики СВ 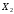 и и 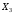 : :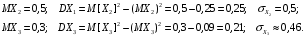 Характеристики произведений компонент двумерных СВ: 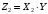 ; ; 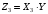 . .
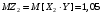 ; ; 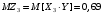 . .Коэффициенты корреляции СВ 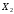 и и 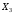 со СВ со СВ  : :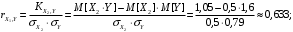 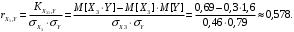 Таким образом, наибольший коэффициент корреляции среди СВ 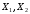 и и 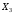 случайная величина случайная величина  имеет со СВ имеет со СВ 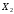 . Соответственно, наибольшее влияние на общее число положительных оценок и на решение по предложению имеет мнение именно второго эксперта. В данной, не очень сложной ситуации этот вывод можно было получить, опираясь лишь на качественные рассуждения. А именно: исходя из условия задачи, первый эксперт почти наверняка даст положительную оценку, третий эксперт, наверное, даст отрицательный отзыв. Поэтому, скорее всего, от первого и третьего экспертов предложение в сумме будет иметь один положительный отзыв. Второй же эксперт не предсказуем. Поэтому с большой долей уверенности можно утверждать, что именно его мнение в итоге и определит, наберёт ли предложение большинство голосов. . Соответственно, наибольшее влияние на общее число положительных оценок и на решение по предложению имеет мнение именно второго эксперта. В данной, не очень сложной ситуации этот вывод можно было получить, опираясь лишь на качественные рассуждения. А именно: исходя из условия задачи, первый эксперт почти наверняка даст положительную оценку, третий эксперт, наверное, даст отрицательный отзыв. Поэтому, скорее всего, от первого и третьего экспертов предложение в сумме будет иметь один положительный отзыв. Второй же эксперт не предсказуем. Поэтому с большой долей уверенности можно утверждать, что именно его мнение в итоге и определит, наберёт ли предложение большинство голосов.Данный пример показывает, что числовые характеристики системы СВ позволяют раскрыть суть социально-экономической ситуации. И в других, более трудных случаях именно расчёт вероятностных характеристик системы СВ позволит провести качественный анализ социально-экономической системы. Пример 3.3. (Совместная плотность распределения двумерной непрерывной СВ, числовые характеристики, вероятности событий, совместное равномерное распределение). Двумерная дискретная СВ 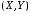 равномерно распределена в треугольнике с вершинами O (0;0), A (0;1) и B (1;0). равномерно распределена в треугольнике с вершинами O (0;0), A (0;1) и B (1;0).1) Записать функцию совместной плотности распределения СВ  и и  . .2) Найти плотности распределения и числовые характеристики компонент системы. 3) Найти вероятность попадания случайной точки 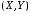 в круг в круг 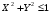 . Найти вероятность события . Найти вероятность события 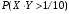 . .4) Найти коэффициент ковариации и коэффициент корреляции СВ  и и  . .Решение: 1) Границы треугольника задаются линиями: 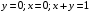 . Вершинами треугольника являются точки O; A и B. Площадь данного треугольника . Вершинами треугольника являются точки O; A и B. Площадь данного треугольника 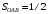 . Поскольку СВ распределена равномерно, то во всех точках данного треугольника значение совместной плотности . Поскольку СВ распределена равномерно, то во всех точках данного треугольника значение совместной плотности 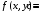 , а вне этого треугольника , а вне этого треугольника 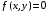 . Отметим также, что на границе треугольника функция плотности распределения может быть не определена. Подобное свойство характерно для любой непрерывной СВ. По свойству плотности распределения: . Отметим также, что на границе треугольника функция плотности распределения может быть не определена. Подобное свойство характерно для любой непрерывной СВ. По свойству плотности распределения: 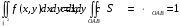 , ,отсюда 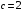 , тогда искомая совместная плотность распределения имеет вид: , тогда искомая совместная плотность распределения имеет вид: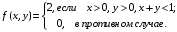 2) Пусть 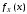 и и 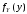 - плотности распределения СВ - плотности распределения СВ  и и  , которые являются компонентами двумерной СВ , которые являются компонентами двумерной СВ 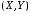 . При любых . При любых  и и 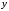 справедливо: справедливо: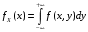 и и 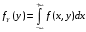 . .Тогда, если 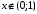 , то , то 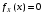 . В противном случае: . В противном случае: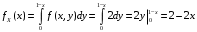 . .Таким образом, плотность распределения СВ  имеет вид: имеет вид: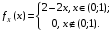 Аналогично для СВ  : :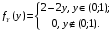 Зная плотности распределения, найдём числовые характеристики СВ  и и  : :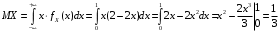 ; ;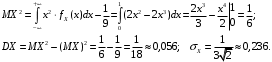 СВ Y имеет такие же математическое ожидание, дисперсию и с.к.о. 3) Вероятность попадания любой СВ X в некоторую область 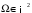 может быть найдена как интеграл от плотности распределения: может быть найдена как интеграл от плотности распределения: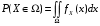 . .Вероятность попадания равномерно распределенной СВ X в некоторую область может быть определена из геометрических соображений. Действительно: если двумерная СВ равномерно распределена на некотором множестве D, то значение плотности распределения в точках этого множества постоянно и равно 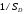 , где , где 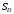 - площадь множества D. Тогда для любого множества - площадь множества D. Тогда для любого множества 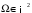 : :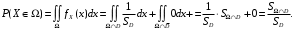 Поэтому вероятность попадания равномерно распределенной СВ X в некоторую область ещё называют геометрической вероятностью. Легко понять, что весь рассматриваемый треугольник OAB лежит внутри круга 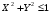 . Поэтому, если D – треугольник OAB, а . Поэтому, если D – треугольник OAB, а 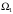 - круг - круг 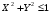 , то , то 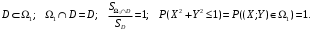 Пусть теперь 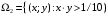 ; D – треугольник OAB, ; D – треугольник OAB, 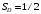 . .Пересечение множеств 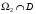 показано на рис.1. показано на рис.1.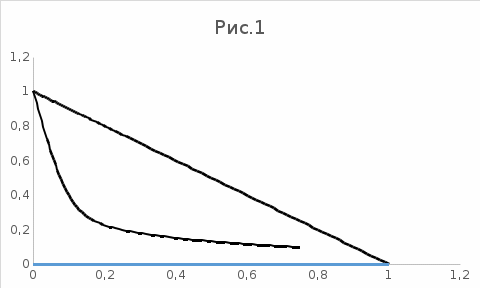 Найдём точки пересечения линий 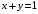 и и 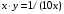 : :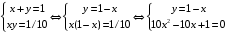 . .Т.е. имеем 2 точки пересечения: 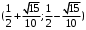 и и 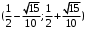 . Площадь множества . Площадь множества 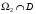 повторный интеграл: повторный интеграл: 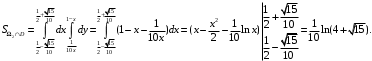 Тогда 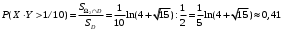 . .4) По определению коэффициентов ковариации и корреляции: 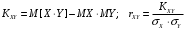 . .Если 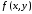 - совместная плотность распределения СВ - совместная плотность распределения СВ  и и  , то , то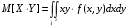 . .Совместная плотность распределения и числовые характеристики СВ  и и  были найдены в первом и втором пунктах решения: были найдены в первом и втором пунктах решения: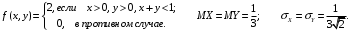 Теперь найдём коэффициенты ковариации и корреляции: Теперь найдём коэффициенты ковариации и корреляции: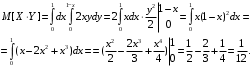 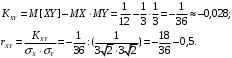 Отрицательное значение коэффициента корреляции означает, что если одна из случайных величин растёт, то другая имеет тенденцию к уменьшению. Несложно понять, что в качественном плане для СВ  и и  такой вывод следует из их совместного равномерного распределения в треугольнике OAB. такой вывод следует из их совместного равномерного распределения в треугольнике OAB. Пример 3.4. (Проведение финансово-экономического анализа на основе изучения совместного распределения показателей экономической системы, совместное нормальное распределение, композиция распределений). Инвестиционный портфель состоит из двух видов ценных бумаг, стоимости которых  и и  имеют совместное нормальное распределение: имеют совместное нормальное распределение: 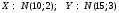 . Параметры указаны в условных единицах. Коэффициент корреляции . Параметры указаны в условных единицах. Коэффициент корреляции 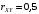 . .1) Найти числовые характеристики общей стоимости портфеля 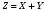 . . 2) Построить совместную плотность распределения СВ  и и  . .3) Найти плотность распределения стоимости портфеля и вероятность того, что эта стоимость будет больше 20. 4) В настоящий момент стоимость второй ценной бумаги в портфеле равна 12. Найти условную плотность распределения, числовые характеристики стоимости первой ценной бумаги и вероятность того, что стоимость первой бумаги больше 7, но меньше 8? Решение. 1) Числовые характеристики найдём по известным формулам, справедливым для любых СВ: 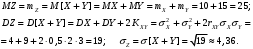 2) Воспользуемся формулой плотности двумерного нормального распределения: 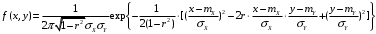 Подставляем исходные данные задачи: Подставляем исходные данные задачи: 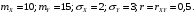 Совместная плотность СВ  и и  имеет вид: имеет вид: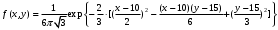 . .3) Сначала найдём функцию распределения СВ Z. Пусть 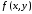 - совместная плотность распределения СВ - совместная плотность распределения СВ  и и  . Тогда: . Тогда: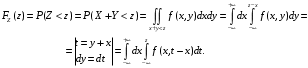 Теперь найдём плотность распределения СВ Z: 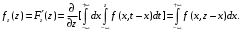 Получена формула плотности распределения суммы двух СВ: 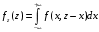 , ,где 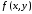 - совместная плотность распределения СВ - совместная плотность распределения СВ  и и  . Эта формула справедлива для любых распределений СВ . Эта формула справедлива для любых распределений СВ  и и  . . Теперь воспользуемся формулой совместной плотности, полученной в предыдущем пункте. Подставим её в последнюю формулу: 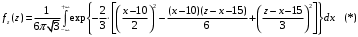 После замена переменной 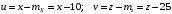 получим формулу плотности суммы нормально распределённых СВ: получим формулу плотности суммы нормально распределённых СВ: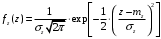 Таким образом показано, что сумма нормально распределённых СВ – это СВ, которая также имеет нормальное распределение. Значения мат. ожидания и с.к.о СВ Z можно найти, проведя до конца преобразования правой части формулы (*), но мы воспользуемся теми же значениями, полученными в первом пункте решения задачи ( 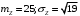 ), тогда имеем: ), тогда имеем: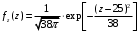 . .По формуле вероятности попадания нормально распределённой СВ на заданный интервал: 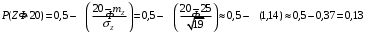 . .4) Стоимость второй ценной бумаги равна 12. Найдём условную плотность распределения стоимости первой бумаги. По теореме умножения плотностей распределения 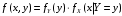 , где , где 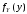 - плотность распределения СВ - плотность распределения СВ  , ,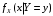 - условная плотность распределения СВ - условная плотность распределения СВ  , при условии, что СВ , при условии, что СВ  приняла значение приняла значение 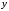 . Тогда . Тогда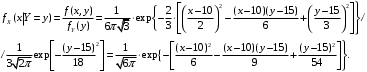 Как видно, условная плотность распределения является также плотностью нормального распределения. Учитывая, что 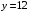 , имеем: , имеем: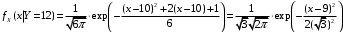 . .Таким образом, при условии, что стоимость второй ценной бумаги равна 12, стоимость первой ценной бумаги есть нормально распределённая СВ, с мат. ожиданием, равным 9 и с.к.о., равным 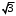 : : 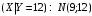 . Тогда . Тогда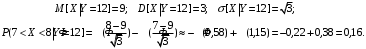 Пример 3.5. (Формирование оптимального портфеля ценных бумаг, числовые характеристики СВ как экономические показатели доходности и риска ценных бумаг, операция «shortsale»). Инвестор формирует портфель ценных бумаг из некоррелированных ценных бумаг четырёх видов. Доходность ценной бумаги, как и доходность всего портфеля, являются случайными величинами. Эффективность ценной бумаги и портфеля понимаются как среднее ожидаемое значение доходности. Риск ценной бумаги и портфеля понимаются как с.к.о. доходности. Параметры ценных бумаг, формирующих в портфель, представлены в таблице:
Определить доли ценных бумаг в оптимальном портфеле минимального риска в зависимости от заданной эффективности портфеля 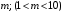 . Найти величину риска . Найти величину риска 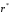 этого портфеля. Определить при каких значениях этого портфеля. Определить при каких значениях 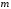 возникает необходимость в проведении операции «short sale». Эта операция состоит в том, что, инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги некоторого вида держателю таких бумаг вместе с доходом, какой они бы принесли их владельцу за это время. За это сейчас от держателя этих бумаг он получает их денежный эквивалент. возникает необходимость в проведении операции «short sale». Эта операция состоит в том, что, инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги некоторого вида держателю таких бумаг вместе с доходом, какой они бы принесли их владельцу за это время. За это сейчас от держателя этих бумаг он получает их денежный эквивалент. Решение. В данном случае в числе ценных бумаг есть безрисковая, при наличии таковой решение выглядит следующим образом. Пусть 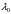 - доля безрисковой ценной бумаги, а - доля безрисковой ценной бумаги, а 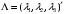 - вектор-столбец долей рисковых ценных бумаг в портфеле. Тогда - вектор-столбец долей рисковых ценных бумаг в портфеле. Тогда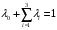 . . Эффективность и риск портфеля определяются как математическое ожидание и с.к.о. суммарной доходности ценных бумаг, составляющих портфель. Пусть 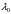 и и 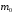 - доля безрисковой ценной бумаги в портфеле и её эффективность, а - доля безрисковой ценной бумаги в портфеле и её эффективность, а 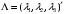 и и 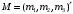 - вектор-столбцы долей рисковых ценных бумаг в портфеле и их эффективностей. Тогда эффективность и риск портфеля определяются так: - вектор-столбцы долей рисковых ценных бумаг в портфеле и их эффективностей. Тогда эффективность и риск портфеля определяются так: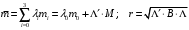 , ,где 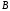 - ковариационная матрица рисковой части портфеля, поскольку доходность безрисковой ценной бумаги имеет нулевую дисперсию и не коррелирована с доходностями остальных ценных бумаг. Математическая модель задача формирования оптимального портфеля при наличии безрисковой ценной бумаги теперь выглядит как задача оптимизации: - ковариационная матрица рисковой части портфеля, поскольку доходность безрисковой ценной бумаги имеет нулевую дисперсию и не коррелирована с доходностями остальных ценных бумаг. Математическая модель задача формирования оптимального портфеля при наличии безрисковой ценной бумаги теперь выглядит как задача оптимизации: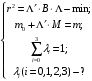 Решив эту задачу обычными методами, получим: 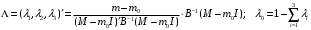 , ,где  - вектор-столбец, все компоненты которого равны 1. - вектор-столбец, все компоненты которого равны 1. Как видно из полученной формулы, соотношение между числами 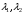 и и 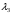 не зависит от заданной эффективности портфеля не зависит от заданной эффективности портфеля 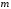 , т.е. структура рисковой части оптимального портфеля не зависит от его эффективности. Она зависит только от характеристик ценных бумаг, которые определяются их рынком. Заметим, что это свойство справедливо только при наличии на рынке и в портфеле безрисковых ценных бумаг. , т.е. структура рисковой части оптимального портфеля не зависит от его эффективности. Она зависит только от характеристик ценных бумаг, которые определяются их рынком. Заметим, что это свойство справедливо только при наличии на рынке и в портфеле безрисковых ценных бумаг.Теперь подставим значения из условия данной задачи:  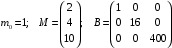 . Тогда . Тогда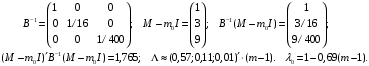 Необходимость в операции «short sale» возникает для безрисковой ценной бумаги, если 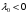 , т.е. при , т.е. при 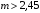 . Заметим, что на рынке обычно проводят операцию «короткой продажи» ценной бумаги, если ожидается снижение её курса. В данном случае, это вовсе не предполагается. . Заметим, что на рынке обычно проводят операцию «короткой продажи» ценной бумаги, если ожидается снижение её курса. В данном случае, это вовсе не предполагается.Риск оптимального портфеля является значением целевой функции решённой задачи оптимизации: 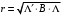 . В данной задаче . В данной задаче 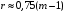 . . Задачи для самостоятельного решения 1. Дан совместный ряд распределений системы случайных величин 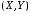 . .
1) Построить ряды распределений СВ, составляющих данную систему. Найти числовые характеристики составляющих. 2) Найти вероятности событий: 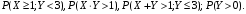 Найти вероятность того, что хотя бы одно решение имеет квадратное уравнение Найти вероятность того, что хотя бы одно решение имеет квадратное уравнение 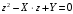 , где , где  - искомая переменная. - искомая переменная. 3) Найти условные вероятности событий: 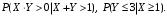 4) Построить условный ряд распределений СВ 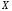 и найти её условные числовые характеристики при условии, что СВ и найти её условные числовые характеристики при условии, что СВ 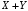 приняла значение, меньшее четырёх. приняла значение, меньшее четырёх. 5) Построить ряды распределений СВ 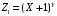 и и 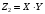 . . 6) Найти коэффициент корреляции СВ  и и  . Сделать вывод о зависимости СВ . Сделать вывод о зависимости СВ  и и  . .2. Поезда приходят на станцию точно по расписанию: 9-30; 10-30;11-30; … 15-30. Однако каждый из поездов с вероятностью 0,2 может по причине неисправности не прийти вовсе. Составить совместный ряд распределений и найти коэффициент корреляции числа поездов, которые действительно приходят на станцию с 9 до 11 часов и с 10 до 12 часов. Найти условные числовые характеристики числа поездов, которые действительно приходят на станцию с 10 до 12 часов, при условии, что с 9 до 11 пришёл 1 поезд. 3. Пассажир едет по маршруту последовательно на двух видов транспорта, времена ожидания которых 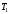 и и 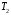 , измеренные в часах, - независимые СВ, равномерно распределённые на интервале (0;1). Построить плотность распределения общего времени ожидания транспорта за время поездки , измеренные в часах, - независимые СВ, равномерно распределённые на интервале (0;1). Построить плотность распределения общего времени ожидания транспорта за время поездки 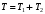 . Найти числовые характеристики и вероятность того, что общее время ожидания будет больше полутора часов. . Найти числовые характеристики и вероятность того, что общее время ожидания будет больше полутора часов.4. Инвестиционный портфель состоит из трёх видов ценных бумаг, стоимости которых  , ,  и и 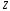 имеют совместное нормальное распределение. Вектор-столбец математических ожиданий СВ имеют совместное нормальное распределение. Вектор-столбец математических ожиданий СВ  , ,  и и 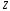 : : 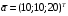 . Ковариационная матрица стоимостей ценных бумаг имеет вид: . Ковариационная матрица стоимостей ценных бумаг имеет вид: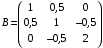 Параметры указаны в условных единицах. 1) Найти числовые характеристики общей стоимости портфеля 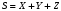 2) Построить совместную плотность распределения СВ  , ,  и и 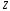 :. :.3) Найти плотность распределения стоимости портфеля и вероятность того, что эта стоимость будет больше 30. 4) В настоящий момент стоимость первой ценной бумаги в портфеле равна 11, стоимость второй ценной бумаги равна 8. Найти условную плотность распределения, числовые характеристики стоимости портфеля ценных бумаг и вероятность того, что стоимость всего портфеля больше 40? Указание. Воспользоваться формулой плотности трёхмерного нормального распределения: 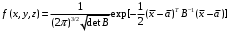 , где , где 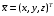 - вектор-столбец переменных. - вектор-столбец переменных.5. Инвестор формирует портфель ценных бумаг из ценных бумаг трёх видов, эффективности которых (в у.е.) 1; 1,5 и 2. Первая ценная бумага безрисковая, а ковариационная матрица доходностей двух рисковых ценных бумаг имеет вид: 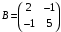 Определить доли ценных бумаг в оптимальном портфеле минимального риска в зависимости от заданной эффективности портфеля 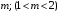 . Найти величину риска . Найти величину риска 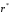 этого портфеля. Определить при каких значениях этого портфеля. Определить при каких значениях 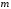 возникает необходимость в проведении операции «short sale». возникает необходимость в проведении операции «short sale».СОДЕРЖАНИЕ Предисловие……………………………………………………………………...…… 3 1. Алгебра событий как основа анализа стохастического характера социально-экономических процессов……………………………………..……….. 4 2. Случайные величины как средства как средство математического описания социально-экономических систем……………………………………... 12 3. Системы и функции случайных величин комплексного анализа социально- экономическими системами………………………………...……………………… 20 |