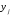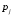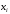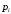Теоритико вероятноостные основы. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЕ_ОСНОВЫ_анализа(1). Учебное пособие Теоретиковероятностные основы комплексного анализа социальноэкономических систем. Типовые задачи продвинутого уровня
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
2. Случайные величины как средство математического описания социально-экономических систем Пример 2.1. (Математическая модель задачи, ряд распределений, числовые характеристики дискретных случайных величин, формула Бернулли). Четыре независимых эксперта дают оценку предложения, сделанного сотрудником фирмы. Известно, что каждый из экспертов даёт положительную оценку подобных предложений сотрудников в 70% случаев. Решение по предложению принимается в соответствии с мнением большинства экспертов. Если мнения экспертов разделились поровну, то приглашается пятый эксперт, который не зависимо от первых двух даёт положительную оценку с вероятностью 0,6. В соответствии с его мнением принимается решение. Составить ряд распределений числа положительных экспертных оценок. Найти математическое ожидание, дисперсию и с.к.о. этого числа. Найти вероятность того, что предложение сотрудника будет одобрено. Решение. В условии задачи нет никаких данных о характере рассматриваемого предложения, есть только сведения о том, как приглашённые эксперты, в целом, оценивают подобные предложения. Поэтому в математической модели данной задачи будут учитываться только сведения об экспертах, как бы рассматривая некоторое «усреднённое» (по качеству) предложение. Пусть дискретная случайная величина X – число положительных оценок сделанного предложения. В дальнейшем словосочетание случайная величина будем в пособии сокращать как СВ. Для построения ряда распределений СВ X рассмотрим другую (вспомогательную) СВ. Пусть дискретная СВ Y – число положительных оценок, сделанных первыми четырьмя экспертами. Поскольку эти эксперты делают свои оценки независимо с одинаковой вероятностью положительных оценок, то Y можно рассматривать как число «успехов» в серии независимых опытов, т.е. в схеме Бернулли. Тогда СВ Y имеет биномиальное распределение с параметрами 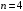 и и 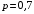 . СВ Y может принимать значения 0, 1, 2, 3 и 4, причём вероятность каждого значения может быть определена по формуле Бернулли: . СВ Y может принимать значения 0, 1, 2, 3 и 4, причём вероятность каждого значения может быть определена по формуле Бернулли: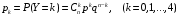 , где , где 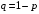 . .Тогда 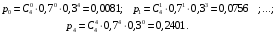 Ряд распределений СВ Y имеет вид:
По условию, если 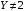 , то , то 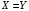 , если же , если же 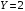 , то значение X зависит от мнения пятого эксперта: , то значение X зависит от мнения пятого эксперта: 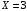 , если его мнение положительно, что происходит с вероятностью 0,6 и , если его мнение положительно, что происходит с вероятностью 0,6 и 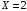 , если его мнение отрицательно что происходит с вероятностью 0,4. Поэтому для СВ X, по сравнению с СВ Y, изменяются только вероятности значений 2 и 3. В силу того, что пятый эксперт даёт мнение не зависимо от первых четырёх, имеем: , если его мнение отрицательно что происходит с вероятностью 0,4. Поэтому для СВ X, по сравнению с СВ Y, изменяются только вероятности значений 2 и 3. В силу того, что пятый эксперт даёт мнение не зависимо от первых четырёх, имеем: 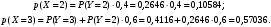 Тогда ряд распределений СВ X имеет вид:
Числовые характеристики случайной величины X найдём по определению. Математическое ожидание: 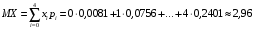 . .Дисперсия: 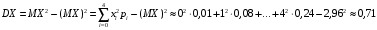 Среднее квадратическое отклонение (с.к.о.): Среднее квадратическое отклонение (с.к.о.): 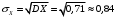 . .Очевидно, что предложение сотрудника получит положительную оценку, если 3 или 4 эксперта дадут предложению такую оценку. Тогда, если событие A – «предложение одобрено», то 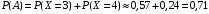 . . Пример 2.2. (Функция распределения СВ, плотность распределения и числовые характеристики непрерывной СВ, равномерное распределение). Поезда в метро ходят точно через 3 минуты (время между отправлениями двух соседних поездов). Пассажир приходит в метро в произвольный момент времени и садится в ближайший поезд, если он не переполнен, что бывает в 60% случаев. Если ближайший поезд переполнен, то пассажир дожидается следующего поезда и садится в него в любом случае. Построить функцию распределения времени (в минутах) от прихода пассажира на станцию до его отъезда (будем называть это время временем ожидания поезда). Найти плотность распределения и числовые характеристики (мат. ожидание, дисперсию и с.к.о.) времени ожидания поезда. Найти вероятность того, что это время будет более двух минут, но менее пяти минут. Решение. Пусть непрерывная случайная величина T – время (в минутах) ожидания поезда в метро. Построим функцию распределения 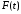 СВ T. По определению функции распределения для любого СВ T. По определению функции распределения для любого 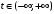 : :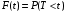 . .Функция распределения любой СВ определена на всей числовой прямой. Для непрерывной СВ функция распределения непрерывна на всей числовой прямой. Очевидно, что по условию задачи время ожидания поезда в метро не может быть меньше нуля минут и не может быть больше 6 минут. Тогда, если 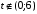 , то , то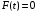 . Значение, которое принимает СВ T зависит от того, в какой момент пассажир придёт в метро (точнее, за сколько минут до отправления ближайшего поезда), а также от того, сядет ли он в ближайший или в следующий поезд. Чтобы найти . Значение, которое принимает СВ T зависит от того, в какой момент пассажир придёт в метро (точнее, за сколько минут до отправления ближайшего поезда), а также от того, сядет ли он в ближайший или в следующий поезд. Чтобы найти 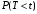 , при , при 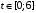 сделаем 2 гипотезы: сделаем 2 гипотезы: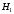 - «пассажир садится в ближайший поезд»; - «пассажир садится в ближайший поезд»;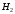 - «пассажир пропускает ближайший поезд и садится в следующий». - «пассажир пропускает ближайший поезд и садится в следующий».По условию 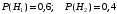 . Поскольку поезда отходят точно через 3 минуты, а пассажир приходит в метро в случайный момент времени, то, если имеет место гипотеза . Поскольку поезда отходят точно через 3 минуты, а пассажир приходит в метро в случайный момент времени, то, если имеет место гипотеза 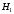 , то время ожидания поезда равномерно распределено на интервале , то время ожидания поезда равномерно распределено на интервале 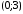 , т.е. при возрастании , т.е. при возрастании 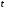 от 0 до 3 значение функции распределения линейно растёт от 0 до 1. Тогда от 0 до 3 значение функции распределения линейно растёт от 0 до 1. Тогда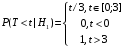 . .Аналогично, если имеет место гипотеза 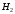 , то время ожидания поезда равномерно распределено на интервале , то время ожидания поезда равномерно распределено на интервале 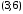 , таким образом: , таким образом: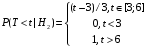 . .По формуле полной вероятности имеем: 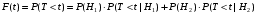 . .С учётом всех предыдущих равенств: 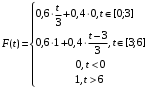 . . Таким образом функция распределения случайной величины T имеет вид: 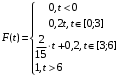 . .Плотность распределения СВ – это производная функции распределения, тогда для СВ T: 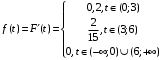 . .Таким образом, плотность распределения является кусочно-постоянной функцией, в точках 0; 3 и 6 плотность распределения не определена. Найдём числовые характеристики СВ T: Математическое ожидание: 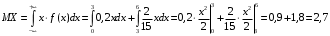 . .Дисперсия: 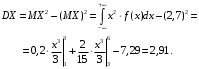 С.к.о.: 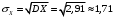 . .Вероятность попадания непрерывной СВ на некоторый интервал можно найти как интеграл от плотности распределения этой СВ по данному интервалу: 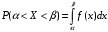 , ,однако в данном случае известна функция распределения, поэтому искомую вероятность можно найти проще: 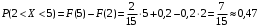 . .Пример 2.3. (Использование стандартных распределений при решении экономических задач, простейший поток событий, распределение Пуассона, показательное распределение). К киоску покупатели в среднем подходят через 30 секунд. Считая поток покупателей простейшим, найти вероятность того, что за три минуты к киоску подойдет: а) менее 3 покупателей; б) хотя бы два покупателя. Найти математическое ожидание и среднеквадратическое отклонение числа покупателей за три минуты. Найти плотность распределения и числовые характеристики времени между двумя соседними покупателями и вероятность того, что это время составит от одной до двух минут. Найти вероятность того, что, если продавец покинет рабочее место на 3 минуты, то за это время к киоску не подойдёт ни одного покупателя. Решение. Пусть случайная величина 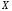 - число покупателей, подходящих к киоску за 3 минуты. Поскольку поток покупателей является простейшим, то - число покупателей, подходящих к киоску за 3 минуты. Поскольку поток покупателей является простейшим, то 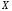 представляет собой число событий в простейшем потоке в течение заданного промежутка времени. Такая СВ имеет распределение Пуассона с параметром представляет собой число событий в простейшем потоке в течение заданного промежутка времени. Такая СВ имеет распределение Пуассона с параметром 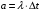 , где , где 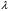 - интенсивность потока, - интенсивность потока, 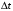 - величина заданного промежутка времени. Интенсивность потока – это среднее число событий в потоке за единицу времени. По условию задачи, - величина заданного промежутка времени. Интенсивность потока – это среднее число событий в потоке за единицу времени. По условию задачи, 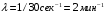 , , 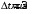 , а, значит, параметр распределения Пуассона , а, значит, параметр распределения Пуассона 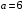 , и вероятности могут быть найдены с помощью формулы Пуассона: , и вероятности могут быть найдены с помощью формулы Пуассона: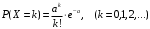 , где , где 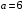 . . Искомые вероятности равны: 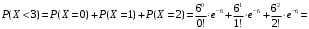 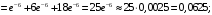 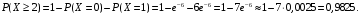 Для нахождения числовых характеристик распределения Пуассона воспользуемся известными формулами: 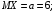 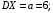 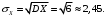 Пусть теперь T – время (в минутах) между соседними покупателями. Поскольку поток покупателей является простейшим, то такая СВ имеет показательное распределение с параметром 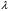 , равным интенсивности потока. Учтём, что , равным интенсивности потока. Учтём, что 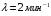 и воспользуемся формулой плотности показательного распределения. Тогда плотность распределения СВ T имеет вид: и воспользуемся формулой плотности показательного распределения. Тогда плотность распределения СВ T имеет вид: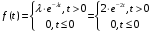 . .Числовые характеристики (мат. ожидание, дисперсия, с.к.о.): 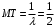 (мин); (мин); 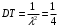 (мин2); (мин2); 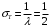 (мин). (мин).Для показательного распределения можно воспользоваться формулой попадания СВ на заданный интервал: если 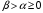 , то , то 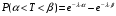 , тогда , тогда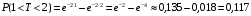 . .Заметим, что событие «если продавец покинет рабочее место на 3 минуты, то за это время к киоску не подойдёт ни одного покупателя», которое мы обозначим буквой A, в силу отсутствия последействия в простейшем потоке, может быть выражено, как через СВ X, так и через СВ T, а именно « 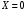 » или « » или «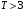 ». Тогда ». Тогда 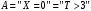 , соответственно, вероятность события A может быть найдена двумя способами: , соответственно, вероятность события A может быть найдена двумя способами: 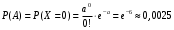 или или 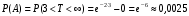 . .Пример 2.4. (Предельны теоремы теории вероятностей, нормальное распределение). Exit poll (опрос на выходе с избирательных участков), проводимый по репрезентативной выборке среди 1000 независимых избирателей, показал, что 530 человек проголосовали за некоторого кандидата. В выборах участвует миллион избирателей. Построить функцию плотности распределения процента избирателей, которые проголосуют за данного кандидата. Найти вероятность того, что данный кандидат не выиграет данные выборы. Построить интервал, в который попадёт процент проголосовавших за данного кандидата с вероятностью 0,99. Решение. Пусть X – число избирателей, голосующих за данного кандидата среди всех (т.е. миллиона) избирателей. Поскольку значение этой СВ зависит от очень большого числа причин, среди которых нет доминирующей причины (т.е. от голоса каждого из миллиона избирателей), то, согласно центральной предельной теореме, случайная величина X имеет нормальное распределение. Поскольку exit poll проводился по репрезентативной выборке (т.е. выборке большого объёма, представляющей все группы избирателей в необходимых пропорциях), то вероятность того, что случайно выбранный избиратель проголосует за данного кандидата можно найти по теореме Бернулли, которая является одной из форм закона больших чисел, 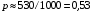 , математическое ожидание и дисперсия определяются из соответствующих формул для биномиального распределения: , математическое ожидание и дисперсия определяются из соответствующих формул для биномиального распределения: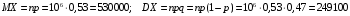 , ,тогда с.к.о.: 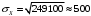 , т.е. , т.е. 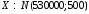 . .Пусть теперь Y - процент избирателей, которые проголосуют за данного кандидата, тогда 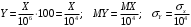 , причём СВ Y также имеет нормальное распределение, т.е. , причём СВ Y также имеет нормальное распределение, т.е. 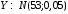 . Тогда искомая плотность распределения СВ Y имеет вид: . Тогда искомая плотность распределения СВ Y имеет вид: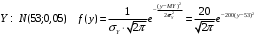 . .Вероятность того, что кандидат проиграет, можно найти, используя формулу вероятности попадания нормально распределённой СВ на заданный интервал: если 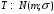 , то: , то: 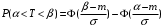 , ,где 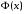 - функция Лапласа, которая является табличной функцией. Тогда для СВ Y имеем: - функция Лапласа, которая является табличной функцией. Тогда для СВ Y имеем: 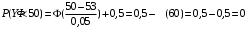 с очень высокой степенью точности. Заметим, что искомое значение могло быть найдено также с помощью интегральной теоремы Муавра-Лапласа: с очень высокой степенью точности. Заметим, что искомое значение могло быть найдено также с помощью интегральной теоремы Муавра-Лапласа: 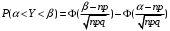 , ,которая, конечно, даёт такой же результат, поскольку представляет собой объединение приведённых выше рассуждений в одну формулу. Чтобы построить интервал, в который попадает значение СВ Y с заданной вероятностью, воспользуемся ещё одной формулой, справедливой для нормального распределения. Если 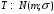 , то , то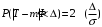 . .Тогда 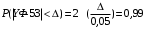 . Тогда, . Тогда, 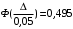 . Из таблиц функции Лапласа: . Из таблиц функции Лапласа: 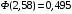 , откуда , откуда 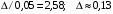 . Искомый интервал, в который процент проголосовавших за кандидата попадает с вероятностью 0,99, имеет вид . Искомый интервал, в который процент проголосовавших за кандидата попадает с вероятностью 0,99, имеет вид 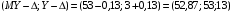 . Таким образом, при большом числе избирателей и наличии репрезентативной выборки exit poll даёт результаты выборов с высокой степенью точности. . Таким образом, при большом числе избирателей и наличии репрезентативной выборки exit poll даёт результаты выборов с высокой степенью точности.Задачи для самостоятельного решения 1. Процесс выполнения заказа на изготовление изделия состоит из изготовления двух групп комплектующих на двух различных предприятиях, работающих независимо, и сборки изделия на третьем заводе, которую можно начинать после того, как будут получены комплектующие с обоих заводов. Срок выполнения заказа 6 суток. Дискретные случайные величина 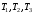 - время (в сутках) выполнения работ (вместе с доставкой готовых изделий) на каждом из предприятий. Известны ряды распределений этих СВ: - время (в сутках) выполнения работ (вместе с доставкой готовых изделий) на каждом из предприятий. Известны ряды распределений этих СВ:
Пусть T – общее время выполнения заказа. Построить ряд распределений СВ T, найти числовые характеристики (м.о., дисперсию, с.к.о). Найти вероятность того, что заказ будет выполнен в срок. 2. Телефон с «автодозвоном» формирует автоматический звонок, причем каждый последующий звонок производится в том случае, если предыдущий звонок не принят. Вероятность того, что абонент примет вызов, равна 0,4. Построить закон распределения и найти числовые характеристики числа звонков, если число звонков не ограничено. Найти вероятность того, что будет сделано не более 5 звонков. 3. Непрерывная СВ 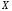 задана функцией плотности распределения: задана функцией плотности распределения: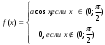 . .Найти значение параметра  , числовые характеристики СВ , числовые характеристики СВ 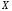 и вероятности событий: и вероятности событий: 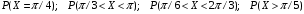 . . 4. На телефон доверия звонки приходят в среднем через 4 минуты. Считая поток звонков простейшим, построить ряд распределения числа звонков за 10 минут, найти вероятность того, что за 10 минут на телефон придет не менее 2-х звонков. Построить плотность распределения и функцию распределения времени между двумя соседними звонками, найти вероятность того, что это время составит от 3 до 5 минут. 5. Опрос, производимый у выхода с избирательного участка показал, что среди 500 опрошенных 150 проголосовали за некоторого кандидата. Найти вероятность того, что а) среди 200 случайно выбранных избирателей ровно 65 проголосовали за этого кандидата; б) среди этих 200 избирателей за кандидата проголосовали не менее 32%. Считая процент проголосовавших за данного кандидата среди всех избирателей, число которых велико, непрерывной СВ, построить функцию плотности распределения этой СВ и найти числовые характеристики. |