Теоритико вероятноостные основы. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЕ_ОСНОВЫ_анализа(1). Учебное пособие Теоретиковероятностные основы комплексного анализа социальноэкономических систем. Типовые задачи продвинутого уровня
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
ПРЕДИСЛОВИЕ Учебное пособие «Теоретико-вероятностные основы комплексного анализа социально-экономических систем. Типовые задачи продвинутого уровня» предназначено для подготовки студентов, обучающихся по направлениям «Бизнес-информатика», «Прикладная информатика», которые изучают расширенный курс дисциплины «Теория вероятностей и математическая статистика». Оно будет полезно студентам бакалавриата и магистратуры экономических профилей подготовки для формирования компетенций, направленных на приобретение навыков анализа и управления социально-экономическими процессами с учётом их случайного характера. Социально-экономическая система представляет собой совокупность экономических субъектов, взаимосвязанных и взаимодействующих между собой в сфере производства и потребления, обмена и распределения. Взаимодействие экономических субъектов внутри системы всегда обусловлено большим числом внешних факторов, имеющих значительную степень неопределённости. Поэтому анализ и управление социально-экономическими системами требует учёта стохастического характера процессов, протекающих в таких системах. В настоящем пособии на конкретных примерах показано, как в экономических системах производится математическое описание процессов, имеющих значительную степень неопределённости, как происходит анализ этих процессов и управление ими. Решение задач, представленных в пособии, требует наличия базовых знаний теории вероятностей. Пособие направлено на формирование навыков их использования в экономических задачах и расширение возможностей экономического анализа при изучении продвинутых курсов теории вероятностей и математической статистики. Представленные задачи сопровождаются подробными решениями с объяснениями всех необходимых деталей и ссылками на используемые теоретические положения теории вероятностей. 1. Алгебра событий как основа анализа стохастического характера социально-экономических процессов Пример 1.1 (Классическая схема анализа случайных явлений, формула урновой схемы). В отделе предприятия 10 сотрудников, среди которых 3 инженера. Для проведения некоторых работ случайно выбирается 3 сотрудника. Найти вероятности того, что среди выбранных сотрудников нет инженеров и того, что среди них инженеры составляют большинство. Решение. Введём обозначения для событий: A – «среди выбранных нет инженеров»; B – «среди выбранных инженеры составляют большинство». Найдём вероятность события А.Для решения задачи воспользуемся классической формулой вычисления вероятностей. Опыт – выбор сотрудников. Элементарный исход – это список из трёх выбранных сотрудников. Поскольку выбор осуществляется случайно, то все исходы равновозможны. Следовательно, применима классическая формула вычисления вероятностей: 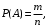 где  - общее число элементарных исходов опыта; - общее число элементарных исходов опыта; 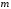 - число исходов благоприятных событию A. Опыт представляет собой случайный выбор по схеме без повторений, причём порядок выбора сотрудников не важен. Поэтому классическую формулу можно применить в виде формулы урновой схемы. Учтём, что всего из 10 сотрудников надо выбрать трёх, при этом из 3-х инженеров не выбирается никто, а из 7 оставшихся выбирается 3 человека. Тогда по формуле урновой схемы имеем: - число исходов благоприятных событию A. Опыт представляет собой случайный выбор по схеме без повторений, причём порядок выбора сотрудников не важен. Поэтому классическую формулу можно применить в виде формулы урновой схемы. Учтём, что всего из 10 сотрудников надо выбрать трёх, при этом из 3-х инженеров не выбирается никто, а из 7 оставшихся выбирается 3 человека. Тогда по формуле урновой схемы имеем: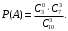 Найдём численные значения для чисел сочетаний, входящих в формулу: 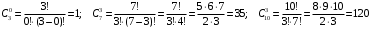 Окончательно имеем: 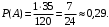 Теперь найдём вероятность события B. Очевидно, что для того, чтобы инженеры составляли большинство, среди выбранных их должно быть 2 или 3. Поэтому введём 2 события: 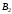 - «среди выбранных ровно 2 инженера» и - «среди выбранных ровно 2 инженера» и 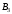 - «среди выбранных ровно 3 инженера». Тогда событие B является суммой этих событий. Напомним, что суммой событий называется событие, состоящее в том, что произошло хотя бы одно из слагаемых событий. Таким образом, - «среди выбранных ровно 3 инженера». Тогда событие B является суммой этих событий. Напомним, что суммой событий называется событие, состоящее в том, что произошло хотя бы одно из слагаемых событий. Таким образом, 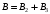 . .Заметим, что события 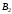 и и 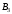 являются несовместными, поэтому применима теорема сложения вероятностей для несовместных событий: являются несовместными, поэтому применима теорема сложения вероятностей для несовместных событий: 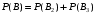 . .Осталось заметить, что вероятности событий 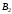 и и 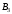 могут быть найдены по формуле урновой схемы, аналогично вероятности события A: могут быть найдены по формуле урновой схемы, аналогично вероятности события A: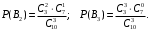 Тогда 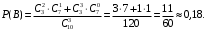 Пример 1.2 (Теоремы теории вероятностей, многовариантность составления моделей случайных явлений). Руководство некоторого района проводит комплексную проверку производственной и финансовой дисциплины предприятий. В районе 10 предприятий, среди которых 2 предприятия имеют скрытые нарушения производственной дисциплины и 3 предприятия, имеющие нарушения финансовой дисциплины, предприятий, имеющих нарушения обоих типов, нет. Руководство района случайно выбирает 8 предприятий для проверки. Проверка поручается двум комиссиям (по 4 предприятия каждому). Первая комиссия проводит проверку производственной дисциплины, вторая – финансовой. Найти вероятности событий: A – «все нарушения будут обнаружены»; B –«будет обнаружено хотя бы 1 нарушение»; C – «ни одного нарушения не будет обнаружено». Решение. При решении задачи продемонстрируем возможность использования различных подходов к перечислению исходов опыта и, соответственно, разных способов вычисления вероятностей. Вероятность события A, найдём, рассматривая случайный выбор проверяемых предприятий с учётом порядка выбора.Занумеруем предприятия числами от 1 до 10, причём первые 2 номера присвоим предприятиям, имеющим производственные нарушения, а следующие 3 номера – имеющим финансовые нарушения. Теперь опыт представляет собой случайный выбор 8 чисел из первых 10 натуральных. Будем считать, что первые 4 числа – это номера предприятий, проверка которых проводит первая комиссия, следующие 4 – вторая комиссия. При таком подходе к перечислению исходов опыта важен порядок выбора чисел, элементарным исходом является упорядоченный набор из 8 чисел, а общее число элементарных исходов вычисляется с использованием числа размещений: 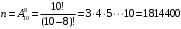 . .Поскольку выбор предприятий производится случайно, то все исходы равновозможны, и применима классическая формула вычисления вероятностей. Для события A у всех благоприятных исходов среди первых 4-х чисел набора есть числа 1 и 2, а среди последних 4-х есть числа 3, 4 и 5. Таким образом, сначала производится выбор двух мест (для чисел 1 и 2) из первых четырёх, затем производится выбор трёх мест (для чисел 3, 4 и 5) из последних четырёх, а затем на 3 оставшихся места произвольно выбираются числа из оставшихся пяти чисел (от 6 до 10). Порядок выбора всё время надо учитывать, поскольку он учитывался при подсчёте общего числа исходов. Тогда число благо приятных исходов события A посчитывается так: 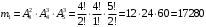 . .В дальнейшем в пособии уже не будет столь подробных пояснений того, как производятся вычисления по формулам комбинаторики. Теперь по классической формуле: 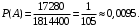 Заметим, что событие B является противоположным к событию C. Поэтому сначала найдём вероятность события C. Применим метод, часто используемый в комбинаторных задачах для облегчения рассуждений. Будем считать, что из 10 выбирается не 8 чисел, а все 10 с учётом порядка выбора. Будем считать, что первые 4 выбранных предприятия проверяются первой комиссией, следующие 4 – второй комиссией, последние же 2 предприятия не проверяются вовсе. Введём 2 события и представим событие C как их произведение: 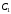 - «среди первых 4-х выбранных чисел нет чисел 1 и 2»; - «среди первых 4-х выбранных чисел нет чисел 1 и 2»;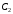 - «среди следующих 4-х выбранных чисел нет чисел 3, 4 и 5». Напомним, что произведение событий – это событие, состоящее в том, что произошли все события – сомножители. Тогда - «среди следующих 4-х выбранных чисел нет чисел 3, 4 и 5». Напомним, что произведение событий – это событие, состоящее в том, что произошли все события – сомножители. Тогда 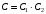 . Поскольку события . Поскольку события 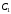 и и 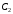 зависимы, то применим теорему умножения вероятностей для произвольных событий: зависимы, то применим теорему умножения вероятностей для произвольных событий: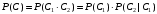 , ,где 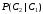 - условная вероятность события - условная вероятность события 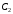 , при условии, что событие , при условии, что событие 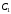 произошло. При нахождении вероятности события произошло. При нахождении вероятности события 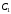 будем рассматривать только случайный выбор 4-х чисел на места с 1 по 4, не рассматривая выбор чисел на остальные места. Элементарным исходом теперь является неупорядоченный набор из 4-х чисел, случайно выбранных из первых 10 натуральных чисел. Это позволяет не учитывать порядок выбора и использовать формулу урновой схемы: будем рассматривать только случайный выбор 4-х чисел на места с 1 по 4, не рассматривая выбор чисел на остальные места. Элементарным исходом теперь является неупорядоченный набор из 4-х чисел, случайно выбранных из первых 10 натуральных чисел. Это позволяет не учитывать порядок выбора и использовать формулу урновой схемы: 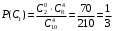 . .Для нахождения условной вероятности используем формулу полной вероятности. Сформулируем систему гипотез: 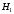 - «числа 1 и 2 находятся в упорядоченном наборе выбранных чисел на местах с 5 по 8»; - «числа 1 и 2 находятся в упорядоченном наборе выбранных чисел на местах с 5 по 8»;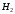 - «одно из 2-х чисел 1 и 2 находится на местах с 5 по 8, а другое на местах 9 или 10» - «одно из 2-х чисел 1 и 2 находится на местах с 5 по 8, а другое на местах 9 или 10»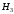 - «числа 1 и 2 находятся на 9 и 10 местах». - «числа 1 и 2 находятся на 9 и 10 местах».Заметим, что при условии 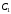 эти 3 события составляют полную группу попарно несовместных событий, т.е. при любом выборе чисел ровно одно из этих трёх событий всегда будет происходить. Формула полной вероятности в этом случае имеет вид: эти 3 события составляют полную группу попарно несовместных событий, т.е. при любом выборе чисел ровно одно из этих трёх событий всегда будет происходить. Формула полной вероятности в этом случае имеет вид: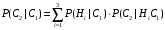 . .Учтём, что 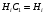 при при 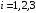 . Тогда эта формула примет вид: . Тогда эта формула примет вид: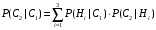 . .При нахождении вероятности гипотезы 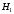 будем рассматривать только случайный выбор 4-х чисел на места с 5 по 8, не рассматривая выбор чисел на остальные места. Это позволяет не учитывать порядок выбора и использовать формулу урновой схемы. Тогда: будем рассматривать только случайный выбор 4-х чисел на места с 5 по 8, не рассматривая выбор чисел на остальные места. Это позволяет не учитывать порядок выбора и использовать формулу урновой схемы. Тогда: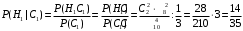 . .Аналогично: 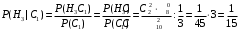 . . Тогда 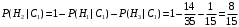 . .Теперь найдём условные вероятности события 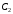 . Как и раньше, учтём, что . Как и раньше, учтём, что 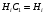 при при 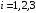 . Каждый раз воспользуемся формулой урновой схемы, учитывая, сколько мест с 5 по 8 уже занято числами 1 и 2: . Каждый раз воспользуемся формулой урновой схемы, учитывая, сколько мест с 5 по 8 уже занято числами 1 и 2: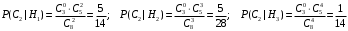 . .Тогда по формуле полной вероятности: 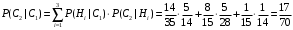 . .Теперь 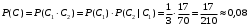 . .Наконец, 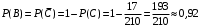 . .Пример 1.3 (Формула Байеса, байесовский подход к принятию решений). В некоторой кредитной организации для одобрения кредита или отказа в его выдаче принята следующая процедура проверки клиента на платежеспособность, т.е. способность клиента вернуть кредит в установленный срок. На первом этапе проверяется кредитная история клиента. Если после этого решение не принято, то на втором этапе проводится проверка сведений о нынешнем месте работы (или её отсутствии). После первого или второго этапа принимается решение о выдаче кредита, если вероятность платежеспособности клиента составляет не менее 80%, решение об отказе в выдаче кредита принимается, если эта вероятность составляет не более 20%. Если и после второго этапа решение не принято, то клиенту предлагается предоставить поручительство со стороны лиц, удовлетворяющих определённым критериям, или предоставить имущественный залог, или выполнить оба варианта. После третьего этапа принимается решение о выдаче кредита, если вероятность возврата составляет не менее 70%, в противном случае принимается решение об отказе. Кредитные службы банка обладают следующей статистической информацией: - среди лиц, подающих заявление о выдаче кредита, платежеспособными являются 60%; - среди платежеспособных клиентов никогда не брали кредитов 30%, имеют безукоризненную кредитную историю 60%, имеют недостатки в кредитной истории 10%; среди неплатежеспособных аналогичные данные составляют 20%, 30% и 50%; - среди платежеспособных клиентов работали более трёх лет на нынешнем месте работы и имеют необходимый установленный годовой доход 60% клиентов, проработали от года до трёх при наличии необходимого дохода 30%, не имеют работы или проработали менее года 10% клиентов; для неплатёжеспособных клиентов эти числа составляют 20%, 40% и 40% соответственно; - среди платежеспособных клиентов по требованию банка предоставляют поручительство и имущественный залог 50% клиентов, предоставляют только поручительство 20%, только залог – 20%, не предоставляют ничего 10% клиентов; для неплатёжеспособных клиентов эти числа составляют 15%, 10%, 30% и 45% соответственно. Клиент I никогда не брал кредитов, работает 7 лет на последнем месте работы, имея необходимый годовой доход, предоставлять поручительство или залог изначально отказался. Клиент II имеет недостатки в кредитной истории, работает три с половиной года на последнем месте работы, имея необходимый доход, и способен предоставить имущественный залог, но поручителей не имеет. Какие решения о выдаче кредита (или отказе) будут приняты по клиентам I и II? Решение. Процедура выработки решения представляет собой байесовский подход к принятию решений, который, как считают многие, имеет место при любом процессе принятия решений. Рассмотрим процесс принятия решения по заявлению клиента I. Сделаем 2 гипотезы: 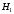 - «клиент платежеспособен»; - «клиент платежеспособен»; 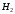 - «клиент неплатежеспособен». Все вероятности определяются из статистических данных. - «клиент неплатежеспособен». Все вероятности определяются из статистических данных. Априорные (т.е. изначальные) вероятности гипотез составляют: 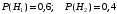 . Эти вероятности не позволяют принять решения о выдаче или невыдаче кредита. . Эти вероятности не позволяют принять решения о выдаче или невыдаче кредита. Первый этап байесовского процесса. Рассмотрим событие A – «клиент никогда не брал кредитов», которое имеет место для клиента I. По формуле Байеса найдём апостериорные (т.е. «после опыта») вероятности гипотез. Из статистических данных имеем: 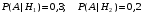 . Тогда по формуле Байеса: . Тогда по формуле Байеса: 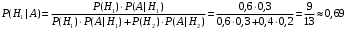 . .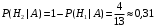 . .Эти вероятности по условию не позволяют принять решение по кредиту. Переходим ко второму этапу байесовского процесса. Вновь полученные вероятности принимаются теперь за априорные вероятности гипотез: 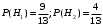 . .Для клиента I имеет место событие B – «клиент работает более трёх лет, имея необходимый доход». Проведём аналогичные расчёты по формуле Байеса: 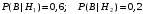 . .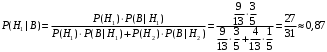 . .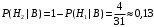 . .Эти вероятности позволяют принять решение. Кредит клиенту I будет одобрен. Теперь аналогично рассмотрим процесс принятия решения по заявлению клиента II. Первый этап. 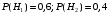 . A – «клиент имеет недостатки в кредитной истории». . A – «клиент имеет недостатки в кредитной истории». 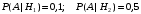 . .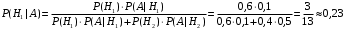 . .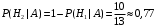 . .Эти вероятности не позволяют принять решение по кредиту. Второй этап. 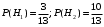 . Событие B – «клиент работает более трёх лет, имея необходимый доход». . Событие B – «клиент работает более трёх лет, имея необходимый доход». 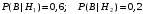 . .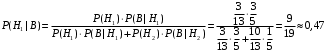 . .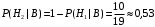 . .Эти вероятности вновь не позволяют принять решение по кредиту. Третий этап. 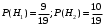 . Событие C – «клиент способен предоставить имущественный залог, но поручителей не имеет». . Событие C – «клиент способен предоставить имущественный залог, но поручителей не имеет». 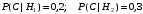 . .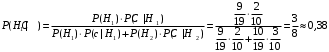 . .По условиям третьего этапа клиенту будет отказано в выдаче кредита. Задачи для самостоятельного решения 1. Руководство некоторого района проводит комплексную проверку производственной и финансовой дисциплины предприятий. В районе 10 предприятий, среди которых 2 предприятия имеют скрытые нарушения производственной дисциплины и 2 предприятия, имеющих по 1 скрытому нарушению финансовой дисциплины, при этом 1 предприятие имеет нарушения обоих типов (по 1 нарушению каждого типа). Руководство района выделяет 4-х инспекторов для проверки производственной дисциплины и 4-х инспекторов для проверки финансовой дисциплины. Каждый из 8 инспекторов случайно, не зависимо от других инспекторов, выбирает себе 4 предприятия для проверки. Проверка одного и того же предприятия несколькими инспекторами одновременно вполне возможна. Все инспекторы обнаруживают при проверке имеющиеся нарушения с вероятностью 0,7. Найдите вероятности событий: A – «все нарушения будут обнаружены»; B –«будет обнаружено хотя бы 1 нарушение»; C – «ни одного нарушения не будет обнаружено»; D – «будет обнаружено более половины нарушений». 2. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в любом из автоматов закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найти вероятность того, что к концу дня кофе останется в обоих автоматах. 3. Вероятность выигрыша лотерейного билета 0,01. Найти минимальное количество таких билетов, которое нужно прибрести, чтобы с вероятностью 0,99 среди них был хотя бы один выигрышный если общее число билетов очень велико. 4. Из разрезной русской азбуки (33 буквы) случайно и последовательно выбирается 5 букв, из которых в порядке выбора выкладывается «слово». Найти вероятности событий: A – «получилось слово АВТОР»; B – « получилось слово БАРАН»; C – «первая буква в слове - О»; D - «четвёртая буква в слове - О»; E – «в слове есть буква О»; F – «в слове ровно 2 гласных»; G – «в слове ровно 3 согласных»; H – «в слове 2 гласных и 3 согласных»; K – «в слове есть буквы А,В,Т,О,Р»; L – « в слове есть буквы А,В,Т,О,Р, и «слово» есть в большом орфографическом словаре русского языка». 5. а) В условиях примера 1.3 определить, какие решения будут приняты для клиентов, III и IV, если клиент III имеет безукоризненную кредитную историю, в настоящий момент является безработным, может предоставить поручительство, но не имеет залога; клиент IV имеет недостатки в кредитной истории, работает в течение двух лет на последнем месте работы, имея необходимый доход, и готов при необходимости предоставить, как поручительство, так и залог. б) В условиях примера 1.3 первый и второй этапы процедуры проверки клиентов меняются местами. В остальном условия остаются прежними. Определить, какие решения о выдаче (или невыдаче) кредита будут приняты банком по клиентам I, II, III и IV? |
