Учёт влияния тропосферы. Учет влияние троросферы 39276 (1). Учёт влияния тропосферы на результаты спутниковых измерений
 Скачать 375.26 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОДЕЗИИ И КАРТОГРАФИИ Факультет дистанционных форм обучения Заочное отделение Реферат По дисциплине: «Высокоточные спутниковые системы в прикладной геодезии» На тему: «Учёт влияния тропосферы на результаты спутниковых измерений» Выполнила студентка 6 курса заочного отделения ФДФО Специальность Прикладная геодезия Горланова Наталья Сергеевна Москва 2020 Введение Скорость распространения сигналов представляет особую важность для любой дальномерной системы. Именно скорость, умноженная на измеренный интервал времени распространения, обеспечивает меру дальности. Сигналы, передаваемые спутниками GPS/ГЛОНАСС, на их пути к приемнику, расположенному на Земле или около поверхности, вынуждены проходить через земную атмосферу. В результате взаимодействия сигналов с составными заряженными частицами и нейтральными атомами и молекулами атмосферы, их скорость и направление распространения изменяются. Наиболее характерными областями распространения является тропосфера, тропопауза, стратосфера и ионосфера. Объединенное влияние нейтральной атмосферы, состоящей из тропосферы, тропопаузы и стратосферы называется тропосферной рефракцией. Действие тропосферной рефракции происходит до высот примерно 40 км от поверхности Земли. Для частот ниже 30 ГГц тропосфера ведет себя как недиспергирующая (нерассеивающая) среда, то есть рефракция не зависит от частоты сигнала, передаваемого через нее 1. Влияние тропосферы на параметры наблюдений Нейтральная атмосфера (тропосфера, тропопауза и стратосфера) является недиспергирующей средой. О ее влиянии говорят как о тропосферной рефракции, которая не зависит от частоты и, следовательно, влияет и на кодовую модуляцию, и на фазу несущей одинаковым образом. Влияние представляет задержку (с тем же знаком, что у ионосферы для кодов), которая достигает 2.0-2.5 м в зенитном направлении и увеличивается примерно пропорционально косекансу угла высоты, достигая 20-28 м на высоте 5°. Измеренные дальности оказываются длинней, чем геометрическое расстояние между приемником и спутником. Задержка зависит от температуры, влажности и давления, изменяется с высотой пользователя и с типом местности под траекторией сигнала. Из-за того, что тропосферная рефракция не зависит от частоты несущей, ее невозможно устранять в двухчастотных наблюдениях, в отличие от ионосферной рефракции. Показатель преломления N удобно определять через индекс показателя преломления n, как  . По аналогии с выражениями для ионосферной рефракции тропосферную задержку можно представить, как: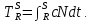 Показатель преломления воздуха для электромагнитных волн, используемых в спутниковых системах определения местоположения, зависит от состояния атмосферы, то есть от температуры воздуха T, давления P, и влажности (давления водяных паров) e: 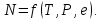 Показатель преломления является функцией положения точек пространства, через которые проходит путь сигнала, так как метеорологическое поле атмосферы считается регулярным лишь условно. Оно является неоднородным, особенно вблизи поверхности земли. Поэтому, для вычисления пути, пройденного сигналом спутника и найденного из прямых или косвенных определений, необходимо знать действительный показатель преломления воздуха вдоль пути. Действительный средний показатель преломления n теоретически определяется выражением: 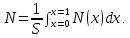 Это равенство предполагает, что функция N(x) от пути x известна. Она может быть определена только при достоверных предположениях о строении атмосферы или из непосредственных измерений. 2.Математические модели атмосферных задержек Атмосфера изменяет скорость (величину и направление) распространения радиосигналов. Это явление называется рефракцией. Изменение в скорости распространения изменяет время прохождения сигнала, которое является основой измерений в ГНСС. Рассмотрим кратко варианты математического определения задержек для различных слоев атмосферы. Рефракция сигналов ГНСС в атмосфере Земли приводит к изменениям в скорости и в направлении сигнала.  Рисунок 1 – Рефракция сигналов ГНСС в атмосфере Земли приводит к изменениям в скорости и в направлении сигнала. 2.1 Модели тропосферной задержки Модель показателей преломления и тропосферной задержки Хопфилд. Модель Хопфилд (Helen S. Hopfield) основана на соотношениях между показателями преломления на высоте h и у земной поверхности. Эти соотношения были выведены эмпирически по большому объему измерений. Полученную модель называют моделью с профилем показателя преломления четвертого порядка:  где h – высота над антенной,  – сухой показатель преломления на поверхности, а 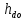 – (=43 км) определяет высоту над антенной, на которой показатель преломления равен нулю  .Модель Хопфилд для влажного показателя преломления подобна:  где  – влажный показатель преломления на поверхности, и  = 12 км.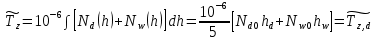 + 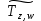.Выражения для сухого и влажного показателей преломления: 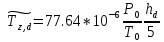 , .Значения  составляют 2.3-2.6 м на уровне моря и становятся меньше с увеличением высоты: около 2 м на высоте около 1.5 км и около 1 м на вершинах пиков в Гималаях. Соответствующая влажная задержка зависит от распределения паров воды вдоль пути сигнала и может быть очень переменной. Модели влажной задержки , основанные на метеорологических данных для поверхности Земли, обычно менее точны, их типичная ошибка 1-2 см. Использование средних метеорологических условий, а не действительных измерений, вводит дополнительные ошибки моделирования и в сухую, и во влажную задержку, и ошибка в полной зенитной задержке может быть 5-10 см.Для перехода от направления в зенит к высоте E у Хопфилд вводятся сухая и влажная функции отображения:  , 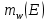= 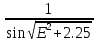.В итоге полная тропосферная задержка для высоты Е получается по формуле: 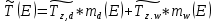 Хопфилд разработала несколько моделей тропосферной задержки, которые отличаются способами интегрирования профилей. Также, существует и другая модель учета тропосферной задержки – модель Саастамойнена. Она была разработана с использованием газовых законов и упрощающих предположений, касающихся изменений в давлении, температуре и влажности с высотой. 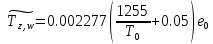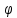Сухая и влажная зенитные задержки даются как:  , где  – температура (в Кельвинах),  – полное давление и – парциальное давление паров воды (оба в миллибарах), все определенные у местоположения антенны по измерениям или по модельным данным стандартной атмосферы,  - широта, а H –высота антенны над уровнем моря (км).Заключение Итак, в реферате были описаны модели тропосферы, используемые при спутниковых измерениях. Приводится информация о трёх распространённых моделях для расчёта зенитной задержки – биквадратная модель Хопфилд, модифицированная модель Хопфилд, модель Саастамойнена. На основании источников могу сделать вывод о том, что рассмотренные модели обеспечивают примерно одинаковый уровень точности. На сегодняшний день производятся новые исследования и предоставляются новые методы, так как Современные ГНСС постоянно развиваются, и модельный учёт тропосферы неизбежно станет сдерживающим фактором для дальнейшего развития системы Список используемой литературы 1. Клюшин Е. Б., Куприянов А. О., Шлапак В. В.;Спутниковые методы измерений в геодезии. (Часть 1). Учебное пособие. М.: Изд. МИИГАиК. УПП «Репрография», 2006 г. 2.Генике А. А., Побединский Г. Г.; Глобальные спутниковые системы определения местоположения и их применение в геодезии; Москва: ФГУП Картгеоцентр, 2004 г. 3.Большая советская энциклопедия: Тропосфера [Электронный ресурс] – http://www.worklib.ru/dic/Тропосфера/ 4.Антонович К. М.; Использование СРНС в геодезии. Том 1 / Антонович К. М., – Москва: ФГУП Картгеоцентр, 2005 г. 5.Хенриксен С., Манчини А., Човица Б.; Использование исскуственных спутников для геодезии; Москва: Издательство МИР, 1975 г. |