Учреждение образования
 Скачать 0.61 Mb.
|
|
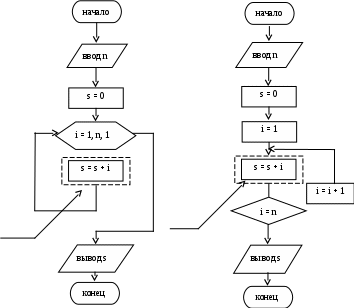
Тема: Решение задач, имеющих алгоритмы простейшей циклической структуры. Цель: Приобрести навыки математической формулировки содержательной постановки задачи, выбора метода, разработки алгоритма и программы её решения. При составлении алгоритмов решения задач возникает необходимость неоднократного повторения одних и тех же действий. Участок алгоритма, где многократно повторяются вычисления при различных значениях используемых в нём величин, называют циклом, а сам алгоритм, содержащий циклы, - циклическим. Циклические алгоритмы позволяют существенно сократить объём программы за счёт многократного выполнения группы повторяющихся вычислений. Специально изменяемый по заданному закону параметр, входящий в тело цикла, называется переменной цикла.Переменная цикла используется для подготовки очередного повторения цикла. Переменной цикла могут быть индексы массивов, аргументы вычисляемых функций и другие величины. Во время выполнения тела цикла параметры переменной цикла изменяются с заданным шагом. Следовательно, при организации циклических вычислений необходимо задать начальное значение переменной цикла, закон её изменения и предусмотреть проверку на окончание цикла, при выполнении которой произойдёт завершение цикла. Циклы, в теле которых нет разветвлений и других встроенных в них циклов, называют простыми.В противном случае их относят к сложным. Циклические алгоритмы разделяют надетерминированныеи итерационные. Циклы, в которых число повторений заранее известно из исходных данных или определено в ходе решения задачи, называют детерминированными.Для организации детерминированных циклов наиболее целесообразно использовать блок модификации, внутри которого указывается переменная цикла, её начальное и конечное значения, а также шаг её изменения (если шаг изменения равен 1, то его допускается не указывать). Организовать подобный цикл возможно и при использовании блока проверки условия вместо блока модификации, однако при этом несколько усложняется алгоритм и теряется его рациональность. Пример 2.1. Дано натуральное число n. Найти сумму первых n членов натурального ряда. Варианты схемы алгоритма циклической структуры решения задачи приведены на рис. 2.1. При этом в схеме на рис. 2.1,а цикл организован с использованием блока модификации, а на рис. 2.1,б – блока проверки условия. В обоих алгоритмах операция нахождения суммы, при предварительном обнулении значения переменной s (блок 3), повторяется n раз. В теле цикла использована операция присваивания s = s + i, по которой и осуществляется вычисление суммы путём прибавления к предыдущему значению переменной s всё новых значений переменной i. Цикл является детерминированным и количество его повторений заранее определено (n раз). В качестве переменной цикла i принято текущее значение членов натурального ряда. Использование алгоритма с блоком модификации предпочтительнее, так как он обладает лучшей наглядностью.
Циклы, в которых число повторений неизвестно из исходных данных и не определено по ходу решения задачи, называют итерационными.В итерационных циклах невозможно использовать блок модификации, так как  при организации таких циклов заранее неизвестно количество изменений переменной цикла и её конечное значение.В зависимости от местонахождения блока проверки условия итерационные циклы могут быть организованы как циклы с предусловием (блок проверки условия размещён после тела цикла). Если в цикле с предусловием входящие в тело цикла команды могут не выполняться ни разу (если начальное значение параметра цикла удовлетворяет условию выхода из цикла), то в цикле с постусловием – выполняются как минимум один раз (даже если начальное значение параметра цикла удовлетворяет условию выхода из него). Пример 2.2 Дан ряд натуральных чисел 1, 2, 3, …,  и число n. Требуется найти сумму первых членов ряда. Вычисление суммы прекратить, как только её значение будет равно или превысит заданное число n. Вариант схемы алгоритма решения задачи, включающей итерационный цикл с постусловием, приведён на рис. 2.2,а. Цикл организован в виде итерационного потому, что число его повторений заранее неизвестно. В алгоритме выход из цикла или его продолжение определяется выполнением (или невыполнением) условия s >= n в блоке 6. Если условие не выполняется, вычисление суммы продолжается путём прибавления к предыдущему значению суммы (переменной s) значения очередного члена ряда, отслеживаемого переменной цикла i. Однако приведенный алгоритм дает неверное решение при n = 0, так как в этом случае не будет выполнено первое по порядку сравнение s = n = 0. Правильный алгоритм решения этой задачи с использованием итерационного цикла с предусловием приведён на рис. 2.2,б. В этом алгоритме тело цикла расположено после проверки условия выхода из него. В нем в начале осуществляется проверка s ≥ n(блок 5), и если nзадано равным нулю, то тело цикла не будет выполняться ни разу.
Вид итерационного цикла (с пост- или предусловием) определяется условием задачи и допустимыми или возможными значениями исходных данных. Например, при решении задачи 2.3 возможно использование итерационного цикла только с нижним окончанием, так как, для того чтобы выполнить проверку на окончание счета, необходимо сравнить значения двух последних членов ряда. Пример 2.3 Дано натуральное n и первый член бесконечного ряда: y1 = 1. Вычислить сумму членов бесконечного ряда, образованного по следующему рекуррентному соотношению: yi = 2yi-1 (то есть s = 1 + 2 + 4 + 8 + 16 + ...). Вычисление суммы продолжать до тех пор, пока соблюдается условие: |yi-yi-1| < n. Блок-схема алгоритма решения этого примера представлена на рис. 2.3. В задаче число учитываемых при суммировании членов ряда заранее не задано, следовательно, применяем итерационный цикл. При решении задачи обходимся без образования одномерного массива y1, y2, y3, … , вычисляя в цикле значения суммы предыдущего aи последующего b членов ряда. Как только разница между предыдущим aи последующим bчленами ряда по абсолютному значению станет меньше n, вычисление суммы прекращаем. При организации цикла с постусловием необходимо помнить, что при любых начальных значениях исходных данных тело цикла обязательно будет выполнено хотя бы один раз. Если же организовать цикл с предусловием, то необходимо быть уверенным в том, что начальное значение исходных данных позволяет проверить условие выхода из цикла без его выполнения. С циклическими вычислительными процессами связаны также задачи с обработкой массивов. Массивом принято называть упорядоченную совокупность однотипных данных, имеющих общее имя. Элементы массива отображаются именем массива, за которым следует один, два или более индексов. Если индекс один, то массив является одномерным, при этом индекс указывает порядковый номер элемента в массиве: x1, x2, ..., xn . Если индексов два, то массив является двумерным, при этом первый индекс указывает номер строки элемента массива, а второй - номер его столбца.  12 3 4 5 7 6 да нет 8 9 Рис. 2.3. Вариант блок-схемы алгоритма решения примера 2.3 Пример 2.4 Найти количество элементов, больших среднего арифметического массива x1, x2, ..., xn. Как следует из поставленной задачи, сначала необходимо просуммировать элементы массива с x1 до xn, а затем для получения среднего полученную сумму s разделить на n, т.е. xср = s / n. Потом взять каждый из элементов массива xi и, изменяя i от 1 до n, проверять xi > xср, если условие будет выполняться, то переменную количества таких элементов k увеличивать на 1, если же нет, то значение k оставлять без изменения. Блок-схема алгоритма решения этой задачи приведена на рис. 2.4.
В данном алгоритме в блоке 2 осуществляется ввод числа элементов массива n. В цикле (блоки 3 и 4) осуществляется поочередный ввод всех элементов массива (x1, x2, x3..., xn ). В блоке 5 принимается первоначальное значение суммы элементов, равное 0. Циклический фрагмент алгоритма (блоки 6 и 7) осуществляет накопление элементов массива через операцию присваивания s = s + xi: при i = 1 s = s + xi , 0 + x1, при i = 2, s = s + xi = x1 + x2, при i = 3 s = s + xi = s + x1 + x2 + x3 и т.д. Значение s = 0, принятое в блоке 5, обнуляет регистр ПЭВМ, в котором будет накапливаться сумма при выполнении цикла. В блоке 8 вычисляется среднее значение элементов массива. В блоке 9 обнуляется регистр k, обеспечивающий подсчёт количества элементов массива x, больших xср. В цикле алгоритма (блоки 10, 11, 12) осуществляется подсчёт количества xi, больших xср, через операцию присваивания k = k + 1 в случае выполнения условия xi > xср . Так, если при i = 1 x1 > xср , то k = k + 1 = 0 + 1 = 1, если же нет, то k остаётся без изменений, и т.д. при i = 2, 3, 4 …n. Пример 2.5 В массиве x1, x2, x3, x4, x5 ..., xn найти максимальный элемент и его порядковый номер, если же их несколько, то вывести все их порядковые номера. Пусть элементы массива будут следующие:
При нахождении максимального элемента max за максимальный принимается первый элемент: max = x1, т.е. max = 2. Далее следующий сравнивается с max (х2 > max), т.е. (6 > 2), и поскольку условие выполняется, то за максимальный необходимо принять следующий, т.е. 6. Это будет осуществлено присваиванием max = х2. Далее необходимо опять сравнить следующий с максимальным (х3 > max), т.е. 1 > 6, и поскольку условие не выполняется, то в качестве максимального необходимо оставить прежний, т.е. max=6. Затем опять сравнить следующий элемент х4 > max, и поскольку условие выполняется, то в качестве максимального присваиваем max = x4 и т. д. В блок-схеме алгоритма (рис. 2.5) при изменении индекса элемента i от 2 до n (блоки 6…8) находится максимальный элемент массива x.
Рис. 2.5. Блок-схема алгоритма решения к примеру 2.5 Цикл по i = 1 до n (блоки 10-12) обеспечивает вывод номеров i всех максимальных элементов при выполнении условия Xi = max. Однако при наличии только одного максимального элемента его номер можно определить без последнего цикла по i, добавив еще дополнительной переменной m операцию присваивания m = i в блоке 8, предварительно приняв в блоке 5 значение m = 1. Тогда в блоке 9 необходимо дополнительно осуществить вывод m и закончить алгоритм. Индивидуальные задания к лабораторной работе № 2 1-й вариант Для массива а1, а2, а3, … аn получить среднее арифметическое его положительных элементов. Напечатать таблицу перевода температуры из градусов по шкале Цельсия (С) в градусы по шкале Фаренгейта (F) для значений от 15°С до 30°С с шагом 1°С. (Перевод осуществляется по формуле: F = 1,8  ×C + 32.Имеется две группы комбайнов: 8 комбайнов ККУ-2А и 6 комбайнов – КПК-3. Комбайнами I группы выкопано соответственно p1, p2, … p8 тонн картофеля; II – r1, r2, … r6 тонн. Сравнить средние производительности комбайнов, сделать вывод, какой тип комбайнов лучше. Напечатать p и r средние и комментарий. 2-й вариант Вычислить 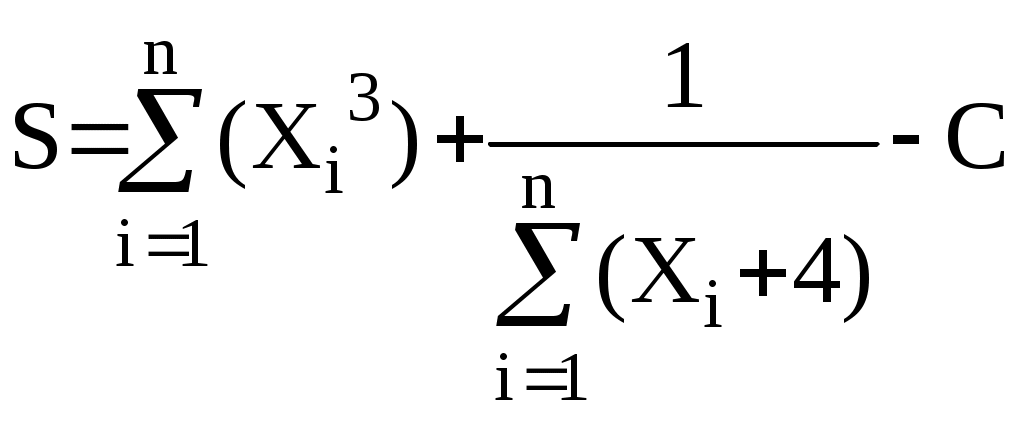 Вычислить приближённо площадь одной арки синусоиды, разделив отрезок от 0 до  на 10 частей и суммируя площади десяти прямоугольников с основанием / 10 и высотой, равной значению функции на правой границе каждого интервала.Дан список 5 студентов и отметки каждого из них за выполнение двух контрольных работ а1, а2,… а5 и b1, b2, … b5. Подсчитать число студентов, выполнивших обе работы на 9 или 10. 3-йвариант 1. Вычислить  2. Из массива a1, a2,… a10 получить массив b1, b2, … b10, в котором вначале следуют все отрицательные числа, затем все положительные. 3. Имеется 10 клубней I сорта весом p1 , p2,… p10 и 8 клубней II сорта весом r1, r2, … r8. Определить, клубни какого сорта в среднем тяжелее. 4-й вариант 1. Вычислить 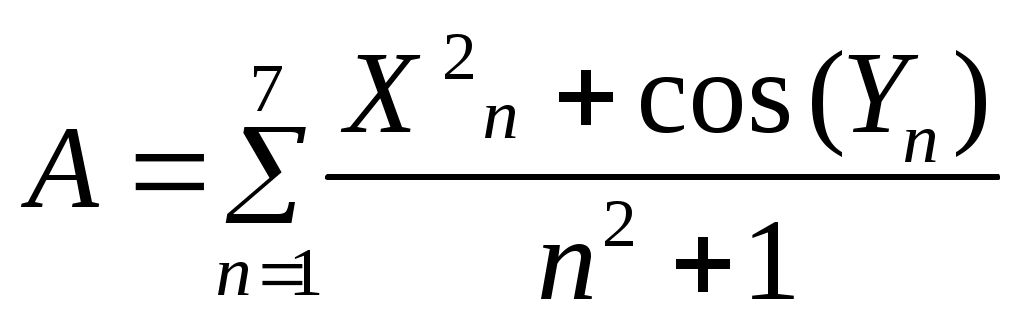 2. Из массива a1, a2, … a15 выбрать каждый 3-ий элемент и образовать массив B (где b1=a3, b2=a6, b3 =a9, …). 3. Подсчитать число чередований знака соседних членов с «+» на «-» или наоборот в последовательности чисел x1, x2, x3,… xn. 5-й вариант 1. Вычислить  2. Определить сумму 10 членов арифметической прогрессии, первый член которой равен a1, а разность между последующим и предыдущим равна p. 3. В течение n дней ежедневно производили замеры влажности почвы D1, D2,… Dn. Определить какого числа влажность почвы была наивысшей. 6-й вариант 1. Вычислить  2. Определить сумму t первых членов геометрической прогрессии, первый член которой равен a1, а знаменатель равен q. 3. Произвести расчёт диаметра провода d для различных значений тока i и допустимой плотности тока j. При расчёте использовать формулу:  . Значения тока i меняются в пределах от 0,1 до 1 c шагом 0,1.7-й вариант 1. Вычислить 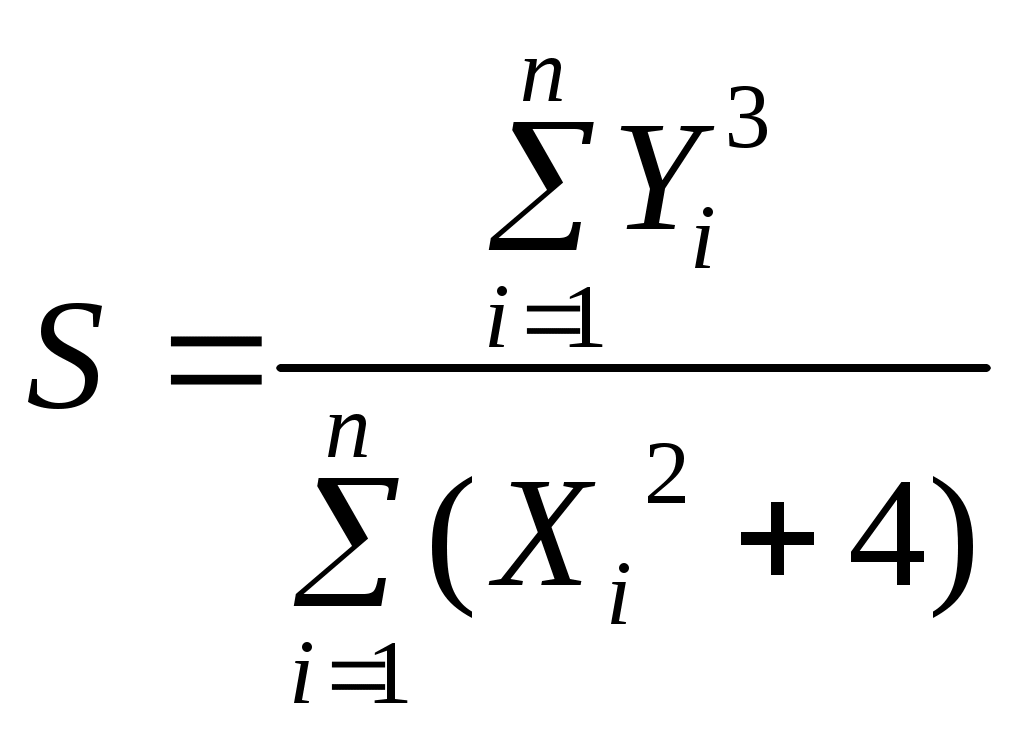 2. Если в массиве x1, x2, … xn есть хотя бы один член, равный a, то получить сумму всех членов, следующих за первым таким членом, в противном случае ответом должно служить сообщение об этом. 3. Проверить располагаются ли все номера телефонов в колхозном телефонном справочнике в порядке возрастания. 8-й вариант 1. Вычислить  2. Дан массив А1, А2, … Аn. Все неотрицательные элементы массива заменить на 1 и получить число неотрицательных элементов массива. Также вывести на печать полученный массив. 3. Оценки, полученные абитуриентом на вступительных экзаменах, составляют r1, r2, … rn баллов. Определить, поступит ли абитуриент в учебное заведение, если известно, что проходной балл составляет p. 9-й вариант Вычислить 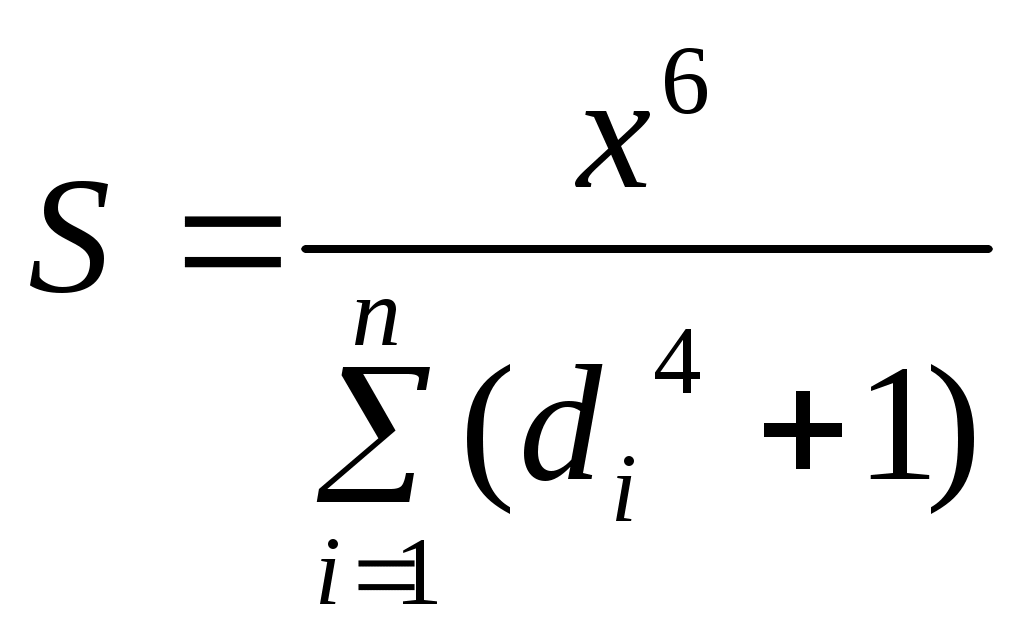 Получить произведение тех элементов массива с1, с2,… сn, которые превышают заданное число d. Даны номера выигрышных билетов p1, p2, … pn. Определить, является ли билет с номером r выигрышным. 10 –й вариант Вычислить S,  Даны целое число n и действительные числа a1, a2,…an. Получить “сглаженные” значения элементов, заменив все его элементы, кроме первого и последнего, по формуле  , считая, что для сглаживания используются лишь старые элементы массива.Массив r1, r2, …, r10 содержат сведения о том, на сколько меньше объём выпущенной продукции каждым из 10 отстающих рабочих бригады от плановых заданий. Определить, кто из рабочих имеет наибольшее отставание, и напечатать его порядковый номер. 11-й вариант 1. Вычислить R,  , для x, изменяющихся от 0,07 до 0,5 с шагом 0,03.2. Вычислить сумму квадратов первых n натуральных чисел. 3. За сезон уборки каждым из 10 комбайнов убрано соответственно p1, p2,…,p10 гектаров поля. Определить, сколько комбайнов достигли плановой наработки a. Искомое количество напечатать. 12-й вариант Вычислить  .Дан массив a1, a2, …, an. Все элементы массива, принадлежащие отрезку [c, d], распечатать и заменить нулями. Если указанных элементов нет, напечатать соответствующее сообщение. Найти вес заготовки из материала с удельным весом w, имеющей форму прямоугольного параллелепипеда с высотой h и сторонами основания a и b, учитывая, что в заготовке параллельно высоте просверлено n неперекрещивающихся между собой сквозных отверстий с диаметрами d1, d2, d3, …, dn. 13-й вариант 1. Вычислить Y при x > 64,  2. Даны действительные числа a1, a2, …, an. Все отрицательные элементы массива заменить их квадратами и подсчитать сумму положительных элементов данного массива. Полученный новый массив вывести на печать. 3. Проверить чередование знаков соседних членов массива из n действительных чисел. Если это чередование выполняется на протяжении всей последовательности чисел, то вывести на печать первые два члена массива, если же не выполняется, то вывести на печать первые два соседних члена с одинаковыми знаками. 14-й вариант 1. Вычислить  2. Если элементы массива a1, a2, a3, ... an образуют возрастающую последовательность, то получить сумму элементов массива, в противном случае получить их произведение. 3. За сезон уборки каждым из комбайнов убрано соответственно s1, s2, … s8 га поля. Определить, достигает ли средняя наработка комбайнов плановой p. 15-й вариант 1. Даны координаты n точек: (х1, у1); (х2, у2); (х3, у3)); …; (хn, yn). Определить, сколько точек попадает в кольцо с внутренним радиусом r1 и внешним r2, если центр кольца находится в начале координат. 2. Имеется список n членов бригады с указанием их года рождения. Определить средний возраст и вывести порядковые номера членов бригады, возраст которых превышает средний. 3. Имеются сведения о количестве тракторов, которые должны быть поставлены по плану каждому из 10 колхозов a1, a2, …, a10. Также имеются сведения о фактической поставке тракторов этим колхозам b1, b2, …, b10..Скольким колхозам недопоставлены трактора? Вопросы для самоконтроля 1. Какой вычислительный процесс называется циклическим? 2. Чем определяется конец циклического вычислительного процесса? 3. Что представляет собой массив данных? 4. Какие величины могут использоваться в качестве переменной или параметра цикла? 5. Как классифицируются циклы? 6. Какой цикл называется детерминированным? Лабораторная работа № 3 | |||||||||||||||||||||||||||||
1
6
нет
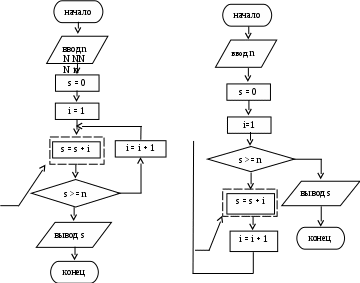1
ело цикла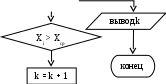
1
3
