Учреждение образования
 Скачать 0.61 Mb.
|
|
Тема: Решение задач, имеющих алгоритмы с вложенными циклами. Цель: Приобрести навыки математической формулировки содержательной постановки задачи, выбора метода, разработки алгоритма и программы её решения. Понятие вложенного цикла тесно связано с понятием внешнего и внутреннего цикла. Блок-схема алгоритма с одним вложенным циклом приведена на рис. 4.1.  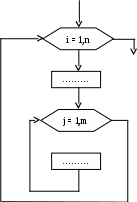 i > n Рис. 4.1. Блок-схема алгоритма вложенным циклом Как видно из рисунка, цикл по j вложен в цикл по i и по отношению к нему является внутренним, а цикл по i – внешним. Из схемы алгоритма следует, что при i = 1 цикл по j повторяется m раз, т.е. на 1 внешний цикл по i приходится m внутренних по j, поэтому общее число циклов в данном алгоритме будет n  m. В алгоритмах может быть любое число вложенных циклов. Циклы с одним вложением обычно используются при обработке таблиц, состоящих из строк и столбцов и имеющих вид двумерных массивов. В таких массивах положение элемента и его значение определяется номером строки и номером столбца:а11 а12 а13 … а1m a21 a22 a23 …a2m a31 a32 a33 … a3m ………………. an1 an2 an3 … anm Имя элемента такого массива будет аi,j. Первый индекс i указывает на номер строки, а второй j – на номер столбца. Тогда при работе с элементами каждой строки массива необходимо зафиксировать первый индекс i, а изменять второй индекс j, что сможет обеспечить блок-схема алгоритма на рис. 4.2. При работе с элементами каждого столбца необходимо зафиксировать второй индекс j, а изменять первый индекс i, что обеспечивает блок-схема алгоритма на рис. 4.3.  Рис. 4.2. Блок-схема алгоритма Рис. 4.3. Блок-схема работы с элементами строки алгоритма работы с элементами столбца Учитывая, изложенное выше, рассмотрим следующую задачу по обработке двумерного массива. Пример 4.1 В матрице а (n  m), состоящей из n строк и m столбцов, определить номер строки с максимальным средним значением её элементов, если таких строк несколько, то выдать все их номера.Как следует из поставленной задачи, необходимо суммировать элементы каждой строки и полученную сумму делить на количество элементов в строке, т.е. m. Для выполнения этого во внешнем цикле должен быть первый индекс i, а во внутреннем - второй индекс j. Тогда накопление суммы элементов каждой из строк будет осуществляться по выражению: s = s + ai,j, а среднее значение элементов каждой строки можно получить по выражению asi =s/m. Из полученного одномерного массива средних значений asi остаётся найти максимальный элемент и его номер, который будет соответствовать номеру строки. Блок-схема алгоритма решения данной задачи приведена на рис. 4.4. В данном алгоритме блоки (3…5) обеспечивают построчный ввод всех элементов матрицы. Блоки (6…10) обеспечивают получение средних значений элементов каждой из строк матрицы. Причём его внутренний цикл (блоки 8…9) осуществляет суммирование элементов каждой из строк, и при выходе из него в блоке 10 определяется среднее значение элементов каждой строки и формируется одномерный массив. В блоках 11…14 находится максимальное значение элемента из средних asi. В блоках (16…18) выводятся порядковые номера элементов одномерного массива, равные наибольшему среднему, а сответственно и номера строк.   111 2 12 3 4 13 нет 14 5 6 15 7 16 9 19 8 17 нет 9 да 18 10 Рис. 4.4. Блок-схема алгоритма решения к примеру 4.1 Пример 4.2 Группа из n студентов сдала m экзаменов. Определить количество экзаменов со средним баллом более шести. Экзаменационная ведомость студентов имеет вид матрицы: х11 х12 х13 …x1m х21 х22 х23 …x2m …  ……………..хn1 хn2 хn3 …xnm Общий вид элемента xi,j, где первый индекс i указывает номер строки (студента), а второй индекс j – номер столбца (экзамена). Блок-схема алгоритма решения задачи приведена на рис. 4.5.   1 6 14 2 7 14 3 8  4 15 9 5 1110 12 нет да 13 Рис. 4.5. Блок-схема алгоритма решения к примеру 4.2 В данном алгоритме ввод элементов матрицы проведен построчно. Затем вначале обнуляется счётчик экзаменов (блок 6). Далее при j = 1 внутренний цикл по i = 1, n осуществляет суммирование баллов по каждому из экзаменов (s = s + xi,j) в блоках 9…10, предварительно принимая сумму баллов для каждого экзамена равного нулю (s = 0). По выходе из внутреннего цикла вычисляется xср, и количество экзаменов увеличивается на единицу (k = k + 1) при xср > 6, а при невыполнении этого условия k остаётся прежним (блоки 11…13). После этого осуществляется выход во внешний цикл, и процесс повторяется для следующего экзамена (j = 2) и т.д. Индивидуальные задания к лабораторной работе № 4. 1- й вариант 1. Для матрицы b (n m) определить среднее арифметическое элементов каждого столбца матрицы.2. В матрице b (n n) найти среднее арифметическое всех тех строк, в которых есть отрицательный элемент главной диагонали.2- й вариант 1. В матрице a размерностью n m заменить на 1 все положительные элементы и на 0 - все отрицательные и вывести полученную новую матрицу.2. Подсчитать количество положительных элементов в каждом столбце матрицы a (n m).3- й вариант 1. Найти среднее арифметическое значение неотрицательных элементов матрицы a размерностью n m.2. В матрице a (n m) найти общее среднее арифметичекое всех столбцов, у которых первый элемент равен нулю.4- й вариант 1. В матрице b (n n) найти сумму всех элементов каждой строки, кроме элемента, стоящего на главной диагонали.2. Все элементы матрицы a (n n), расположенные выше главной диагонали, переписать по строкам, начиная с первой, в одномерный массив b.5- й вариант 1. Получить одномерный массив t1, t2, …, tm с количеством элементов, равным количеству столбцов двумерной матрицы, каждый элемент которого получает значение 0, если все элементы j-го столбца матрицы размерностью n m имеют значение 0 или значение 1 в противном случае.2. Из матрицы a (n n) получить новую b (n n), умножив элементы каждого столбца на элемент главной диагонали, находящейся в данном столбце. 6- й вариант 1. Из матрицы b (n n) получить новую c (n x n), умножив элементы каждой строки на элемент главной диагонали, находящийся в данной строке.2. Для матрицы a (n m) напечатать номера тех столбцов, сумма элементов которых положительна.7- й вариант 1. Для матрицы x (n n) вывести на печать суммы элементов каждого из её столбцов, у которых элемент главной диагонали отрицательный.2. Из матрицы a (n m) все положительные элементы по строкам от начала к концу, начиная с последней, переписать в одномерный массив b и вывести его на печать.8- й вариант 1. Для матрицы a (n m) найти средние арифметические тех строк, у которых первый элемент положительный.2. В каждом столбце матрицы a (n m) подсчитать количество элементов, равных нулю.9- й вариант 1. В матрице a (n m) подсчитать количество столбцов, сумма элементов которых положительна.2. Для каждой строки матрицы a (n n) подсчитать количество элементов, совпадающих с элементом, стоящим на главной диагонали соответствующей строки.10- й вариант 1. Для матрицы a (n m) напечатать номера тех строк, суммы элементов которых положительны.2. В матрице a (n m) вместо максимального элемента записать последний и вывести полученную матрицу на печать.11- й вариант 1. Для каждой строки матрицы a (n m) определить сумму элементов, меньших последнего элемента данной строки.2. В матрице a (n m) вместо минимального элемента записать последний и вывести полученную матрицу на печать.12- й вариант 1. В матрице a (n m) определить количество положительных и количество отрицательных элементов.2. Все отрицательные элементы матрицы b (n m) переписать по строкам от конца к началу, начиная с первой, в одномерный массив с и вывести его на печать.13- й вариант 1. Найти общую сумму элементов тех столбцов матрицы a (n m), сумма элементов каждого из которых положительна.2. Элементы каждой строки матрицы a (n x m) умножить на наибольший элемент соответствующей строки. 14- й вариант 1. Определить общую сумму наибольших элементов каждой из строк матрицы a (a m).2. Для матрицы a (n m) определить номер столбца, в котором наибольшее число положительных элементов.15- й вариант 1. В матрице a (n m) найти номера тех столбцов, у которых первый элемент больше второго.2. В матрице a (n n) найти среднее арифметическое значение элементов, превышающих среднее арифметическое элементов главной диагонали.Вопросы для самоконтроля 1. В чём особенность структуры вложенных циклов в сравнении с циклами без вложений? 2. Что такое матрица? Какой смысл имеют i и j в обозначении элементов матрицы аi,j? В чём отличие вложенного цикла при обработке элементов строк матрицы в сравнении с обработкой элементов её столбцов? Вложенные циклы могут быть только детерминированными? В каком сочетании могут использоваться внешний и внутренний циклы (только детерминированными, или только итерационными, или в любом сочетании)? Литература 1. Информатика: Базовый курс / Симонович С.В. [и др.]. - СПб.: Питер, 2001. 2. Экзамен по информатике. Основы алгоритмизации и программирования / Прищепов М.А., Степанцов В.П., Севернёва Е.В. - Минск: Тетра Системс, 2001.- 192 c.: ил. 3. Программирование на языках Basic, Pascal и Object Pascal в среде Delphi / Прищепов М.А., Севернёва Е.В., Шакирин А.И. -Минск: Тетра Системс, 2006.- 320 c.: ил. Учебное издание МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ПРИКЛАДНЫХ ЗАДАЧ И АЛГОРИТМИЗАЦИЯ ИХ РЕШЕНИЙ Методические указания к лабораторным занятиям по дисциплине «Вычислительная техника и информатика» Составители: Прищепов Михаил Александрович Исаеня Николай Васильевич Ответственный за выпуск Н.В. Исаеня Редактор Н.Ф.Крицкая Компьютерный набор, верстка Н.В. Дайнеко Подписано в печать 22.08.2006 г. Формат 60×841/16 Бумага офсетная. Гарнитура Times New Roman. Усл. печ. л. 3,26 Уч.-изд. л. 2,55. Тираж 250 экз. Заказ Издатель и полиграфическое исполнение Белорусский государственный аграрный технический университет ЛИ № 02330/0131734 от 10.02.2006. ЛП № 02330/0131656 от 02.02.2006. 220023, г. Минск, пр. Независимости, 99, к. 2 |