Учреждение образования
 Скачать 0.61 Mb.
|
|
Тема: Решение задач, имеющих алгоритмы на итерационные циклы. Цель: Приобрести навыки математической формулировки содержательной постановки задачи, выбора метода, разработки алгоритма и программы её решения. В лабораторной работе № 2 число повторений (циклов) было известно заранее либо определялось простыми расчётами из исходных данных, т.е. рассматривались циклы с известным числом повторений. Во многих циклических процессах число повторений, необходимых для решения задачи, заранее определить невозможно, так как один или несколько параметров, определяющих условие выхода из цикла, вычисляются в теле цикла. Такие циклические алгоритмы, в которых заранее неизвестно число повторений и выход из цикла происходит по выполнению определённого условия, как уже указывалось в предыдущей работе, называются итерационными. Пример 3.1. Вычислить значение суммы бесконечного ряда  для любых значений  с учётом последнего члена ряда, учтенного в сумме, по модулю меньшего  .Как видно из условия, любой член ряда будет вычисляться по рекуррентной формуле  , при n = 1, 3, 5, … С возрастанием номера слагаемого его величина будет уменьшаться. Поэтому количество вычислений в цикле будет зависеть от выполнения условия  .Возведение в степень x проводилось путем умножения значения предыдущей степени на (x×x). Это позволяет уменьшить погрешность вычисления степени. Блок-схема этого примера приведена на рис. 3.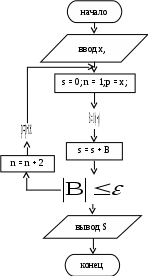1.  12 3 4 8 5 7 4 6 9 10 Рис. 3.1. Блок-схема алгоритма решения к примеру 3.1 Пример 3.2 Составить алгоритм вычисления суммы членов следующего ряда:  при значениях 0 < x < 1. Накопление суммы продолжать до тех пор, пока последний, учтённый в сумме член ряда не станет по модулю  .  Как видно из приведённой записи суммы, при указанных x с увеличением числа элементов ряда числитель будет уменьшаться, а знаменатель каждого слагаемого будет увеличиваться, поэтому их суммирование необходимо закончить, добавив к сумме последнее слагаемое, которое станет по модулю £  . Общий вид формулы для вычисления любого члена данного ряда:  , где n принимает значения  .При вычислении знаменателя каждого слагаемого в данном случае необходимо вычислять произведение  . Однако, как видно из примера, знаменатель третьего слагаемого отличается от второго множителем 3, четвёртого – от третьего множителем 4 и т. д., что делает возможным вычисление знаменателя последующего слагаемого через предыдущий. В данном случае с целью обеспечения быстродействия вычислительного процесса последующий член ряда An+1 можно получить путём умножения предыдущего An на некоторый постоянный для данного ряда множитель С, определяемый по формуле: Для данного ряда: 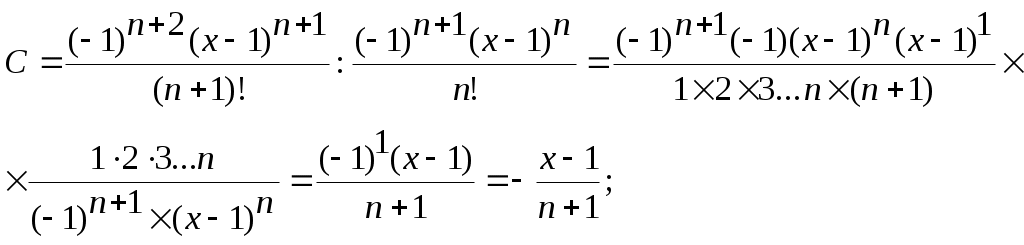 Тогда вычисление последующего члена ряда A через предыдущий можно вести по формуле:   Следовательно, приняв первоначально А = (х – 1) и далее умножая его на множитель 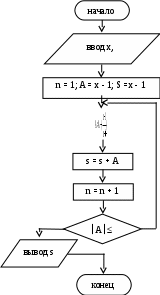 при n= 2, 3, 4, …, будем получать слагаемые суммы S, которые необходимо суммировать до тех пор, пока последнее не станет по модулю £. . Блок-схема такого алгоритма накопления суммы приведёна на рис. 3.2. 12 3 4 5 6 7 да нет 8 9 Рис. 3.2. Блок-схема алгоритма накопления суммы к примеру 3.2 В данном алгоритме первоначальное значение S принято равным х 1, т.к. при первом вычислении в цикле сразу будет получено второе слагаемое. Существует также определённый тип задач, в которых циклические вычислительные процессы продолжаются до выполнения или невыполнения определённого физического условия. Примером такой задачи может быть следующая. Пример 3.3 Мяч диаметром d, падая с высоты h и ударяясь о твёрдую поверхность, поднимается на 2/3 его предыдущей высоты. Определить, через сколько ударов он окажется на поверхности. Физическая модель данного процесса приведена на рис. 3.3. d 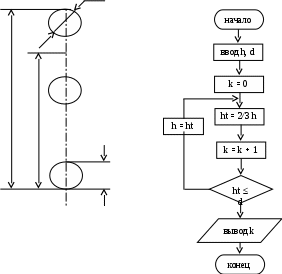 12 3 7 4 ht 5 h ht 6 Рис. 3.3. Физическая модель 8 к примеру 3.3 9 Рис. 3.4. Блок-схема алгоритма решения к примеру 3.3 Как видно из рисунка, новая высота ht после первого удара о поверхность будет 2/3 от предыдущей, т.е.  После второго удара следующая высота подъёма опять будет 2/3 от предыдущей высоты ht. Поэтому, чтобы опять воспользоваться формулой вычисления высоты ht = 2/3 h, необходимо присвоить h = ht и увеличить количество ударов k на 1. Данный циклический процесс, согласно рис. 3.4, будет повторяться, пока мяч не окажется на поверхности, т.е. последнее ht £ d. В данном алгоритме диаметр мяча d не участвует в вычислении высоты, а используется в условии проверки окончания вычислительного процесса.Индивидуальные задания к лабораторной работе № 3 1-й вариант 1. Вычислить сумму членов ряда:  . Суммирование прекратить, когда последнее слагаемое, учтённое в сумме, по модулю будет  .2. Дано действительное число a > 3. Среди чисел 1; 1+1/2; 1+1/2+1/3; 1+1/2+1/3+1/4, … найти первое большее a и подсчитать количество циклов для его определения. 3. Составить алгоритм деления натурального числа n на натуральное число m методом последовательного вычитания с печатью частного и остатка. 2-й вариант 1. При х > 1 вычислить сумму членов ряда:  .Суммирование прекратить, когда последнее учтенное в сумме слагаемое будет  .2. Сбербанк выдаёт в кредит r рублей при условии, что ежемесячный прирост долга составляет 10 % от текущего значения долга и сверх того он увеличивается на p рублей ежемесячно. Определить, через сколько месяцев долг превысит q рублей. 3. Дано 0 < a < 0,1. Найти наибольшее число вида 1/3n, которое будет меньше a при изменении n = 1, 2, 3, … 3-й вариант 1. При  <1 вычислить сумму членов следующего ряда:  . Суммирование прекратить, когда последнее слагаемое, учтённое в сумме, по модулю будет  .2. Начав тренировки, спортсмен в первый день пробежал a км. Каждый следующий день он увеличивал свою дневную норму на 13 % от нормы предыдущего дня. Определить, через сколько дней спортсмен будет пробегать в день больше 10 км. 3. При  вычислить сумму членов ряда:  Суммирование прекратить, когда последнее учтённое в сумме слагаемое станет .4-й вариант 1. Вычислить сумму членов ряда:  . Последним учтенным в сумме членом ряда должен быть член  .2. Одноклеточная амёба через каждые 3 часа делится на 2 клетки. Определить, через сколько часов будет m клеток. 3. Дано два положительных числа a и b, причём b намного больше a. Найти наименьшее значение n, при котором s = a + a2 + a3 + … an станет больше b. 5 -й вариант 1. Для  вычислить сумму членов ряда:  . Вычисления прекратить, когда первый неучтённый в сумме член ряда станет по модулю £ .2. В 2005 году урожай ячменя составил r ц с гектара. В среднем каждые 2 года за счёт применения передовых агротехнических приёмов планируется урожай увеличить на k % по отношению к предыдущему году. Определить, через сколько лет урожайность достигнет p ц с гектара. (p>r). При <1 вычислить  . Вычисления прекратить, когда первый учтённый в сумме член ряда станет по модулю £  .6-й вариант 1. Для чисел 0 < x < 1 вычислить значение суммы  . Вычисления прекратить, когда первый учтённый в сумме член ряда станет £ .2. Концентрация хлорной извести в бассейне составляет r г/л. Через трубу в бассейн вливают чистую воду со скоростью q м3/ч, а через другую трубу с той же скоростью вода выливается. Концентрация хлорной извести изменяется по закону:  ,где t – время, c – концентрация в предыдущий момент времени, n – параметр её изменения. Через сколько часов концентрация достигнет безопасной для человека величины p г/л (p < r)? Рассчитывать концентрацию через 1, 2, 3,… часа, используя в расчётах каждый раз концентрацию с предыдущего часа.3. Дано число 0 < a < 0,5. Найти наименьшую целую степень k, при которой число вида 7/3k станет меньше a. 7-й вариант 1. Вычислить значение суммы ряда:  . Учтёнными в сумме ряда должны быть только члены  .2. Плотность воздуха P с высотой убывает по закону:  , где Pn – начальная плотность воздуха, h – высота, z – параметр убывания плотности. Определить, на какой высоте плотность воздуха будет меньше r. Рассчитывать плотность воздуха по высоте через 1 м. 3. Дано число 0 < a < 0,1. Найти наименьшею целую степень n, при которой число вида 1/3n станет меньше a. 8-й вариант 1. Вычислить значение суммы ряда:  . Учтёнными в сумме ряда должны быть только члены  .2. В течение месяца бригада за каждый день работы выпускает на r изделий больше предыдущего. В первый день было выпущено d изделий. Определить, через сколько дней бригада выполнит месячную норму a. Если в течение месяца (26 рабочих дней) норма не будет выполнена, то напечатать соответствующее сообщение. 3. Дано число 0 < b < 0,000002. Найти наименьшую целую степень при которой число вида  станет < b. 9-й вариант 1. При b > 0 вычислить значение суммы ряда:  . В сумму должны войти вcе члены ряда > .2. В пустую ёмкость объёмом q м3 один насос производительностью p1 м3/ч подаёт жидкость, а другой производительностью p2 м3/ч одновременно откачивает (причём p2 < p1). Кроме того, каждый час дополнительно 10 % содержимого ёмкости расходуется. Определить, через сколько часов необходимо отключить подающий насос, чтобы не произошло переполнение ёмкости. 3. Для любого 0 < x< 5 найти сумму ряда:  . В сумму должны войти все члены > .10-й вариант 1. Для любого а > 1 определить произведение членов ряда  . В произведение должны войти все члены  .В резервуаре находится q м3 летучего вещества. По истечении каждого часа Р % от текущего содержимого резервуара улетучивается и r м3 порционно расходуется. Определить, через сколько времени резервуар опустеет (r < q). Определить, в какую целую наибольшую положительную степень необходимо возвести число b > 1, чтобы результат не превосходил заданной величины a . 11-й вариант 1. Для  вычислить значение суммы ряда:  . Вычисления прекратить, когда первый учтённый в сумме член ряда станет по модулю £ .2. В ёмкости находится q м3 жидкости. После работы в течение 1 часа откачивающего насоса производительностью p1 м3/ч дополнительно подключится подающий насос производительностью p2 м3/ч (причём p1 > p2). Определить, через какое время от начала работы первого насоса ёмкость опустеет, если, кроме того, в конце каждого часа порционно расходовалось p % от содержимого ёмкости. 3. Число a возводят в квадрат и результат увеличивают на 2. Полученное число снова возводят в квадрат и результат увеличивают на 2. Этот процесс продолжают до тех пор, пока не будет получено число x, большее 100 000. Определить, через сколько циклов будет получено число x. 12- й вариант 1. Для 0 < x < 1 вычислить значение суммы ряда:  . В сумму должны войти все члены ряда >  .2. На сберкнижку положен вклад w руб. Определить, через сколько месяцев сумма вклада превысит s руб., если известно, что ежемесячно она увеличивалась на p % от текущей суммы и со счёта снималось r руб. При этом ежемесячный прирост по процентам больше ежемесячного расхода, т.е.  .3. Определить, в какую наибольшую целую положительную степень необходимо возвести число 1/b, где 1 < b < 2, чтобы результат не превосходил 0,0001. 13- й вариант 1. Вычислить значение суммы ряда:  . В сумму должны войти все члены ряда > .2. Образовать массив, в котором каждый последующий элемент больше предыдущего на с. Первый элемент принять равным 1, а вычисления прекратить, когда последний элемент массива станет > d. Число a > 1,1 возводят в четвёртую степень и результат уменьшают в 1,2 раза. Этот процесс продолжают до тех пор, пока не будет получено число x > 100 000 000. Определить, через сколько циклов будет получено число х. 14- й вариант 1. Найти среднее арифметическое ряда чисел, в котором каждый последующий член на 2 больше предыдущего. Причём первый элемент равен 1, а последний больше или равен заданному числу d. 2. Резервуар содержит t кг летучего вещества, которое расходуется равными порциями по p кг в конце каждых суток (P < t). Ежесуточно 0,5 % от текущего содержимого резервуара улетучивается. Определить, через сколько суток в резервуаре останется вещества меньше b кг. 3. Дано число 0,1 < c < 0,01. Найти наименьшую целую степень, при которой число вида 1/3n станет < c. 15- й вариант 1. Для 0 < x < 1 вычислить значение суммы ряда:  . В сумму должны войти все члены ряда .2. При 0 < |x| ≤ 1 вычислить значение суммы ряда:  . Вычисления прекратить, когда первый учтённый в сумме член ряда по модулю £ .3. Вычислить сумму ряда:  . В сумму должны войти все члены ряда по модулю > .Вопросы для самоконтроля 1. Какой цикл называется итерационным? 2. Какой итерационный цикл называется циклом с верхним окончанием, а какой с нижним? 3. Можно ли при программировании итерационного цикла использовать блок модификации? 4. Как будет проходить вычислительный процесс, если в алгоритме итерационного цикла не изменять параметр цикла? Лабораторная работа № 4 |