Учреждение образования
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
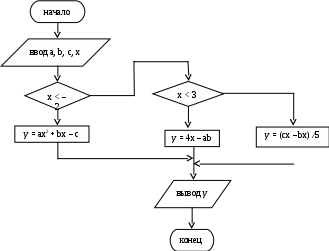
Министерство сельского хозяйства и продовольствия Республики Беларусь Учреждение образования«Белорусский государственный аграрный технический университет» Кафедра вычислительной техники МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ПРИКЛАДНЫХ ЗАДАЧ И АЛГОРИТМИЗАЦИЯ ИХ РЕШЕНИЙ Методические указания к лабораторным занятиям по дисциплине «Вычислительная техника и информатика» Минск 2006 УДК 004(07) ББК 32.97я7 М 54 Рекомендовано научно-методическим советом агроэнергетического факультета БГАТУ Протокол № 4 от 14 декабря 2005 г. Составители: д-р техн. наук, проф. М.А. Прищепов, канд. техн. наук, доц. Н.В. Исаеня Рецензенты: д-р техн. наук, проф. В.С. Муха, канд. техн. наук, доц. Ю.Н. Силкович УДК 004(07) ББК 32.97я7 © М.А. Прищепов, Н.В. Исаеня, 2006 © БГАТУ, 2006 Лабораторная работа № 1 Тема: Решение задач на разветвлённые алгоритмы. Цель: Приобрести навыки математической формулировки содержательной постановки задачи, выбора метода, разработки алгоритма и программы её решения. Процесс решения задачи на персональной ЭВМ (ПЭВМ) состоит из следующих основных этапов: 1. Постановка задачи. Математическая формулировка задачи. Выбор и разработка метода её решения. Разработка алгоритма решения. Программирование задачи. Отладка программы на ПЭВМ. Решение задачи по составленной программе на ПЭВМ. Анализ результатов решения. При непосредственном решении задач на ПЭВМ можно выделить три процедуры: ввод информации, обработка информации, вывод результата. Наиболее наглядным способом составления алгоритма является графический, т.е. изображение алгоритма решения в виде блок-схемы. При составлении разветвляющихся алгоритмов необходимо указать дальнейшее направление вычислительного процесса по одному из нескольких заранее определённых направлений в зависимости от выполнения некоторого логического условия. Пример 1.1 Составить алгоритм вычисления y для любых введённых значений x.  ax2 + bx-c, если x < –2 ax2 + bx-c, если x < –2y = 4x - ab, если –2 £ x < 3 (cx - bx) /5, если х ³ 3 В зависимости от положения x на числовой оси значение y необходимо вычислить по следующим формулам: y = ax2 + bx – c y = 4x – ab y = (cx – bx) /5       x x–2 3 x < – 2 –2 £ x < 3 x ³ 3 Данные вычисления могут быть реализованы по следующей блок-схеме алгоритма (рис.1.1). Пояснения к алгоритму. Ввод исходных данных а, b, c, x осуществляется в блоке 2. Затем в блоке 3 анализируется значение x, и если x < –2, то в блоке 4 вычисляется y по формуле: y = ax2 + bx – c, - и результат выводится в блоке 8. Если же x ³ –2, то из блока 3 идём по направлению «нет», и тогда значение x анализирует блок 5. Если x < 3, то из блока 5 идём по направлению «да», и значение y вычисляется по формуле: y = 4x – ab, - и также выводится в блоке 8. Если же x ³ 3, то из блока 5 идём по направлению «нет», и значение y вычисляется по формуле: y = (cx – bx) /5 - в блоке 7 и в блоке 8 выводится. Замечание. Следует обратить внимание на то, что для любого конкретного набора исходных данных вычисления, предписанные алгоритмом, пойдут только по одной ветви, хотя алгоритмом должны быть предусмотрены и определены все возможные ветви данного вычислительного процесса, т.е. обеспечиваться свойство массовости алгоритма.
Пример 1.2. Составить алгоритм определения наибольшего из трёх неравных между собой чисел a, b, c. Подумаем, какие действия необходимо выполнить для решения поставленной задачи (словесный способ записи алгоритма). Очевидно, что для определения наибольшего из трёх чисел можно предложить не один вариант. Первый вариант. Вначале следует сравнить первые два из трёх, затем большее сравним с третьим оставшимся числом, и большее число в этом последнем сравнении и будет наибольшим из трёх. Перед выводом этого числа на печать надо сначала его значение присвоить переменной р – это позволит сократить запись операторов вывода программы. Записав приведённые ниже рассуждения с помощью известных нам блоков, получим графический алгоритм её решения.
Второй вариант. Вначале сравниваем между собой первые два числа a и b (блок 3). Далее промежуточной переменной p присваиваем значение большего из них (блоки 4 или 5), а затем сравниваем её с третьим числом (блок 6). Если третье число с окажется больше этой промежуточной переменной p, то присвоим его ей (блок 7) и далее выведем её на печать (блок 8). Блок-схема этого алгоритма представлена на рис. 1.3.
Пример 1.3. Определить, можно ли поместить круг радиусом r в прямоугольник со сторонами a и b. Чтобы выяснить, какой должен быть ответ при любых a, b и r, обратимся к рис. 1.4. Как видно из рисунка, круг войдёт в прямоугольник, если диаметр круга будет меньше, чем меньшая из сторон прямоугольника. Тогда, возможные варианты блок-схем алгоритма решения представлены на рис. 1.5. 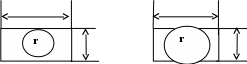 b b b b
Как видно из рисунка, круг войдёт в прямоугольник, если диаметр круга будет меньше, чем меньшая из сторон прямоугольника. Тогда, возможны варианты блок-схем алгоритма решения представлены на рис. 1.5.
На рис. 1.5, а определяется меньшая сторона прямоугольника (блок 3), а затем проверяется, чтобы диаметр круга был меньше, чем меньшая из сторон прямоугольника (блоки 4 и 6). На рис. 1.5, б проверяется вхождение круга в прямоугольник путём поочерёдного сравнения его диаметра с каждой из сторон (блоки 3 и 4). И, если он меньше их обоих, то круг можно поместить в прямоугольник. Пример 1.4 Среди трёх чисел x, y, z определить количество положительных чисел и их сумму. Блок-схема алгоритма решения представлена на рис. 1.6.
Индивидуальные задания к лабораторной работе № 1 1-й вариант 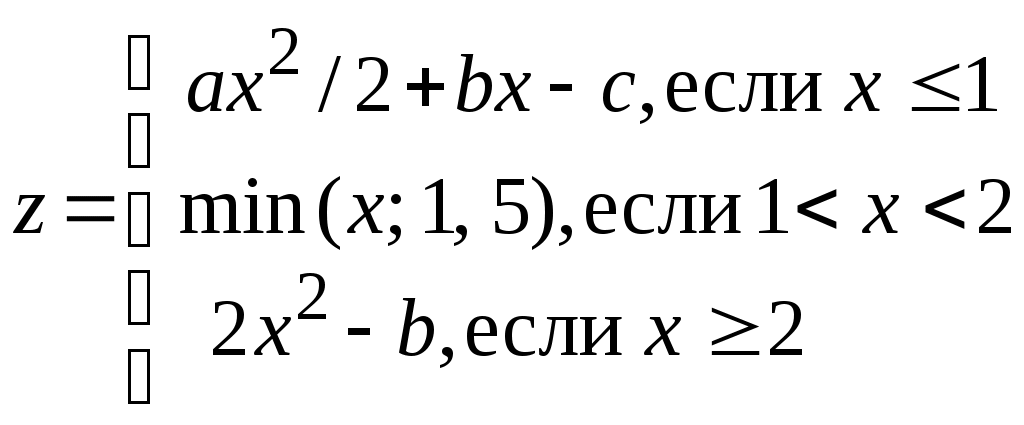 Проверить, является ли треугольник со сторонами a, b, c равнобедренным. Определить, попадёт ли команда «Динамо» в лигу сильнейших (т.е. наберёт не менее 20 очков). За выигрыш команда получает 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Всего команда провела n встреч. Из них m встреч выйграла, k – пройграла, а p завершила вничью. 2-й вариант 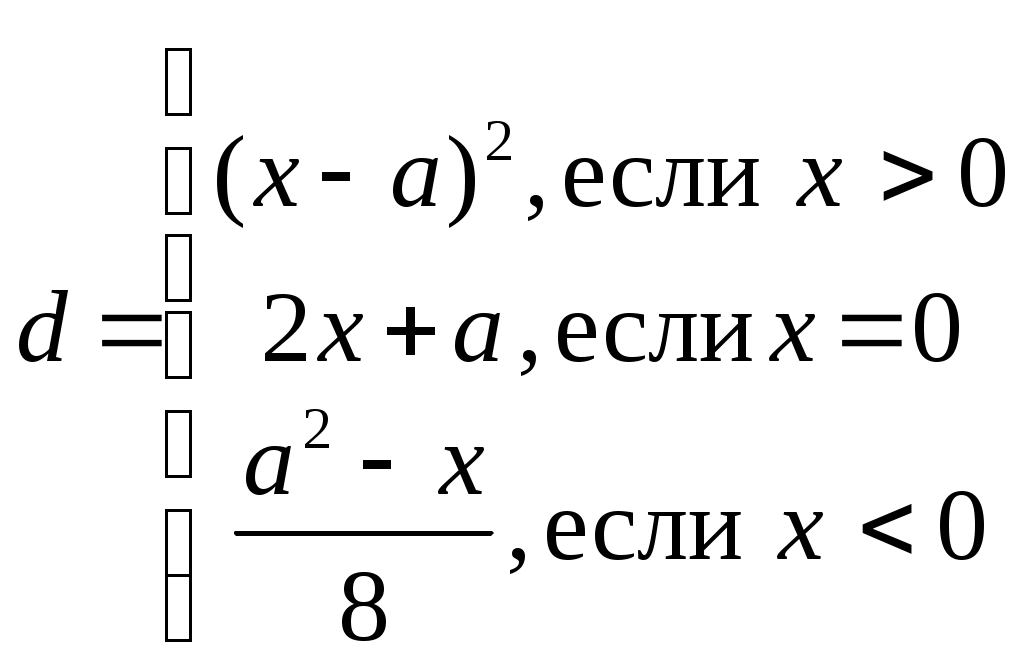 Определить, является ли число b наименьшим из трёх не равных между собой a, b, c. Для доставки на перерабатывающий завод продукции совхоз её сначала перевозит автотранспортом на железнодорожную станцию, а затем по железной дороге отправляет на завод. Недалеко от совхоза имеются две железнодорожные станции: станция А находится на расстоянии a1 км от совхоза и a2 км от завода; станция В – на расстоянии b1 км от совхоза и b2 км от завода. Определить, услугами какой станции совхозу выгоднее пользоваться, если стоимость перевозки 1 т продукции на расстояние 1 км составляет для автотранспорта c1 руб, для железнодорожного транспорта – c2 руб. 3-й вариант 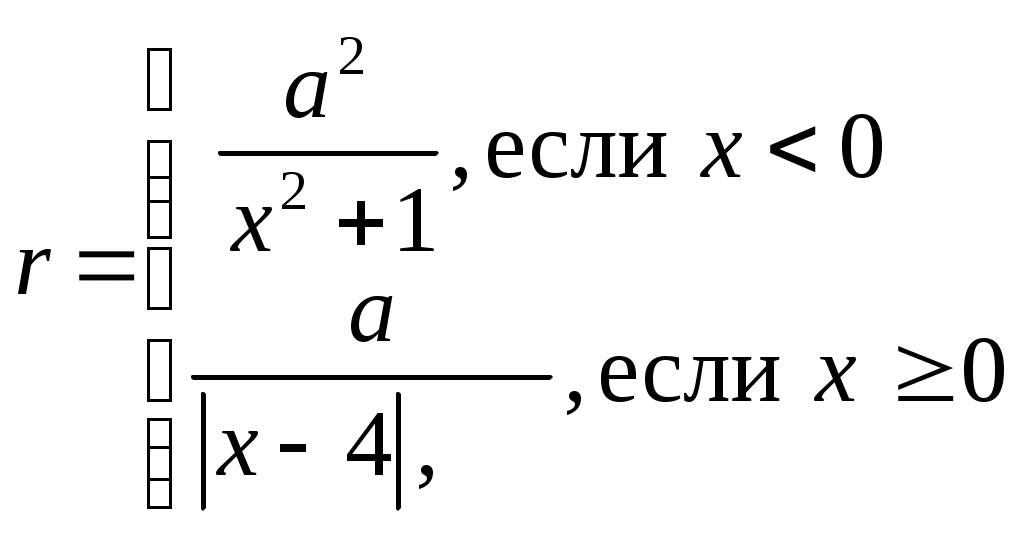 Определить, является ли треугольник со сторонами a, b, c прямоугольным (для определения использовать теорему Пифагора). Взвешивание поросёнка показало, что его масса за n дней увеличилась с m1 до m2 кг. Определить, достигнет ли среднесуточный прирост поросёнка запланированной нормы d. 4-й вариант  Определить, могут ли произвольные числа a, b, c служить длинами сторон треугольника. Имеются 3 клубня шарообразной формы радиусами r1, r2, r3. Определить, сколько из них пройдёт через отверстия сепарирующего решета площадью s, если они имеют форму круга. 5-й вариант 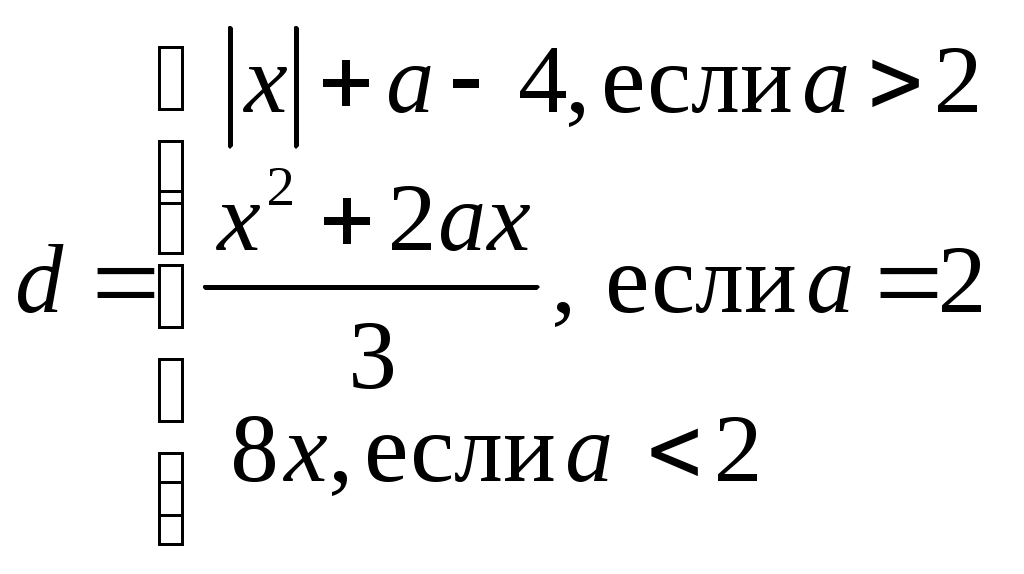 Составить алгоритм вычисления действительных корней квадратного уравнения ax2 + bx + c = 0 по формулам: x1,2 = Даны три неравных между собой числа a, b, c. Наибольшее из них разделить на сумму двух других. 6-й вариант Определить, какая из сторон a, b, c прямоугольного треугольника является его гипотенузой. Поле площадью S га убирали 3 комбайна с ежедневной выработкой R га в день, второе, площадью Q га, убирали 5 комбайнов с выработкой С га в день, а третье, площадью Р га, убирали 4 комбайна с ежедневной выработкой D га в день. Какое поле было убрано раньше всех? 7-й вариант 1. 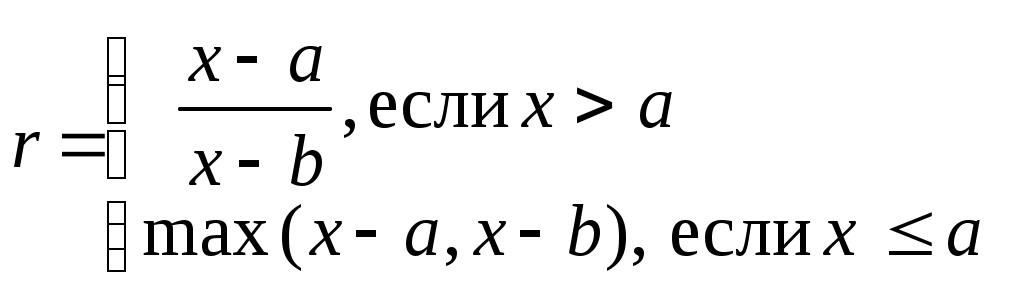 Определить, является ли треугольник со сторонами a, b, c равнобедренным. В бочке радиусом r и высотой h находится трёхкомпонентная механическая смесь: 40 % вещества А плотностью g; 32 % объёма вещества В плотностью k, остальной объём вещества плотностью c. Определить, можно ли увезти бочку транспортом грузоподъёмностью p. 8-й вариант  Вычислить Q = min (x, y2, z3) + 1. Определить, можно ли огородить изгородью длиной r земельный участок, имеющий форму равнобедренной трапеции с основаниями c и d и высотой h. 9-й вариант 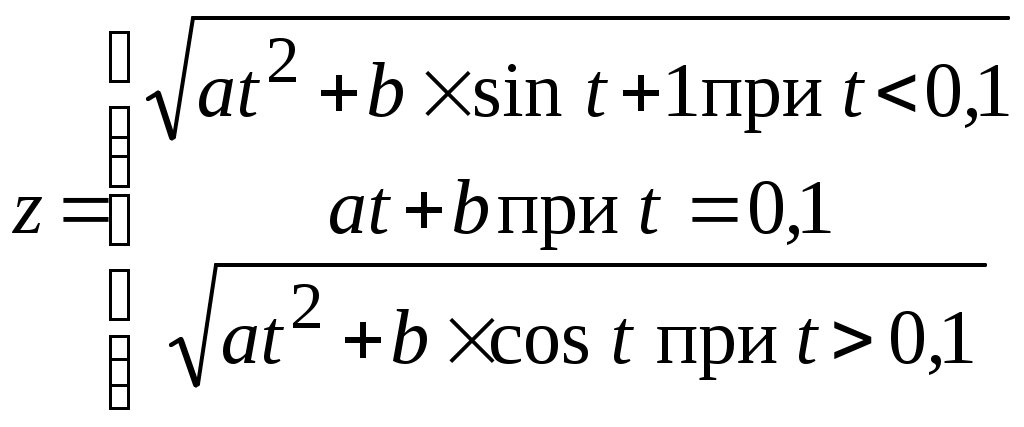 Даны три числа a, b, c. Напечатать те из них, которые больше 10. Определить, какая из трёх точек - А(x1, y1); В(x2, y2); С(x3, y3) лежит ближе к началу координат. 10-й вариант 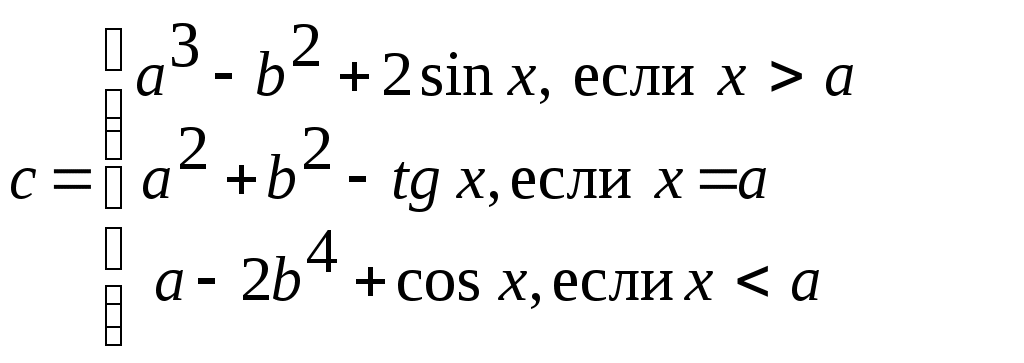 Определить количество неотрицательных чисел среди трёх a, b, c . Деревня А находится на расстоянии c км от железнодорожной станции и на расстоянии r км от другой деревни В ( см. рисунок 1.7). Определить, какая из деревень находится ближе к станции. ж/д станция   с 90° А r В Рис.1.7 11-й вариант  Проверить, является ли пара чисел (x1, y1) решением системы уравнений:  Имеется 10 луковиц размером r1, 6 луковиц размером r2 и 15 луковиц размером r3. Диаметр отверстия в сепарирующем решете p. Определить, сколько луковиц пройдёт сквозь отверстие решета. 12-й вариант 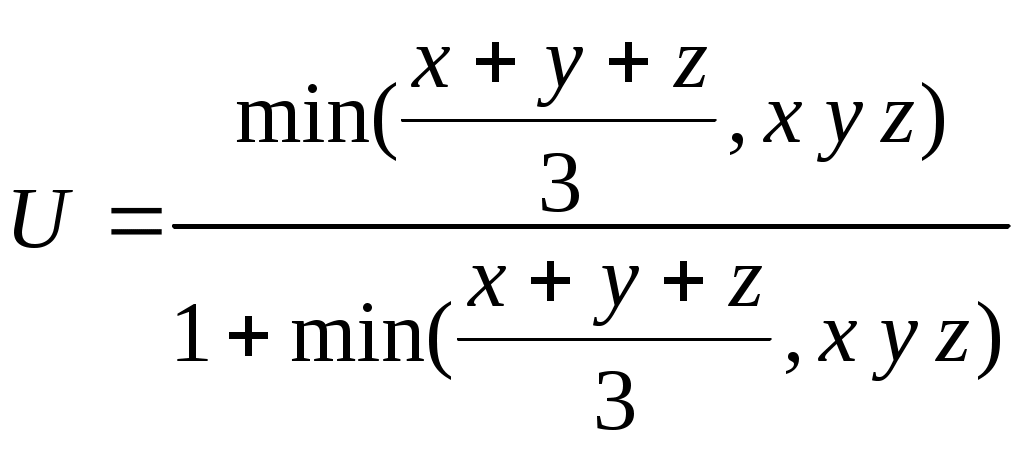 Определить, какие из 3-х точек с координатами (x1; y1), (x2; y2),(x3; y3) лежат в 3-й четверти. В колхозе имеется 5 комбайнов ККУ-2А со средней производительностью p га в день и 7 комбайнов КПК-3 со средней производительностью r га в день. Будет ли выполнена колхозом уборка поля площадью s га в запланированный срок, составляющий n дней? 13-й вариант 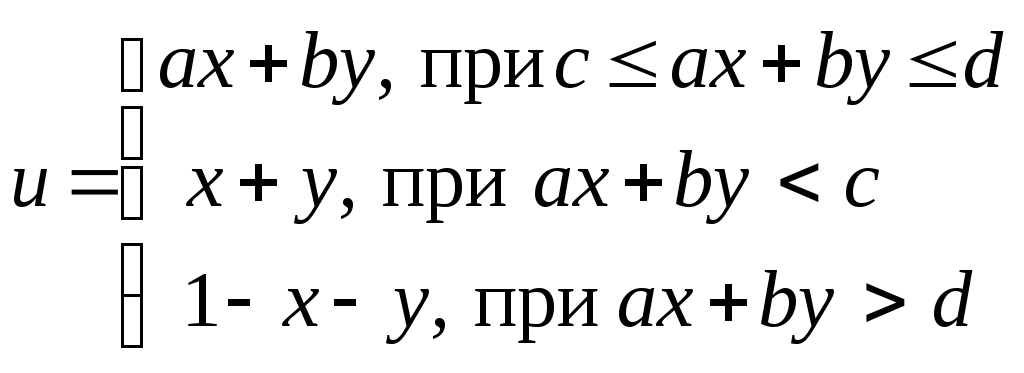 Задан квадрат с координатами по осям x и y: (2;2), (5;2), (5;5),(2;5). Если точка M(x1,y1) попадает внутрь этого квадрата, распечатать координаты этой точки. 3. В прядильном цехе имеется три машины разной производительности: на первой за 1 сутки можно изготовить n кг пряжи, на второй – m кг, а на третьей – d кг. В цех поступило p кг сырья. Обработает ли цех поступившее сырьё в запланированный срок, составляющий r дней? 14-й вариант 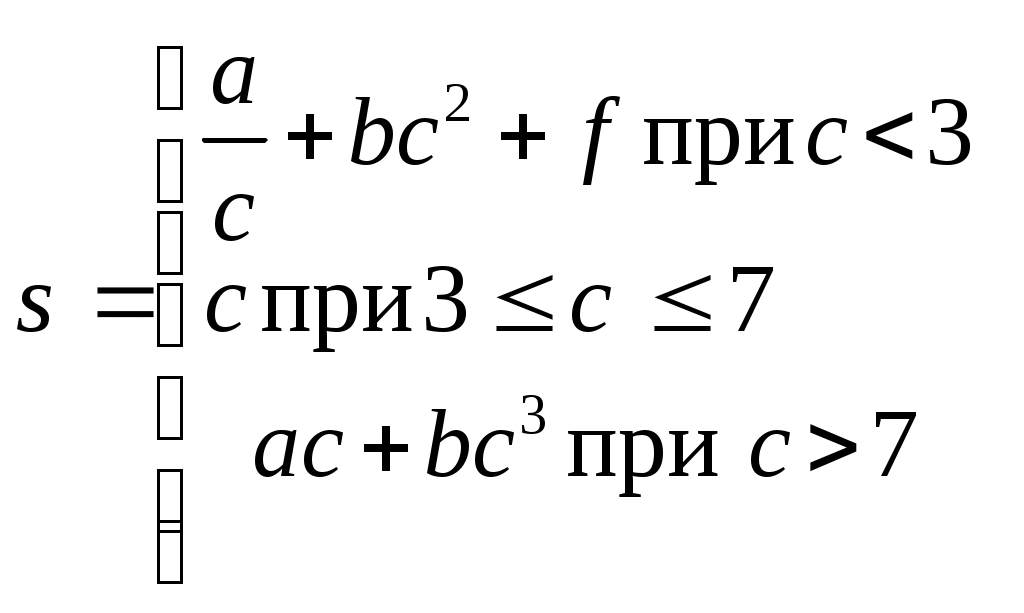 Даны две фигуры: квадрат со стороной a и круг радиусом r. Определить, какая из фигур имеет большую площадь, и вывести эту площадь на печать. Цех по переработке молочной продукции за одну смену выпускает пастеризованнго молока – a кг, кефира – b кг. Определить, выполнит ли цех план за месяц (30 дней) по каждому из видов продукции, составляющий соответственно s кг и p кг, если в первую декаду он работал в одну смену, во вторую – в полторы, в третью – в две смены. 15-й вариант  Среди трёх чисел a, b, c есть пара равных. Заменить их нулями. Суточная норма кормления одной коровы составляет a кг, одной лошади – b кг сена. Определить, можно ли прокормить k коров и m лошадей в течение n дней, располагая массой p кг сена, если нет, то рассчитать, сколько сена не хватает. Вопросы для самоконтроля Какие алгоритмы решения называют разветвляющимися? Что обеспечивает проверка логического условия в разветвляющемся алгоритме? Как выполняется алгоритм для конкретного примера с определённым значением исходных данных? Какими и с помощью скольких блоков можно разветвить процесс вычисления на 4 ветви? Может ли блок сравнения иметь по два выхода «да» или «нет» и почему? Могут ли логические связи, выходящие из выходов блока сравнения «да» и «нет», между собой быть непосредственно соединены? Лабораторная работа № 2 | ||||||||||||

 1
1 да да
да да 1
1 3 да 4 да 5
3 да 4 да 5 нет да
нет да
 1
1
 да 6 нет
да 6 нет 





 1
1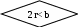 4 нет
4 нет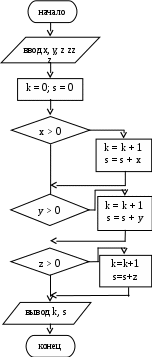 1
1