Инвестиции - Колтынюк Б.А.. Удк 336 ббк 65. 26 К 61
 Скачать 24.66 Mb. Скачать 24.66 Mb.
|
12.2. Доходность инвестиционного портфеляПри наличии определенной суммы денег и желания приобрести на них ценные бумаги на определенный промежуток времени инвестор каждый раз сталкивается с проблемой выбора инвестиционного портфеля. Сложность проблемы заключается в том, что, принимая решение в момент времени t = 0, инвестор не располагает необходимой и достаточной информацией о доходности сформированного таким образом портфеля. Все его предположения об ожидаемой или средней доходности различных ценных бумаг строятся на том, что в прошлом периоде времени доходность этих бумаг была достаточно приемлемой для их владельцев. С другой стороны, большинство инвесторов руководствуются соображениями, что недооцененные бумаги рынком будут «исправлены». Но это верно лишь в том случае, если и все другие инвесторы пользуются таким же подходом. При этом не следует забывать, что рынок «исправляет» лишь стоимость недооценных и переоценных активов. Причем если анализируется один вид ценной бумаги, то соответственно все предположения инвестора касаются только этой бумаги. В 1952 г. американский экономист (в будущем, в 1990 г., лауреат Нобелевской премии в области экономики) Гарри Марковиц опубликовал фундаментальную работу, которая является до настоящего момента основой подхода к инвестициям с точки зрения современной теории формирования портфеля. Согласно теории Г. Марковица, для принятия решения о вложении средств инвестору не нужно проводить оценку всех портфелей, а достаточно рассмотреть лишь так называемое эффективное множество портфелей и выбрать оптимальный. Инвесторы, стремясь максимизировать ожидаемую доходность, одновременно желают минимизировать риск. Наличие этих противоречивых друг другу целей затрудняем принятие решения о приобретении ценных бумаг на начальном этапе, т.е. в момент времени t= 0. Уменьшить влияние противоречивых друг другу целей рекомендуется с помощью покупки не одной, а нескольких бумаг, каждая из которых может отличаться не только доходностью, но и риском. Согласно уравнению (4.4) гл. 4 доходность ценной бумаги может быть вычислена по формуле: 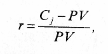 где С — будущая стоимость ценной бумаги; PV — текущая стоимость ценной бумаги или цена покупки. Если же учесть, что портфель состоит из N числа разных по стоимости ценных бумаг, то уравнение доходности можно записать в виде 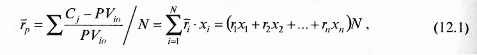 где р — среднеожидаемая доходность портфеля; хi — количество ценных бумаг i вида; ri — ожидаемая доходность ценной бумаги iвида; N— количество ценных бумаг в портфеле (i = 1, 2, 3,... N). Представленное выше уравнение доходности (12.1) отражает детерминированный подход к оценке доходности, когда о приобретаемых ценных бумагах известно все на момент времени t= 0 и через определенный промежуток времени владения ценными бумагами, т.е. на момент времени t = 1 инвестор получил вполне определенный доход. Однако, как уже отмечалось ранее, доходность ценной бумаги зависит от влияния множества факторов, которые в ряде случаев носят непредсказуемый характер поведения. Особенно большому влиянию множества факторов подвержены корпоративные ценные бумаги, меньшему — государственные. Поскольку деятельность всех участников фондового рынка осуществляется в условиях неполной определенности, то соответственно и исход практически любых операций купли-продажи ценных бумаг не может быть точно предсказан, т.е. остается случайным. Если это так, то инвестор вправе лишь только делать предположения относительно того, какие ценные бумаги должны входить в портфель в момент времени t= 0, считая при этом уровень доходности случайной переменной. Как известно, все переменные имеют свои характеристики, одна из них — ожидаемое (или среднее) значение доходности, а другая — стандартное отклонение случайной переменной, которая является мерой разброса ее возможных значений доходности. Иногда вместо стандартного отклонения используют дисперсию случайной переменной. Согласно теории Г. Марковица, при обосновании портфеля инвестор должен руководствоваться ожидаемой доходностью и стандартным отклонением. Интуиция при этом играет определяющую роль. Ожидаемая доходность рассматривается как мера потенциального вознаграждения, связанная с конкретным портфелем, а стандартное отклонение — как мера риска, связанная с данным портфелем. При этом делается важное предположение, что инвестор при всех прочих условиях предпочтет высокую доходность, если будут заданы два портфеля с одинаковыми стандартными отклонениями. Если же инвестору предстоит выбор между портфелями, имеющими одинаковый уровень ожидаемой доходности, то предпочтение отдается портфелю с минимальным риском, т.е., по сути, получению большего дохода при минимуме возможного отклонения. Для получения практических навыков в решении подобных задач рассмотрим следующий пример. Пример. Предположим, что мы сформировали инвестиционный портфель из трех ценных бумаг, каждая из которых за прошедший год составила: 42,8% (50-35)/35; 29,7% (42-37)/37; 35,3% (46-34)/34. Определим доходность портфеля и стандартное отклонение, считая, что число акций каждого типа равно соответственно 100, 100, 200. Тогда, подставив в формулу 12.1, получим ожидаемую доходность портфеля 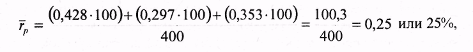 где 400 — общее число акций в портфеле. Поскольку ожидаемая доходность представляет собой средневзвешенные ожидаемые доходности, то вклад каждой ценной бумаги в ожидаемую доходность портфеля зависит от ее ожидаемой доходности, а также ее доли в начальной и конечной рыночной стоимости портфеля. Следовательно, в нашем примере наибольшую ожидаемую доходность получил бы инвестор, вложивший все имеющиеся у него средства в одну акцию с наибольшей ожидаемой доходностью. Однако большая часть инвесторов и их консультантов придерживается «золотых» правил инвестирования, одно из которых гласит: «нельзя вкладывать все средства в ценные бумаги. Необходимо всегда иметь резерв свободной денежной наличности для решения тех задач, которые могут возникнуть неожиданно». Другое общеизвестное правило — «нельзя складывать все яйца в одну корзину». Поэтому в практике портфельного инвестирования чаще всего используется диверсифицированный портфель, т.е. портфель с разнообразными ценными бумагами. Ожидаемая доходность, как следует из формулы 12.1, представляет собой средневзвешенную величину. Однако в реальной действительности она имеет определенный разброс значений вокруг средней ее величины, что связано с рыночным характером поведения многих факторов. Это обстоятельство послужило основой для применения теории вероятностей и математической статистики при обосновании кривой распределения, имеющей форму колокола и названной нормальным распределением. Использование полученного нормального распределения при аппроксимации данных, описывающих доходность диверсифицированных портфелей, позволяет анализировать все отклонения, имеющие место и лежащие за пределами средней величины ожидаемой доходности. Полученное при этом отклонение от средней величины ожидаемого дохода дает основание инвестору для ожидания как положительных эмоций, так и, возможно, отрицательных. К положительным свойствам предсказанного прогноза о доходности диверсифицированного портфеля следует отнести то, что средняя доходность портфеля может возрасти на некоторую величину, равную названному ранее стандартному отклонению. К отрицательным результатам интерпретации полученного прогноза с одинаковой доверительной вероятностью следует отнести то, что средняя полученная доходность портфеля может уменьшиться точно на такую же величину, что и при положительном прогнозе, равную стандартному отклонению. Понятно, что, руководствуясь интерпретацией полученного прогноза о возможной доходности сформированного инвестиционного портфеля, рисковый инвестор будет рассчитывать на получение максимальной доходности, равной средней доходности плюс стандартное отклонение, в то время как инвестор, не желающий рисковать, будет оценивать ожидаемую доходность из расчета: среднее значение доходности минус ее стандартное отклонение. Таким образом, ожидаемая доходность служит своего рода мерой потенциального вознаграждения, связанного с риском. Стандартное отклонение при этом может рассматриваться как мера риска. Чем больше его значение, тем больше риск. Стандартное отклонение портфеля, состоящее, к примеру, из 2 ценных бумаг, рассчитывается по следующей формуле: 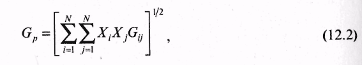 где Gij — это ковариация доходностей ценных бумаг iи j. Стандартное отклонение портфеля, состоящего из двух активов, можно рассчитать также по формуле: где Gp — стандартное отклонение. Ковариация — это статистическая мера взаимодействия двух случайных переменных, в качестве которых в нашем случае выступают доходности двух ценных бумаг i и j. Экономический смысл положительного взаимодействия состоит в том, что рост ожидаемой доходности одной ценной бумаги влечет за собой увеличение другой. Отрицательная ковариация показывает, что доходности двух ценных бумаг связаны между собой в противоположных направлениях. Например, рост ожидаемой доходности одной ценной бумаги сопровождается снижением ожидаемой доходности другой. Ожидаемое значение дохода портфеля будет во многом зависеть от суммы ожидаемых значений дохода отдельных ценных бумаг. Если же обнаруживаются определенные зависимости между курсовыми стоимостями отдельных бумаг, то при формировании портфеля это обстоятельство учитывается. При этом портфель, сформированный из акций компаний разных отраслей, обеспечивает надежность получения положительного результата. Ковариация весьма близка по смыслу к корреляции, под которой общепринято понимать взаимосвязь случайных переменных. Для измерения корреляции используется коэффициент корреляции, который всегда находится в интервале -1 и +1. Если он равен -1, то это означает полную отрицательную корреляцию, если +1 — полную положительную корреляцию. В большинстве случаев он находится между этими двумя экстремальными значениями. Например, взяв доходности двух ценных бумаг iи jза ряд месяцев, можно увидеть, что они между собой связаны. При этом по расчетам коэффициент корреляции равен -0,7. Это означает, что рост доходности iценной бумаги сопровождается снижением доходности; ценной бумаги. Численное значение коэффициента корреляции указывает на тесноту связи. Коэффициент корреляции нормирует ковариацию для облегчения сравнения с другими парами переменных. Ковариация двух случайных переменных равна корреляции между ними, умноженной на произведение их стандартных отклонений: где рij — коэффициент корреляции; Gi, Gj— стандартное отклонение соответственно i и jценной бумаги. Рассматривая, что такое ковариация и корреляция, весьма важно понимать, как производится двойное суммирование, используемое в уравнение 12.2. Здесь в определенной последовательности происходит анализ произведения весов двух ценных бумаг Xiи Xjи ковариации этих двух ценных бумаг. Следует отметить, что чаще всего в двойном суммировании используется ковариационная матрица, решение которой алгебраически можно представить в виде: 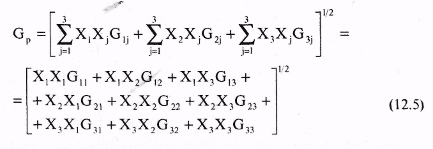 Любой ковариационной матрице соответствует корреляционная матрица, которая может быть определена по данным ковариационной матрицы и уравнению (12.4). С помощью данного уравнения можно показать, что корреляция между двумя ценными бумагами iи j равняется Gij / GiGj . Для выбора наиболее приемлемого для инвестора портфеля ценных бумаг можно использовать кривые безразличия. В данном случае эти кривые отражают предпочтения инвестора в графической форме, отвечая на вопросы о том, как инвестор ранжировал бы альтернативы. Предположения, сделанные относительно предпочтений, гарантируют, что инвесторы могут указать на предпочтение, отдаваемое одной из альтернатив или на отсутствие различия между ними. Если же рассматривать отношение инвестора к риску и доходности в графической форме, откладывая по горизонтальной оси риск, мерой которого является отклонение (Gp), апо вертикальной оси — вознаграждение, мерой которого является ожидаемая доходность (p), то можно получить семейство кривых безразличия. На рис. 12.2 представлен график кривых безразличия некоего гипотетического инвестора. Каждая кривая линия отображает одну кривую безразличия и представляет все комбинации портфелей, которые обеспечивают заданный уровень предпочтений инвестора. Например, инвесторы с кривой безразличия J2 будут считать портфели А и В равноценными, несмотря на то, что они имеют разные ожидаемые доходности и стандартные отклонения (14% и 21%). При этом ожидаемая доходность портфеля В составляет 15%, в то время как портфеля А — 10%. 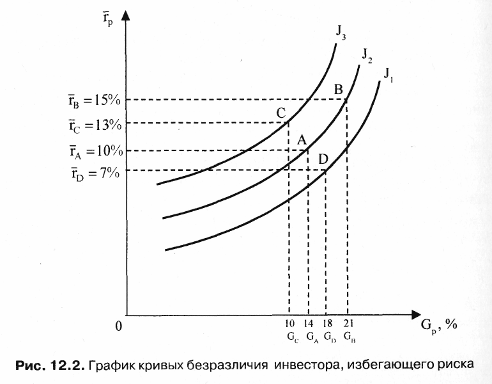 Как известно из экономической теории, кривые безразличия не могут пересекаться. Чтобы увидеть, почему это так, рассмотрим пересечение кривых безразличия, представленных на рис. 12.3. Здесь точка пересечения обозначена X. Поскольку портфель X расположен в точке пересечения кривых J1 J2, то инвестор не отдает предпочтение ни одному портфелю, расположенному на указанных кривых и отражающих различные уровни доходности и стандартного отклонения. 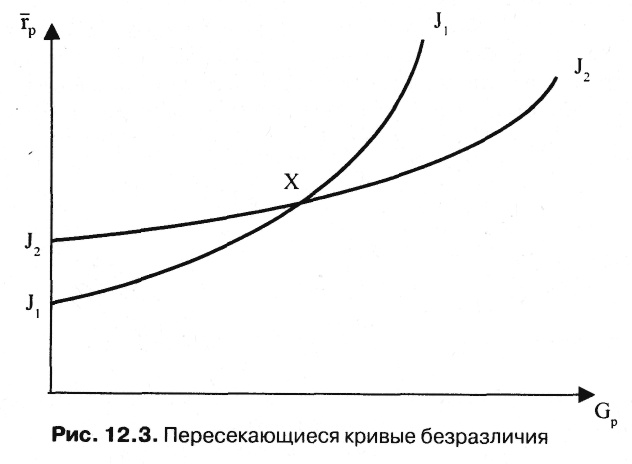 Располагая информацией об ожидаемой доходности и стандартных отклонениях возможных портфелей ценных бумаг, можно построить карту кривых безразличия, отражающих предпочтения инвесторов. Карта кривых безразличия — это способ описания предпочтений инвестора к возможному риску полностью или частично потерять вкладываемые в портфель Ценных бумаг деньги или получить максимальный доход. И здесь невольно вспоминается мрачноватая песенка Андрея Макаревича: Карты вечно тасуются, И в какой-нибудь раз Все вполне образуется, Но, наверно, без нас. Возвращаясь к кривым безразличия как к способу описания предпочтений инвестора, можно прийти к выводу, что если инвестор будет руководствоваться принципом избегания даже минимального риска, то естественно он ничего не получит от выбранного им портфеля ценных бумаг. И более того, вложенные в портфель деньги из-за возможной инфляции потеряют свою ценность. Аналогичным образом можно оправдать позицию инвестора, включившегося в азартную игру с целью заработать или прирастить вложенный капитал. Максимум, что может получить азартный игрок при хорошем раскладе, это высокую доходность вложенного капитала, а при неудачном стечении обстоятельств — определенные потери. Эти две возможные позиции консервативного и азартного инвестора можно представить в виде карт кривых, отражающих полезность вложений в те или иные инвестиционные портфели (рис. 12.4). 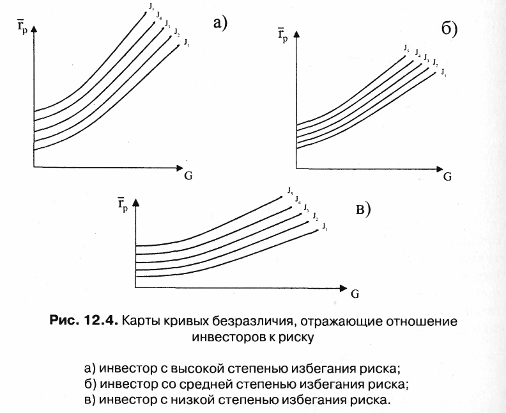 Каждая из указанных на рис. 12.4 позиций инвестора к риску характерна тем, что любое уменьшение им риска сказывается на сокращении доходности и стандартном отклонении каждого из пяти представленных портфелей. И поскольку портфель включает в себя набор различных бумаг, то вполне объяснимым является его зависимость от ожидаемой доходности и стандартного отклонения каждой ценной бумаги, входящей в портфель. Если же представить позиции азартного инвестора и инвестора, избегающего риска, то, как показано на рис. 12.5, кривые безразличия будут иметь иной характер. Азартный инвестор при принятии решения об инвестировании выберет портфель Е, который имеет наибольшую доходность. Инвестор же, нейтральный к риску, может выбрать любой портфель, поскольку их доходность не связана с риском (кривые безразличия представлены горизонтальными линиями). 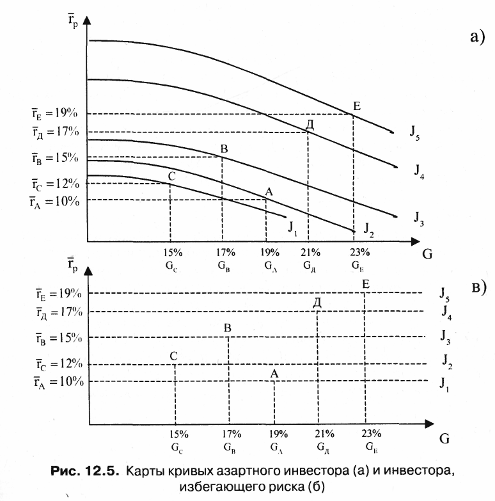 Таким образом, инвестору для принятия решения об инвестировании необходимо оценить альтернативные портфели с точки зрения их ожидаемых доходностей и стандартных отклонений, используя кривые безразличия. При этом наборе N цепных бумаг можно сформировать большое число портфелей для инвестирования. Согласно теории Марковица, для принятия решения о вложении средств инвестору не нужно проводить оценку всех портфелей, а достаточно рассмотреть лишь так называемое эффективное множество портфелей. Теорема об эффективном множестве (effecient set theorem) гласит: инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает:
Г. Марковиц показал, что на плоскости (G, ) график эффективного множества имеет вид (рис. 12.6), отражающий все возможные портфели из N ценных бумаг. 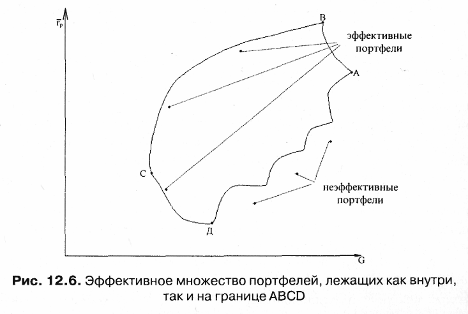 В зависимости от используемых ценных бумаг эффективное множество ABCD может быть смещено вправо, влево, вниз и вверх, а также быть больше площади, заключенной в ABCD. При этом не существует более рискованного портфеля, чем портфель А, поскольку ни одна из точек эффективного множества не будет лежать правее ее. Следовательно, множеством портфелей, обеспечивающих максимальную ожидаемую доходность при изменяющимся уровне риска, является часть верхней границы достижимого множества, расположенная между точками С и А. Кроме того, не существует портфеля, обеспечивающего меньшую ожидаемую доходность, чем портфель D, так как ни одна из точек достижимого множества не лежит ниже горизонтальной линии, проходящей через D. Если исходить из предположения, что границы допустимого эффективного множества портфелей лежат между точками С и А, В и D, то все остальные, т.е. лежащие за их пределами, свидетельствуют о неэффективности портфелей. Таким образом, эффективное множество содержит те портфели, которые обеспечивают и максимальную ожидаемую доходность при фиксированном уровне риска, и минимальный риск при заданном уровне доходности. При этом предполагается, что инвестор выберет оптимальный портфель из портфелей, составляющих эффективное множество. 12.3. Выбор состава оптимального портфеля ценных бумагДля того чтобы выбрать оптимальный портфель, инвестор должен нарисовать кривые безразличия, как это было показано ранее (рис. 12.5), а затем приступить к анализу всех портфелей, лежащих выше и левее всех остальных кривых безразличия с учетом ожидаемой доходности, стандартного отклонения и ковариации. Если иметь в портфеле несколько ценных бумаг, то это действительно просто сделать. Но когда формируется портфель, состоящий из сотен, а порой из тысячи ценных бумаг, то возникает проблема выбора из эффективного множества портфеля, представляющего собой оптимальную комбинацию доходности и стандартного отклонения, а также предпочтений инвестора относительно риска и доходности. Рассмотрим ряд моделей, используемых для формирования портфелей. Представим себе, что доходность обыкновенной акции за данный период времени связана с индексом РТС. В этом случае с ростом рыночного индекса, вероятно, будет расти и цена акции, а с падением рыночного индекса, вероятно, будет падать и цена акции. Эту взаимосвязь отражает рыночная модель (market model): где ri— доходность ценной бумаги iза данный период; rj— доходность на рыночный индекс jза этот же период; аij — коэффициент смещения; βij — коэффициент наклона; εij — случайная погрешность. Как следует из уравнения (12.6), чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги, εij = 0. Разность между действительным и ожидаемым значениями объясняется случайной погрешностью. Поэтому лишь только в ряде маловероятных случаев εij = 0. Это объясняет тот факт, что ценная бумага лежит на линии. Случайная погрешность позволяет сделать и другое предположение, что при данной доходности на рыночный индекс действительная доходность ценной бумаги обычно лежит вне прямой, задаваемой уравнением рыночной модели. При этом случайная погрешность, будучи случайной переменной с нулевым математическим ожиданием, всегда имеет стандартное отклонение относительно индекса рынка J. Если оценить зависимость между доходностью ценной бумаги и рыночным индексом без учета случайных погрешностей, то можно построить график рыночной модели определенной ценной бумаги. Например, с помощью формулы (12.6) можно получить следующее уравнение: где рыночный индекс (J) имеет доходность 10%, ожидаемая доходность ценной бумаги А составляет 14% (2% + 1,2% 10%). Если же доходность индекса будет равна -5%, то доходность ценной бумаги А ожидается равной -4% (2% + 1,2 (-5%)). Указанную зависимость можно показать на графике (рис. 12.7), где на вертикальной оси будет отложена доходность ценной бумаги (rA), ана горизонтальной оси доходность на рыночный индекс (rj). Наклон линии в рыночной модели ценной бумаги определяется чувствительностью ее к доходности на рыночный индекс. Коэффициент наклона в рыночной модели называют «бета»-коэффициентом, который рассчитывается по формуле: где σij— ковариация между доходностью акции iи доходностью акции рыночного индекса; σj —дисперсия доходности индекса или риск ценной бумаги. 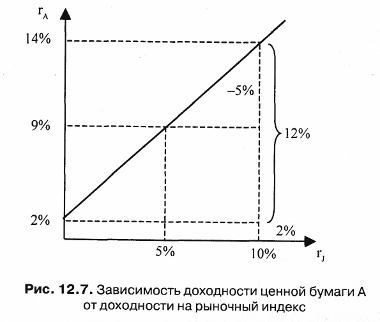 Если ценные бумаги имеют «бета»-коэффициент больше единицы, т.е. обладают большей изменчивостью, чем рыночный индекс, то их называют «агрессивными». И наоборот, ценные бумаги с коэффициентом меньше 1 называют «оборонительными». Общий риск ценной бумаги (σJ), измеряемый ее дисперсией (σJ2), состоит из двух частей: рыночного (или систематического) риска и собственного (или несистематического) риска. Таким образом, σJ2 можно выразить: где σJ2 — дисперсия доходности рыночного индекса; β2ijσJ2 — рыночный риск iценной бумаги; σε — собственный риск i ценной бумаги, мерой ε которого является дисперсия случайной погрешности (εij) из уравнения (12.6). Зная о весе и рыночном индексе каждой дисконтированной ценной бумаги в портфеле, а также о долях инвестирования в каждую бумагу, доходность портфеля можно рассчитать по формуле:  где хi = 1, 2, 3,..., N. Подставив значение ri(12.6) в указанное уравнение, получим: 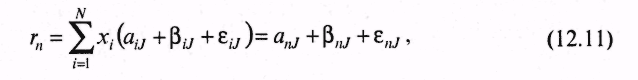 где  Из уравнений (12.11а и 12.11б) видно, что в качестве весов выступает доля каждого типа ценных бумаг в портфеле. Аналогичным образом определяется и случайная погрешность (12.11в). Общий риск портфеля, измеряемый дисперсией его доходности, можно определить по формуле: где  Если же предположить, что случайные отклонения доходности ценных бумаг являются некоррелируемыми, т.е. несвязанными между собой, то получим:  Таким образом, общий риск портфеля состоит из общего риска отдельных ценных бумаг, включающего в себя собственный риск (σ2εn), которого, по утверждению Г. Марковица, нельзя избежать, и рыночный риск: Собственный риск портфеля, или несистематический риск, связан с тем, что находящиеся в портфеле некоторые ценные бумаги могут как возрасти в цене, так и упасть. Следовательно, практически в любом портфеле будут иметь место ценные бумаги, которые могут одинаково влиять на его доходность. Сделав это предположение, можно показать, что если рассмотреть портфель ценных бумаг, в каждую из которых вложено одинаковое количество средств, то доля х составит 1/N, а уровень собственного риска на основании формулы (12.12в) соответственно будет равен: 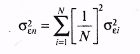 или 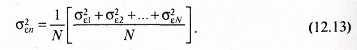 Понятно, что значение, находящееся внутри квадратных скобок в указанном уравнении, является средним собственным риском ценных бумаг, входящих в портфель. Если же увеличить число ценных бумаг (N), то сократится риск сформированного портфеля. На рис. 12.8 показана зависимость риска от диверсификации портфеля. Существует и другое положительное свойство диверсификации портфеля: оно приводит к усреднению рыночного риска путем изменения «бета»-коэффициента в зависимости от числа ценных бумаг, входящих в портфель. 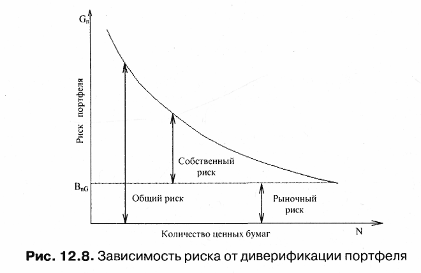 Подход, использующий рыночную модель, является приблизительным, как впрочем и все рассматриваемые в данном параграфе подходы. С помощью предложенного Г.Марковицем метода можно сформировать большое количество портфелей ценных бумаг, часть из которых будет относиться к эффективному множеству. Для выделения оптимальных портфелей, т.е. набора относительных долей акций и облигаций, которые могут принести их владельцу максимальный доход, Г.Марковиц использовал алгоритм квадратического программирования (метод критических линий). Нахождение оптимального портфеля с помощью указанного алгоритма включает в себя ряд процедур:
Процедура определения состава оптимального портфеля осуществляется с помощью графического нахождения инвестором уровня его доходности. По сути, если нанести на рис. 12.6 кривые безразличия, то можно найти такую точку О*, в которой доходность портфеля будет максимальна (рис. 12.9). Для этого следует нанести с помощью компьютера перпендикулярную к оси рлинию, а затем определить два «угловых» портфеля с ожидаемыми доходностями, находящихся в окрестности эффективного множества. 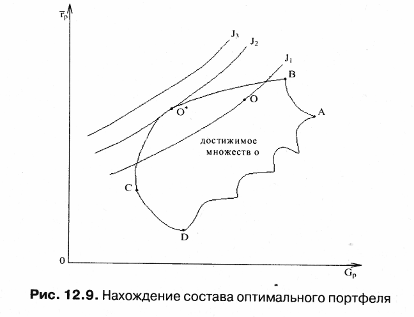 Ближайший «угловой» портфель будет расположен выше точки О, что соответствует большей ожидаемой доходности и ниже углового портфеля с соответственно меньшей ожидаемой доходностью. Если ожидаемую доходность оптимального портфеля обозначим как r* и ожидаемые доходности двух ближайших «угловых» портфелей обозначим как raи rbсоответственно, то состав оптимального портфеля может быть рассчитан по следующей формуле: Оптимальный портфель будет состоять из доли у, инвестированной в ближайший «угловой» портфель, находящийся выше оптимального, и доли, равной 1 -у, инвестированной в ближайший угловой портфель, расположенный ниже оптимального. Таким образом, предложенный выше Г. Марковицем подход ориентирован на то, что инвестор имеет некоторый начальный капитал, что позволяет ему полностью использовать его для формирования портфелей с определенным риском. При этом оптимальный портфель идентифицируется точкой касания кривых безразличия инвестора с эффективным множеством, характеризуемым не только определенной доходностью, но и риском. Рассмотрим ряд подходов к определению оптимальных портфелей ценных бумаг. Большой вклад в решение этой проблемы внесли Джеймс Тобин и Уильям Шарп. Они развили подход Марковица в ситуации, когда в экономике существует безрисковый актив с некоторой доходностью. Под безрисковым активом понимается актив, доходность от которого является определенной. И поскольку неопределенность конечной стоимости безрискового актива отсутствует, то, соответственно, стандартное отклонение для безрискового актива равно нулю. Если безрисковый актив имеет заранее известную доходность, то некие ценные бумаги, входящие в актив, должны обеспечивать инвестору фиксированный доход. В этой связи вряд ли корпоративные ценные бумаги могут принести инвестору фиксированный доход. В России, по-видимому, только один тип ценных бумаг можно было до недавнего времени отнести к безрисковым — это облигации федерального сберегательного займа. Инвестирование в безрисковый актив иногда называют безрисковым кредитованием. Дж. Тобин показал, что если р = (рi, ...рп) — некоторый портфель (рi— для i-го актива в портфеле), а f— безрисковый актив, то все портфели вида: лежат на прямой, проходящей через точки (0, rf) и (σр , p). Среди всех таких прямых нужно выбрать самую крутую (более крутая дает большую доходность при заданном риске р), т.е. ту, которая проходит через точку (0, rр ) и точку касания 0* к эффективной границе (рис. 12.10). 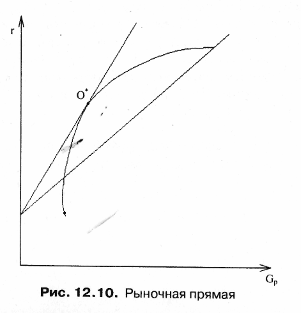 Это новая эффективная граница, полученная с учетом безрискового актива. Ее называют рыночной линией (CML, Capital Market Line), а точку называют рыночным портфелем (market portfolio). Смысл термина указал Уильям Шарп, который показал, что портфель можно вычислить на основе условия равенства спроса и предложения финансовых активов, рассматривая рынок в полном объеме как совокупность всех инвесторов и всех ценных бумаг (активов). В этом случае доля акций типа iв портфеле 0* просто равна доле всех акций типа iна рынке. Поэтому О* и называют рыночным портфелем. Алгоритм Марковица-Тобина дает решение задачи составления оптимального портфеля. Но в ситуации, когда нужно исследовать очень большое количество акций, он нереализуем из-за сложности вычислений (нужно обращать матрицу огромного размера). Эдвин Элтон, Мартин Грубер и Манфред Падберг предложили простой и изящный алгоритм вычисления портфеля 0* в предположении, что набор рассматриваемых активов можно описать моделью с одним индексом. В моделях с одним индексом рассматривается рыночный индекс I, характеризующий поведение фондового рынка в целом. На Западе очень популярен индекс Доу-Джонса, на нашем фондовом рынке — индекс РТС. Для рассматриваемого (базового) индекса I вводится естественное понятие доходности где PV0 — значение индекса в начале исследуемого периода; СI — значение индекса в конце рассматриваемого периода. Доходность riведет себя как случайная величина с определенным средним r1 и дисперсией σr2. Базовая доходность r1каким-то образом связана с доходностью финансовых активов rj, что измеряется ковариациями σij . В рамках модели с одним индексом предполагается, что доходности рассматриваемых активов представляются в виде  Следует подчеркнуть, что условия (4) и (5) — следствие выбора коэффициентов (1) и (2), а условие (6) — априорное допущение, которое нуждается в проверке в каждой конкретной рыночной ситуации. Алгоритмы Элтона-Грубера-Падберга и Марковица реализуют общий подход — при заданном у ровне ожидаемой доходности минимизировать риск. Стефан Росс в 1976 г. разработал другой подход к управлению портфелем. Его теория, известная как теория арбитражного ценообразования (APT, Arbitrage Pricing Theory), в некотором смысле менее сложна, чем рыночная теория Шарпа. В ее основе лежит предположение о том, что каждый инвестор стремится увеличить доходность своего портфеля, не увеличивая при этом возможный риск. Для достижения этой цели инвестор составляет арбитражный портфель. При формировании арбитражного портфеля используется модель с одним индексом. Арбитражным портфелем называют любой портфель А = (А1, А2,..., Аn) с условиями: 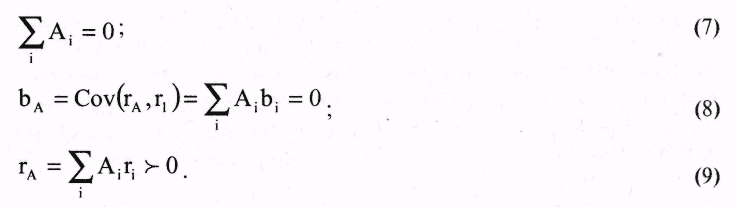 Условие (7) означает, что для составления портфеля А не требуется дополнительных ресурсов. Условие (8) означает, что арбитражный портфель не чувствителен к базовому фактору. Условие (9) означает, что ожидается положительная доходность портфеля А. Арбитражный портфель формируется таким образом, чтобы его риск был существенно меньше риска текущего портфеля. Еще предпочтительнее, чтобы риск арбитражного портфеля был близок к нулю: Допустим, что у нас ебть старый (текущий) портфель и мы сформировали некоторый арбитражный портфель А с условиями (7-10). Тогда мы строим новый текущий портфель: с компонентами Ожидаемая доходность этого портфеля равна: В силу свойства (9) она выше ожидаемой доходности старого портфеля р. Риск нового портфеля остался на прежнем уровне: Последнее значение следует из известного неравенства Такова суть подхода к управлению портфелем на основе арбитражной теории ценообразования. Надо сказать, что получение безрисковой прибыли путем использования разных цен на ценные бумаги, что собственно и называется арбитражем, является широко распространенной инвестиционной тактикой. Инвесторы стремятся получить доходы при каждой возможности: продавая ценные бумаги по высокой цене и одновременно приобретая такие же ценные бумаги по относительно низкой цене. Для реализации арбитражного подхода как правило используется факторный анализ курса ценных бумаг. При этом делается предположение о том, что можно увеличить доходность своего портфеля без увеличения риска. Однако существует ряд систематических факторов, влияющих на риск и доходность ценной бумаги, что серьезным образом препятствует широкому применению модели APT на практике. Рассмотрим модель с одним индексом применительно к условиям российского рынка. Возьмем в качестве базового (ведущего) фактора I индекс РТС. Чтобы представить (12.17), нужно знать параметры ri, r1, σi1, σr2, которые в реальных ситуациях никогда не известны. На практике вместо этих параметров используют их статистические оценки: 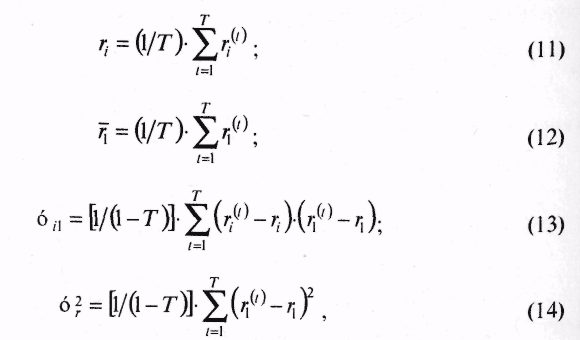 которые строятся на имеющемся материале где ri(t), r1(t) — доходность i-го актива (соответственно индекса I) за некоторый период С; Т— число периодов, взятых для построения оценок. Нормированные суммы (11) и (12) называются выборочными средними, сумма (12) — выборочной ковариацией, а сумма (13) — выборочной дисперсией. При определенных условиях оценки (11-14) с большой вероятностью (в силу известного в теории вероятностей закона больших чисел) близки к соответствующим оцениваемым характеристикам ri, r1, σi1, σr2. С помощью оценок (11-14) строятся оценки:  соответствующих величин ri(t) и r1(t). Наконец, с помощью оценок (15) и (16) и наблюдений вычисляются оценки остатков которые получаются из уравнения и которые представляет собой статистический аналог исходного уравнения. Остатки (17) представляют основной интерес при исследовании модели с одним индексом. Нетрудно проверить, что для них выполняются соотношения: 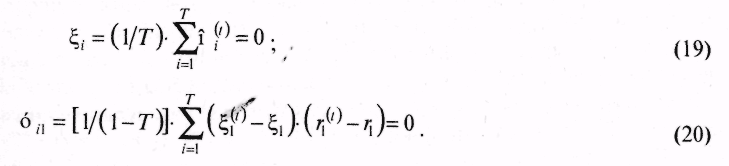 Это статистические аналоги соотношений (4) и (5), лишний раз подтверждающие теоретическую неизбежность выполнения свойств (4) и (5). С выполнением свойства (6) для ковариации дело обстоит совершенно иначе. Статистической оценкой для этой величины является выборочная ковариация поведение которой характеризует поведение теоретической ковариации (21). Результаты апробации указанного подхода показали, что применение модели с одним индексом требует серьезной проработки каждого конкретнрго случая. Множество оптимальных по Марковицу-Тобину портфелей ведет себя достаточно стабильно и меняется скачкообразно только в моменты, когда котировки некоторых ценных бумаг резко «прыгают». В эти моменты следует пересматривать структуру портфеля. Изменение в широком диапазоне безрисковой процентной ставки не влияет на структуру оптимального по Марковицу-Тобину портфеля. Поэтому при расчетах можно не менять (в соответствующем диапазоне) доходность ценных бумаг. При расчете оптимального портфеля в условиях российского фондового рынка предпочтительнее пользоваться моделью Г. Марковица и ориентироваться на стратегию формирования арбитражного портфеля. При этом нельзя игнорировать того, о чем писал известный нобелевский лауреат 1976 г. в области экономики, Милтон Фридмен: «Что касается "предположений" какой-либо теории, то уместным является не вопрос об их "реалистичности", которой они никогда не обладают, а о том, насколько хорошей аппроксимации рассматриваемого явления они позволяют добиться, и ответом на это является демонстрация того, как работает теория, дает ли она достаточно точные предсказания» (Milton Friedmen. Essays in the Theory of Positive Economics. — Chicago: Univesity Chicago Press, 1953. P.15). 12.4. Формирование первичного портфеля облигацийФормирование портфеля государственных облигаций осуществляется путем покупки облигаций на аукционах, при первичном размещении или на вторичных торгах. Для покупки облигаций инвестор составляет заявку-поручение дилеру, где указывает возможные цены покупки облигаций, количество бумаг и сумму денежных средств, которую предполагает затратить на покупку облигаций. В заявке на аукцион указываются два вида покупок: конкурентные и неконкурентные. Неконкурентные заявки выполняются по средневзвешенной цене аукциона, поскольку инвестор не может изменить цену. Облигации, включенные в неконкурентные заявки, оговариваются заранее в документах, публикуемых в официальных финансовых изданиях за 7 дней до проведения аукциона. Доля неконкурентных заявок как правило составляет 15-30% от общего объема средств, размещенных на аукционе. Конкурентные заявки удовлетворяются по цене, которую указывает инвестор, но не ниже цены отсечения. Цена отсечения рассчитывается организаторами аукциона на основе анализа всех участвующих в аукционе заявок. При этом инвестору важно указать цену покупки, которую он может установить путем изучения спроса. Если же инвестор укажет в заявке неприемлемую для организаторов аукциона цену, то заявка не будет удовлетворена. Необходимо отметить, что достоверный прогноз цены обеспечения весьма сложно получить. Кроме факторов спроса и предложения на цену влияют экономическая и политическая обстановка в стране, которые в каждом отрезке времени действуют по-разному, что в свою очередь отрицательно сказывается на точности прогноза. При всех факторах неопределенности цены отсечения существуют ее предельные границы, которые базируются на представлениях инвестора о приемлемой для него норме доходности по инвестированию средств с учетом риска и альтернативных вариантов вложения капитала. В качестве отправной точки отсчета цены облигации является их стоимость на рынке и возможность альтернативного инвестирования, включая помещение средств в банк на депозит по определенной процентной ставке, превышающей иные варианты вложения средств. При этом будущая сумма, которую инвестор предполагает получить, составляет: где C(t) — будущая сумма получения; PV — текущая сумма вложения; rа — ставка доходности, % (ставка дисконтирования). Полученная сумма может быть увеличена из-за инфляции, которая измеряется индексом цен определенной группы товаров. Количественный уровень инфляции можно определить по следующей формуле:  где ΔС — величина, на которую надо увеличить ожидаемую сумму с тем, чтобы не уменьшить ее покупательную способность. Индекс инфляции Jiрассчитывается как: Ji = 1 + τi. Следовательно, для сохранения эффективности инвестиций необходимо ввести в указанную выше формулу индекс инфляции. Тогда: Аналогично может быть дополнительно учтен риск: где τp — дополнительная ставка, компенсирующая риск. Поскольку при покупке облигации инвестор затрачивает сумму PV, а при погашении получает номинальную цену облигации Ni, то выражение (12.20) можно записать в следующем виде откуда цена облигации за выбранный период времени равна  где ra, τi — соответственно ставка альтернативного вложения, инфляции. Ставку дисконтирования Еdможно рассчитывать из уравнения: В публикуемых официальных финансовых изданиях в качестве расчетного периода, как правило, рассматриваются месяц, квартал, год, что предопределяет расчетную ставку дисконтирования и реальную цену облигации, т.е. ту цену, которую инвестор готов заплатить на аукционе. Цена облигации при неизменных во времени ставках рассчитывается по формуле:  где Рi — цена iоблигации; Ni — номинал i облигации; rа — ставка дисконтирования; п — показатель кратности срока обращения облигации относительно базового периода где Tg — период обращения облигации до погашения; 30 — месячный период. где t0 — дата аукциона; tR — дата погашения облигации. Если изменяются условия инвестирования, то для каждого периода времени вложений, к примеру месяца, можно отдельно ввести ставки дисконтирования. Тогда цена облигации может быть определена по формуле: 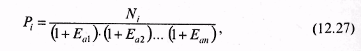 где Eal,... Еan — ставки дисконтирования каждого месяца инвестиционного периода. Зная возможную цену облигации, инвестор может указать ее в заявке на аукцион. Цену облигации для оформления заявки на аукцион можно определить и на основе анализа конъюнктуры рынка. Для этого по результатам вторичных торгов на фондовых биржах, предшествующих дню аукциона, определяется эффективная доходность De всех выпусков, обращающихся на рынке. Эффективная доходность рассчитывается на основе средневзвешенных цен облигаций на торгах. Затем выбираются выпуски, имеющие даты погашения, близкие к дате погашения нового (аукционного) выпуска. Из отобранных выпусков формируется ряд эффективных доходностей {De} и выбирается максимальная доходность этого ряда De max. Полученная величина De maxпринимается в качестве исходного показателя для расчета аукционных цен нового выпуска. При этом в качестве базового периода принимается год (360 дней). Эффективная доходность облигаций ряда выпусков определяется по следующей формуле: где Pcj — средневзвешенная цена на вторичных торгах, предшествующих аукциону; Ti — период до погашения выпуска i; Ее— эффективная ставка операции для выпуска. Средневзвешенная цена облигации Pajнового выпуска; определяется по формуле: 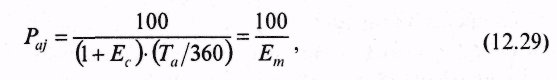 где Тa— период обращения выпуска j; Em — комплексный показатель. Краткие выводы
Рекомендуемая литература
ЧАСТЬ 2. ИНВЕСТИЦИОННЫЕ ПРОЕКТЫРАЗДЕЛ 3. ТЕХНИКО-ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ ИНВЕСТИЦИОННОГО ПРОЕКТА |
