Статья. Удк моделирование расчетной схемы составной балки, расположенной на упругом основании на основе программы AutodeskRobot Structural Analysis Professional
 Скачать 210.31 Kb. Скачать 210.31 Kb.
|
|
УДК Моделирование расчетной схемы составной балки, расположенной на упругом основании на основе программы AutodeskRobot Structural Analysis Professional С.Ю. Сурненков, Л.Ю. Ступишин ЮЗГУ 305040, г. Курск, ул. 50 лет Октября, д. 94. stustu19@bk.ru В настоящей статье анализируются результаты аналитического и программного методов решения полубесконечной составной балки, расположенной на винклеровском упругом основании и загруженной в начальном сечении вертикальной нагрузкой. Ключевые слова: составная балка, теория А.Р. Ржаницына, бесконечно длинная балка, основание Винклера, прогиб балки, внутренние усилия Key words: composite beam, the theory by A. R. Rzhanitsyn, infinite beam, Winkler elastic foundation, deflection of beam, internal forces Различные инженерные сооружения и конструкции, расчётная схема которых представлена в виде балки на упругом основании, находят широкое применение в строительной практике. К ним относятся, например, несущие конструкции многоэтажных зданий, автомобильные дороги, рамные каркасы, сквозные и пустотелые железобетонные балки и плиты, составные металлические колонны и балки и др. Рассмотрим полубесконечную балку, состоящую из двух горизонтальных брусьев, соединенных между собой вертикальными стойкамии, расположенную на упругом винклеровском основании (рис.1). Балка находится под действием заданной вертикальной нагрузки. 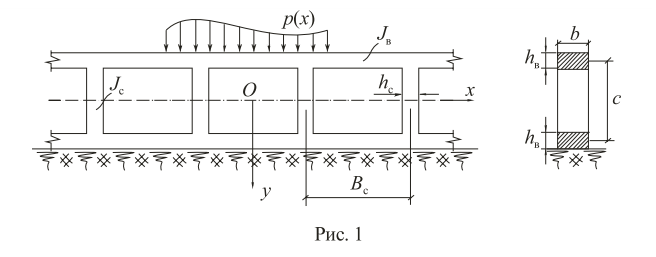 Аналитический метод Балка, состоящая из двух горизонтальных брусьев, соединенных между собой вертикальными стойками, расположена на упругом винклеровском основании (рис.1) и находится под действием заданной вертикальной нагрузки. Для описания работы балки под нагрузкой воспользуемся теорией составных стержней А.Р.Ржаницына [1], с позиций которой рассматриваемая балка представляет собой двухветьевой составной стержень (рис.2.а). Поведение такого стержня описывается следующим дифференциальным уравнением: 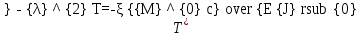 (1) (1)Здесь Т — сдвигающее усилие, передающееся на горизонтальные ветви от вертикальных стоек; М0— изгибающий момент, возникающий от вертикальной нагрузки в основной системе, лишенной связей сдвига (рис.2.б); с — расстояние между центрами тяжести ветвей; 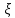 — коэффициент жесткости на сдвиг; — коэффициент жесткости на сдвиг; 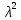 — коэффициент, определяемый по формуле: — коэффициент, определяемый по формуле: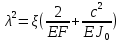 (2) (2)где F — площадь поперечного сечения каждой из ветвей; 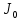 — суммарный момент инерции сечения ветвей. — суммарный момент инерции сечения ветвей. В рассмотренном случае эти величины равны: 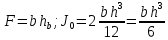 Считая, что вертикальные стойки расположены регулярно (Вc = const), жестко связаны с горизонтальными брусьями и выполнены из того же материала, для коэффициента жесткости на сдвиг 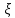 можно получить следующую формулу [1]: можно получить следующую формулу [1]: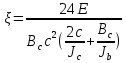 (3) (3)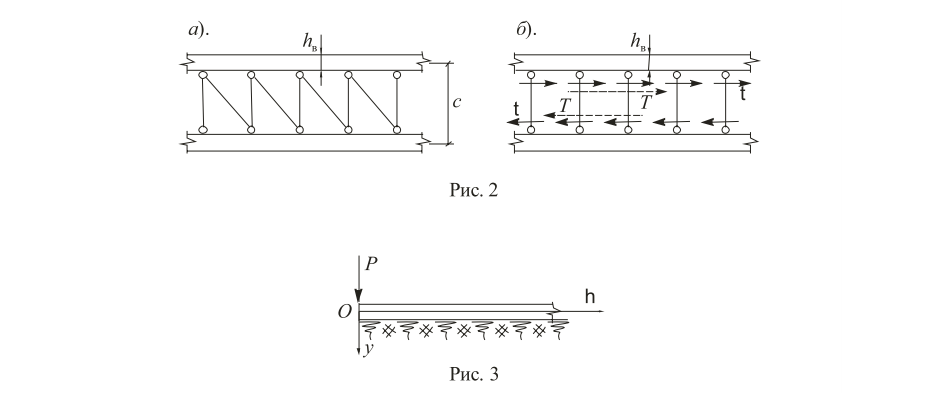 Изгибающий момент М0 вызывает искривление осей, составляющих основную систему стержней, по одинаковым кривым v0(x). В связи с тем, что рассматриваемая балка расположена на поверхности винклеровского упругого основания, эти кривые могут быть найдены из решения дифференциального уравнения: 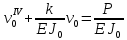 (4) (4)где k=bk0 , а k0— коэффициент постели упругого основания. Рассмотрим полубесконечную балку (рис.3), находящуюся под действием силы Р , приложенной в начале координат. Введем безразмерную переменную 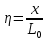 , где , где 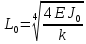 , и представим решение уравнения (4) в следующем виде [2]: , и представим решение уравнения (4) в следующем виде [2]: 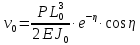 (5) (5)Используя справедливое при малых прогибах соотношение 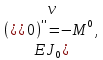 (6) (6)для изгибающего момента, входящего в правую часть уравнения (1), можно получить выражение: 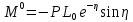 (7) (7)Общее дифференциальное уравнение (1) для бесконечно составного стержня, загруженного сосредоточенной силой Р, может быть теперь получена в виде: 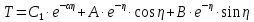 (8) (8)где 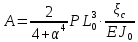 , , 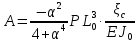 , , 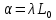 (9) (9)а С1 – постоянная интегрирования, подлежащая определению из граничного условия: при 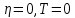 . .Раскрывая это условие, получим: 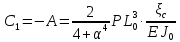 , после чего выражение (8) примет окончательную форму: , после чего выражение (8) примет окончательную форму: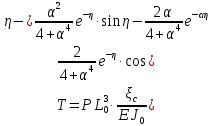 (10) (10)Заметив, что полный изгибающий момент в составной балке определяется выражением 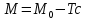 и подставив сюда формулы (7) и (10), найдём: и подставив сюда формулы (7) и (10), найдём: 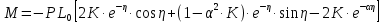 . (11) . (11)Здесь 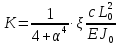 . .Используя зависимость, аналогичную (6), и дважды интегрируя выражение (11), для функции прогибов составной балки, получим формулу: 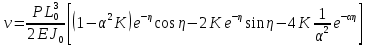 (12) (12)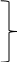 Однократное дифференцирование выражений (10), (11) и (12) позволяет получить формулы соответственно для скалывающих напряжений Однократное дифференцирование выражений (10), (11) и (12) позволяет получить формулы соответственно для скалывающих напряжений 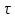 , поперечных сил Q и углов поворота , поперечных сил Q и углов поворота 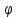 составной балки: составной балки: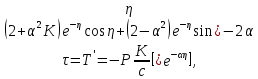  (13) 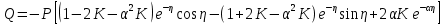 , ,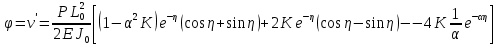 . .Анализируя полученные выражения для перемещений и расчётных усилий бесконечно длинной составной балки, можно видеть, что при ξ→ 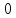 мы приходим к формулам (5) и (7), описывающим работу балки, лишённой связей сдвига, а при мы приходим к формулам (5) и (7), описывающим работу балки, лишённой связей сдвига, а при 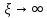 − к формулам, характеризующим поведение монолитной балки, состоящей из двух горизонтальных ветвей: − к формулам, характеризующим поведение монолитной балки, состоящей из двух горизонтальных ветвей: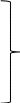 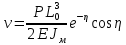 , , (14) 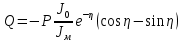 , ,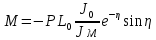 , ,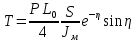 Решение с помощью программного комплекса Autodesk Robot Structural Analysis Professional Проектируем в программе исходную расчётную схему (схема 1), с единичной нагрузкой Р 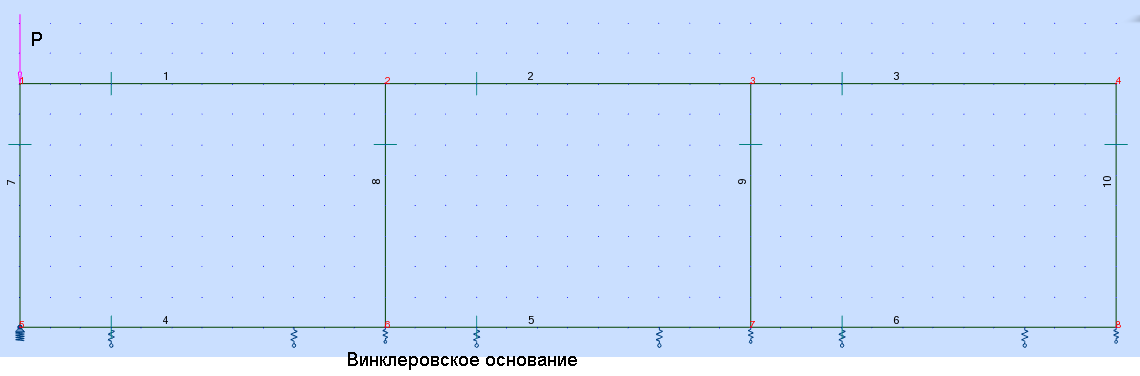 Балка, состоящая из двух горизонтальных брусьев, соединенных между собой вертикальными стойкамии, расположенная на упругом винклеровском основании (схема 1) Ведём расчёт и сравниваем единичные эпюры моментов, полученные от аналитического и машинного метода решения (Рис. 4)  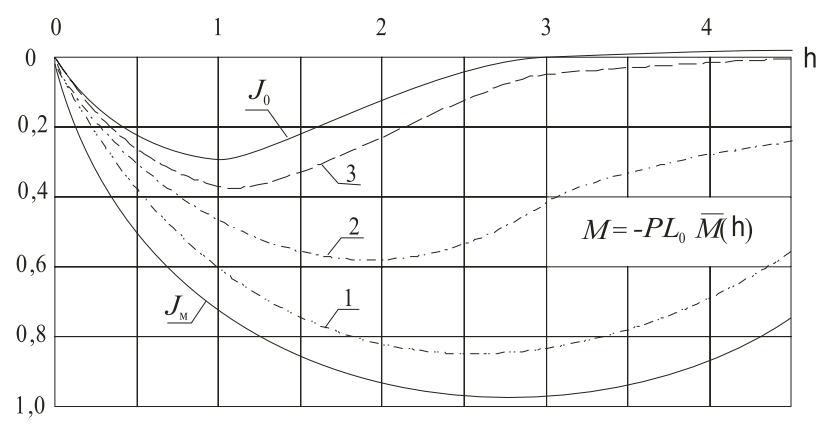 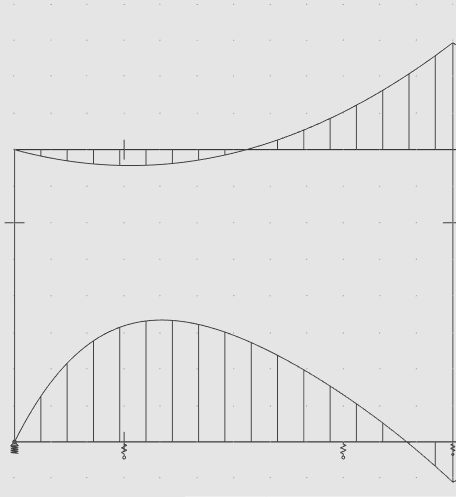 Эпюры моментов от единичной нагрузки Р (Рис. 4) Анализируя полученные результаты, делаем вывод, что эпюры полученные при решении задачи выше предложенными методами имеют весьма неплохую сходимость. Это позволяет гораздо ускорить подобные расчёты без значительной потери точности. Ссылки на печатные источники: Ржанпцын А.Р. Составные стержни и пластинки. Москва, Стройиздат, 1986. Леонтьев Н.Н.‚ Леонтьев А.Н., Анохин Н.Н.. Соболев Д.Н.. Основы теории балок и плит на деформируемом основании. Москва, МИСИ, 1982. Атаров Н.М.,. Леонтьев А.Н, Леонтьева И.Г. Изгиб составной балки, расположенной на упругом основании, Москва, Вестник, 2011. Варвак П.М. Метод конечных элементов. Киев, 1981. Цвей А.Ю. Балки и плиты на упругом основании. Москва, МАДИ. 2014. Власов В.З., Леонтьев Н.Н. Балки, плиты и оболочки на упругом основании, Москва, 1960. |
