Контрольная работа №1 Расчет линейной электрической цепи постоянного тока. Уфимский государственный авиационный технический университет
 Скачать 430.47 Kb. Скачать 430.47 Kb.
|
 Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра теоретических основ электротехники Контрольная работа №1 Расчет линейной электрической цепи постоянного тока Код;431159-вариант №1 Выполнил: студент гр. Проверил: Преподаватель: Уфа 2017 Начальные условия: 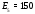 В; В;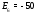 В; В;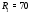 Ом; Ом; 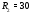 Ом; Ом;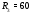 Ом; Ом; 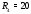 Ом; Ом;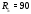 Ом; Ом; 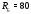 Ом; Ом;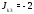 А; А; 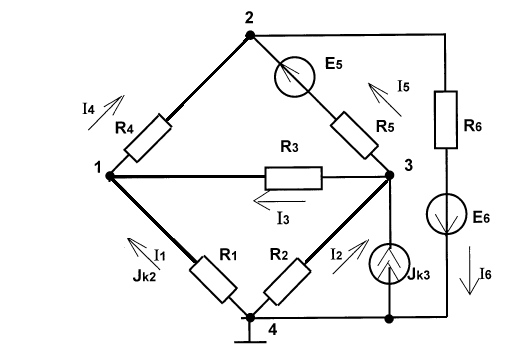 Рисунок 1. - Исходная схема Задания: 1. Определить все токи методом контурных токов. 2. Определить все токи методом узловых потенциалов, приняв потенциал 4-го узла равным нулю 3. Произвести проверку по законам Кирхгофа. 4. Составить баланс мощностей. 5. Определить ток 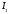 методом эквивалентного генератора. методом эквивалентного генератора.6. Начертить в масштабе потенциальную диаграмму для любого контура, включающего в себя две ЭДС. 1. Расчет цепи методом контурных токов Зададим произвольно направление токов в ветвях схемы (Рисунок 2). 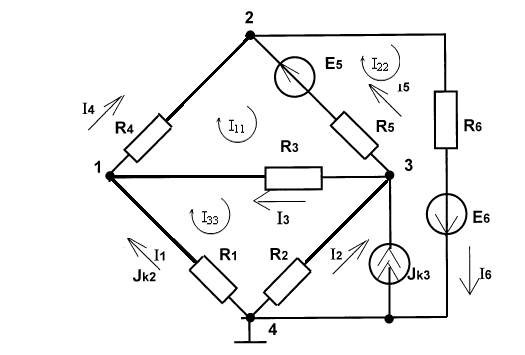 Рисунок 2. - Схема с произвольно выбранными направлениями токов Число ветвей схемы в=7 Число ветвей схемы, содержащих источник тока 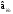 =1 =1Число узлов y=4 Составим линейно независимые уравнения по первому и второму закону Кирхгофа: 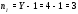 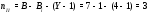 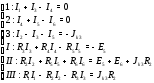 Зададим произвольное направление контурных токов:  Рисунок 3. - Схема с произвольно выбранными направлениями контурных токов Для каждого контура составим уравнения по второму закону Кирхгофа: 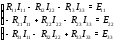 Выразим искомые токи через контурные токи: 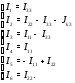 Определим собственные и взаимные сопротивления: 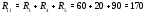 Ом Ом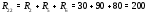 Ом Ом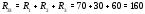 Ом Ом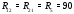 Ом Ом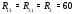 Ом Ом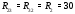 Ом ОмОпределим контурные ЭДС: 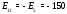 В В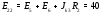 В В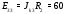 В ВСистема уравнений выглядит следующим образом: 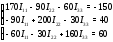 Решая данную систему уравнений, получаем следующие контурные токи: 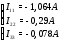 Находим искомые токи: 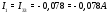 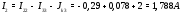 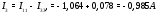 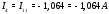 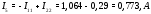 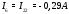 2. Расчет цепи методом узловых потенциалов Обозначим потенциалы в узлах 1, 2, 3,4 как 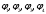 . .  Рисунок 3. - Схема с обозначенными потенциалами в узлах Приравняем потенциал узла 4 к нулю 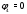 Составим систему уравнений для нахождения потенциалов: 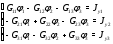 Определим взаимную и собственную проводимости: 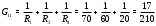 См; См; 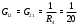 См; См;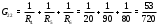 См; См; 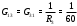 См; См;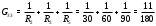 См; См; 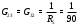 См. См.Найдем узловые токи: 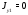 A; A;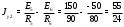 A; A;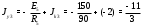 A; A;Подставив значения, получим: 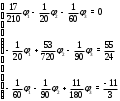 Решая систему уравнений, получим: 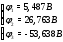 Выразим искомые токи через потенциалы 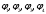 : :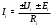 Надем значения токов: 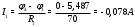 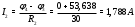 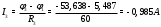 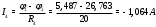 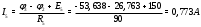 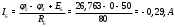 3. Составим уравнения по законам Кирхгофа: Определяем количество необходимых уравнений по первому и второму закону Кирхгофа: 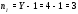 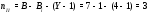 Запишем систему уравнений на основании законов Кирхгофа: 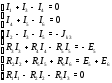 Проведем проверку по законам Кирхгофа: ПЕРВЫЙ ЗАКОН: Алгебраическая сумма токов сходящихся в узле равна нулю Узел 1: 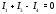 , ,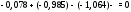 Узел 2: 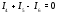 , ,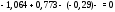 Узел 3: 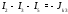 , ,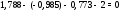 ВТОРОЙ ЗАКОН: Алгебраическая сумма падений напряжений вдоль замкнутого контура равна алгебраической сумме ЭДС, действующей в том же контуре. 1 контур: 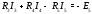 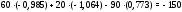 2 контур: 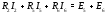 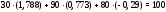 3 контур: 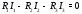 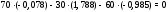 Законы Кирхгофа выполняются, следовательно токи найдены верно. 4. Баланс мощностей. Составим баланс мощностей в исходной схеме с источником тока, вычислив суммарную мощность источников и суммарную мощность приемников. 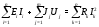 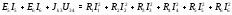 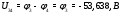 Суммарная мощность источников: 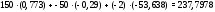 Вт; Вт;Суммарная мощность приемников: 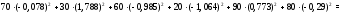 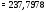 Вт; Вт;Допускается расхождения баланса активных мощностей 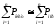 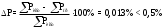 Баланс мощностей сходится, значит, расчет токов произведен верно. 5. Расчет тока 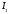 методом эквивалентного генератора. методом эквивалентного генератора.5.1 Рассчитаем сопротивление генератора: Определим входное сопротивление всей схемы по отношению к зажимам 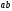 при закороченных источниках ЭДС и разомкнутой ветви с источником тока: при закороченных источниках ЭДС и разомкнутой ветви с источником тока: 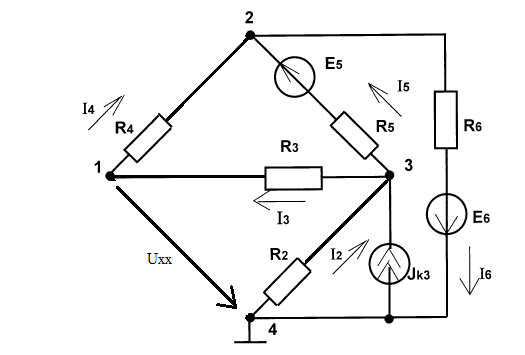 Рисунок 4. - Ветвь 1 разомкнута Заменим данную схему, преобразовав соединение сопротивлений треугольник 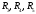 на эквивалентное соединение звезда : на эквивалентное соединение звезда : 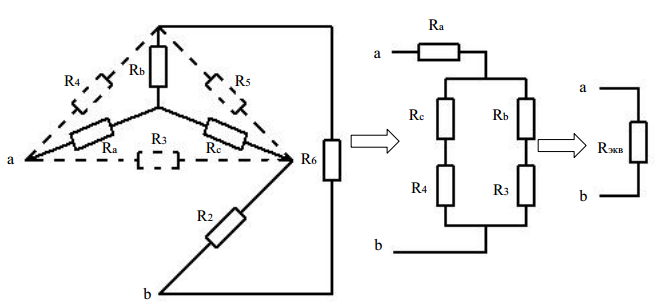 Рисунок 5. - Преобразование схемы для определения  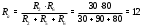 Ом; Ом;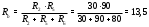 Ом; Ом;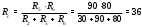 Ом; Ом;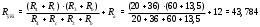 Ом; Ом;5.2 Расчет напряжения холостого хода 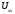 . .Разомкнем ветвь и определим напряжение 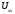 на зажимах разомкнутой ветви на зажимах разомкнутой ветви 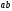 . .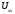 можно представить в следующем виде: можно представить в следующем виде: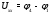 Принимая 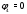 получим: получим: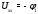 Найдем неизвестное значение 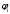 методом узловых потенциалов. методом узловых потенциалов.Составим систему уравнений для нахождения потенциалов: 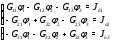 Определим взаимную и собственную проводимости: 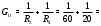 См; См; 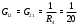 См; См;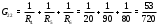 См; См; 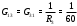 См; См;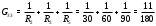 См; См; 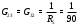 См. См.Найдем узловые токи: 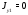 A; A;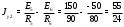 A; A;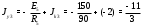 A; A;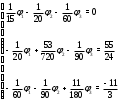 Решая данную систему уравнений, получим: 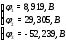 Определим напряжение 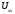 : :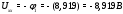 Найдем искомый ток 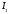 по закому ома: по закому ома: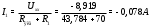 Как мы видим, значение тока в первой цепи, полученное по методу эквивалентного генератора, практически совпадает с полученным другими методами. 6. Построим потенциальную диаграмму для контура, содержащего два источника ЭДС. 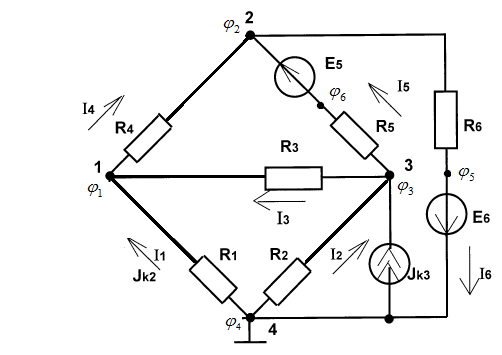 Рисунок 6. - Схема с обозначенными потенциалами в узлах Рассчитаем значение потенциала во всех точках контура: 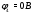 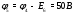 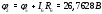 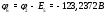 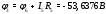 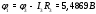 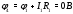 По полученным данным построим потенциальную диаграмму: 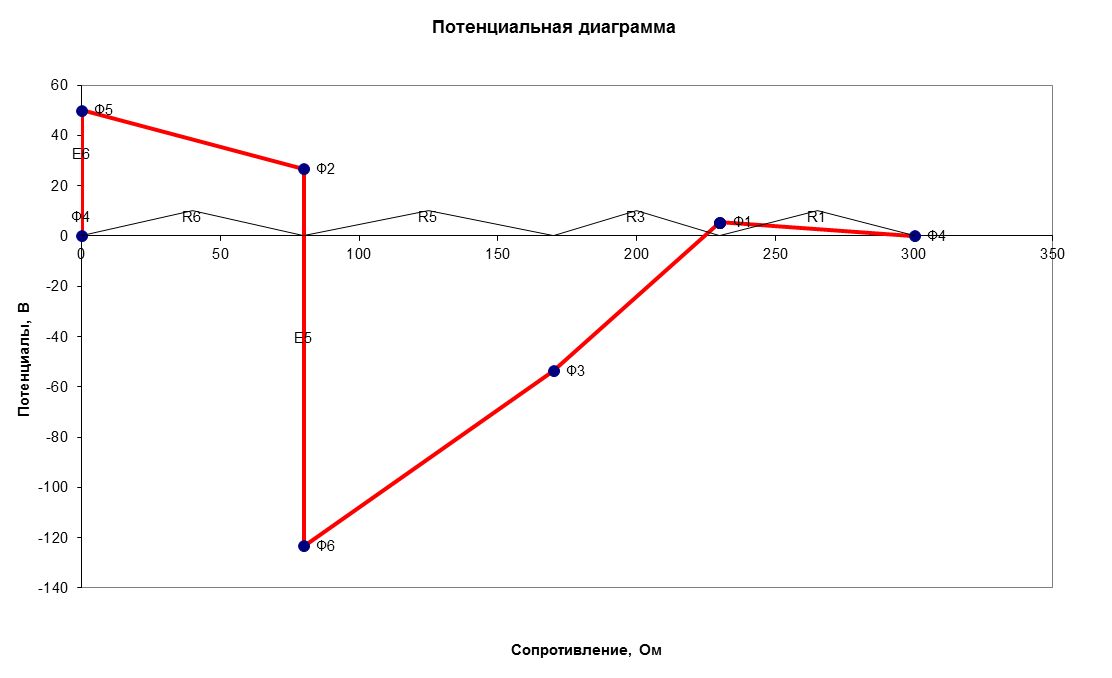 Рисунок 7. - Потенциальная диаграмма Проверка ответов: Баланс мощностей P:237,7978 Входное сопротивление схемы со стороны зажимов первой ветви Rвх:43,7838 ДКТ:2947000 - Это есть определитель матрицы.(Детерминант при расчете методом контурных токов) ДУП:0,000162423 - Это есть определитель матрицы.(Детерминант при расчете методом узловых потенциалов) Напряжение холостого хода на первой ветви Uxx:-8,919 - Это есть сумма 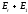 Потенциал Фи1:5,4869 Потенциал Фи2:26,7628 Потенциал Фи3:-53,6376 Ток I1:-0,0784 Ток I2:1,7879 Ток I3:-0,9854 Ток I4:-1,0638 Ток I5:0,7733 Ток I6:-0,2905 |
