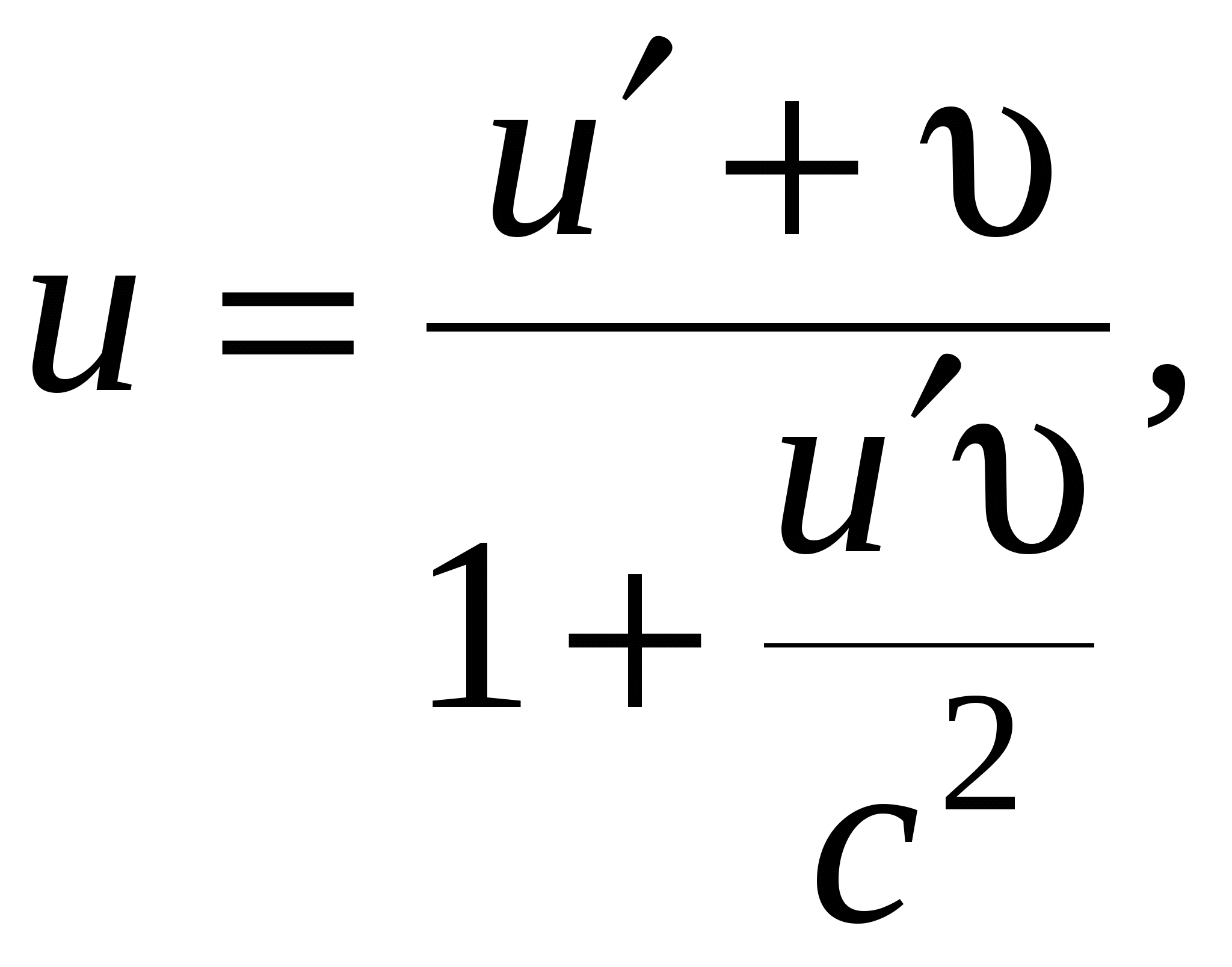|
|
Сборник задач по механике. Уфимский государственный авиационный технический университет
M=Fl,
где l – кратчайшее расстояние от прямой, вдоль которой действует сила, до оси вращения.
Моментом инерции материальной точки относительно какой-нибудь оси вращения называется величина
J=mr2,
где m – масса материальной точки и r – ее расстояние до оси вращения.
Моментом инерции твердого тела относительно его оси вращения
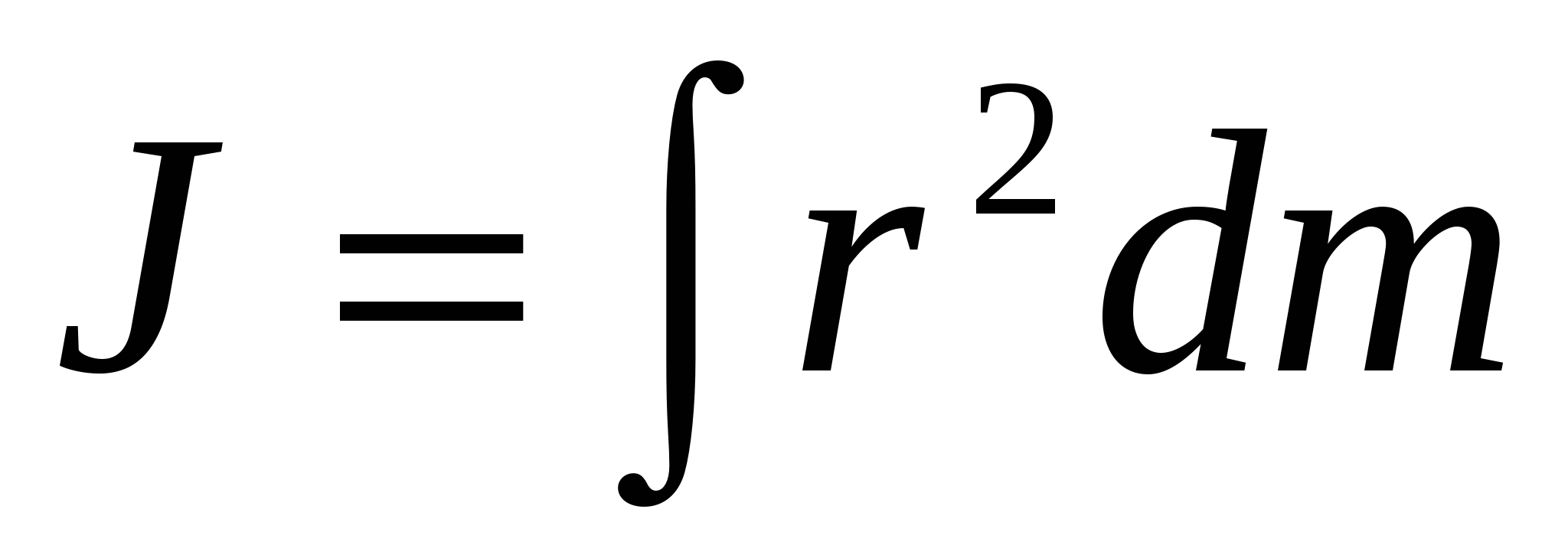 , ,
где интегрирование должно быть распределено навесь объем тела. Производя интегрирование можно получить момент инерции тела любой формы.
Момент инерции сплошного однородного цилиндра (диска) относительно оси цилиндра
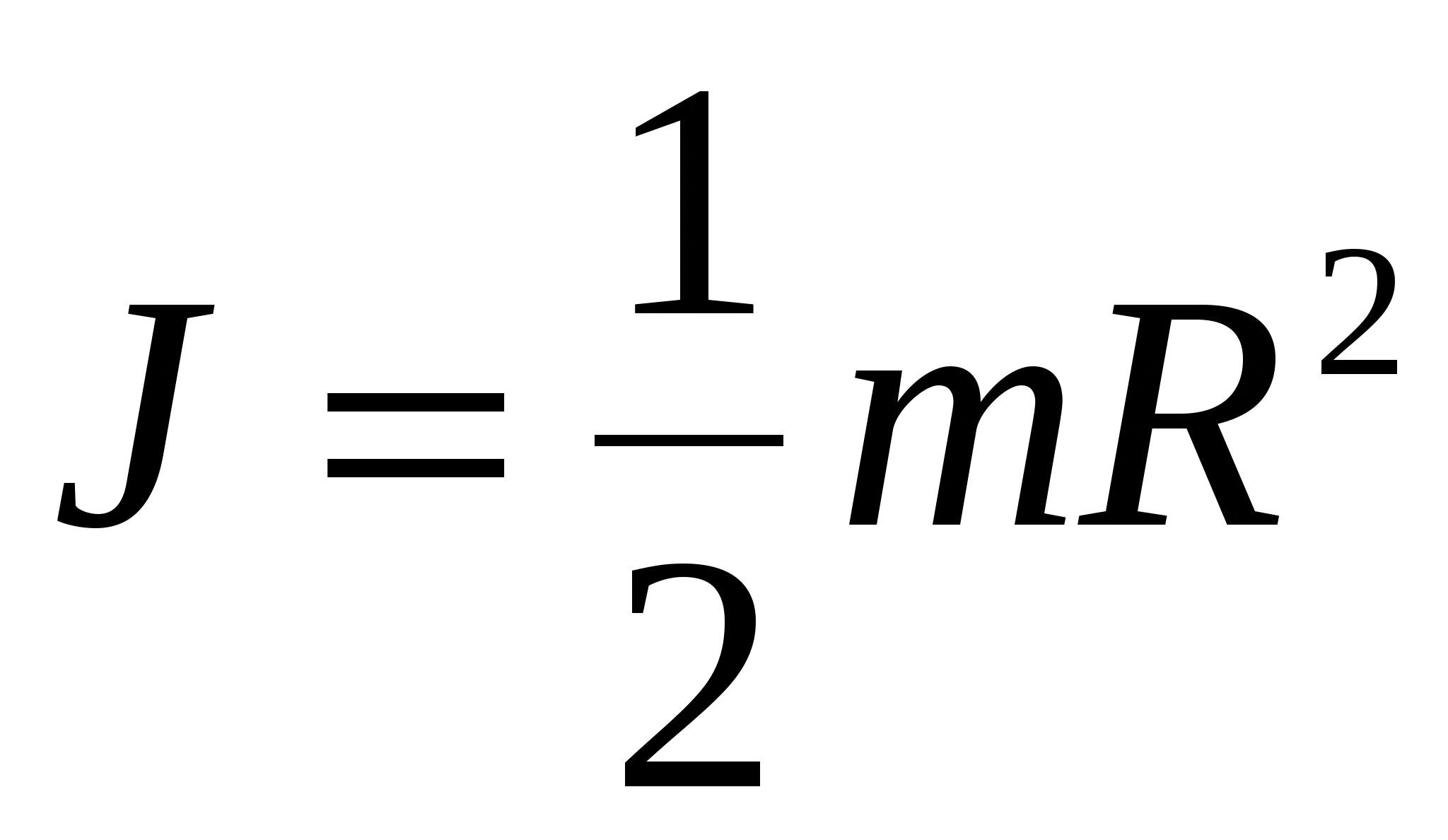 , ,
где R – радиус цилиндра и m – его масса.
Момент инерции полого цилиндра (обруча) с внутренним радиусом R1 и внешним R2 относительно оси цилиндра
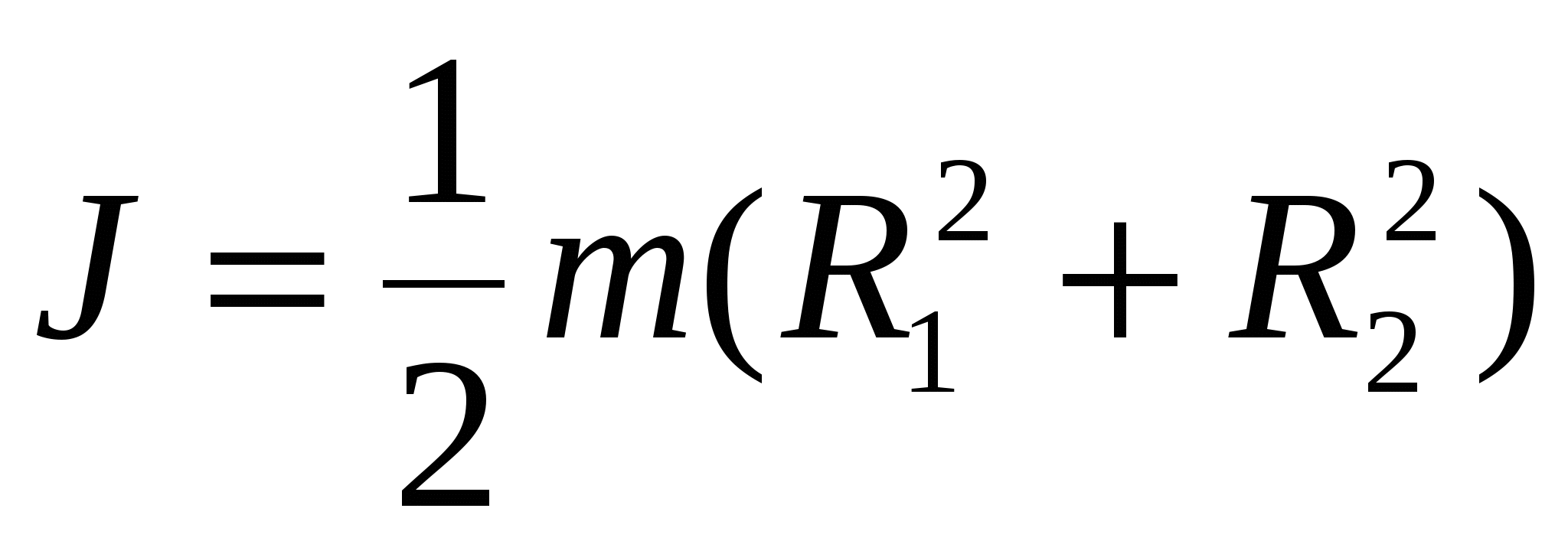 , ,
для тонкостенного полого цилиндра R1≈ R2=R и J≈mR2.
Момент инерции однородного шара радиусом R относительно оси, проходящей через его центр,
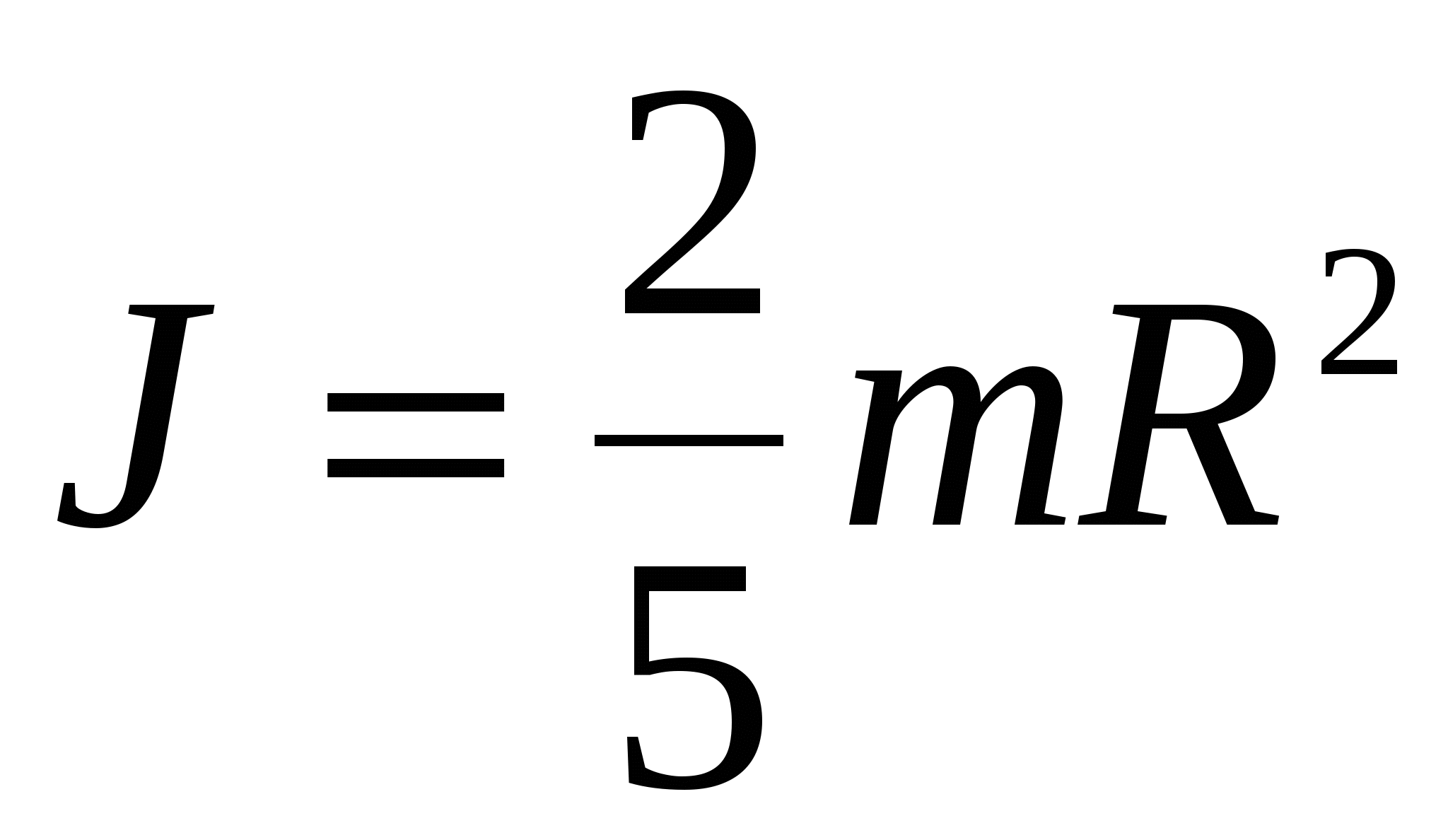 . .
Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно к нему,
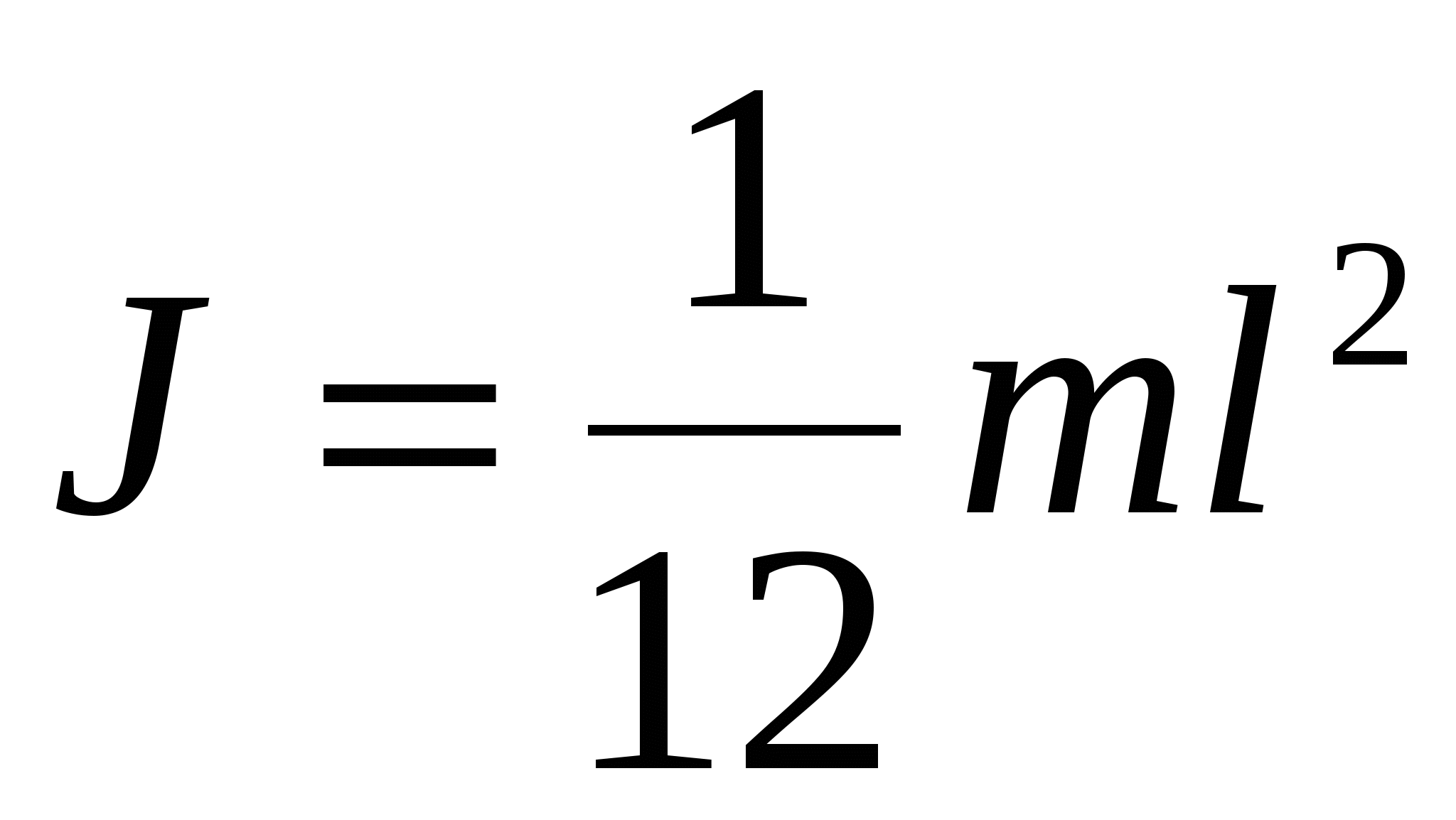 . .
Если для какого-либо тела известен его момент инерции J0 относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельно первой, может быть найден по формуле Штейнера
J=J0+md2,
где m – масса тела и D – расстояние от центра масс тела до оси вращения.
Основной закон динамики вращательного движения (закон сохранения момента импульса) выражается уравнением
M·dt=dL=d(Jω),
где M – момент сил, приложенных к телу, L – момент импульса тела (J – момент инерции тела, ω – его угловая скорость). Если J=const, то
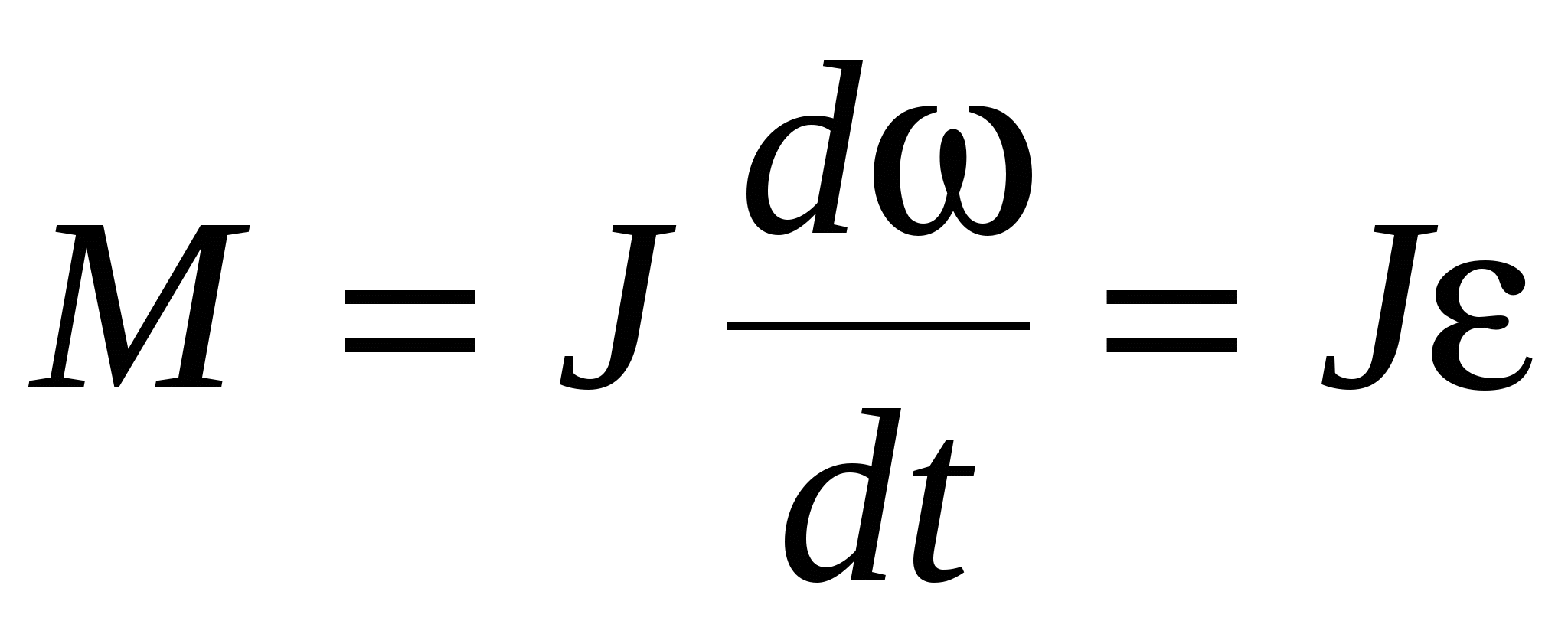 , ,
где ε – угловое ускорение, приобретаемое телом под действием момента сил M.
Кинетическая энергия вращающегося тела
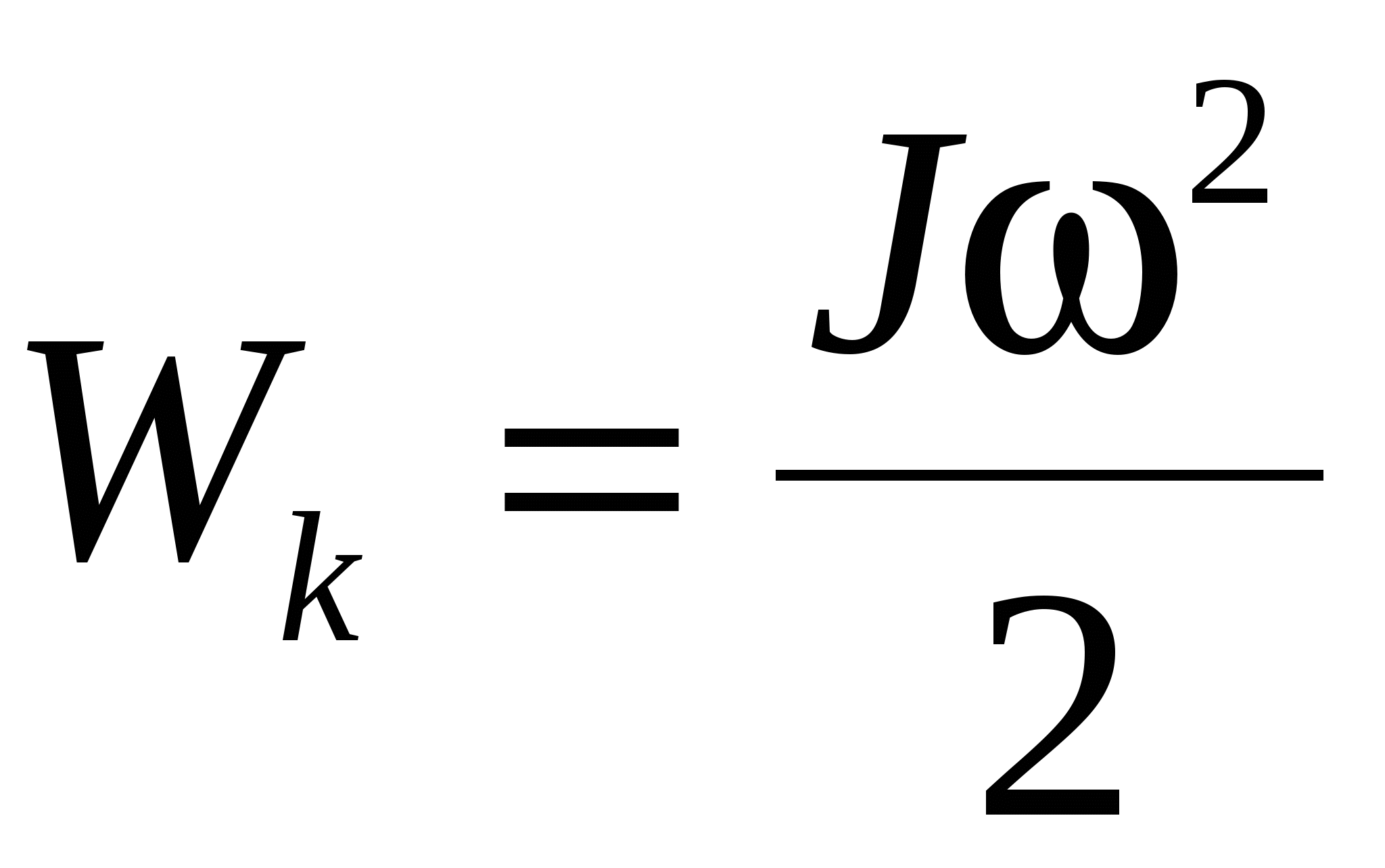 , ,
где J –момент инерции тела и ω – его угловая скорость.
Вывести формулу для момента инерции тонкого кольца радиусом R и массой m относительно оси симметрии. Ответ: J = mR2.
Определить момент инерции сплошного однородного диска радиусом R = 40 см и массой m= 1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Ответ: 0,12 кг·м2.
Определить момент инерции J тонкого однородного стержня длиной l = 50 см и массой m = 360 г относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от конца стержня на 1/6 его длины. Ответ: 1) 3·10-2 кг·м2; 2) 1,75·10-2 кг·м2.
Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра. Ответ: В 1,07 раза.
Полная кинетическая энергия Т диска, катящегося по горизонтальной поверхности, равна 24 Дж. Определить кинетическую энергию Т1 поступательного и Т2 вращательного движения диска. Ответ: Т1 = 16 Дж, Т2 = 8 Дж.
Полый тонкостенный цилиндр массой m = 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену υ1=1,4 м/с, после удара υ'1=1 м/с. Определить выделявшееся при ударе количество теплоты Q. Ответ: Q=m(υ12- υ'12) = 0,48 Дж.
Однородный стержень длиной l = 1 м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением ε вращается стержень, если на него действует момент сил М=98,1 мН·м? Ответ: 2,35 рад/с2.
К ободу однородного сплошного диска массой m = 10 кг, насажанного на ось, приложена постоянная касательная сила F = 30 H. Определить кинетическую энергию диска через время t = 4 с после начала действия силы. Ответ: 1,44 кДж.
Маховое колесо, момент инерции которого J = 245 кг·м2, вращается с частотой n=20 об/с. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. Ответ: 513 Н·м; 600.
Шар радиусом R= 10 см и массой m= 5 кг вращается вокруг оси симметрии согласно уравнению φ = А + Вt2 + Сt3 (В = 2 рад/с2, С = –0,5 рад/с3). Определить момент сил М для t= 3 с. Ответ: –0,1 Н·м.
Вентилятор вращается с частотой n = 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав N= 50 оборотов, остановился. Работа А сил торможения равна 31,4 Дж. Определить: момент М сил торможения; 2) момент инерции J вентилятора. Ответ: 1) 0,1 Н·м; 2) 15,9 мН·м.
Маховик в виде сплошного диска, момент инерции которого J=150 кг·м2, вращается с частотой n = 240 об/мин. Через время t=1 мин, как на маховик стал действовать момент сил торможения, он остановился. Определить: 1) момент М сил торможения; 2) число оборотов маховика от начала торможения до полной остановки. Ответ: 1) 62,8 Н·м; 2) 120.
Сплошной однородный диск скатывается без скольжения по наклонной плоскости, образующей угол α с горизонтом. Определить линейное ускорение а центра диска. Ответ: a = 2/3gsinα.
К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F = 400 H. При вращении диска на него действует момент сил трения Мтр= 2 Н·м. Определить массу m диска, если известно, что его угловое ускорение ε постоянно и равно 16 рад/с2. Ответ: 24 кг.
Частота вращения no маховика, момент инерции J которого равен 120 кг·м2, составляет 240 об/мин. После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время t = π мин. Считая трение в подшипниках постоянным, определить момент М сил трения. Ответ: 16 Н·м.
Маховик в виде сплошного диска, момент инерции которого J=1,5 кг·м2, вращаясь при торможении равнозамедленно, за время t= 1 мин уменьшил частоту своего вращения с n0 = 240 об/мин до n1 = 120 об/мин. Определить: 1) угловое ускорение ε маховика; 2) момент М силы торможения; 3) работу торможения А. Ответ: 1) 0,21 рад/с2, 2) 0,047 Н·м; 3) 355 Дж.
Колесо радиусом R = 30 см и массой m = 3 кг скатывается по наклонной плоскости длиной 1 = 5 м и углом наклона α = 25°. Определить момент инерции колеса, если его скорость υ в конце движения составляла 4,6 м/с. Ответ: 0,259 кг·м2.
С наклонной плоскости, составляющей угол α = 30° к горизонту, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см. Ответ: 0,585 с.
На однородный сплошной цилиндрический вал радиусом R = 50 cм намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз, разматывая нить, опускается с ускорением а = 2 м/с2. Определить: 1) момент инерции J вала; 2) массу М вала. Ответ: 1) 6,25 кг·м2; 2) 50 кг.
На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции которого J = 0,15 кг·м2, намотана легкая нить, к концу которой прикреплен груз массой m = 0,5кг. До начала вращения барабана высота h груза над полом составляла 2,3 м. Определить: 1) время опускания груза до пола; 2) силу натяжения нити; 3) кинетическую энергию груза в момент удара о пол. Ответ: 1) 2 с; 2) 4,31 Н; 3) 1,32 Дж.
Через неподвижный блок в виде однородного сплошного цилиндра массой m = 0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами m1= 0,35 кг и m2 = 0,55 кг. Пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) отношение T2/T1 сил натяжения нити. Ответ: 1) 1,96 м/с2; 2) 1,05.
Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, Wк = 60 Дж. Найти момент импульса L вала. Ответ: 3,8 кг·м2/с.
Карандаш длиной l=15 см, поставленный вертикально, падает на стол. Какую угловую скорость ω и линейную скорость υ будут иметь в конце падения середина и верхний конец карандаша? Ответ: ωс= ωк=14 рад/с; υс=1,05 м/с, υк=2,1 м/с.
Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением ε = 0,4 рад/с2. Определить кинетическую энергию маховика через время t2 = 25 с после начала движения, если через t1 = 10 с после начала движения момент импульса L1 маховика составлял 60кг·м2/с. Ответ: 1) Ек = 75 Дж.
Горизонтальная платформа массой m = 25 кг и радиусом R= 0,8 м вращается с частотой n1 = 18 мин-1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от J1 = 3,5 кг·м2 до J2 = 1 кг·м2. Ответ: 23 мин-1.
Человек, стоящий на скамье Жуковского, держит в руках стержень длиной l= 2,5 м и массой m = 8 кг, расположенный вертикально вдоль оси вращения скамейки. Эта система (скамья и человек) обладает моментом инерции J = 10 кг·м2 и вращается с частотой n1 = 12 мин-1. Определить частоту n2 вращения системы, если стержень повернуть в горизонтальное положение. Ответ: 8,5 мин-1.
Человек массой T = 60 кг, стоящий на краю горизонтальной платформы массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1=10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить, с какой частотой будет тогда вращаться платформа. Ответ: 20 мин-1.
Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определять, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы. Ответ: Возрастет в 1,43 раза.
Человек массой m = 60 кг, стоящий на краю горизонтальной платформы радиусом R = 1 м массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1 = 10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру. Ответ: 65,8 Дж.
Однородный стержень длиной l = 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через его верхний конец. Найти период колебаний Т стержня. Ответ: 1,16 с.
Обруч диаметром D = 56,5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период колебаний Т обруча. Ответ: 1,5 с.
Элементы специальной теории относительности
Длина l тела, движущегося со скоростью υ относительно некоторой системы отсчета, связана с длиной l0 тела, неподвижного в этой системе, соотношением
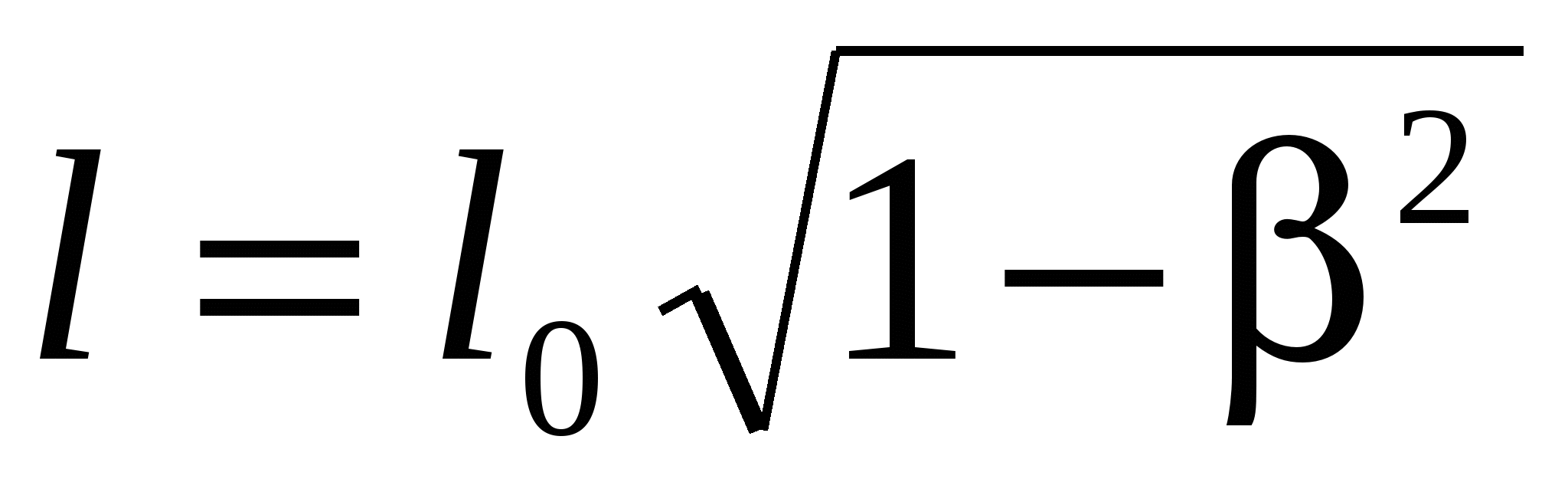 , ,
где β=υ/с, с – скорость распространения света.
Промежуток времени Δτ в системе, движущейся со скоростью υ по отношению к наблюдателю, связан с промежутком времени Δτ0 в неподвижной для наблюдателя системе соотношением
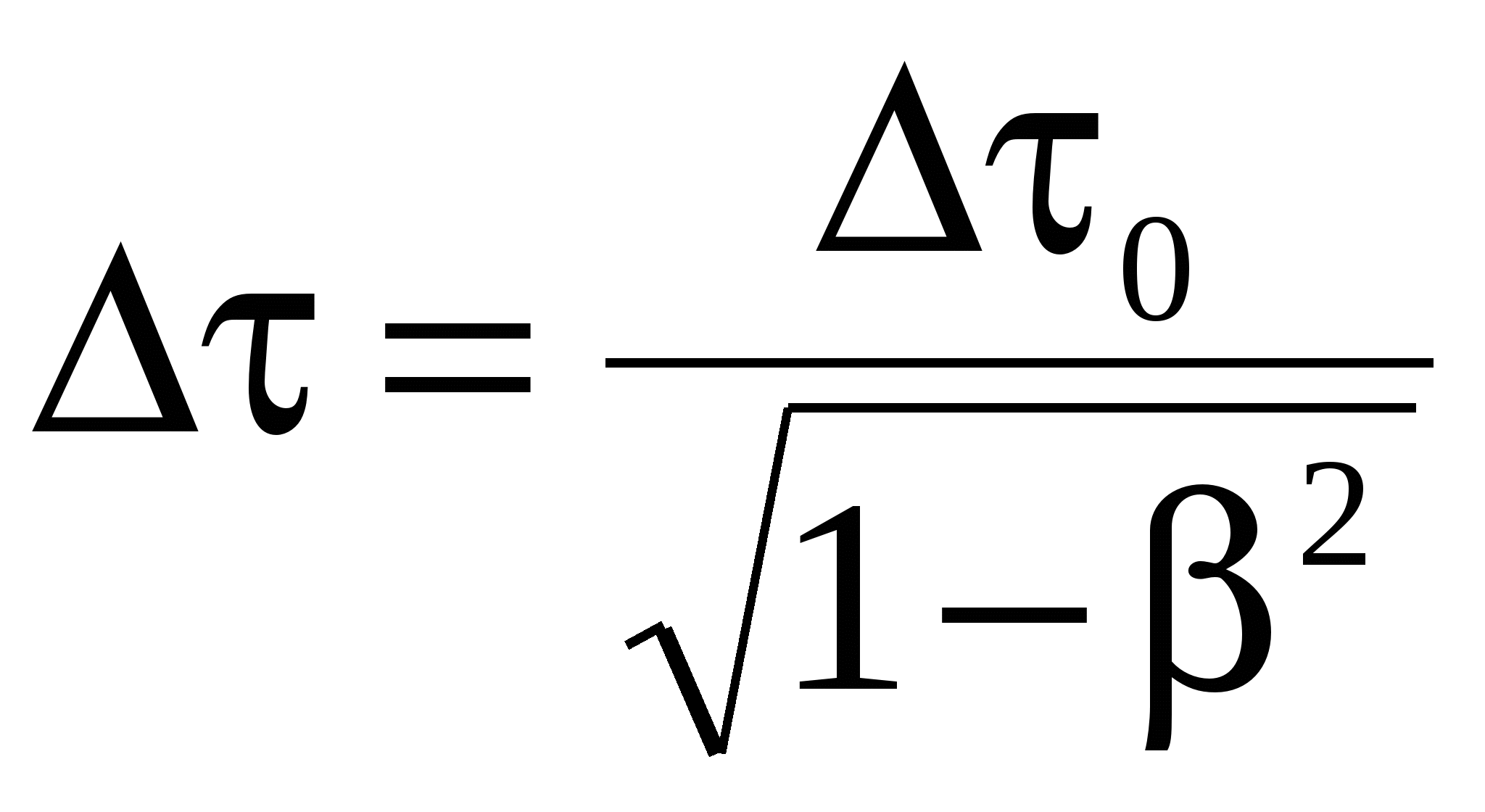 . .
Зависимость массы m тела от скорости υ его движения дается уравнением
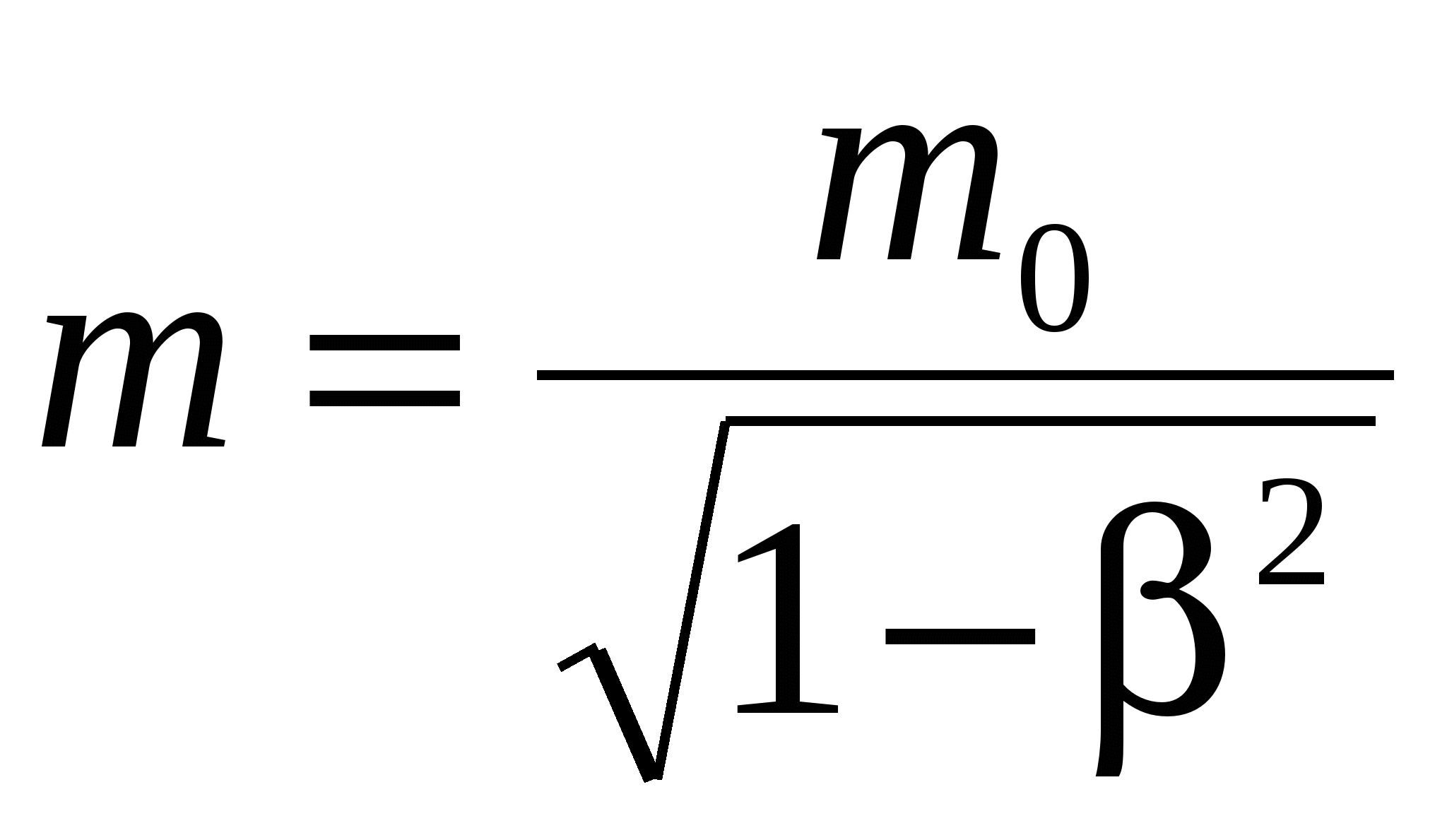 , ,
где m0 – масса покоя этого тела.
Зависимость кинетической энергии тела от скорости υ его движения дается уравнением
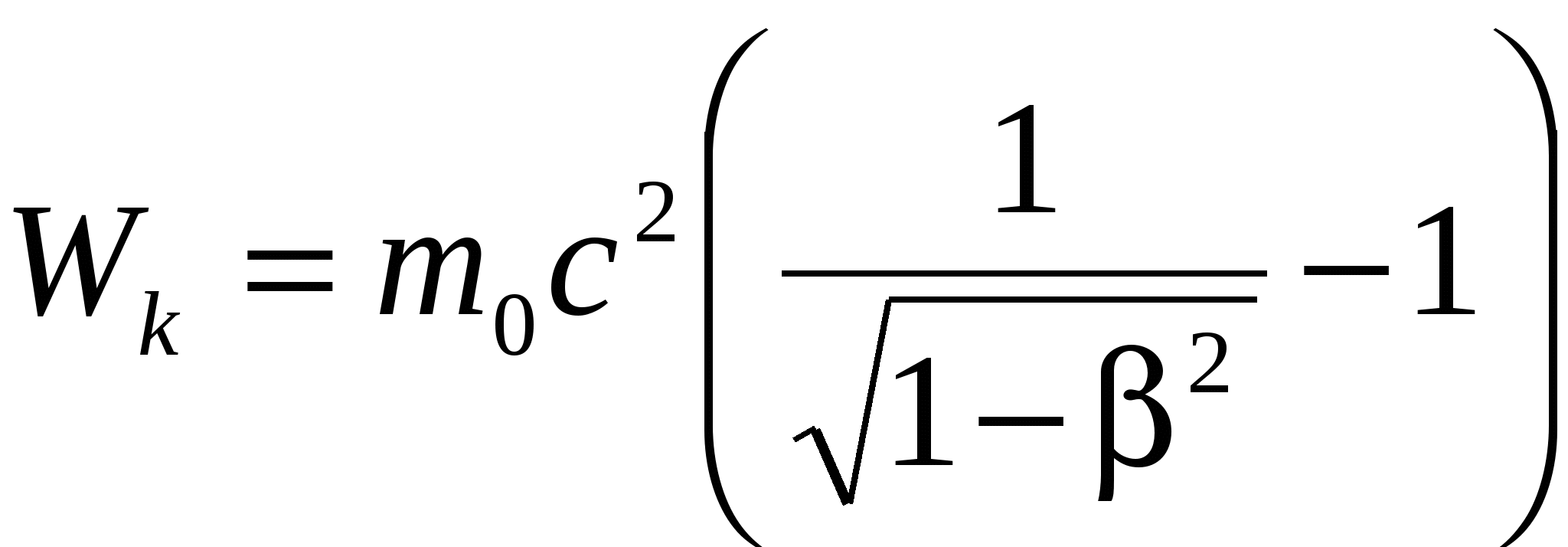 . .
Изменение массы системы на Δm соответствует изменению энергии системы на
ΔW=c2 Δm.
Релятивистский закон сложения скоростей для тела, движущегося вдоль оси OX, имеет вид
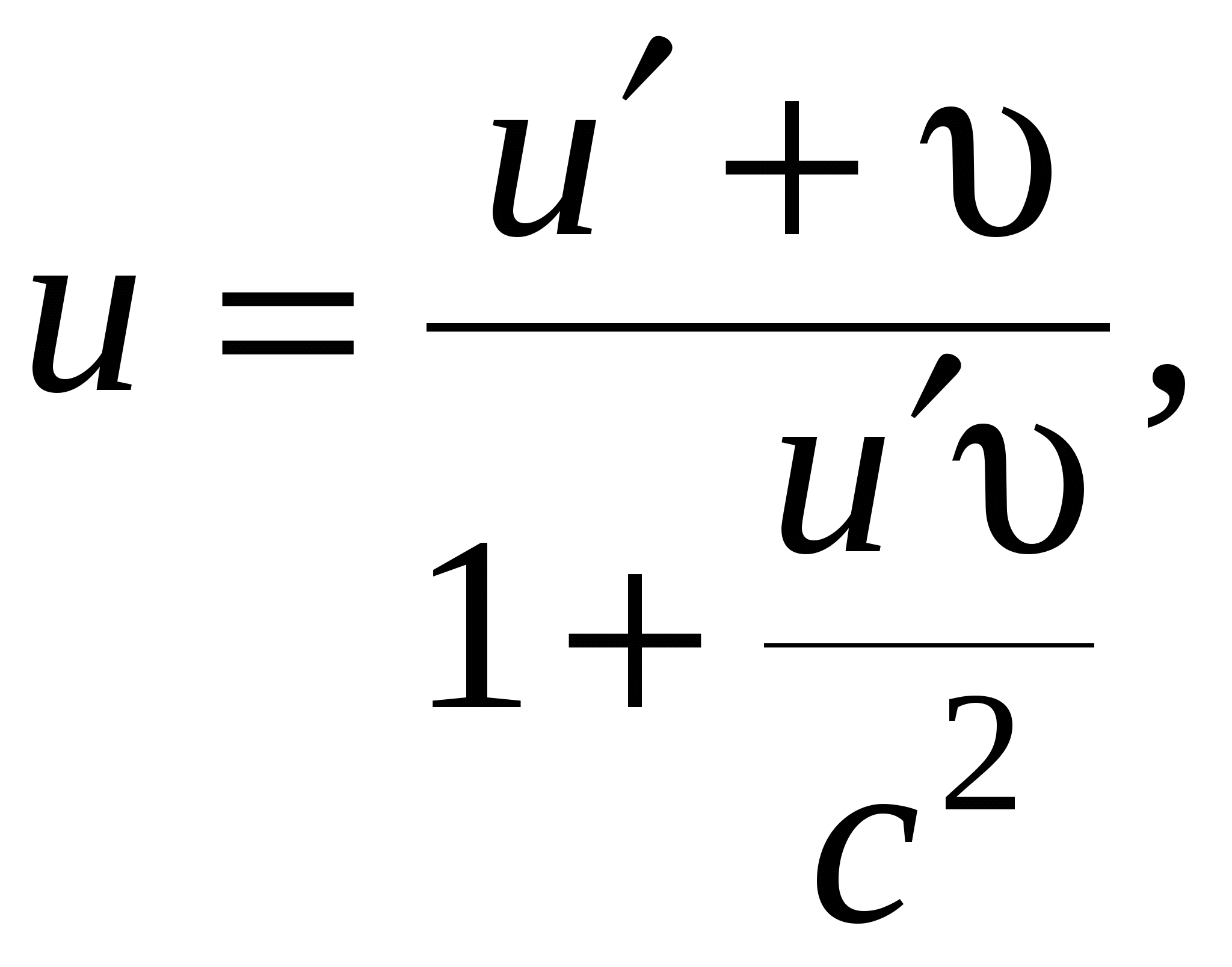
где υ – скорость движущейся системы отсчета K′, u′ – скорость относительно системы K′, u– скорость относительно неподвижной.
Две нестабильные частицы движутся в системе отсчета К в одном направлении вдоль одной прямой с одинаковой скоростью υ = 0,6 с. Расстояние между частицами в системе К равно 64 м. Обе частицы распались одновременно в системе К', которая связана с ними. Определить промежуток времени между распадом частиц в системе К. Ответ: 0,2 мкс.
Определить, во сколько раз увеличивается время жизни нестабильной частицы (по часам неподвижного наблюдателя), если она начинает двигаться со скоростью, равной 0,9 с. Ответ: В 2,29 раза.
Собственное время жизни частицы отличается на 1 % от времени жизни по неподвижным часам. Определить β = υ/c. Ответ: 0,141.
Космический корабль движется со скоростью υ = 0,8 с по направлению к Земле. Определить расстояние, пройденное им в системе отсчета, связанной с Землей (системе К), за to = 0,5 с, отсчитанное по часам в космическом корабле (системе К'). Ответ: 200 Мм.
Мюоны, рождаясь в верхних слоях атмосферы, при скорости υ = 0,995 с пролетают до распада l = 6 км. Определить: 1) собственную длину пути, пройденную ими до распада; 2) время жизни мюона для наблюдателя на Земле; 3) собственное время жизни мюона. Ответ: 1) 599 м; 2) 20,1 мкс; 3) 2 мкс.
Определить относительную скорость движения, при которой релятивистское сокращение линейных размеров тела составляет 10%. Ответ: 1,31·105 км/с.
В системе К' покоится стержень (собственная длина l0 = 1,5 м), ориентированный под углом θ' = 30° к оси Ох'. Система К' движется относительно системы К со скоростью υ = 0,6 с. Определить в системе К: 1) длину стержня 1; 2) соответствующий угол 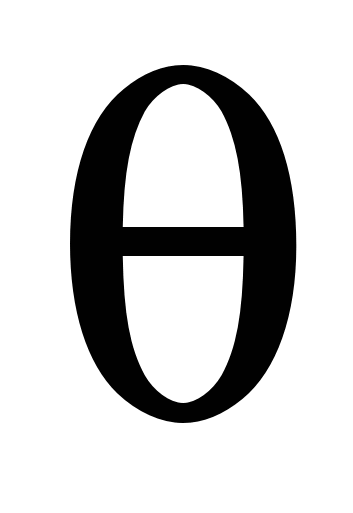 . Ответ: 1) 1,28 м; 2) 35°48'. . Ответ: 1) 1,28 м; 2) 35°48'.
Определить собственную длину стержня, если в лабораторной системе его скорость υ = 0,6 с, длина l = 1,5 м и угол между ним и направлением движения 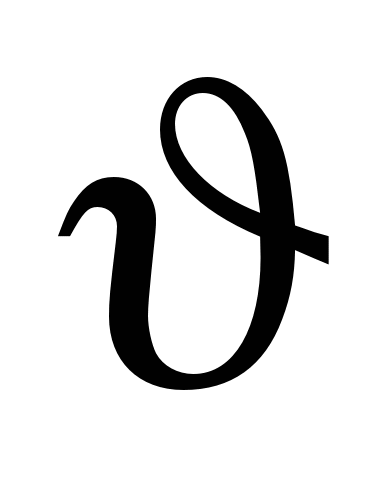 =30°. Ответ: 1,79 м. =30°. Ответ: 1,79 м.
Ионизованный атом, вылетев из ускорителя со скоростью 0,8 с, испустил фотон в направлении своего движения. Определить скорость фотона относительно ускорителя. Ответ: с.
Две ракеты движутся навстречу друг другу относительно неподвижного наблюдателя с одинаковой скоростью, равной 0,5 с. Определить скорость сближения ракет, исходя из закона сложения скоростей: 1) в классической механике; 2) в специальной теории относительности. Ответ: 1) с; 2) 0,8 с.
Частица движется со скоростью υ = 0,8 с. Определить отношение массы релятивистской частицы к ее массе покоя. Ответ: 1,67.
Определить на сколько процентов масса релятивистской элементарной частицы, вылетающей из ускорителя со скоростью υ = 0,75 с, больше ее массы покоя Ответ: На 51,2%.
Определить скорость движения релятивистской частицы, если ее масса в два раза больше массы покоя. Ответ: 0,866 с.
Определить релятивистский импульс протона, если скорость его движения υ = 0,8с. Ответ: 6,68·10-19 кг·м/с.
Определить скорость, при которой релятивистский импульс частицы превышает ее ньютоновский импульс в n = 3 раза. Ответ: 0,943 с.
Полная энергия релятивистской частицы в 8 раз превышает ее энергию покоя. Определить скорость этой частицы. Ответ: 298 Mм/c.
Кинетическая энергия частицы оказалась равной ее t энергии покоя. Определить скорость частицы. Ответ: 260 Мм/с.
Определить релятивистский импульс p и кинетическую энергию Т протона, движущегося со скоростью υ = 0,75 с. Ответ: 5,68·10-19 кг·м/с; 7,69·10-11 Дж.
Определить кинетическую энергию электрона, если масса движущегося электрона втрое больше его массы покоя. Ответ выразить в электронвольтах. Ответ: 1,02 МэВ.
Определить работу, которую необходимо совершить, чтобы увеличить скорость частицы с массой покоя mo от 0,5 с до 0,7 с. Ответ: 0,245 moс2.
Определить релятивистский импульс электрона, кинетическая энергия которого Т= 1 ГэВ. Ответ: 5,34·10-19 кг·м/с.
|
|
|
 Скачать 0.66 Mb.
Скачать 0.66 Mb.