5. Механические колебания и волны
Уравнение гармонического колебательного движения имеет вид
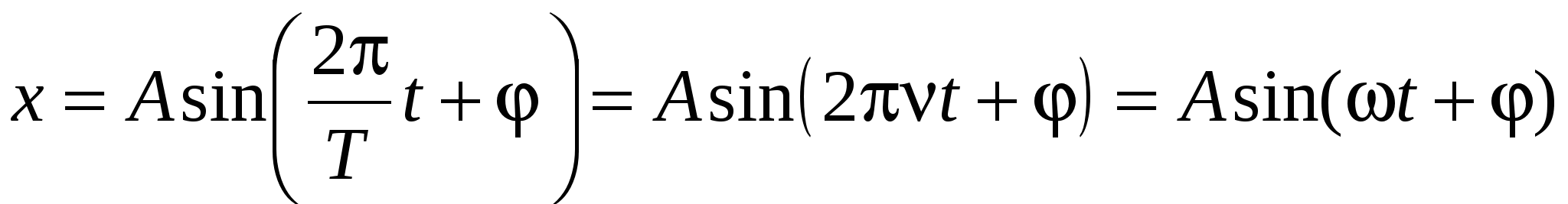 , ,
где x – смещение точки от положения равновесия, разное для разных моментов времени, А – амплитуда, Т – период, φ – начальная фаза, ν [Гц]=1/Т – частота колебаний, ω [с-1]=2π/Т – круговая частота.
Скорость и ускорение точки, совершающей колебание, определяются соотношениями
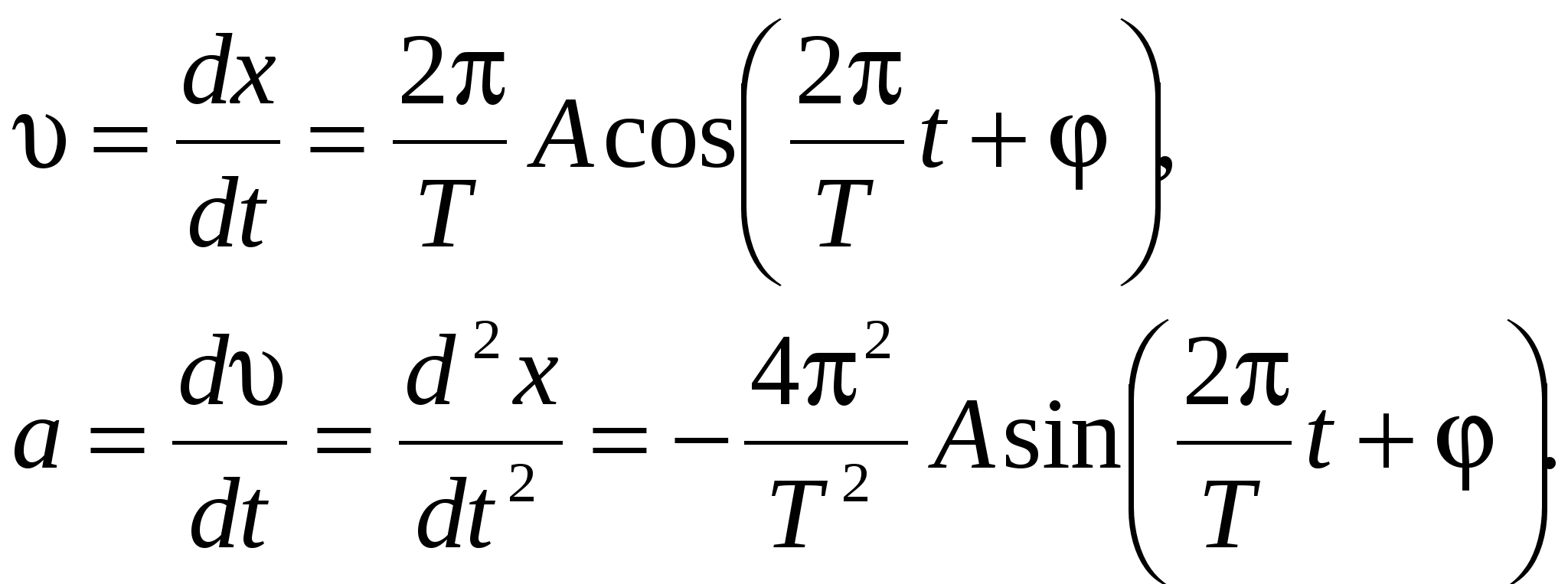
Сила, под действием которой точка массой m совершает гармоническое колебание,
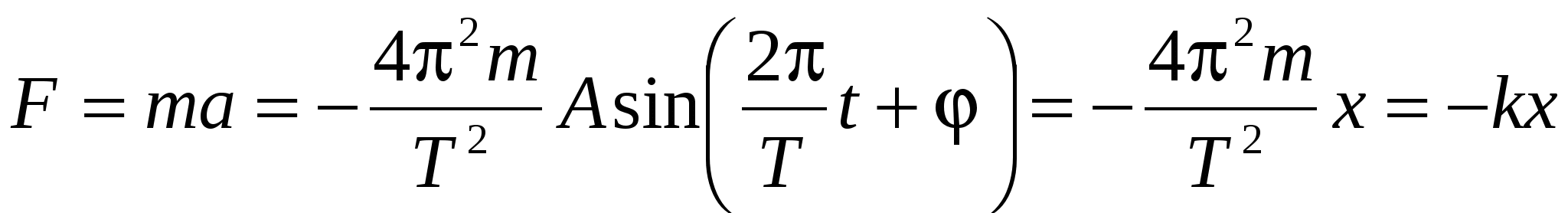 , ,
где k = 4π2m/T, T = 2π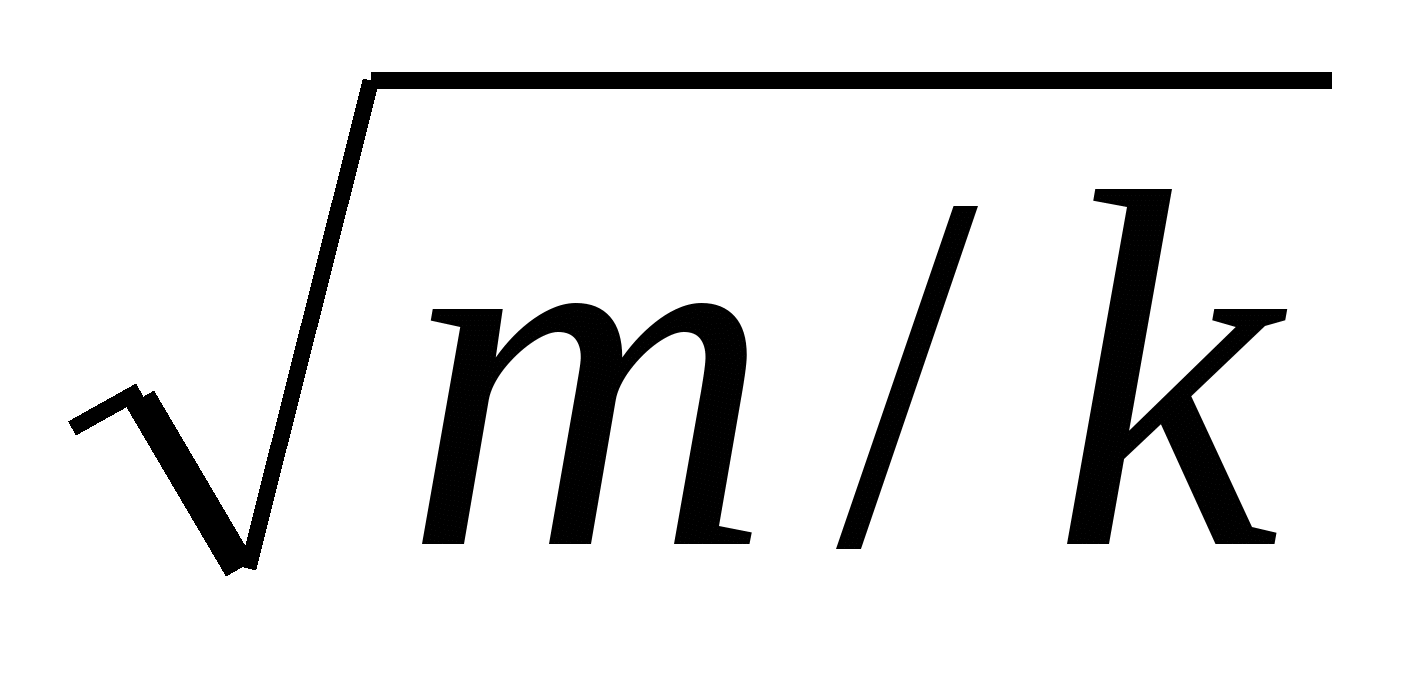 . Здесь Т – период колебаний точки, совершающей колебания под действием силы F = –kx, где k – жесткость, численно равная силе, вызывающей смещение, равное единице. . Здесь Т – период колебаний точки, совершающей колебания под действием силы F = –kx, где k – жесткость, численно равная силе, вызывающей смещение, равное единице.
Кинетическая и потенциальная энергии колеблющейся точки имеют вид
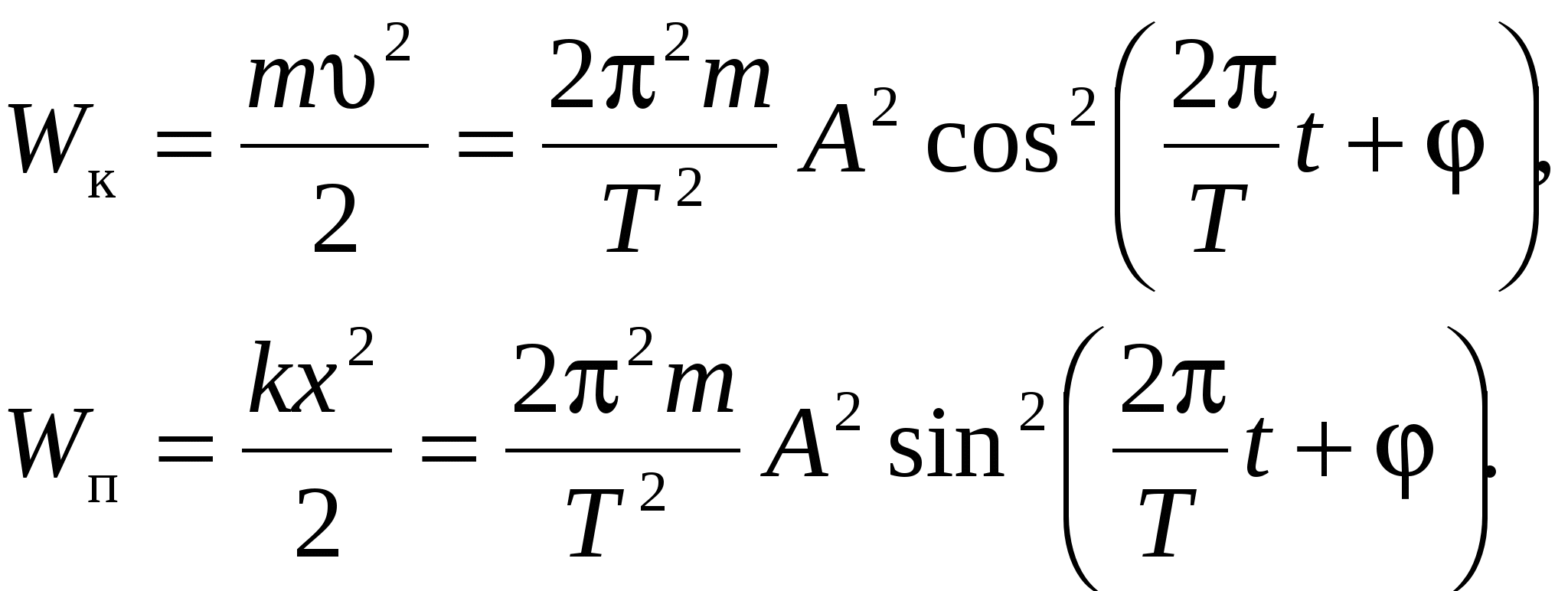
Полная энергия
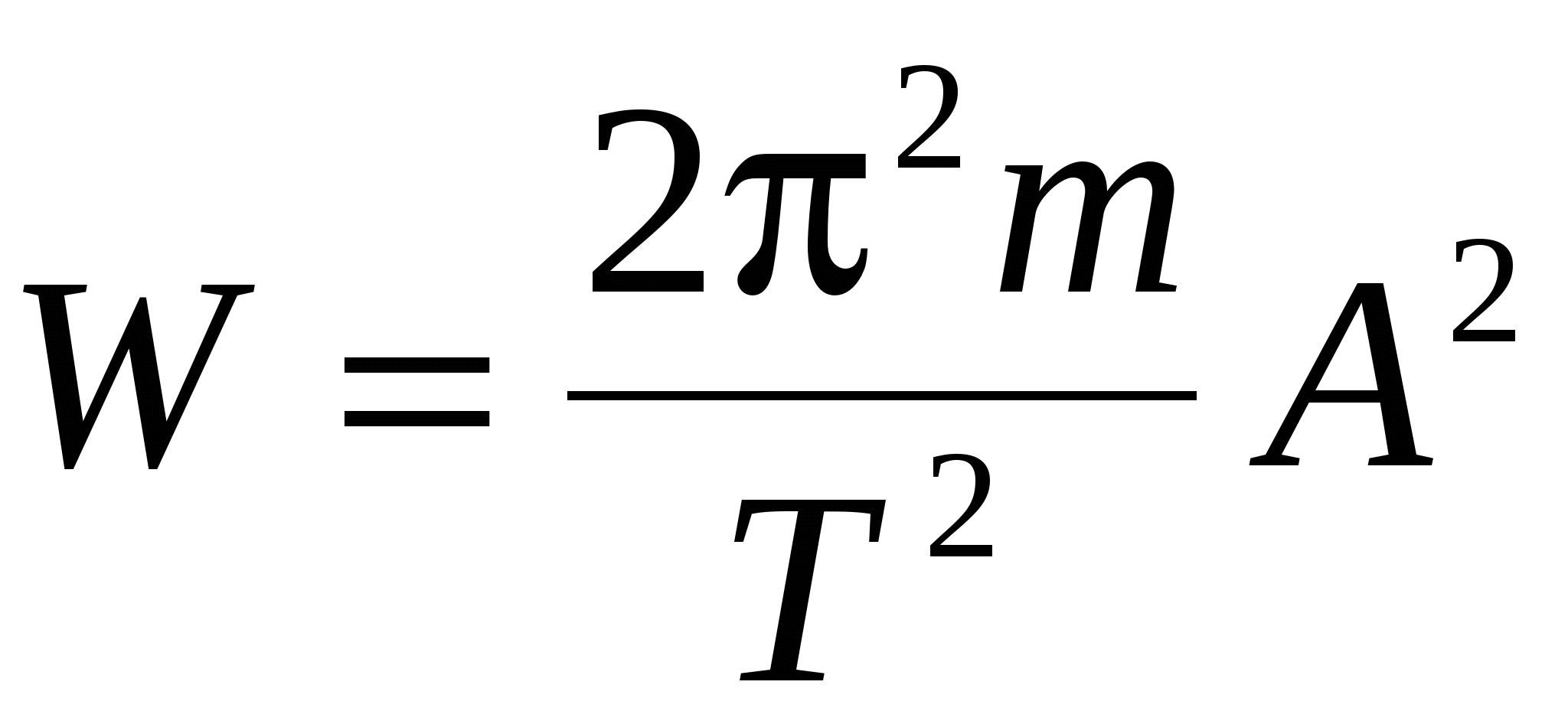 . .
Примером гармонических колебательных движений могут служить малые колебания маятника. Период колебаний математического маятника
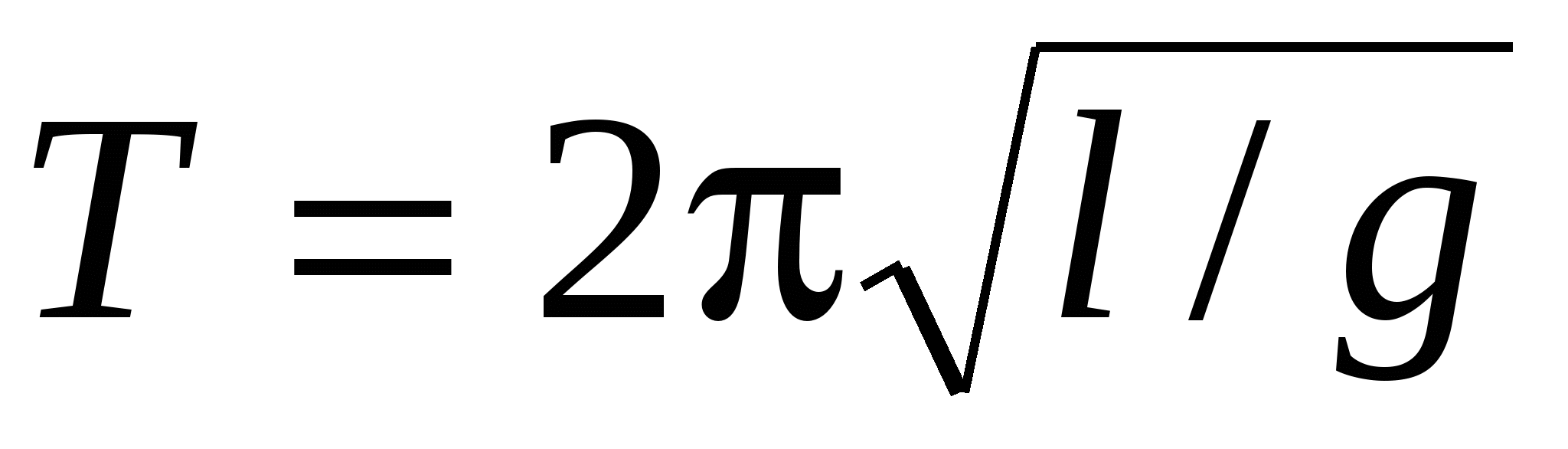 , ,
где l – длина маятника, g – ускорение свободного падения.
При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой
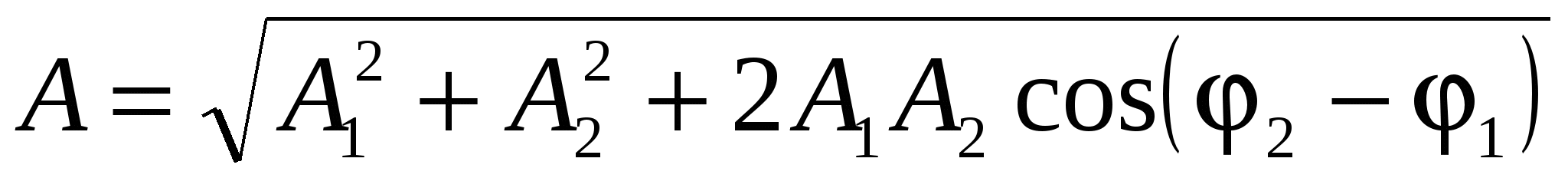
и с начальной фазой, определяемой из уравнения
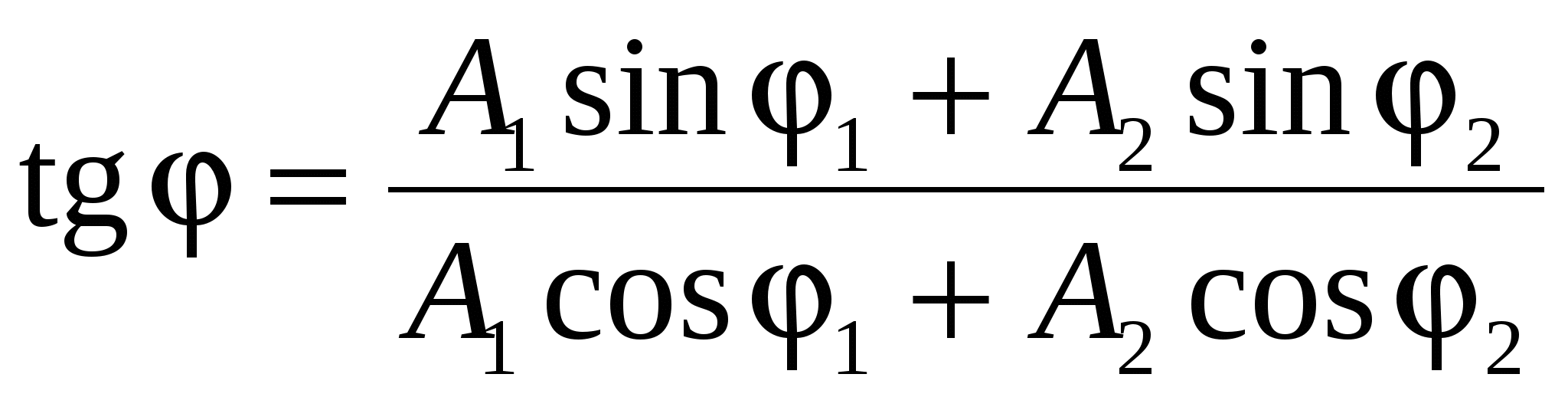 , ,
где А1 и А2 – амплитуды слагаемых колебаний, φ1 и φ2 – их начальные фазы.
При сложении двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории результирующего движения имеет вид
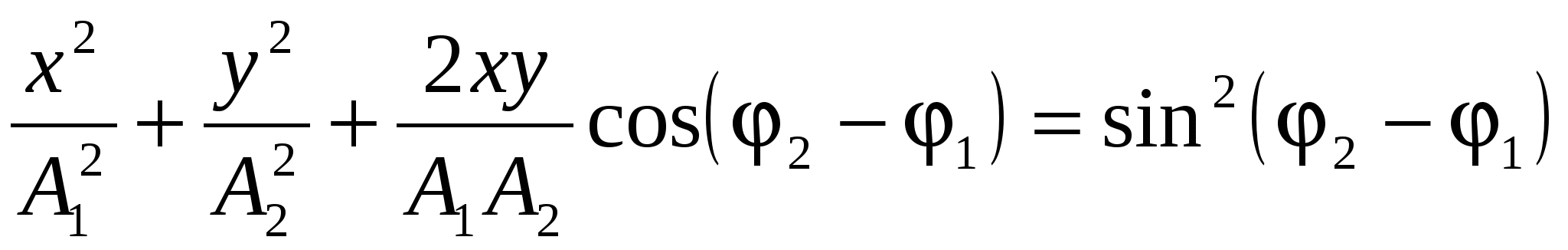 . .
Если на материальную точку массой m, кроме упругой силы F = –kx, действует еще сила трения Fтр = –rυ, где r – коэффициент трения и υ – скорость колеблющейся точки, то колебания точки будут затухающими. Уравнение затухающего колебательного движения имеет вид x = Ae-δtsin(ωt+φ), где δ [с-1] – коэффициент затухания. При этом δ = r/2m и 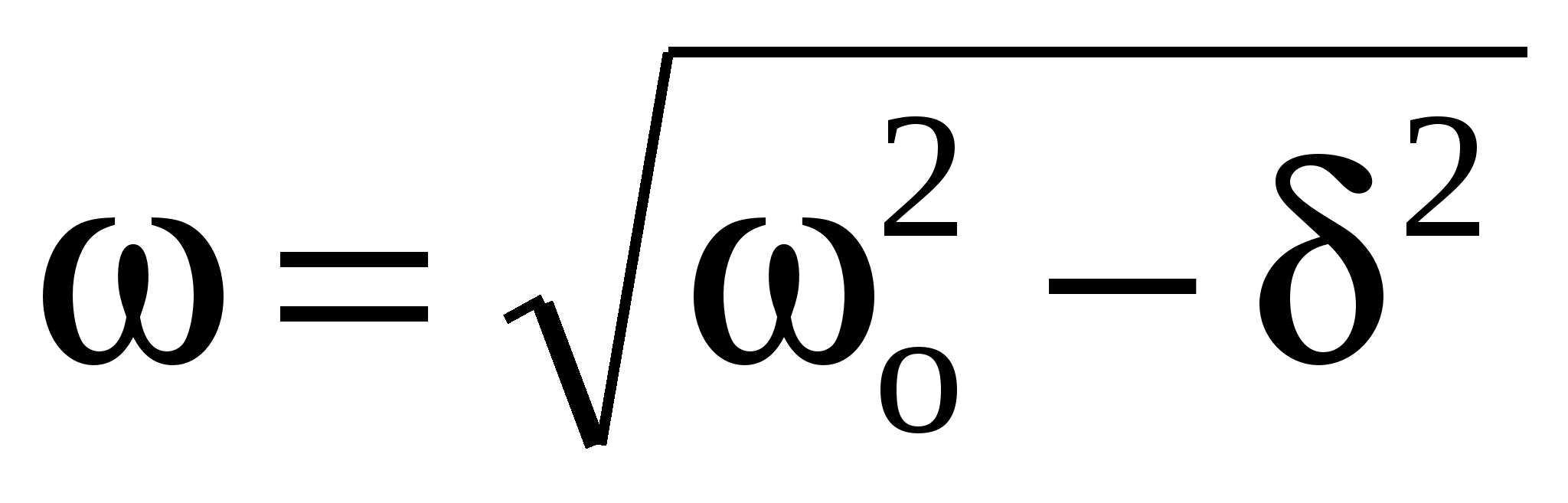 , где ωо – круговая частота собственных колебаний. Величина æ = δТ, называется логарифмическим декрементом затухания. , где ωо – круговая частота собственных колебаний. Величина æ = δТ, называется логарифмическим декрементом затухания.
Если на материальную точку массой m, колебание которой дано в виде x1 = Ae-δtsinωоt, действует внешняя периодическая сила F = Fosinωt, то колебания точки будут вынужденными и уравнение ее движения примет вид x2 = Asin(ωt+φ),
где 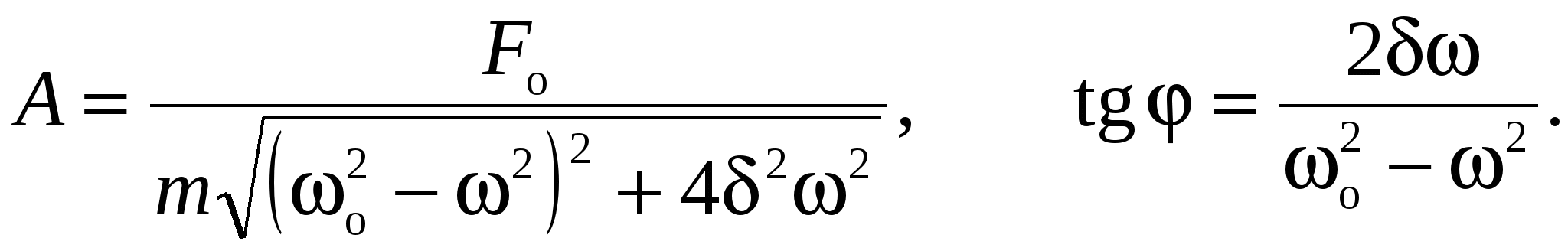
Резонанс наступает тогда, когда частота вынужденных колебаний ω связана с частотой собственных колебаний ωо и с коэффициентом затухания δ соотношением 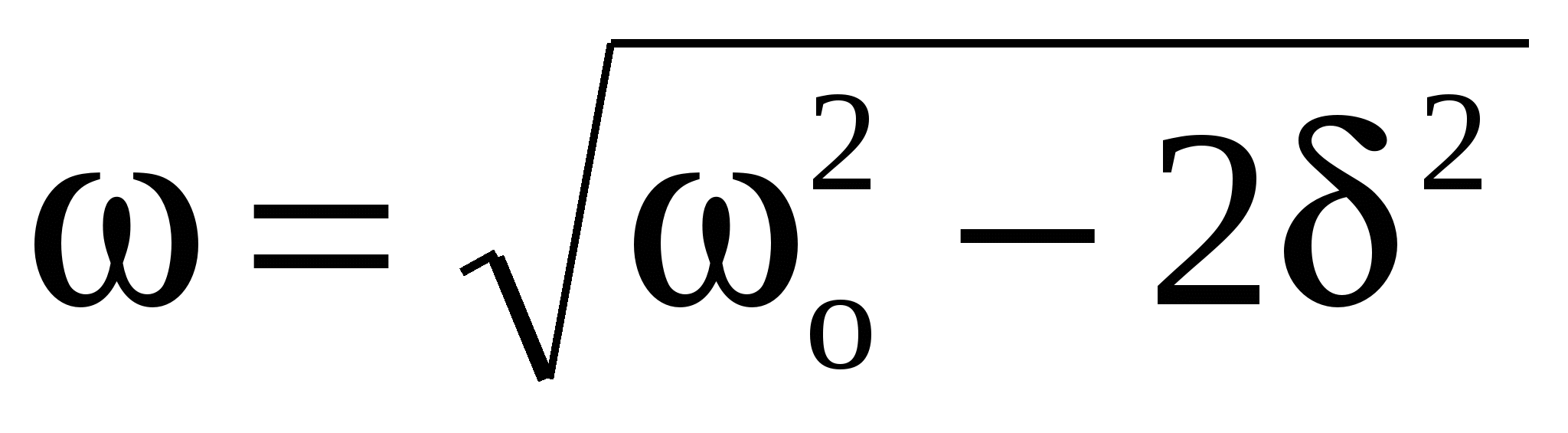 . .
При распространении незатухающих колебаний со скоростью с вдоль некоторого направления, называемого лучом, смещение любой точки, лежащей на луче и отстоящей от источника колебаний на расстоянии l, дается уравнением
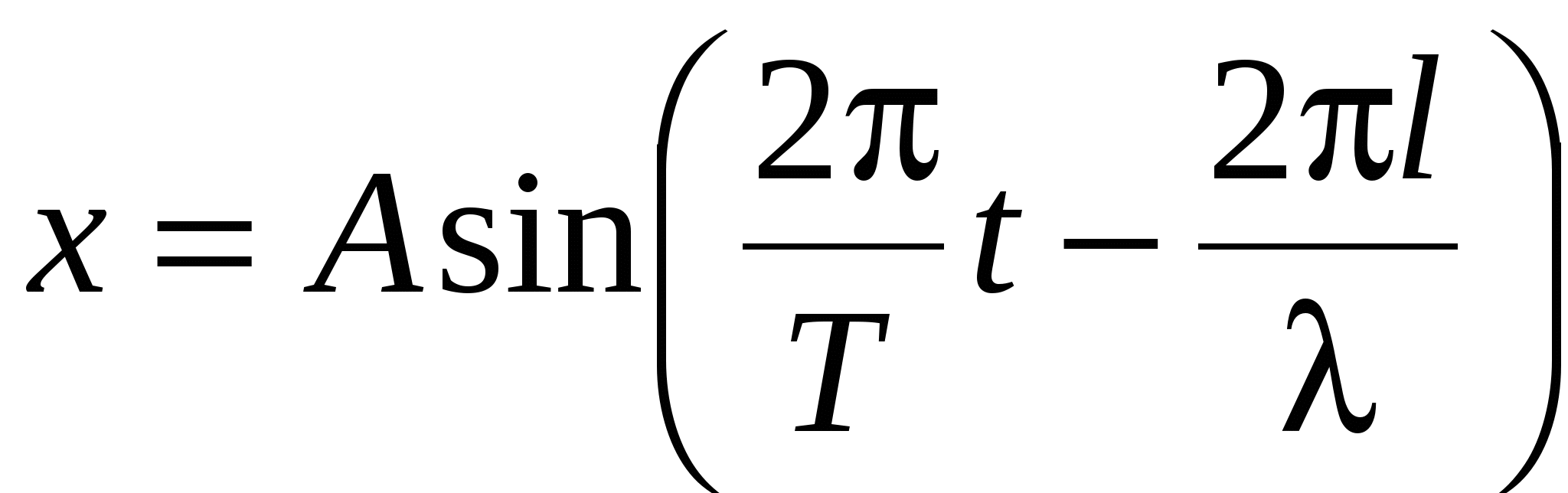 , ,
где А – амплитуда колеблющихся точек, λ –длина волны. При этом λ=сТ. Две точки, лежащие на луче на расстояниях l1 и l2 от источника колебаний, имеют разность фаз
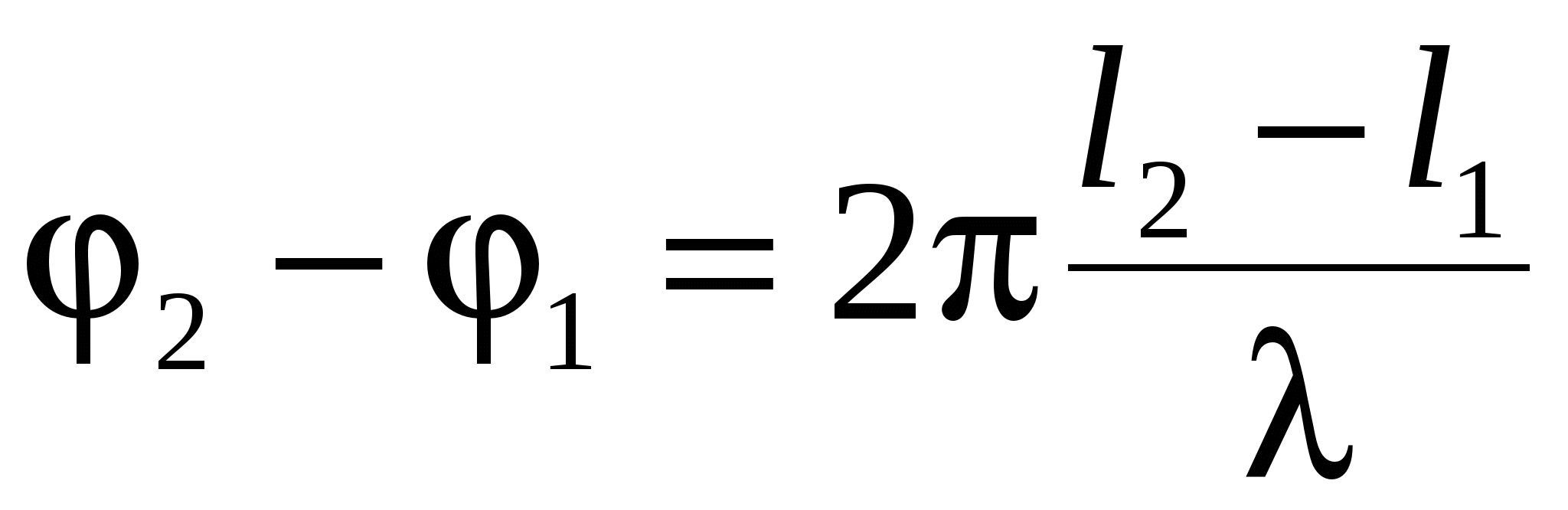 . .
При интерференции волн максимум и минимум амплитуды получаются соответственно при условиях
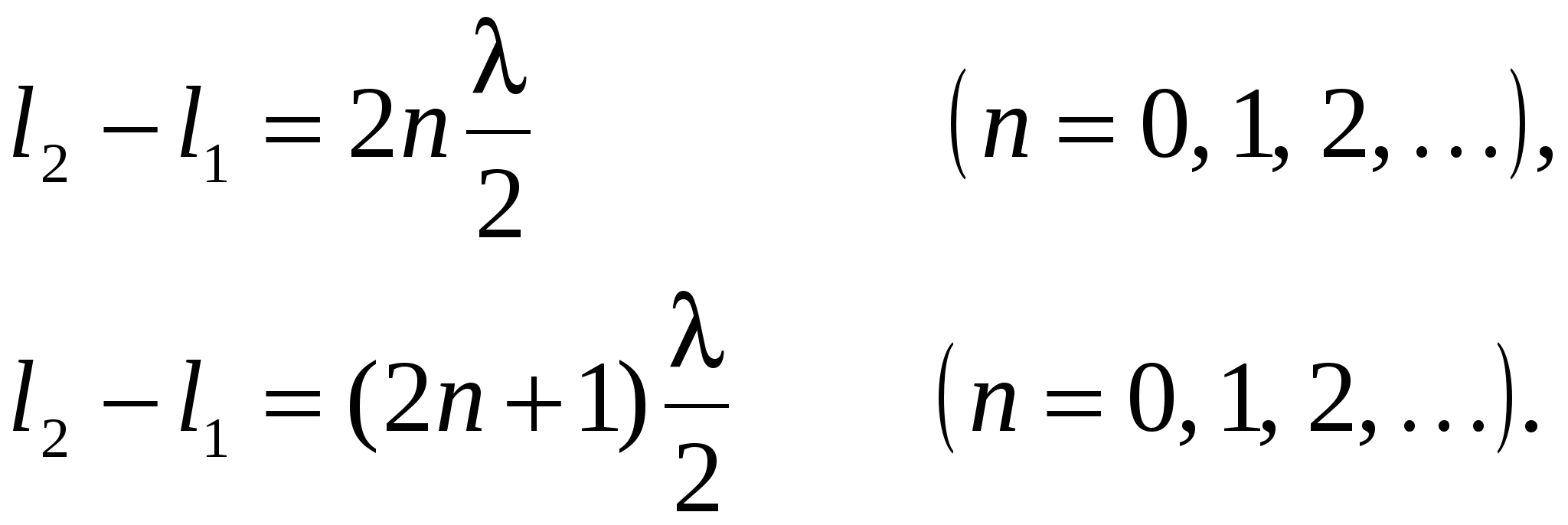
Здесь l2 – l1 – разность хода лучей.
Точка совершает гармонические колебания с периодом Т= 6 с и начальной фазой, равной нулю. Определить, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды. Ответ: 1 с.
Точка совершает гармонические колебания по закону 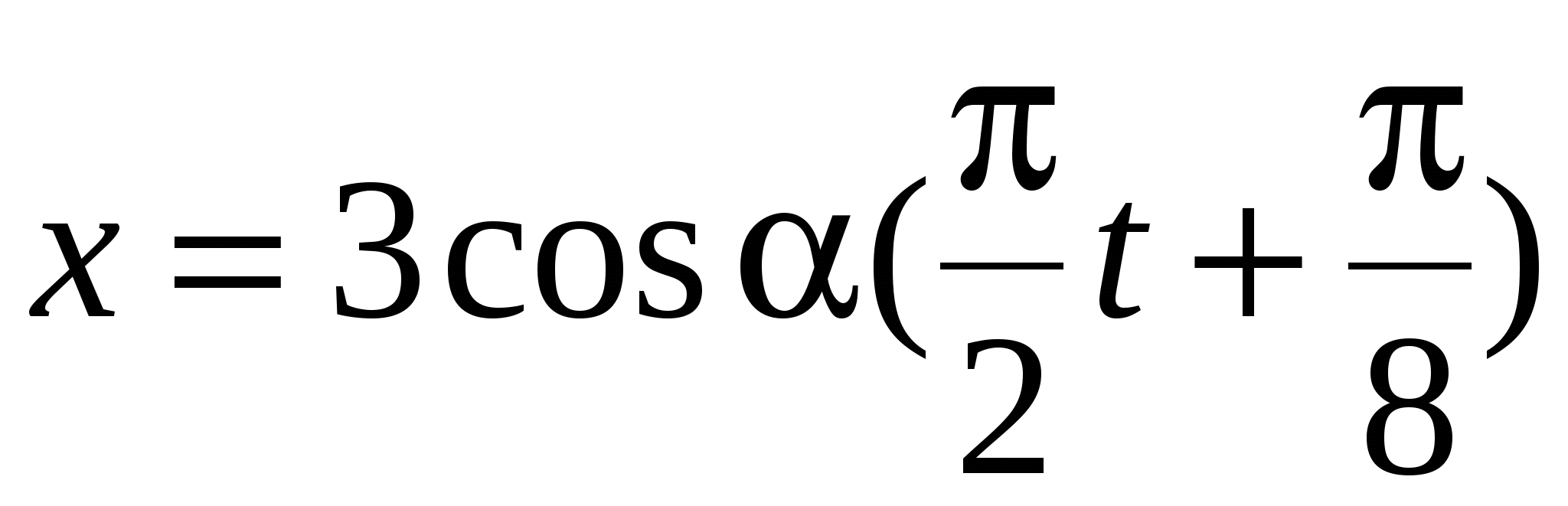 м. Определить: 1) период Т колебаний; 2) максимальную скорость υmax точки; 3) максимальное ускорение аmax точки. Ответ:1) Т = 4 с; 2) υmax = 4,71 м/с, 3) аmax =7,4 м/с2. м. Определить: 1) период Т колебаний; 2) максимальную скорость υmax точки; 3) максимальное ускорение аmax точки. Ответ:1) Т = 4 с; 2) υmax = 4,71 м/с, 3) аmax =7,4 м/с2.
Точка совершает гармонические колебания с амплитудой А =10 см и периодом Т=5 с. Определить для точки: 1) максимальную скорость; 2) максимальное ускорение. Ответ:1) 12,6 см/с; 2) 15,8 см/с2.
Материальная точка совершает колебания согласно уравнению x = Asinωt. В какой-то момент времени смещение точки x1 = 15см. При возрастании фазы колебаний в два раза смещение x2 оказалось равным 24 см. Определить амплитуду А колебаний. Ответ: 25 см.
Материальная точка совершает гармонические колебания согласно уравнению 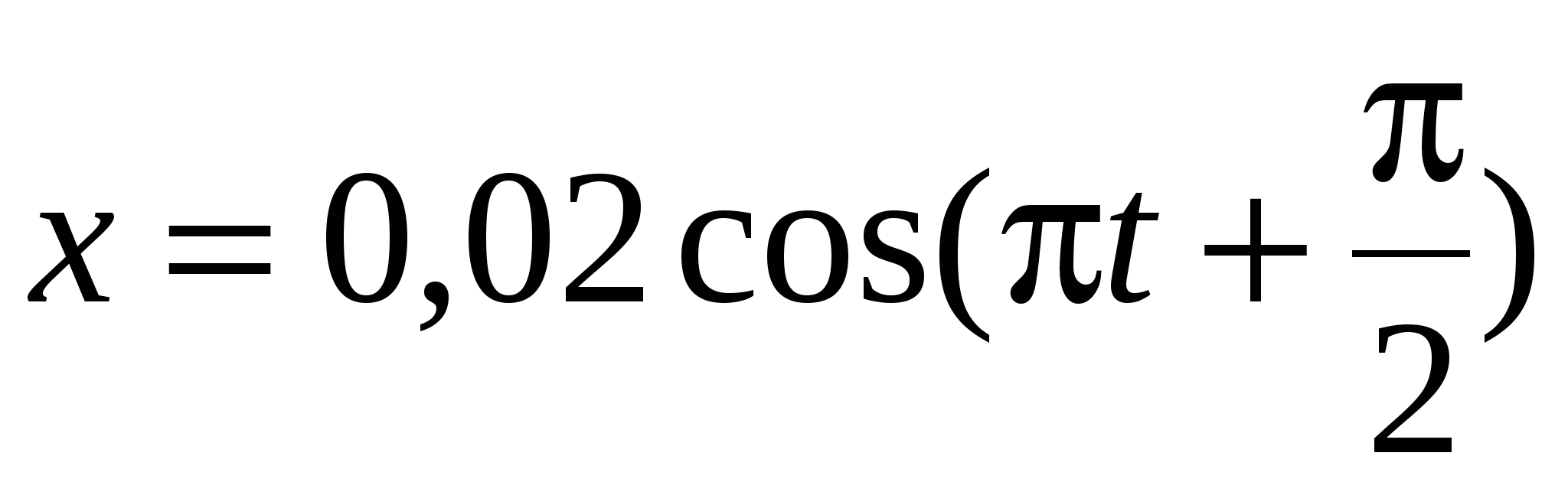 , м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия. Ответ:1) 2 см, 2) 2 с; 3) π/2; 4) 6,28 см/с; 5) 19,7 см/с2; 6) t = m, где m = 0, 1, 2, .... , м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия. Ответ:1) 2 см, 2) 2 с; 3) π/2; 4) 6,28 см/с; 5) 19,7 см/с2; 6) t = m, где m = 0, 1, 2, ....
Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой хо = 5 см, со скоростью υо = 15 см/с. Определить амплитуду колебаний. Ответ: 5,54 см.
Определить максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой А = 3 см и периодом Т = 4 с. Ответ: υmax = 4,71 см/с2; аmax = 7,4 см/с2.
Тело массой m= 10 г совершает гармонические колебания по закону x = 0,1 cos (4πt + π/4) м. Определить максимальные значения: 1) возвращающей силы; 2) кинетической энергии. Ответ:1) 0,158 Н; 2) 7,89 мДж.
Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению 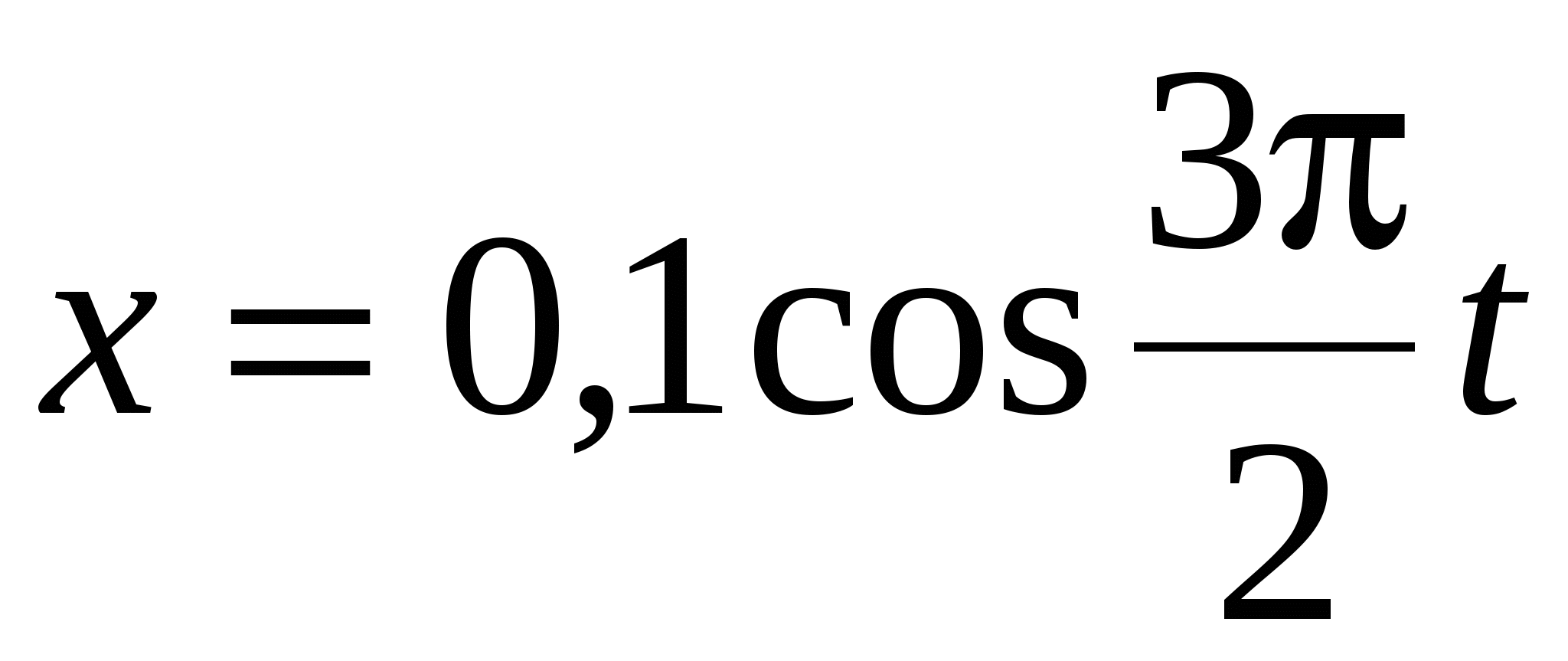 м. Определить: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию E точки. Ответ:1) 78,5 мН; 2) 5,55 мДж. м. Определить: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию E точки. Ответ:1) 78,5 мН; 2) 5,55 мДж.
Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1cos(4πt + π/4) м. Определить полную энергию Е этой точки. Ответ: 15,8 мДж.
Полная энергия Е гармонически колеблющейся точки равна 10 мкДж, а максимальная сила Fmax, действующая на точку, равна -0,5 мН. Написать уравнение движения этой точки, если период Т колебаний равен 4 с, а начальная фаза φ = π/6. Ответ: x = 0,04cos(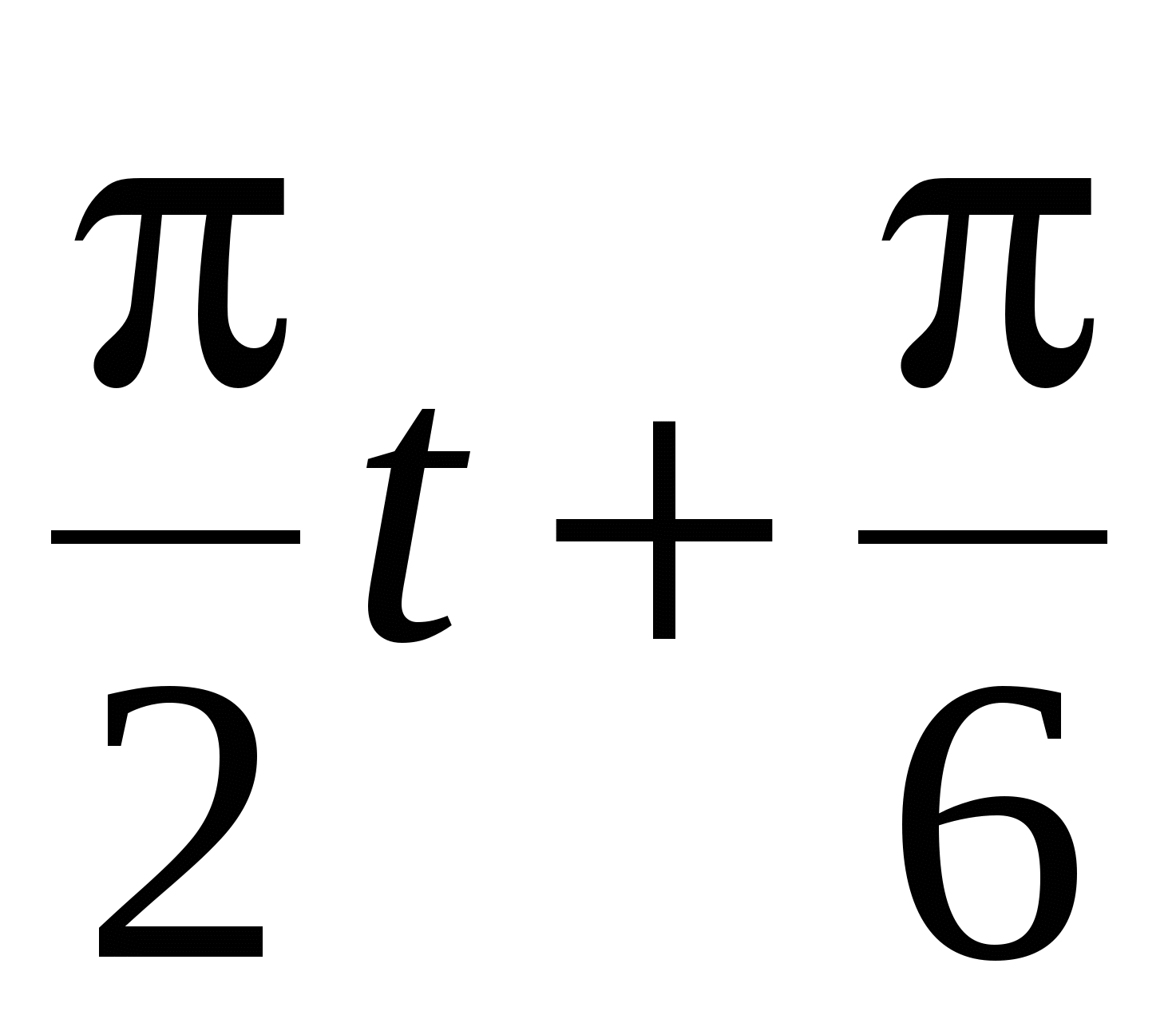 ), м. ), м.
Определить отношение кинетической энергии Т точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания. Ответ: tg2(ω0t + φ).
Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой А = 8 см. Определить жесткость k пружины, если известно, что максимальная кинетическая энергия Тmах груза составляет 0,8 Дж. Ответ: 250 Н/м.
Материальная точка колеблется согласно уравнению x = Acosωt, где А = 5 см и ω = π/12 с-1. Когда возвращающая сила F в первый раз достигает значения — 12мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определить: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt. Ответ:1) 4с; 2) π/3.
Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой А = 6 см. Определить полную энергию E колебаний груза, если жесткость k пружины составляет 500 Н/м. Ответ: 0,9 Дж.
Спиральная пружина обладает жесткостью k = 25 Н/м. Определить, тело какой массой m должно быть подвешено к пружине, чтобы за t = 1 мин совершалось 25 колебаний. Ответ: 3,65 кг.
Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период колебаний груза возрастает в 2 раза. Определить массу первоначально подвешенного груза. Ответ: 0,2 кг.
При подвешивании грузов массами m1 = 600 г и m2 = 400 г к свободным пружинам последние удлинились одинаково (l = 10 см). Пренебрегая массой пружин, определить: 1) периоды колебаний грузов; 2) какой из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз. Ответ: 1) T1 = Т2 = 0,63 с; 2) груз большей массы, в 1,5 раза.
Физический маятник представляет собой тонкий однородный стержень длиной 35 см. Определить, на каком расстоянии от центра масс должна быть точка подвеса, чтобы частота колебаний была максимальной. Ответ: 10,1 см.
Однородный диск радиусом R = 20 см колеблется около горизонтальной оси, проходящей на расстоянии l = 15 см от центра диска. Определить период Т колебаний диска относительно этой оси. Ответ: 1,07 с.
Тонкий обруч радиусом R = 50 см подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Определить период Т колебаний обруча. Ответ: 2 с.
Тонкий однородный стержень длиной l = 60 см может свободно вращаться вокруг горизонтальной оси, проходящей через верхний конец стержня. Стержень отклонили на угол αo = 0,01 рад и в момент времени t0 = 0 отпустили. Считая колебания малыми, определить период колебаний стержня и записать функцию α(t). Ответ: 1,27 с, α(t) = 0,01 cos1,57πt рад.
Тонкий однородный стержень длиной l = 60 см может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии x = 15 см от его середины. Определить период колебаний стержня, если он совершает малые колебания. Ответ: 2,2 с.
Математический маятник, состоящий из нити длиной l = 1 м и свинцового шарика радиусом r = 2 см, совершает гармонические колебания с амплитудой А = 6 см. Определить: 1) скорость шарика при прохождении им положения равновесия; 2) максимальное значение возвращающей силы. Плотность свинца ρ = 11,3 г/см3. Ответ:1) 0,186 м/с; 2) 69,5 мН.
Два математических маятника имеют одинаковые массы, длины, отличающиеся в n = 1,5 раза, и колеблются с одинаковыми угловыми амплитудами. Определить, какой из маятников обладает большей энергией и во сколько раз. Ответ: Маятник большей длины, в 1,5 раза.
Два математических маятника, длины которых отличаются на Δl = 16 см, совершают за одно и то же время один n1 = 10 колебаний, другой — n2 = 6 колебаний. Определить длины маятников l1 и l2. Ответ: l1 = 9 см, l2 = 25 см.
Математический маятник длиной l = 50 см подвешен в кабине самолета. Определить период Т колебаний маятника, если самолет движется: 1) равномерно; 2) горизонтально с ускорением a = 2,5 м/с2. Ответ:1) 1,42 с; 2) 1,4 с.
Математический маятник длиной l = 1 м подвешен к потолку кабины, которая начинает опускаться вертикально вниз с ускорением a1 = g/4. Спустя время t1 = 3 с после начала движения кабина начинает двигаться равномерно, а затем в течение 3 с тормозится до остановки. Определить: 1) периоды Т1, Т2, Т3 гармонических колебаний маятника на каждом из участков пути; 2) период T4 гармонических колебаний маятника при движении точки подвеса в горизонтальном направлении с ускорением а4 = g/4. Ответ: Т1 = 2,32 с, Т2 = 2,01 с, Т3= 1,79 с, Т4 = 0,621 с.
Два одинаково направленных гармонических колебания одинакового периода с амплитудами А1 = 4 см и А2 = 8 см имеют разность фаз φ = 45°. Определить амплитуду результирующего колебания. Ответ: 11,2 см.
Амплитуда результирующего колебания, получающегося при сложении двух одинаково направленных гармонических колебаний одинаковой частоты, обладающих разностью фаз φ = 60°, равна А = 6 см. Определить амплитуду А2 второго колебания, если A1 = 5 cм. Ответ: 1,65 см.
Определить разность фаз двух одинаково направленных гармонических колебаний одинаковых частоты и амплитуды, если амплитуда их результирующего колебания равна амплитудам складываемых колебаний. Ответ:120°.
Разность фаз двух одинаково направленных гармонических колебаний одинакового периода Т = 4 с и одинаковой амплитуды А = 5 см составляет π/4. Написать уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю. Ответ: 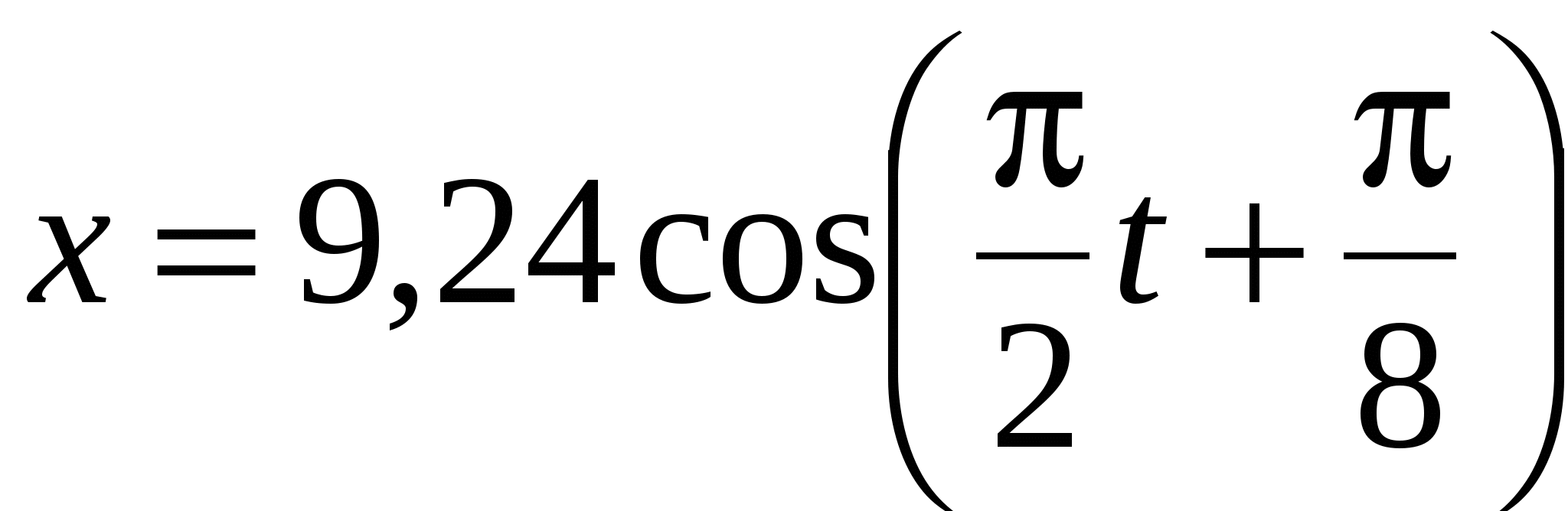 , см. , см.
Складываются два гармонических колебания одного направления, описываемых уравнениями х1 = 3cos2πt см и x2 = 3соs(2πt+ π/4) см. Определить для результирующего колебания: 1) амплитуду; 2) начальную фазу. Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд. Ответ: 1) 5,54 см; 2) π/8; 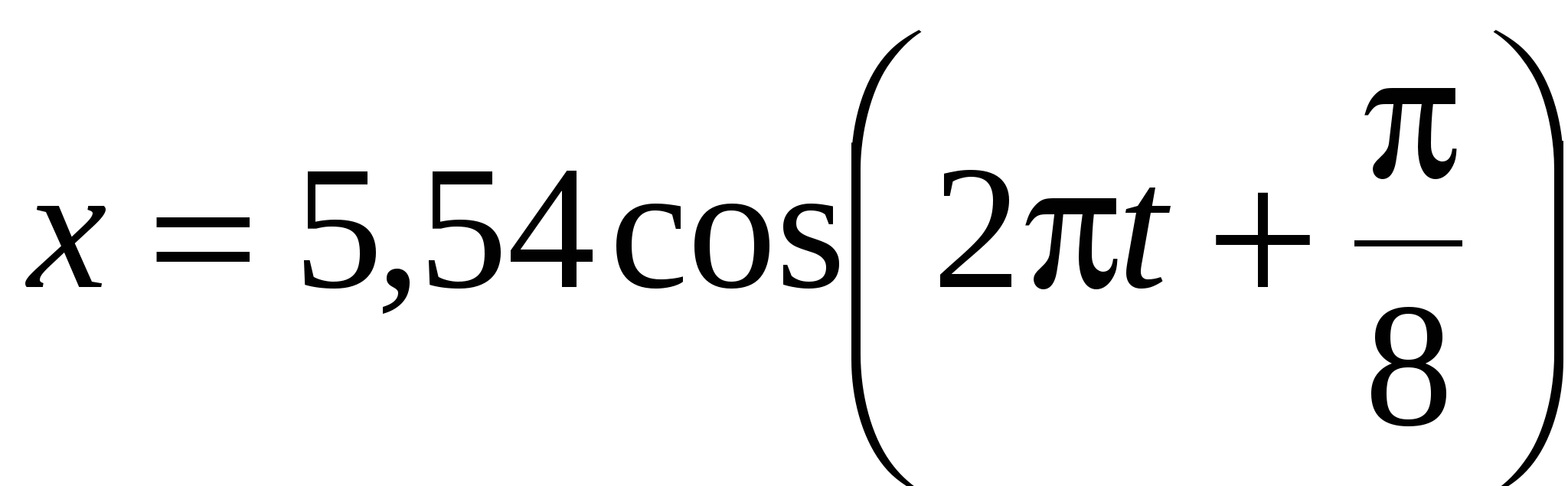 , см. , см.
Частоты колебаний двух одновременно звучащих камертонов настроены соответственно на 560 и 560,5 Гц. Определить период биений. Ответ: 2 с.
В результате сложения двух колебаний, период одного из которых t1 = 0,02 с, получают биения с периодом Тб = 0,2 с. Определить период Т2 второго складываемого колебания. Ответ: 22,2 мс.
Складываются два гармонических колебания одного направления, имеющие одинаковые амплитуды и одинаковые начальные фазы, с периодами Т1 = 2 с и Т2 = 2,05 с. Определить: 1) период результирующего колебания; 2) период биения. Ответ: 1) 2,02 с; 2) 82 с.
Результирующее колебание, получающееся при сложении двух гармонических колебаний одного направления, описывается уравнением вида x = Acos t cos 45t (t — в секундах). Определить: 1) циклические частоты складываемых колебаний; 2) период биений результирующего колебания. Ответ:1) ω1 = 46 c-1, ω2 = 45 с-1; 2) Т = 6,28 с.
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = 3cosωt, см и у = 4cosωt, см. Определить уравнение траектории точки и вычертить ее с нанесением масштаба. Ответ: y= 4х/3.
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = 3cos2ωt, см и у = 4cos(2ωt + π), см. Определить уравнение траектории точки и вычертить ее с нанесением масштаба. Ответ: у= –4х/3.
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = Asin ωt и y = Bcos ωt, где А, В и ω — положительные постоянные. Определить уравнение траектории точки, вычертить ее с нанесением масштаба, указав направление ее движения по этой траектории. Ответ: х2/А2 + у2/В2 = 1, по часовой стрелке.
Точка участвует одновременно в двух гармонических колебаниях одинаковой частоты, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями х= Asin(ωt + π/2) и y = Asin ωt. Определить уравнение траектории точки и вычертить ее с нанесением масштаба, указав направление ее движения по этой траектории. Ответ: х2 + у2 = А2, против часовой стрелки.
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x= cos 2πt и у = cos πt. Определить уравнение траектории точки и вычертить ее с нанесением масштаба Ответ: 2у2 –х= 1.
Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = Asinωt и у = Asin2ωt. Определить уравнение траектории точки и вычертить ее с нанесением масштаба. Ответ: у2 = 4х2(1–х2/А2).
Период затухающих колебаний Т = 1 с, логарифмический декремент затухания Θ = 0,3, начальная фаза равна нулю. Смещение точки при t = 2 Т составляет 5см. Записать уравнение движения этого колебания. Ответ: x = 9,l·e-0,3t cos2πt, см.
Амплитуда затухающих колебаний маятника за t = 2 мин уменьшилась в 2 раза. Определить коэффициент затухания δ. Ответ: 5,78·10-3 с-1.
Логарифмический декремент колебаний Θ маятника равен 0,01. Определить число N полных колебаний маятника до уменьшения его амплитуды в 3 раза. Ответ: 110.
Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась в 3 раза. Определить, во сколько раз она уменьшится за 4 мин. Ответ: В 81 раз.
Начальная амплитуда затухающих колебаний маятника аo = 3 см. По истечении t1 = 10 с A1 = 1 см. Определить, через сколько времени амплитуда колебаний станет равной А2 = 0,3 см. Ответ: 21 с.
Тело массой m = 0,6 кг, подвешенное к спиральной пружине жесткостью k = 30 Н/м, совершает в некоторой среде упругие колебания. Логарифмический декремент колебаний Θ = 0,01. Определить: 1) время t, за которое амплитуда колебаний уменьшится в 3 раза; 2) число N полных колебаний, которые должна совершить гиря, чтобы произошло подобное уменьшение амплитуды. Ответ: 1) 97,6 с; 2) 110.
При наблюдении затухающих колебаний выяснилось, что для двух последовательных колебаний амплитуда второго меньше амплитуды первого на 60 %. Период затухающих колебаний Т = 0,5 с. Определить: 1) коэффициент затухания δ; 2) для тех же условий частоту νo незатухающих колебаний. Ответ:1) δ=1,83с-1; 2) 2,02 Гц.
Тело массой m = 100 г, совершая затухающие колебания, за τ = 1 мин потеряло 40 % своей энергии. Определить коэффициент сопротивления r. Ответ: 8,51 ·10-4 кг/с.
За время, в течение которого система совершает N= 50 полных колебаний, амплитуда уменьшается в 2 раза. Определить добротность Q системы. Ответ: 227.
Частота свободных колебаний некоторой системы ω = 65 рад/с, а ее добротность Q = 2. Определить собственную частоту ωo колебаний этой системы. Ответ: 67 рад/с.
Определить резонансную частоту колебательной системы, если собственная частота колебаний νo = 300 Гц, а логарифмический декремент Θ = 0,2. Ответ: 300 Гц.
Собственная частота νo колебаний некоторой системы составляет 500 Гц. Определить частоту ν затухающих колебаний этой системы, если резонансная частота νрез = 499 Гц. Ответ: 499,5 Гц.
Период затухающих колебаний системы составляет 0,2 с, а отношение амплитуд первого и шестого колебаний равно 13. Определить резонансную частоту данной колебательной системы. Ответ: 4,97 Гц.
Определить разность фаз Δφ колебаний двух точек, лежащих на луче и друг от друга на расстоянии Δl = 1 м, если длина волны λ = 0,5м. Ответ: Δφ = 4π, точки колеблются в одинаковых фазах.
Две точки лежат на луче и находятся от источника колебаний на расстояниях х1 = 4 м и х2 = 7 м. Период колебаний Т = 20 мс и скорость н распространения волны равна 300 м/с. Определить разность фаз колебаний этих точек. Ответ: Δφ =π , точки колеблются в противоположных фазах.
Волна распространяется в упругой среде со скоростью υ = 150 м/с. Определить частоту н колебаний, если минимальное расстояние Δx между точками среды, фазы колебаний которых противоположны, равно 0,75 м. Ответ: 100 Гц.
Определить длину волны λ, если числовое значение волнового вектора k равно 0,02512 см-1. Ответ: 2,5 м.
Звуковые колебания с частотой ν = 450 Гц и амплитудой А= 0,3 мм распространяются в упругой среде. Длина волны λ = 80 см. Определить: 1) скорость распространения волн; 2) максимальную скорость частиц среды. Ответ: 1) 360 м/с; 2) 84,8 см/с.
Два когерентных источника колеблются в одинаковых фазах с частотой ν = 400 Гц. Скорость распространения колебаний в среде υ = 1 км/с. Определить при какой наименьшей разности хода будет наблюдаться: 1) максимальное усиление колебаний; 2) максимальное ослабление колебаний. Ответ:1) 2,5 м; 2) 1,25 м.
Два когерентных источника посылают поперечные волны в одинаковых фазах. Периоды колебаний Т = 0,2 с, скорость распространения волн в среде υ = 800 м/с. Определить, при какой разности хода в случае наложения волн будет наблюдаться: 1) ослабление колебаний; 2) усиление колебаний. Ответ: 1) ±80(2m+l), м (m = 0, 1, 2, ...); 2) ± 160m, м (m = 0, 1, 2, ...).
Два динамика расположены на расстоянии d = 0,5 м друг от друга и воспроизводят один и тот же музыкальный тон на частоте ν = 1500 Гц. Приемник находится на расстоянии l = 4 м от центра динамиков. Принимая скорость звука υ = 340 м/с, определить на какое расстояние от центральной линии параллельно динамикам надо отодвинуть приемник, чтобы он зафиксировал первый интерференционный минимум. Ответ: 90,7 см.
Определить длину волны λ, если расстояние Δ1 между первым и четвертым узлами стоячей волны равно 30 см. Ответ: 20 см.
Для определения скорости звука в воздухе методом акустического резонанса используется труба с поршнем и звуковой мембраной, закрывающей один из ее торцов. Расстояние между соседними положениями поршня, при котором наблюдается резонанс на частоте ν = 2500 Гц, составляет l = 6,8 см. Определить скорость звука в воздухе. Ответ: 340 м/с.
|
 Скачать 0.66 Mb.
Скачать 0.66 Mb.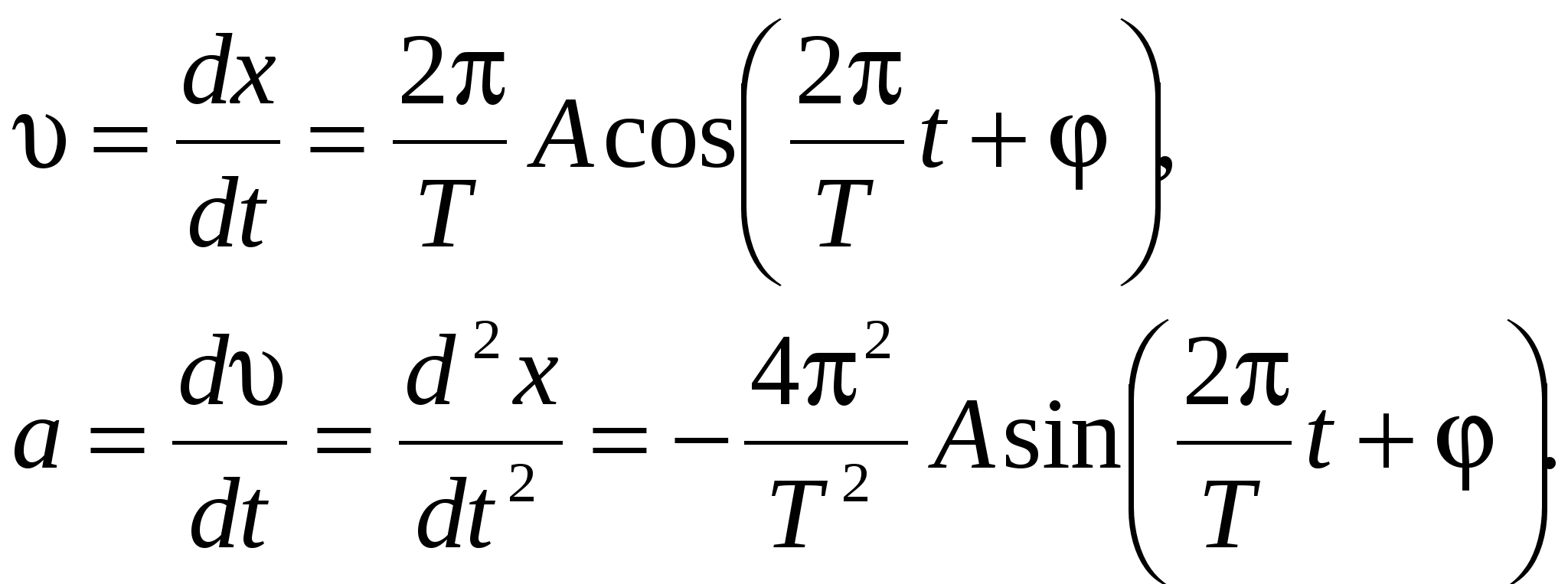
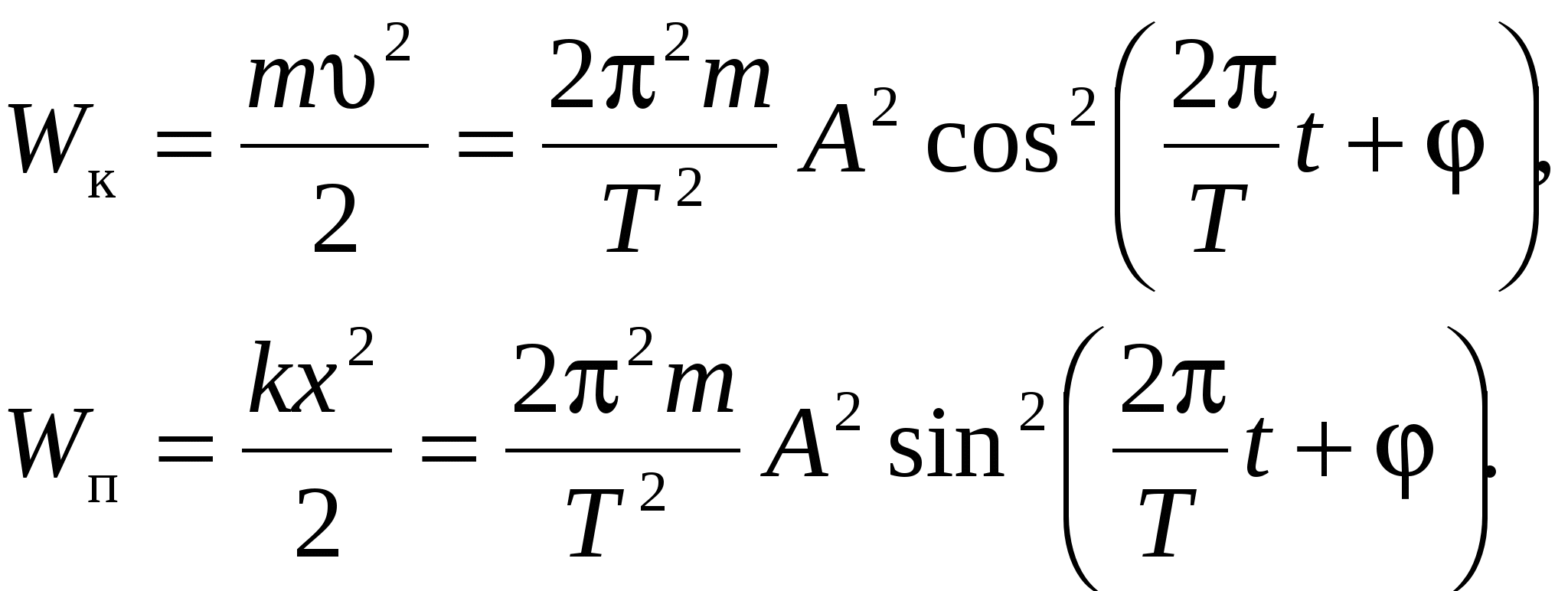
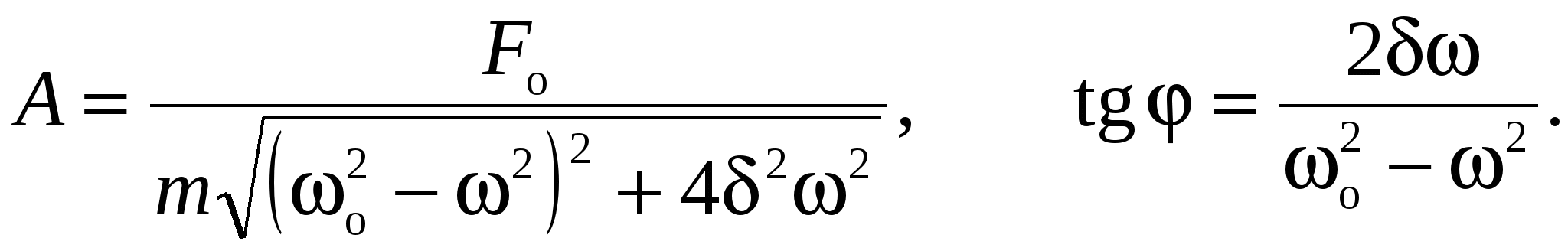
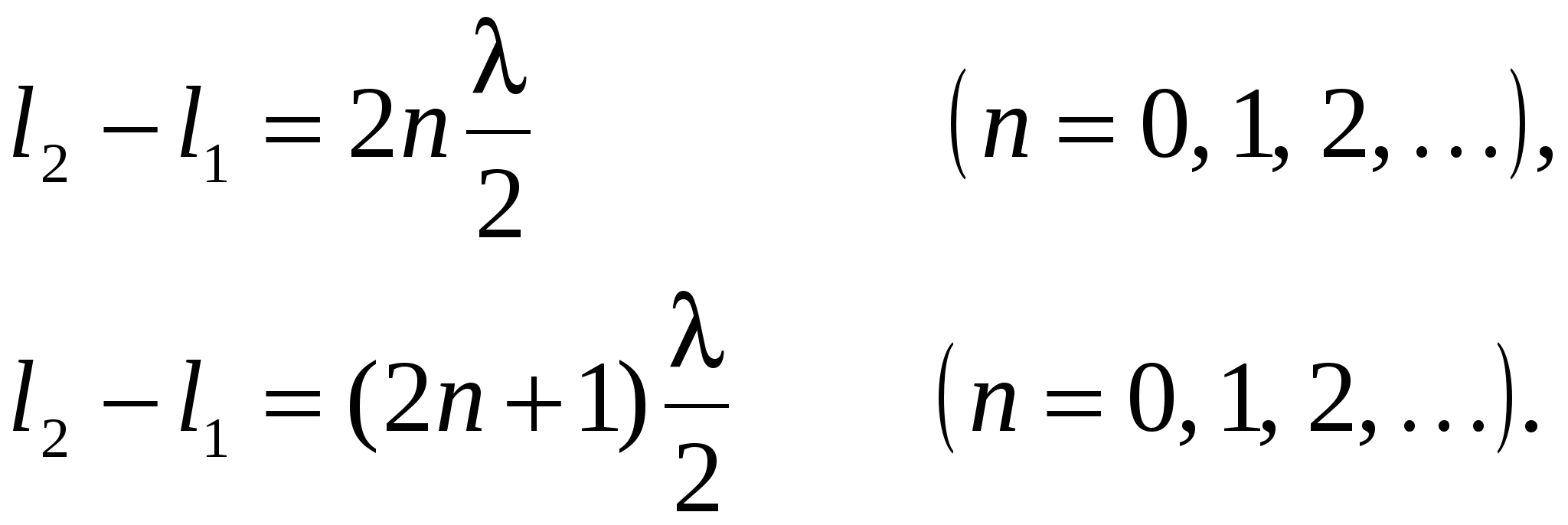

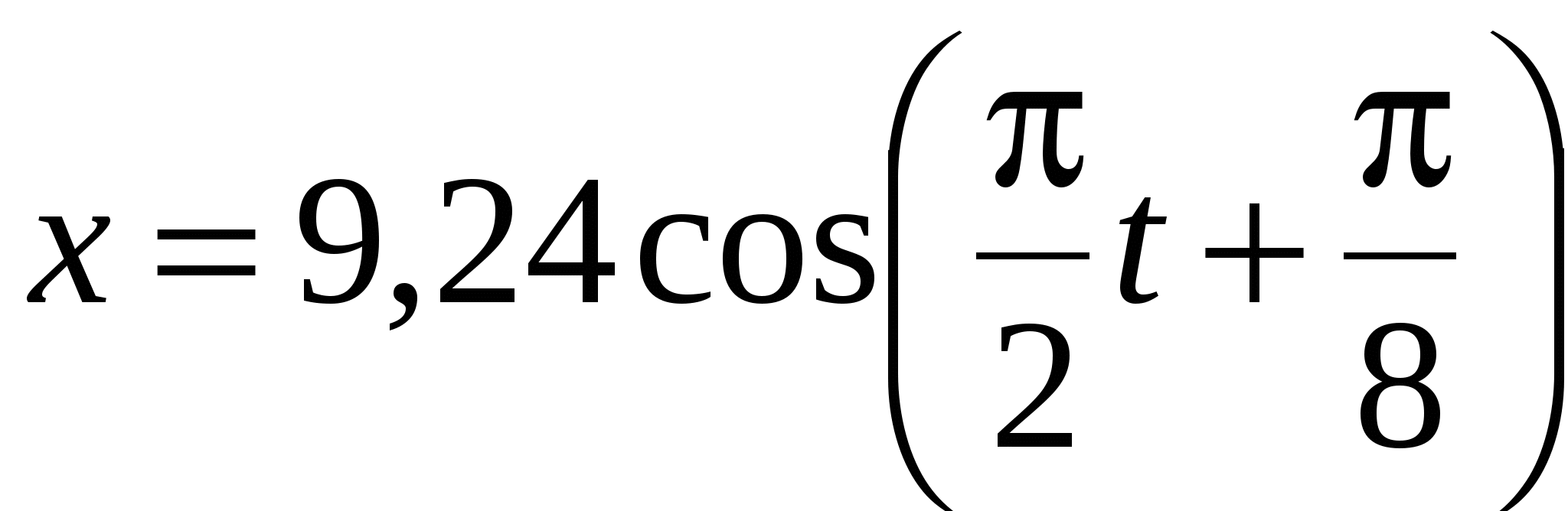 , см.
, см.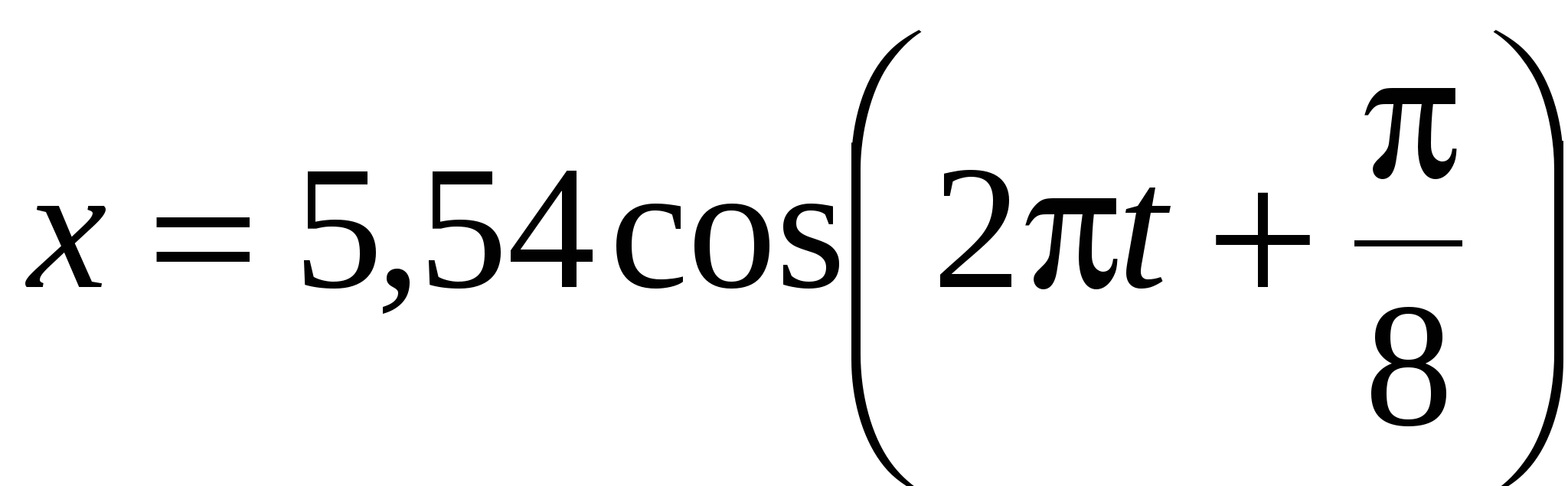 , см.
, см.