ргр. Уфимский государственный нефтяной технический университет
 Скачать 399.59 Kb. Скачать 399.59 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Уфимский государственный нефтяной технический университет Кафедра электротехники и электрооборудования предприятий Расчетно-графическая работа №1 «Электрическое, магнитное и электромагнитное поля двухпроводной линии» Вариант № 3 Выполнил: студент группы БАЭ-16-01 Быков Г.О. Проверил: канд. тех. наук, доцент Чигвинцев С.В. Уфа, 2022 Содержание
Исходные данные У двухпроводной линии (рисунок 1) два длинных параллельных проводника 1 и 2 проводимостью γП и диаметром d расположены в среде с относительной диэлектрической проницаемостью ε параллельно проводящей полуплоскости (оси Z), проводимость которой γЗ. Положение проводников задано координатами в плоскости поперечного сечения XY. К началу линии подключен источник ЭДС E, напряжение U на зажимах которого симметрично относительно проводящей полуплоскости. 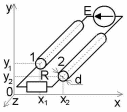 Рисунок 1 – Схема двухпроводной линии Таблица 1 – Исходные данные
1 Расчет электрического поля Поскольку провода находятся над проводящей полуплоскостью, то задача решается с использованием методов зеркальных изображений и наложения. Наведенные на поверхности проводящей полуплоскости заряды могут быть представлены фиктивными зарядами с линейной плотностью –τ1 и –τ2, расположенными зеркально относительно оси абсцисс с ординатами –у1 и –у2, величина которых равна реальным τ1 и τ2, а знаки противоположны. На рисунке 2 показано направление векторов смещения при условии, что провод 1 несет положительный заряд с линейной плотностью заряда τ1, а провод 2 – отрицательный τ2. 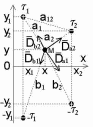 Рисунок 2 Результирующее электрическое поле (смещение D) в верхней полуплоскости может быть представлено как суперпозиция полей векторов смещения (Da1, Da2, Db1 и Db2) соответственно четырех зарядов (τ1, τ2, −τ1 и −τ2) D = Da1 + Da2 + Db1 + Db2. (2.1) Направлены векторы Da1 и Db2 и по прямой из точки М от положительных зарядов τ1 и τ2, а векторы Da2 и Db1 - к отрицательным −τ1 и −τ2. Если согласно теореме Гаусса 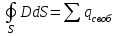 , (2.2) , (2.2)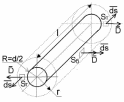 Рисунок 3 охватить провод замкнутой поверхностью, состоящей из боковой цилиндрической поверхности Sб и двух торцевых поверхностей в виде кругов Sт, радиусом r (рисунок 3), то правая часть уравнения (2.2) представит сумму трех потоков 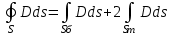 . (2.3) . (2.3)Поскольку угол между вектором-площадкой ds и вектором смещения D на торцевых поверхностях составляет 900, то поток вектора смещения будет только через боковую цилиндрическую поверхность площадью 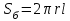 . (2.4) . (2.4)Сумма зарядов, находящихся внутри замкнутой поверхности, определяется через линейную плотность заряда τ и длину провода l 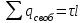 (2.5) (2.5)С учетом (2.3) и (2.5) уравнение (2.2) примет вид 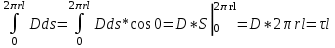 (2.6) (2.6)Из (2.6) зависимость D=f(r) 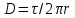 (2.7) (2.7)Поскольку 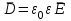 (2.8) (2.8)то 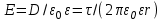 . (2.9) . (2.9)1.1 Потенциал проводов φ1=U/2=150/2=75 В φ2=-U/2=-150/2=-75 В. Расстояния между реальными и фиктивными проводниками. Если точку наблюдения М (рисунок 2) поместить на поверхность первого проводника радиусом R1 с потенциалом φ1, то 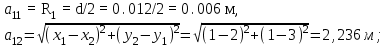 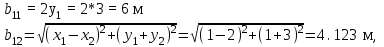 (2.20) (2.20)а затем на поверхность второго радиусом R2 с потенциалом φ1: 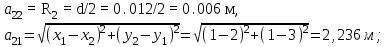 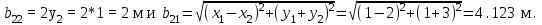 (2.21) (2.21)Уравнение (2.19) с учетом (2.20) и (2.21) для точек наблюдения на поверхностях первого и второго проводника примет вид 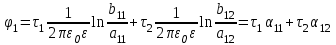 ; (2.22) ; (2.22)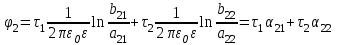 , (2.23) , (2.23)где в уравнениях (2.22) и (2.23) собственные аii и взаимные аij= аji потенциальные коэффициенты. 1.2 Потенциальные и емкостные коэффициенты, частичные емкости Потенциальные коэффициенты: 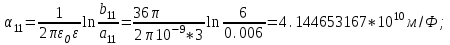 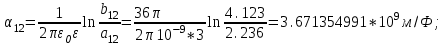 (2.24) (2.24)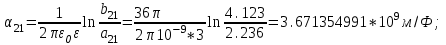 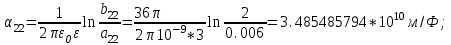 Система уравнений 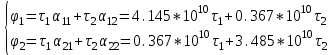 (2.25) (2.25)носит название первой группы формул Максвелла. Решение этой системы в системе Maple 11 дает следующие результаты  = 2.019*10-9 Кл/м и τ2 = −2.365*10-9 Кл/м. (2.26) = 2.019*10-9 Кл/м и τ2 = −2.365*10-9 Кл/м. (2.26)Вторая группа формул Максвелла получается в результате решения системы уравнений (2.25) относительно τ1 и τ2 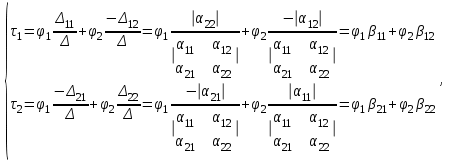 (2.27) (2.27)где: βij – емкостные коэффициенты ([β]=Ф/м); ∆ – главный определитель системы; ∆ij – алгебраические дополнения (миноры). Емкостные коэффициенты: 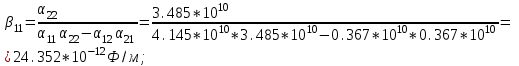 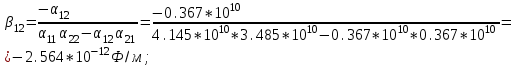 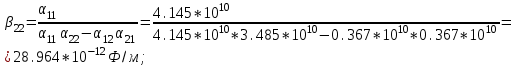 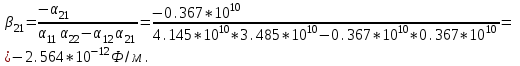 (2.28) После несложных преобразований система уравнений (2.27) примет вид третей группы формул Максвелла 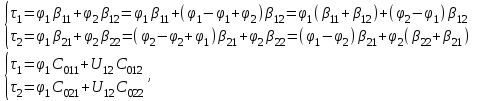 (2.29) где: С0ii=βii+βij и С0ij= С0ji= −βij – собственные и взаимные погонные емкости проводов Частичные емкости: 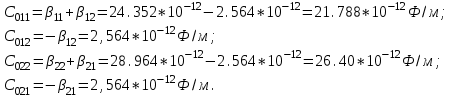 (2.30) (2.30)1.3 Электрическое смещение и напряженность электрического поля 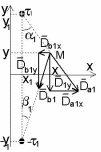 Рисунок 4 Проекции векторов Da1 и Db1 смещения на оси координат (рисунки 2 и 4) 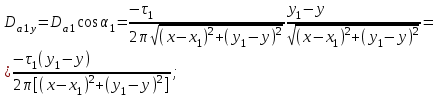 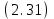 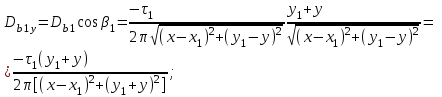 (2.32) (2.32)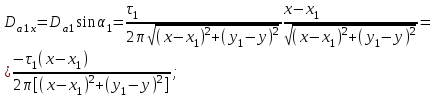 (2.33) (2.33)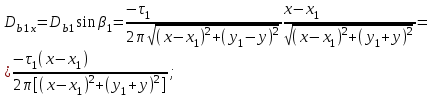 (2.34) (2.34)Проекции векторов смещения от заряда первого провода и его изображения 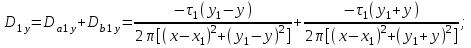 (2.35) (2.35)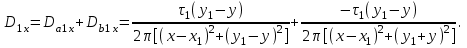 (2.36) (2.36)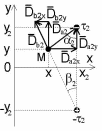 Рисунок 5 Проекции векторов смещения Da2 и Db2 на оси координат (рисунки 2 и 5) 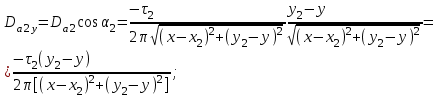 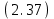 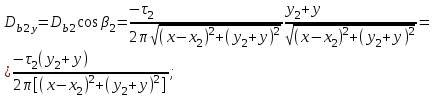 (2.38) (2.38)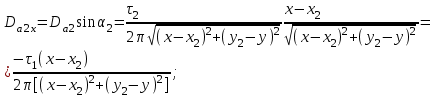 (2.39) (2.39)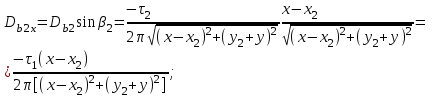 (2.40) (2.40)Проекции векторов смещения от заряда второго провода и его изображения 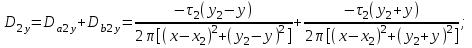 (2.41) (2.41)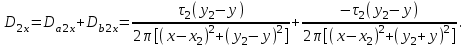 (2.42) (2.42)Проекции векторов смещения от двух проводников и их изображений 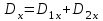 и и 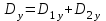 , ,а также модуль смещения 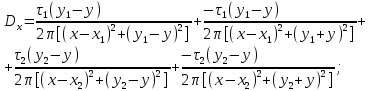 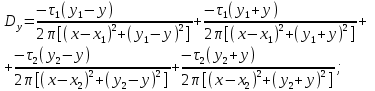 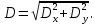 Напряженности электрического поля Поскольку D=ε0εЕ, то Е=D/ε0ε= τ/(2πε0εr), следовательно: E1x=D1x/ε0ε ; E2x=D2x/ε0ε ; E1y=D1y/ε0ε ; E2y=D2y/ε0ε ; Ex=Dx/ε0ε ; Ey=Dy/ε0ε . 1.4 Зависимость потенциала φ от координат ХУ. В силу цилиндрической симметрии параметры электрического поля (D, E и φ) изменяются только по радиусу. Из связи напряженности электрического поля с потенциалом через градиент 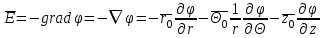 (2.10) (2.10)следует, что с учетом (2.9) 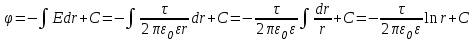 (2.11) (2.11)Постоянная интегрирования С определяется из условия, что потенциал проводящей полуплоскости равен нулю φу=0=0. По методу наложения, также как и для смещения (2.1) можно записать уравнения для напряженностей электрического поля 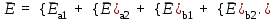 (2.12) (2.12)и электрического потенциала 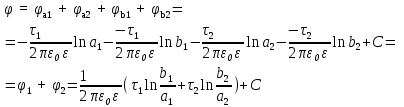 (2.13) (2.13)При у=0 потенциал φ=0, а a1=b1 и a2=b2 и постоянная интегрирования С из (2.13) 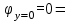 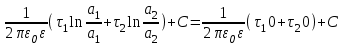 (2.14) (2.14)будет равна нулю С=0. Радиусы a1, a2, b1 и b2, соединяющие точку наблюдения М (рисунок 2) с реальными (1 и 2) и фиктивными (-1 и -2) проводниками, будут соответственно равны 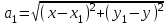 ; (2.15) ; (2.15)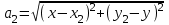 ; (2.16) ; (2.16)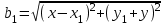 ; (2.17) ; (2.17)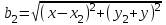 . (2.18) . (2.18)Окончательно функция потенциала (2.13) от координат ХУ в верхней полуплоскости с учетом равенства нулю постоянной интегрирования и формул (2.15) – (2.18) примет вид 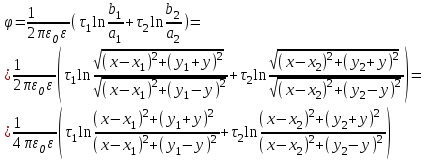 (2.19) (2.19)1.5 Диаграммы зависимостей от координат электрического смещения (D1x, D2x, D1у, D2у), напряженности поля (Еx, Еу, Е) и потенциала. Таблица 2 – Значение вычисленных параметров при y = 0 м
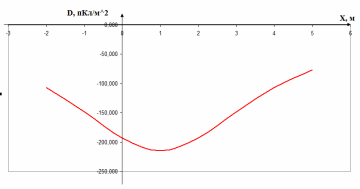 Рисунок 6 – Диаграмма D1y 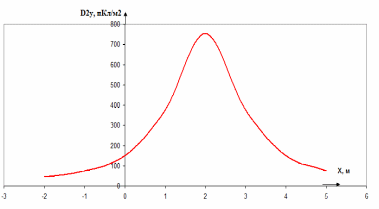 Рисунок 7 – Диаграмма D2y 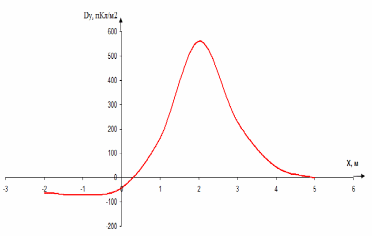 Рисунок 8 – Диаграмма Dy 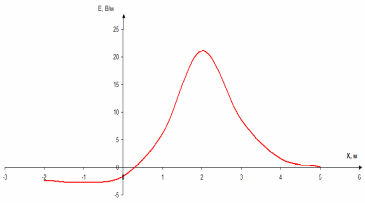 Рисунок 9 – Диаграмма Ey 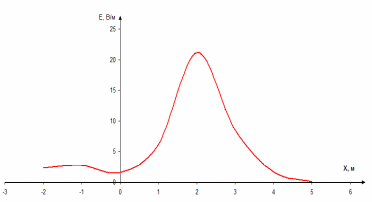 Рисунок 10 – Диаграмма E 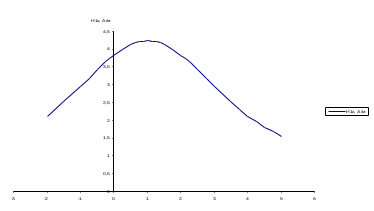 Рисунок 11 – Диаграмма H1x Р 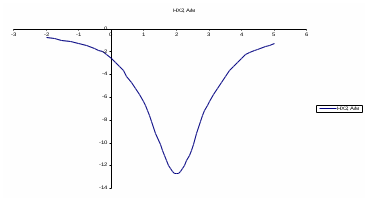 исунок 12 – Диаграмма H2x исунок 12 – Диаграмма H2xР 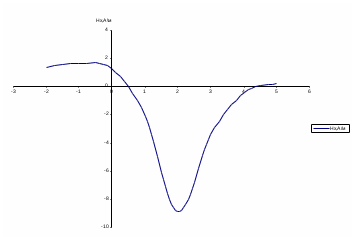 исунок 13 – Диаграмма Hx исунок 13 – Диаграмма Hx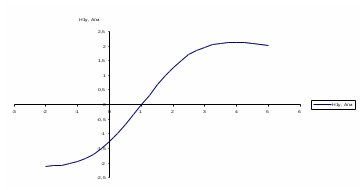 Рисунок 14 – Диаграмма H1y 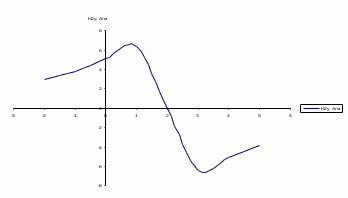 Рисунок 15 – Диаграмма H2y Рисунок 16 – Диаграмма Hy 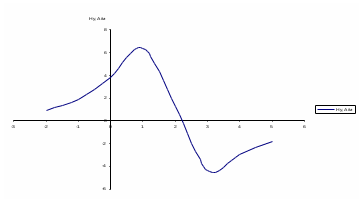 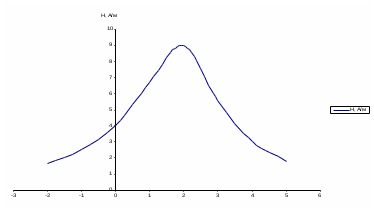 Рисунок 17 – Диаграмма H Рисунок 18 – Диаграмма B 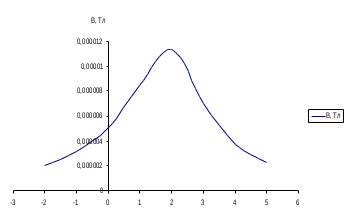 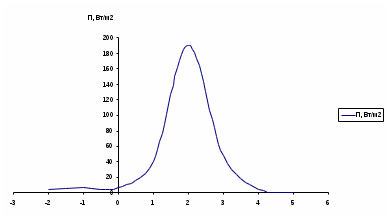 Рисунок 19 – Диаграмма П Сила электрического поля, действующая на проводники с зарядами на единицу длины F01Э и F02Э.Пондеромоторная сила электрического поля на единицу длины F01Э и F02Э. 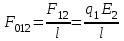 Так как 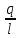 - это линейная плотность заряда τ, то формула запишется в виде - это линейная плотность заряда τ, то формула запишется в виде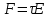 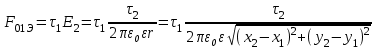 ; ;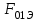 = 2.019* = 2.019*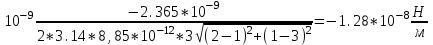 . .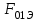 = =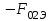 , , 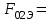 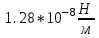 . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
