ЛАБА 4. Поле длинной двухпроводной линии
 Скачать 37.66 Kb. Скачать 37.66 Kb.
|
|
потенциальны (не образуют вихрей в пространстве, окружающем электроды), а во-вторых, как линии напряженности электростатического поля, так и линии тока перпендикулярны линиям или поверхностям равного потенциала.  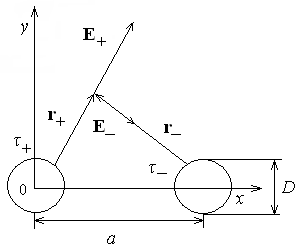 Рис. 4.2 Поле длинной двухпроводной линии. На планшете моделируются так называемые плоские поля, т. е. такие поля, картина которых остается неизменной при параллельном переносе плоскости, в которой производится исследование поля. Как правило, это электростатические поля объектов, бесконечно протяженных в направлении, перпендикулярном секущей плоскости. В работе исследуется поле двух длинных, параллельных, равномерно и разноименно заряженных проводящих цилиндров (двухпроводной линии). Если абсолютное значение линейной плотности заряда на цилиндрах (Кл/м), то напряженность электростатического поля в произвольной точке секущей плоскости будет определяться геометрической суммой напряженностей полей, создаваемых каждым цилиндром (принцип суперпозиции). Для каждого цилиндра абсолютное значение напряженности поля 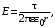 (4.3) (4.3)а значение и направление результирующего вектора напряженности поля определяют по отношению к системе координат x0y (рис. 4.2), которую задает экспериментатор. Напряженность поля и вектор индукции. Для электростатического поля справедливо следующее соотношение между векторами напряженности поля и электрической индукции: 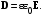 (4.4) (4.4)Особенность вектора электрической индукции состоит в том, что, описывая с помощью этой физической величины электрическое поле, исследователь избавляется от необходимости учитывать связанные заряды, возникающие при поляризации среды. Поток вектора индукции электрического поля (теорема Гаусса).Поток вектора индукции электрического поля определяется выражением 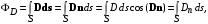 (4.5) (4.5)где S – поверхность произвольной формы в области поля; n – единичный вектор нормали в данной точке поверхности. Поток вектора индукции поля служит характеристикой источников этого поля. Для электростатического поля справедлива теорема Гаусса 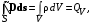 (4.6) (4.6)где S – произвольная 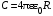 Для плоского, цилиндрического и сферического конденсаторов их электроемкости определяются, соответственно, как 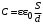 , , 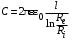 , , 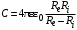 , ,где S – площадь пластины плоского конденсатора; d – расстояние между пластинами; l – длина цилиндрического конденсатора; Re, Ri – радиусы внешней и 5. Выведите выражение для энергии электрического поля, заключенного внутри равномерно заряженного с объемной плотностью шара, имеющего радиус R и диэлектрическую проницаемость . Указания по выполнению наблюдений 1. Выполнить эскиз модели. Для этого, пользуясь подвижными линейками планшета, определить координаты и размеры электродов модели. Нанести изображения электродов и оси координат на подготовленный бланк между электродами. 3. Установить одну из линеек таким образом, чтобы щуп перемещался вдоль линии, соединяющей центры электродов. Перемещая другую линейку, измерить потенциал в двух различных точках модели, расположенных на расстоянии 0.5 см вдоль этой линии. 4. Наметить на эскизе модели произвольный контур, охватывающий электроды, таким образом, чтобы размеры контура на модели составляли примерно 3 × 6 см. Разбить контур на отрезки, длина которых на потока вектора индукции в данной области, исходя из того, что диэлектрическая проницаемость моделируемой области = 1. Вычислите значение моделируемого заряда (линейную плотность), используя известное значение разности потенциалов между электродами, рассчитайте электроемкость. Сравните полученное значение с рассчитанным в п. 2 «Указаний по выполнению наблюдений», а также с результатом вычислений п. 2 «Задания на подготову к работе». 4. Сформулируйте выводы по проведенному исследованию. |
