Задание_1_2. Задание Расчет напряженностей и потенциалов электрических полей
 Скачать 21.19 Kb. Скачать 21.19 Kb.
|
|
Задание 1. Расчет напряженностей и потенциалов электрических полей Бесконечная плоская плита, толщиной а равномерно заряжена по объему с плотностью ρ. Найти потенциал и напряженность электрического поля. Бесконечно длинный круговой цилиндр радиуса R равномерно заряжен по объему так, что на единицу его длины приходится заряд τ. Найти потенциал и напряженность электрического поля. Бесконечно длинный круговой цилиндр радиуса R равномерно заряжен по поверхности так, что на единицу его длины приходится заряд τ. Найти потенциал и напряженность электрического поля. Найти потенциал и напряженность электрического поля равномерно заряженной прямолинейной бесконечно длинной нити как функцию расстояния r от нити. На единицу длины нити приходится заряд τ. Найти потенциал и напряженность отрезка длины 2а с зарядом q как функцию расстояния от центра стержня до точки прямой, перпендикулярной к стержню и проходящей через его центр. Найти потенциал и напряженность электрического поля шара, равномерно заряженного по объему. Радиус шара R, заряд q. Тонкое круглое кольцо радиуса состоит из равномерно и противоположно заряженных полуколец с зарядами q и –q. Найти потенциал кольца на оси кольца. Найти потенциал и напряженность электрического поля на оси равномерно заряженного круглого тонкого диска радиуса R; заряд диска q. Плоскости двух тонких коаксиальных равномерно заряженных колец одинакового радиуса R находятся на расстоянии а друг от друга. Работа, которую на до совершить, чтобы перенести точечный заряд из бесконечности в центр каждого из колец, равна соответственно А1 и А2. Найти заряды на кольцах q1 и q2. Сфера радиуса r заряжена с поверхностной плотностью 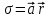 , где , где 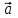 –постоянный вектор, –постоянный вектор, 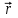 – радиус-вектор точки сферы относительно ее центра. Найти напряженность электрического поля в центре сферы. – радиус-вектор точки сферы относительно ее центра. Найти напряженность электрического поля в центре сферы.Задание 2. Электростатика диэлектриков и проводников. Плоский конденсатор заполнен диэлектриком, проницаемость которого изменяется по закону ε=ε0(х+а)/а, где а – расстояние между обкладками конденсатора, ось х направлена перпендикулярно обкладкам, S – площадь обкладки. Найти емкость конденсатора, пренебрегая емкостными коэффициентами и распределение связанных зарядов, если к обкладкам приложена разность потенциалов U. Точечный заряд q находится на плоскости, отделяющей вакуум от безграничного однородного диэлектрика с проницаемостью ε. Найти модули векторов 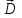 и и 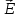 и потенциал φ как функции расстояния r от заряда q. и потенциал φ как функции расстояния r от заряда q.В плоский конденсатор, расстояние между обкладками которого d, вдвигаются пластинки из одного итого же диэлектрика с относительной проницаемостью ε, но разных толщин. Конденсатор соединен с источником напряжения, который создает на его обкладках разность потенциалов U. а) как изменится емкость конденсатора в зависимости от толщины вдвигаемой пластинки? б) Найти зависимость от толщины пластинки Е1 и Е2 – напряженности электрического поля в диэлектрике и воздушной прослойке соответственно. Проводящая сфера радиуса R находится внутри концентрического с ним диэлектрического шара радиуса r с относительной проницаемостью ε. Определить емкость проводящей сферы. Вычислить энергию заряженного уединенного шара радиуса R в однородной среде с проницаемостью ε. Заряд шара q. Вычислить энергию двух заряженных металлических шаров, находящихся на большом расстоянии друг от друга. Радиусы шаров а и b, заряды q1 и q2. Расстояние между центрами шаров r (r>>a,b). Вычислить энергию равномерно заряженного по объему шара, находящегося в вакууме. Диэлектрическая проницаемость шара ε. Заряд шара q. Определить поле, создаваемое заряженным проводящим шаром радиуса а и зарядом q. Диэлектрическая проницаемость окружающей среды ε=ε(r), где r – расстояние от центра шара. Определить поверхностную плотность на связанных зарядов на границе диэлектрика и шара. Вычислить емкость цилиндрического конденсатора с длиной L и радиусами обкладок R1 и R2. Между обкладками конденсатора два коаксиальных слоя однородных диэлектриков с проницаемостью ε1 и ε2, граница раздела между ними – цилиндрическая поверхность радиуса R0. |
