Управления предприятием, система электронного документооборота
 Скачать 184.59 Kb. Скачать 184.59 Kb.
|
В настоящее время во всех компаниях связи внедряется и эксплуатируется широкий набор корпоративных информационных систем. Например, ERP-система управления предприятием, система электронного документооборота, CRM - система управления взаимоотношениями с клиентами и другие, которые определенным образом взаимодействуют между собой. Поэтому, с постоянным ростом автоматизации и совершенствовании бизнес-процессов, актуальными являются задачи анализа работы и оптимизации систем. В данной статье для описания совокупности взаимосвязанных информационных систем, исследования их характеристик и способа оптимизации предлагается использовать тензорный метод анализа систем, который позволяет представить любую систему в виде удобного для анализа набора величин. В теории Г. Крона основополагающими являются два постулата, смысл которых заключается в следующем: во-первых, объединение элементов не вносит никаких новых физических явлений, не наблюдаемых в примитивном элементе, а уравнение, описывающее поведение сложной системы, записывается аналогично уравнению состояния примитивного элемента, но в матричном виде; во-вторых, при изменении структуры сложной системы изменяются только элементы матричного уравнения, а переход к описанию новой структуры осуществляется с помощью матрицы перехода C [1].
Технология применения тензорного метода для моделирования, расчета, анализа, прогнозирования и управления сложными системами включает в себя следующие основные этапы: · Установление и анализ аналогий между предметной областью и сетью, включая анализ необходимой для моделирования размерности элементов сети · Определение источников информации и формирование баз данных, которые способны описать поведение исследуемой системы в терминах измеримых величин · Приведение уравнений поведения исследуемой системы к тензорному виду по отношению к изменению ее структуры · Построение сетевой модели, т.е. установление соответствия между величинами и структурой исследуемой системы и параметрами и структурой сети · Расчет сетевой модели и анализ полученных результатов для различных вариантов изменения воздействий и вариантов структуры связей · Применение полученных результатов к исследуемой системе для анализа ее состояния, прогнозирования поведения, выработки управляющих воздействий · Формирование заданных критериев, которые должна обеспечивать система и применение сетевой модели для синтеза вариантов структуры, обеспечивающих выполнение этих критериев. Основой моделирования сложных систем являются аналогии и подобие величин, уравнений процессов, структурных связей, так как это позволяет по частному делать выводы о целом по законам преобразования. Тензорный анализ ВВХ информационно-коммуникационных систем основан на следующих предположениях. 1. Поток вызовов с одной и той же интенсивностью ( λ ) поступления определяет при неизменной интенсивности обслуживания одинаковую загрузку (ρ) устройств при изменении структуры сети; таким образом, можно считать, что будет выполняться соотношение (инвариант) [6, 7]: ρλ=ρ′λ′ , (1) где переменные ρλ соответствуют одной (исходной) структуре сети, а ρ′λ′ — другой (примитивной). 2. Объединение систем в единую сеть не вызывает никаких изменений процесса обслуживания информационного потока, т.е. анализ любой сложной системы (сети) связан с определением простейшего элемента, его свойств и переносом алгоритма анализа на сложную систему (сеть) в целом. 3. Изменение структуры сети не предполагает качественного изменения основных соотношений между физическими величинами, описывающими простейший элемент, а определяет только их численное изменение [2]. Исходя из уравнения (1) и применяя соотношение между интенсивностями исходной и примитивной сетей: λ= λ′C , можно записать: ρ′Cλ = ρλ, где С — матрица перехода. Далее, находим соотношение между загрузками примитивной и исходной сетей как ρ = CTρ′ или ρ′ = 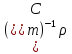 . Следовательно, подставив полученное соотношение в выражение ρ=λT , получим . Следовательно, подставив полученное соотношение в выражение ρ=λT , получим 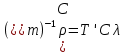 . Таким образом, можно записать . Таким образом, можно записать 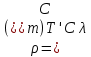 и окончательно и окончательно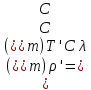 . (2) . (2)Далее, решая полученное уравнение относительно λ, находим коэффициенты использования определенной системы в исходной сети. Исходя из решения уравнения (2), можно найти как вероятность потерь заявок на обслуживание и время их задержки, так и оценить пропускную способность сети в целом. 3. Рассмотрим конкретный пример. Возьмем, например, процесс работы с отчетностью в компании Ростелеком. Изначально, заявки поступают от всевозможных отделов (заказчиков), которые попадают руководителям направления по созданию выгрузок и отчетов в системе. Далее, идет распределение ответственным за реализацию – разработчикам. Они после отработки поступившей задачи направляют ее напрямую к заказчику (заявителю). Модель исследуемой сети имеет структуру, которая представлена на рис. 1. Рисунок 1 – Исследуемая сеть массового обслуживания Геометрические объекты, необходимые для описания исходной сети, и уравнения состояния исходной сети, выраженные в матричной форме, имеют тот же вид, что и для примитивной (вспомогательной) сети, отличаясь лишь значениями компонент. Геометрические объекты, описывающие примитивную сеть, представлены на рисунке 2. 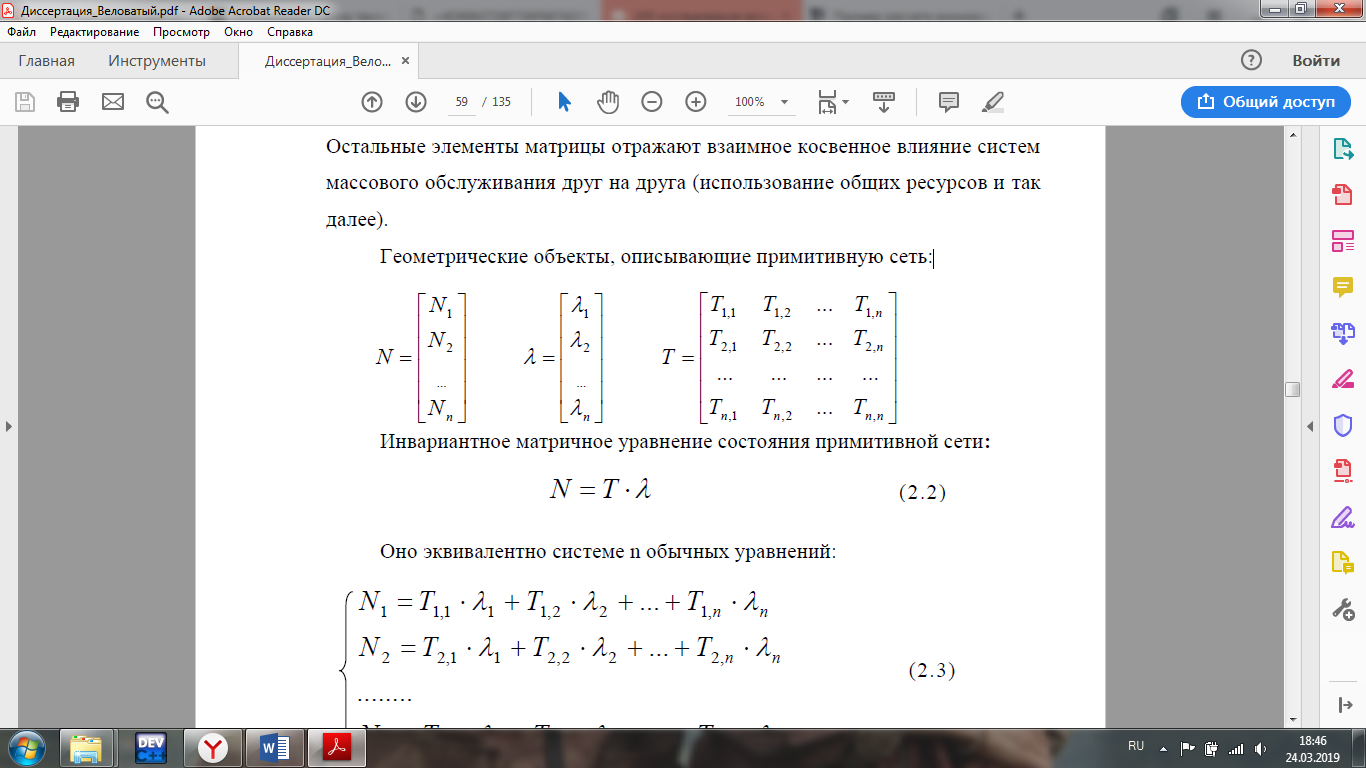 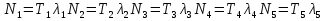 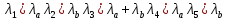 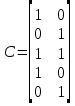 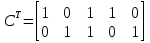 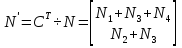 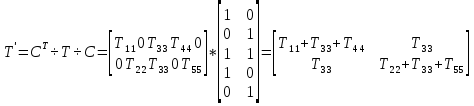 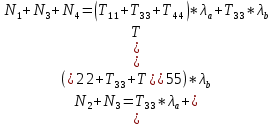 Литература
Иродова Мария Сергеевна Магистрант I курса Сибирского государственного университета телекоммуникация и информатики, г. Новосибирск, e-mail: masha.irodova@yandex.ru. |
