Открытый урок. Упрощение выражений
 Скачать 89.61 Kb. Скачать 89.61 Kb.
|
Урок по математике в 6-м классеТЕМА: "Упрощение выражений "Чайдонов Владимир Александрович, учитель математики Урок математики 6 класс Тип урока: Применение знаний, умений, навыков Оборудование: проектор, компьютер, сигнальные карточки, оценочный лист, карточки-подсказки для рефлексии, тесты. Технологии: личностно – ориентированная, информационно – коммуникационная. Формы работы: индивидуальная, парная, групповая. Цель урока: закрепить навыки и умения обучающихся в упрощении выражений, учить применять полученные знания на практике. Задачи: Общеобразовательные: совершенствовать вычислительные навыки учащихся; продолжить работу по формированию навыков решения текстовых задач и уравнений. Способствовать выработке навыков и умений при приведении подобных слагаемых, упрощении выражений. Развивающие: развитие памяти учащихся, логического мышления; развитие познавательного интереса к математике; развитие умений организации учебного труда; Воспитательные: воспитывать умение работать в группе и в паре; умение слушать другого и уважать чужое мнение; чувство толерантности; учить взаимовыручке, взаимоуважению, взаимопомощи при работе в группе Планируемые результаты: познавательные УУД: самостоятельное выделение и формулирование познавательной цели, осознанное и произвольное построение речевого высказывания в устной форме, выбор наиболее эффективных способов решения задач, структурирование знаний; личностные УУД: установление обучающимися связи между целью учебной деятельности и ее мотивом, самоопределение; регулятивные УУД: целеполагание, планирование, оценка результатов работы, внесение необходимых дополнений и коррективов в план и способ действия в случае расхождения эталона, реального действия и его результата; коммуникативные УУД: планирование учебного сотрудничества с учителем и сверстниками, соблюдение правил речевого поведения, умение высказывать и обосновывать свою точку зрения. ХОД УРОКА I. Организационный момент (1 мин.). - Здравствуйте ребята! Наш сегодняшний урок я хотел бы начать со следующих слов: «Учение математике – это искусство, это творение красоты, повседневная встреча с прекрасным, победа человеческого разума над загадками природы и мира». - Математика помогает тем, кто её умеет её применять. А умеет применять обычно кто? Кто хорошо её знает. - Что нам надо для того, чтобы тоже хорошо знать математику? • Желание учиться, знать новое. • Внимание. • Наблюдательность. • Прилежание. • Уверенность в себе. • Организованность и т.д. - Над формированием многих из этих качеств мы работаем на каждом уроке, продолжим эту работу и сегодня. - Оценивание ваших знаний вы будете вести с помощью «Оценочного листа» в форме самооценки, а в завершении урока каждый ученик, в соответствии с набранным количеством баллов, получает соответствующую отметку. (Оценочный лист получает каждый ученик перед началом урока). - Своё настроение на начало урока давайте продемонстрируем с помощью вложенных в конверт смайликов. Дерево настроений (Учащиеся открывают конверт, извлекают из него три карточки и поднимают одну, соответствующую их психологическому настроению) 2. Рефлексия (на начало урока): Выбери из предложенных рисунков тот, который соответствует твоему настроению на начало урока и отметь его. Проверка организации рабочего места: - наличие учебника, рабочей тетради, дневника учащегося, «оценочного листа», письменных принадлежностей, сигнальных карточек.- Есть ли вопросы по домашней работе … - Сегодня мы изучаем новую тему «Упрощение выражений». II. Повторение пройденного материала (8 мин.). - Давайте определимся с целями урока. (Слайд №2). – Урок начнем с того, что вспомним переместительный, сочетательный и распределительные законы математики (Слайд №3). Слайд №4 Переместительные законы a + b = b + a Сумма двух чисел не изменяется при перестановке слагаемых. a · b = b · a Произведение двух чисел не изменяется при перестановке множителей. Слайд №5 Пример 0,3 · (-2) = -2 · 0,3 = -0,6 5 + 1,2 = 1,2 + 5 = 6,2 Слайд №6 Сочетательные законы (a + b) + c = a + (b + c) Чтобы прибавить к сумме двух чисел еще одно число, можно сначала сложить его со вторым слагаемым, а потом к полученной сумме прибавить первое слагаемое. a · (b · c) = (a · b) · c Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель. Слайд №7 Пример (75 + 18) + 25 = (75 + 25) + 18= 100 + 18 = 118 (0,4 · 0,1) · 25 = (0,4 · 25) · 0,1 = 10 · 0,1 = 1 Слайд №8 Распределительные законы математики (a + b) · c = ac + bc Для того, чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. (a - b) · c = ac – bc Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе. Слайд №9 Пример: (75 + 18) · 2 = 75 · 2 + 18 · 2 = 150 + 36 = 186 (0,4 – 0,1) · 25 = 0,4 · 25 – 0,1 · 25 = = 10 – 2,5 = 7,5 III. Изучение нового материала (8 мин.). Слайд №10. - Математическое выражение – это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления и скобок. Слайд №11.  Слайд №12. - Рассмотрим выражение 3х – 8х = –5х Слагаемые 3х и -8х отличаются коэффициентами. Такие слагаемые называются подобными. Кроме того, подобными считают и равные слагаемые (3х и 3х), а также числа (5, 3, -8 и т.д.) Слагаемые, у которых равны коэффициенты, а буквенные множители различны, подобными не являются (7х и 7у)  Слайд №13. - Решим № 546. Проверим: а) –3х + х = –2х; б) 2а + 5 – 7а = 5 – 5а; в) 8 – с + 15с = 8 + 14с; г) 18 + т – 4т = 18 – 3т. Упрощая данные выражения, мы находим алгебраическую сумму подобных слагаемых. Такое действие называют приведением подобных слагаемых. IV. Закрепление нового материала (10 мин.). Слайд №14. № 548 (б; г); № 550 (б; г); № 553 (б; г); № 570 (б; г; е). № 548 (б, г) б) -0,28х + 2,7х – 3,401х = (-0,28 – 3,401) х + 2,7х = -3,681х + 2,7х = -0,981х; г) -6,3х + 2,8х – 19,2х = (-6,3 – 19,2) х + 2,8х = -25,5х + 2,8х = -22,7х. № 550 (б, г) б) 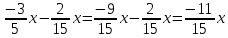 ; ;г) 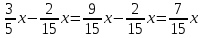 . .№ 553 (б; г) б) 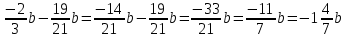 ; ;г) 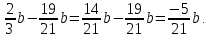 № 570 (б; г; е) б) 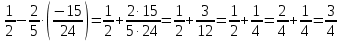 ; ;г) 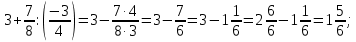 е) 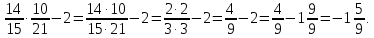 V. Самостоятельная работа (10 мин.). Слайд №15. Выполните тест на компьютере: в столбце «ОТВЕТ» поставить цифру соответствующую цифре правильного ответа из столбца «ЦИФРЫ ОТВЕТОВ»
(количество правильно выполненных заданий подсчитывается автоматически и оценку выставляет компьютер). VI. Итог урока (4 мин.). Слайд №16. Какие слагаемые называются подобными? Слагаемые, у которых одинаковые переменные (буквы), называются подобными. На основании какого арифметического закона приводятся подобные слагаемые? Приведение подобных слагаемых. Слайд №17. Домашнее задание № 547; № 548 (а; в); № № с 549 (а; в) по 553 (а; в). VII. Выставление оценок (2 мин.). Разъяснение детям, из чего получились в итоге оценки (берется средняя арифметическая за урок и самостоятельную работу, если ученик активно участвовал (решал) в повторении пройденного и изучении нового материала или выставляется оценка только за самостоятельную работу). VIII. Рефлексия (2 мин.). - Что вам понравилось на этом уроке? - Какие моменты вы бы хотели видеть на других уроках математики? | |||||||||||||||||||||||||||||||||
