физ. уральский государственный университет путей сообщения
 Скачать 23.23 Kb. Скачать 23.23 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования «УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» ( ФГБОУ ВО УрГУПС ) Факультет управления процессами перевозок Расчетно-графическая работа №2 по дисциплине: «Математика» Функции нескольких переменных
Екатеринбург 2022 Вариант 8 2. Найти частные производные первого порядка функции z =2 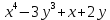 ( в аналитическом виде), производную функции в точке M(2,1) в направлении, идущем от этой точки к точке N(5,3), градиент в точке M ( в аналитическом виде), производную функции в точке M(2,1) в направлении, идущем от этой точки к точке N(5,3), градиент в точке M1. 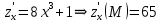 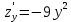 +2 +2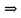 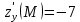 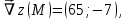 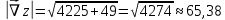 2. 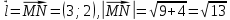 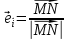 = =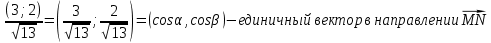 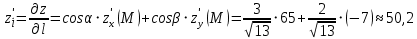 + +3. Сравним значения модуля градиента и частной производной по направлению MN. Так как модуль градиента – частная производная в направлении наибольшего возрастания, ожидается, что модуль градиента не меньше, чем абсолютное значение любой частной производной: Так как 50,2  65,38 и ожидаемое соотношение 65,38 и ожидаемое соотношение 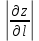 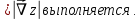 Ответ: выделенные элементы в решении.+ 5. Вычислить значение функции z=3-4 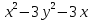 при х=2 и у=1. Построить уравнения касательной плоскости и нормали к поверхности, задаваемой функцией двух переменных z=z(x,y), в точке (2;1; z(2,1)). при х=2 и у=1. Построить уравнения касательной плоскости и нормали к поверхности, задаваемой функцией двух переменных z=z(x,y), в точке (2;1; z(2,1)). 1) Вычислим значение функции при х=2 и у=1: z(2;1) = 3-16-3-3*2= -22 2)Найдём частные производные в точке: 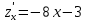 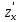 (2;1) = -16-3= -19 (2;1) = -16-3= -19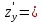 -6y -6y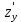 (2;1) = -6 (2;1) = -6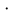 1= -6 1= -63) Тогда уравнение касательной плоскости к поверхности в точке: 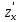 (2;1)(x- (2;1)(x-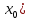 + +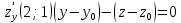 -22(x-2)-6(y-1) - (z+22)=0 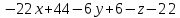 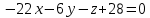 4) Уравнение нормали запишем в виде: 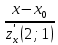 = = 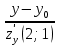 = =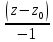 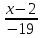 = = 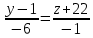 6. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции z = 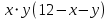 . . 1. Найдем стационарные точки. Для этого предварительно найдем выражения для частных производных заданной функции: 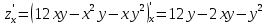 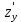 = =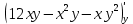 = =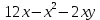 Составим и решим систему уравнений 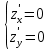 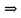 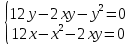 Вынесем за скобку: 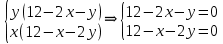 Тогда 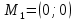 , , Рассмотрим случай, если 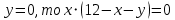 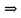 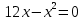 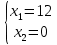 , Тогда , Тогда 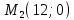 Рассмотрим случай, если х=0, то 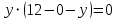 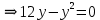 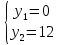 , Тогда , Тогда 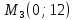 Вернемся к системе уравнений из двух неизвестных. Из 1 уравнение выразим y, тогда получим: 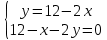 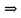 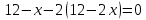 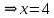 Подставим х в 1 уравнение 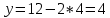 Тогда 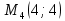 Проверим выполнение достаточного условия экстремума в каждой стационарной точке. 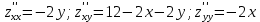 Определяем значение частных производных второго порядка в каждой стационарной точке. 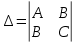 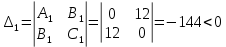 , Определитель меньше 0, точка не является экстремумом , Определитель меньше 0, точка не является экстремумом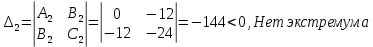 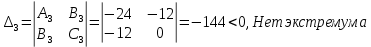 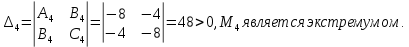 т.к 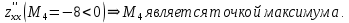 Таким образом, точка с координатами 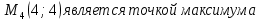 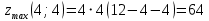 Ответ: 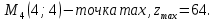 | ||||
