20-40-БПЗ-4,5-1д Еремина (Евдокимова) Светлана Сергеевна. Уравнение парной регрессии и определение их параметров
 Скачать 118.86 Kb. Скачать 118.86 Kb.
|
 Московский психолого-социальный университет Факультет психологии Контрольная работа на тему: «Уравнение парной регрессии и определение их параметров» Вариант № 5 Исполнитель: Студентка 2 курса заочной формы обучения 20-40-БПЗ-4,5-1д Еремина (Евдокимова) Светлана Сергеевна Работу проверил: Доцент, канд. экон. наук Судариков Г.В. Черняховск, 2022 г. Эконометрические модели Одной из главных задач в эконометрии в рыночной экономике является тщательное изучение количественных связей между показателями для лучшего понимания хозяйственных явлений и процессов, что в свою очередь позволяет более обоснованно сформулировать эконометрические и управленческие решения, дать прогнозы на будущее. Для решения этой или других задач необходимо построить экономические модели. Модель, которая описывает связь между экономическими показателями, называется общей, если она действует для всей генеральной совокупности наблюдений. В линейной эконометрической модели имеет место линейная связь между переменными, которые характеризуют рассматриваемый эконометрический процесс или явления. Линейные эконометрические модели наиболее просты и, в подавляющем большинстве, достаточны для практики. Те из моделей, которые базируются на методе наименьших квадратов (МНК) при оценивании их параметров, называются классическими. Изучаются в классической эконометрии, и основывается в основном на корреляционно-регрессивном анализе. При нарушении условий исполнения МНК приходится применять другие методы оценивания параметров эконометрических моделей. В общем матричном виде эконометрическая модель для фактических данных записывается так: 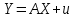 где A – матрица параметров модели размером 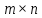 (где m-количество независимых параметров, n-число наблюдений); (где m-количество независимых параметров, n-число наблюдений);Y – матрица значений зависимой переменной; X – матрица независимых переменных; u – матрица случайных составляющих. Виды уравнений парной регрессии и определение их параметров. В регрессионном анализе одной из центральных мест имеет место ввиду своей простоты, уравнение парной регрессии. Здесь связь зависимой переменной осуществляется с одним видом независимых переменных (Х). Наиболее часто в экономике и управлении исполняются такие виды уравнений парной регрессии: a) Линейная зависимость - 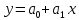 (1); (1);б) Параболическая зависимость - 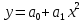 (2); (2);в) Гиперболическая зависимость - 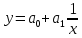 (3); (3);г) Степенная зависимость - 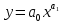 (4) и другие. (4) и другие.Уравнения со 2 по 4 являются не линейными, но соответствующими преобразованиями их можно свести к линейному типу.    y a  б бx а – прямая зависимость. б – обратная зависимость.    y   параболическая зависимость.    гиперболическая зависимость.    у  x xстепенная зависимость. Использование МНК для оценки теоретических параметров модели, рассмотренных видов уравнений парной регрессии, приводит к таким системам нормальных алгебраических уравнений. Линейная зависимость: 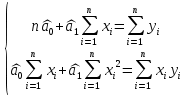 Параболическая зависимость: 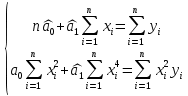 Гиперболическая зависимость: 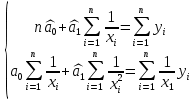 Степенная зависимость: 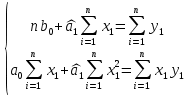 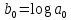 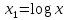 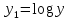 Решение приведенных систем нормальных уравнений парной регрессии позволит найти оценки параметров модели. Вариант 5. Оценить параметры экономической модели, которая характеризует зависимость между розничным товарооборотом и доходами населения. Исходные данные выборочного наблюдения за неделю для десяти семей в условных единицах приведены в таблице 1. Таблица 1 Исходные данные.
Решение Вначале по фактическим данным в таблице устанавливаем принадлежность переменных к группам не зависимых и зависимых: очевидно, что за независимую переменную 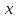 принимаются доходы населения, а за зависимую (результирующую) принимаются доходы населения, а за зависимую (результирующую) 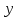 – розничный товарооборот. Для спецификации эконометрической модели необходимо выбрать одну из аналитических зависимостей. Такой выбор осуществляется или на основании опыта построения аналогичных моделей, или (при его отсутствии) путем графического изображения зависимости фактических переменных и подбора за ним одной из аналитических формул. – розничный товарооборот. Для спецификации эконометрической модели необходимо выбрать одну из аналитических зависимостей. Такой выбор осуществляется или на основании опыта построения аналогичных моделей, или (при его отсутствии) путем графического изображения зависимости фактических переменных и подбора за ним одной из аналитических формул.Как видно из рисунка 1, размещение точек лучшего всего отличает линейные зависимости для парной регрессии. 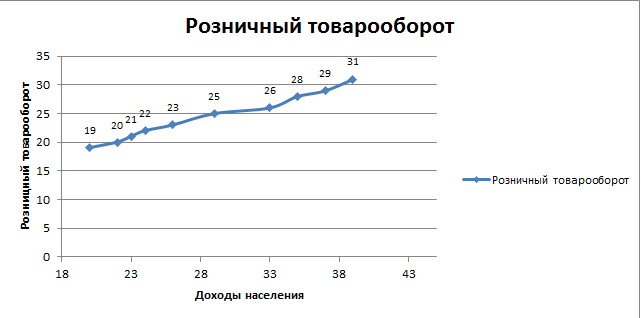 Рис. 1 Тогда экономическая модель специфицируется в такой линейной формуле: 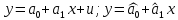 где где 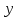 – розничное значение товарооборота; – розничное значение товарооборота;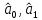 – оценки параметров модели; – оценки параметров модели;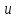 – случайная составляющая (остатки). – случайная составляющая (остатки).Как видно из рисунка 1 размещение точки лучше всего отличает линейное уравнение зависимости для парной регрессии. Тогда эконометрическая модель специфицируется в такой линейной формуле: y = 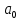 + + 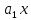 + u + uy = 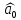 + + 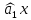 , ,где y – розничное значение товарооборота 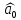 , , 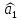 – оценки параметров модели – оценки параметров моделиu – случайная составляющая (остатки) Оценим параметры теоретической модели y = 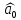 + + 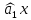 . С помощью метода наименьших квадратов. . С помощью метода наименьших квадратов.Для этого запишем систему нормальных уравнений парной регрессии для данной задачи: 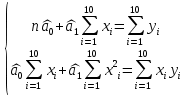 Вычисление сумм приведено в промежуточной расчетной таблице 2. Таблица 2 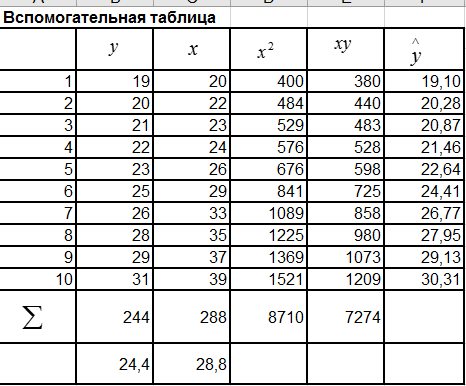  Решение системы уравнений дает такие значений оценок параметра: 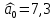 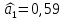 Уравнение регрессии будет иметь вид y = 7,30 + 0,59x. Уравнение регрессии (расчетные значения) представлено на рисунке 2. 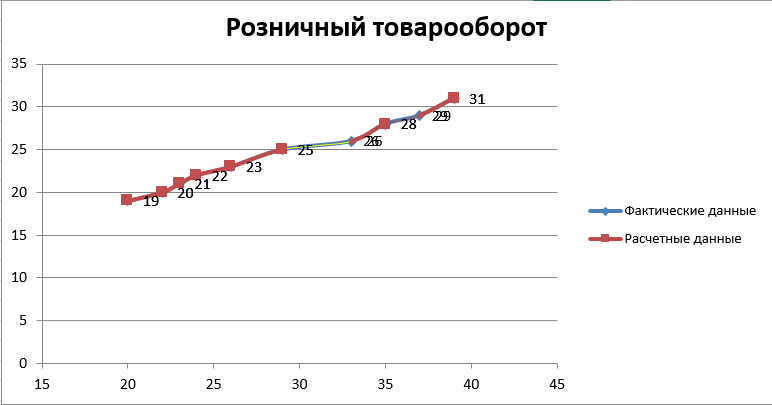 Рисунок 2 Это уравнение количественно оценивает связь недельного розничного товарооборота и доходов населения. Сделаем теоретические выводы. Параметр 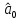 =7,30 (экономического смысла не имеет) =7,30 (экономического смысла не имеет)Параметр 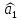 = =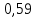 (характеризует ограниченный размер расходов на покупку товаров в розничной торговле). (характеризует ограниченный размер расходов на покупку товаров в розничной торговле).То есть, когда доход увеличится на единицу, то объем розничного товара возрастает на 0,59. По полученным данным можно определить также коэффициент эластичности (относительный эффект влияния фактора Х на результат Y) розничного товарооборота в зависимости от доходов населения. 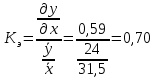 где 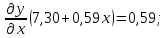 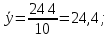 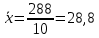 Коэффициент эластичности показывает, на сколько процентов в среднем изменится результат Y с изменением фактора X на 1%. Вывод. На основании коэффициента эластичности можно сделать вывод, что с увеличением доходов населения на 1% розничный товарооборот растет на 0,70%. |
