Урок 1 цифры
 Скачать 321.69 Kb.
|
|
Урок 1 цифры Цели: формировать умение выполнять кратное сравнение между разрядными единицами; вычислять значение числового выражения, связанного с порядком действий со скобками; периметр и площадь прямоугольника; сравнивать значения двух выражений. Ход урока I. Устный счет. 1. Разгадайте правило и вставьте числа в пустые «окошки»: 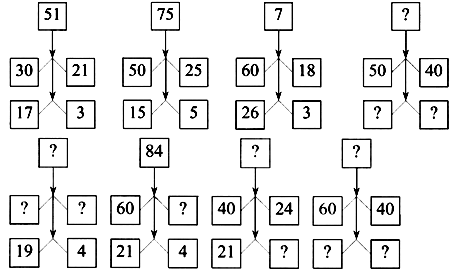 2. Назовите все многоугольники, изображённые на чертеже. 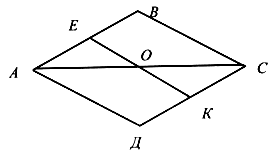 II. Работа по учебнику. Задание 1. Какие числа называются шестизначными? Назовите разряды шестизначного числа. Запишите шестизначное число, каждая цифра записи которого совпадает с номером разряда, следующего за разрядом, в котором она находится. (765 432.) Задание 2. Запишите самое большое шестизначное число, в записи которого три раза встречается цифра 1. (987 111.) Задание 3. Составьте и запишите пары чисел, каждая из которых состоит из шестизначного числа и пятизначного числа, а результат разностного сравнения между числами в паре равен 5. Сколько таких пар получилось? (5 пар.) 100 000 – 5 = 99 995 100 003 – 5 = 99 998 100 001 – 5 = 99 996 100 004 – 5 = 99 999 100 002 – 5 = 99 999 Задание 4. Выполните краткое сравнение между разрядными единицами 100 и 10. (100 : 10 = 10.) – Составьте и запишите ещё четыре пары разрядных единиц с таким же результатом кратного сравнения. 1000 : 100 = 10 100 000 : 10 000 = 10 10 000 : 1000 = 10 1 000 000 : 100 000 = 10 Задание 5. Выполните устные вычисления: 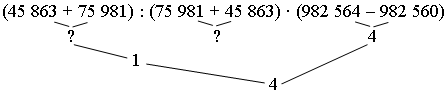 – Какие знания помогли вам выполнить это задание? Задание 6. Сравните устно значения двух выражений. Составьте из них верное равенство или неравенство. Запишите его. 983 657 – (983 657 – 144) = 144 000 : 100 · (569 873 – 569 872) – Какие знания помогли вам выполнить это задание? Задание 7. Выполните столбиком умножение.  III. Фронтальная работа. – Назовите признаки, по которым похожи все пары чисел: 390089 и 30089; 560054 и 40065; 780090 и 70098; 190004 и 90004. – Вычислите значения суммы и разности чисел в каждой паре. – Выпишите ответы в порядке убывания. – Запишите по этим же признакам другие пары чисел и ответьте на вопросы: а) На сколько одно число меньше другого? б) На сколько одно число больше другого? в) По каким признакам похожи все числа первого столбика? Второго столбика? г) Вычислите разность наибольшего и наименьшего чисел в первом столбике. д) Вычислите сумму наибольшего и наименьшего чисел во втором столбике. – Увеличьте каждое число в 2 раза. – Увеличьте каждое число в 3 раза. IV. Итог урока. – Назовите разряды и классы шестизначного числа. – Сформулируйте алгоритм уменьшения в столбик. Урок 2 Повторение изученного в 3 классе Цели: учить измерять с помощью палетки площадь прямоугольника; формировать умение чертить квадрат с данной стороной; закреплять умение методом подбора определять длину и ширину прямоугольника по известной площади; формулировать задачу по краткой записи. Ход урока I. Устный счет. – Чему равно произведение чисел 9 и 8, 7 и 6, 4 и 6? – Чему равно частное чисел 48 и 6, 54 и 9, 18 и 2? – Запишите числа 27, 81, 36, 48, 24 в виде произведения однозначных чисел. – Запишите числа 6, 7, 8, 9 в виде частного двух чисел. – Поставьте знаки арифметических действий разными способами так, чтобы выполнялся данный порядок действий: 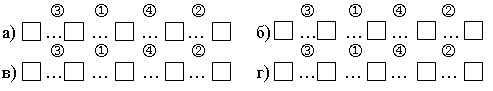 II. Работа по учебнику. Задача 8. Что известно в задаче? Какую фигуру называют прямоугольником? Как вычислить периметр прямоугольника? Длина – 5 см 5 мм = 55 мм. Ширина – 3 см = 30 мм. Р – ? S – ? Решение: 1) Р = (55 + 30) · 2 = 85 · 2 = 170 (мм). р = 170 мм = 17 см. 2) S = 55 · 30 = 1650 (мм2). 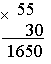 Ответ: Р = 17 см; S = 1650 мм2. Задание 9. Учащиеся чертят два прямоугольника по данным таблицы и завершают заполнение таблицы в тетради.
Решение: 1) Р1 = (4 + 3) · 2 = 14 (см). 2) S1 = 4 · 3 = 12 (кв. см). 3) Р2 = (6 + 2) · 2 = 16 (см). 4) S2 = 6 · 2 = 12 (кв. см). – Сравните периметры и площади этих прямоугольников. (Разные, равные.) Вывод: прямоугольники могут иметь разные периметры, но равные площади. Задание 10. Учащиеся чертят два прямоугольника по данным из таблицы и завершают заполнение этой таблицы.
Решение: 1) Р1 = (8 + 2) · 2 = 20 (см); 2) S1 = 8 · 2 = 16 (кв. см); 3) Р2 = (6 + 4) · 2 = 20 (см); 4) S2 = 6 · 4 = 24 (кв. см). – Сравните периметры и площади этих прямоугольников. (Равные, разные.) Вывод: прямоугольники могут иметь равные периметры, но разные площади. З  адание 11. Какую фигуру называют квадратом? Периметр квадрата равен 32 дм. На сколько квадратных дециметров увеличится площадь квадрата, если его периметр увеличить на 12 дм?Решение: 1) 32 : 4 = 8 (дм) – сторона 1-го квадрата; 2) 8 · 8 = 64 (кв. дм) – площадь 1-го квадрата; 3) 32 + 12 = 44 (дм) – периметр 2-го квадрата; 4) 44 : 4 = 11 (дм) – сторона 2-го квадрата; 5) 11 · 11 = 121 (кв. дм) – площадь 2-го квадрата; 6) 121 – 64 = 57 (кв. дм) – больше площади 2-го квадрата. Задание 12. Учащиеся с помощью палетки измеряют площадь данного прямоугольника. (15 кв. см.) Задание 13. На сколько минутных делений должна повернуться минутная стрелка, чтобы получился поворот на прямой угол? (На 15 минут.) –  Какую часть прямого угла составляет угол, на который поворачивается минутная стрелка за 5 минут? (Третью часть.)Задание 14. Учащиеся выполняют построение. Задание 15. Какими могут быть длина и ширина прямоугольника, если его площадь равна 20 кв. см?
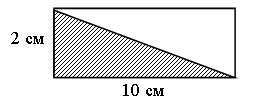–  Постройте треугольник с площадью 10 кв. см.III. Итог урока. – Как вычислить периметр прямоугольника? – Как вычислить площадь прямоугольника? Урок 3 Повторение изученного в 3 классе Цели: учить формулировать задачу по данному решению; закреплять умение формулировать задачу по данной диаграмме; формировать умение решать арифметические задачи; формулировать задачи на разностное сравнение, в условии которой одно из данных является результатом кратного сравнения; развивать умение анализировать и обобщать. Ход урока I. Устный счет. 1. Обозначьте порядок выполнения действий на каждой схеме и объясните, каким правилом порядка выполнения действий в выражениях вы пользовались: 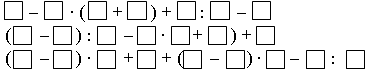 2. Задача. Масса трех одинаковых коробок пряников равна 18 кг. Коробка зефира на 2 кг легче коробки пряников. Чему равна масса 6 коробок зефира? – Выберите выражение, которое является решением данной задачи: а) 18 : 3 – 2 · 6; б) (18 : 3 – 2) · 6. 3. Догадайтесь, какая фигура «лишняя». 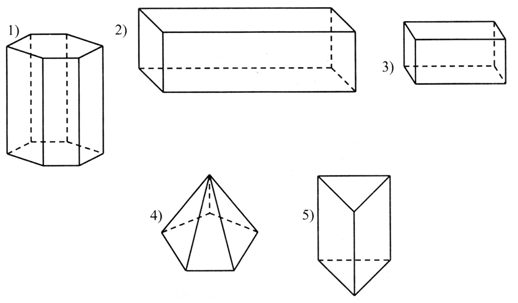 II. Работа по учебнику. Задание 16. Рассмотрите краткую запись задачи. Сформулируйте задачу по краткой записи. Выполните решение. Решение: 1) 14 – 3 = 11 (лет) – Ире; 2) 11 – 1 = 10 (лет) – Марине. Ответ: 10 лет. Задание 17. Прочитайте задачу. Что известно? Что требуется узнать? Выполните краткую запись и решите задачу. 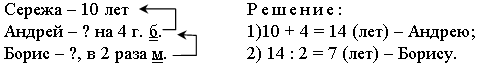 Ответ: 7 лет. Задание 18. Учащиеся составляют задачу по данному выражению 12 · 10 + 15 · 8. 1-й день – 10 ящ. по 12 кг; 2-й день – 8 ящ. по 15 кг. Всего – ? Решение: 1) 12 · 10 = 120 (кг) – продали в 1-й день; 2) 15 · 8 = 120 (кг) – продали во 2-й день; 3) 120 + 120 = 240 (кг) – всего. Ответ: 240 кг. Задание 19. Учащиеся составляют задачу на кратное сравнение по диаграмме.  Решение: 90 : 15 = 6 (раз) – больше картофеля. Ответ: в 6 раз больше. Задание 20. Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. Найдите рациональный путь решения этой задачи.  Решение: I способ. 1) 18 + 3 = 21 (уп.) – увезли апельсинового сока; 2) 40 – 18 = 22 (уп.) – осталось яблочного сока; 3) 35 – 21 = 14 (уп.) – осталось апельсинового сока; 4) 22 – 14 = 8 (уп.) – больше упаковок с яблочным соком. II способ: 1) 40 – 35 = 5 (уп.) – больше было яблочного сока; 2) 5 + 3 = 8 (уп.) – больше осталось яблочного сока. Ответ: на 8 уп. больше. Задание 21. Сформулируйте задачу на разностное сравнение, в условии которой одно из данных является результатом кратного сравнения.  Решение:1) 10 · 2 = 20 (кг) – груш; 2) 20 – 10 = 10 (кг) – больше груш. Ответ: на 10 кг больше. Задание 22. Сформулируйте задачу на кратное сравнение, в условии которой одно из данных является результатом разностного сравнения.  Решение:1) 10 + 30 = 40 (кг) – груш; 2) 40 : 10 = 4 (раза) – больше груш. Ответ: в 4 раза больше. III. Итог урока. – Что нового узнали на уроке? Урок 4 Когда известен результат разностного сравнения Цели: учить решать задачи на разностное сравнение; формировать умение записывать с помощью математических выражений действия; выбирать верный вариант решения задачи. Ход урока I. Устный счет. 1. Какое число пропущено? 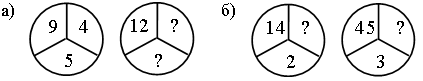 2. Решите з а д а ч у. В художественной школе занимается 90 человек. 43 человека занимаются живописью, 29 – лепкой, а остальные – резьбой по дереву. Сколько человек занимается резьбой по дереву? 3. Игра «Три стрелка». Три стрелка стреляли одинаковое число раз и набрали очков поровну. Все выстрелы попали в мишень. Кто куда попал? 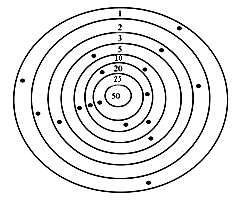 II. Сообщение темы урока. – Сформулируйте задачу по краткой записи.  – Как называются такие задачи? – Сегодня на уроке будем решать задачи, когда известен результат разностного сравнения. III. Работа по учебнику. Задание 23. Прочитайте задачу. Что известно? Рассмотрите рисунок в учебнике. Вычислите удвоенную длину меньшей части полоски. 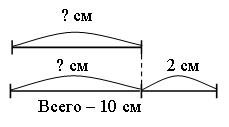 10 – 2 = 8 (см) – удвоенная длина меньшей части полоски. – Вычислите с помощью деления длину меньшей части полоски. 8 : 2 = 4 (см) – длина меньшей части полоски. – Как можно вычислить длину большей части полоски? – Выполните вычисления двумя способами. 10 – 4 = 6 (см). 4 + 2 = 6 (см). Задание 24. Учащиеся выполняют запись: 1 м = 100 см. 100 – 20 = 80 (см) – удвоенная длина меньшей части ленточки. 80 : 2 = 40 (см) – длина меньшей части ленточки. 40 + 20 = 60 (см) – длина большей части ленточки. – На сколько сантиметров одна часть ленточки длиннее, чем другая? (На 20 см.) Задание 25. Прочитайте задачу. Какой из следующих вариантов является решением данной задачи? (Второй вариант.) – Перепишите это решение с вычислением ответа в тетрадь. Задание 26. Прочитайте задачу. Что известно? Что требуется узнать? Выполните чертежи и решите задачу. Всего – 52 уч. 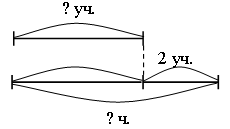 Решение: 1) 52 – 2 = 50 (уч.) – удвоенное число в меньшем; 2) 50 : 2 = 25 (уч.) – число в меньшем классе; 3) 25 + 2 = 27 (уч.) – число в большем классе. Ответ: 25 учеников; 27 учеников. Задание 27. По данной краткой записи сформулируйте задачу. Выполните ее решение. Всего – 47 чел. 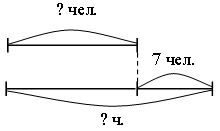 Решение: 1) 47 – 7 = 40 (чел.) – удвоенное число в 1-й бригаде; 2) 40 : 2 = 20 (чел.) – в 1-й бригаде; 3) 47 – 20 = 27 (чел.) – во 2-й бригаде. Ответ: 20 человек; 27 человек. Задание 28. Выполните вычисления. 550 – 70 = 480 480 : 2 = 240 240 + 70 = 310 Ответ: 550 = 240 + 310. Задание 29. Выполните вычисления. 235 – 135 = 100 100 : 2 = 50 135 + 50 = 185 Ответ: 185 + 50 = 235; 185 – 50 = 135. Задание 30. Учащиеся работают в парах. Сформулируйте задачу, в которой требуется найти два числа, если известно значение суммы и значение разности этих чисел.  499 – 299 = 200 399 + 100 = 499 200 : 2 = 100 399 – 100 = 299 299 + 100 = 399 Задание 31. Прочитайте задачу. Что известно? Что требуется узнать? Выполните чертеж и решите задачу. 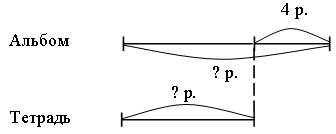 Всего – 52 р. 3 альбома – ? р. 10 тетрадей – ? р. Решение: 1) 52 – 4 = 48 (р.) – удвоенная сумма цены тетрадей; 2) 48 : 2 = 24 (р.) – цена тетради; 3) 24 + 4 = 28 (р.) – цена альбома; 4) 24 · 10 = 240 (р.) – стоимость 10 тетрадей; 5) 28 · 3 = 84 (р.) – стоимость 3 альбомов. Ответ: 240 р., 84 р. Задание 32. Прочитайте задачу. Проанализируйте начало решения задачи. Сформулируйте требование задачи. (Какова масса одного лукошка?) – Сколько граммов малины собрал Миша? 900 · 3 = 2700 (г). – Сколько граммов малины собрала Маша? 900 · 2 = 1800 (г). Задание 23. Учащиеся выполняют схему.  1) 15 – 3 = 12 (см) – удвоенная длина меньшей части; 2) 12 : 2 = 6 (см) – длина меньшей части; 3) 6 + 3 = 9 (см) – длина большей части. IV. Итог урока. – Что значит «удвоенное значение»? Урок 5 Когда известен результат кратного сравнения Цели: учить формулировать задачу по краткой записи; формировать умение решать задачи на кратное сравнение. Ход урока I. Устный счет. 1. Заполните пропуски в схемах так, чтобы получились верные равенства. Найдите все возможные решения.  2  . Задача. Два ананаса весят столько же, сколько 4 яблока, а одно яблоко – столько, сколько 3 абрикоса. На одной чаше весов – два ананаса. Сколько абрикосов надо положить на вторую чашу для равновесия?3. Рассмотрите чертеж. Какие геометрические фигуры здесь изображены? Сколько треугольников на чертеже? 4 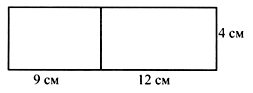 . Сколько прямоугольников вы видите на рисунке? Вычислите площадь и периметр каждого прямоугольника.II. Сообщение темы урока. – Сформулируйте задачу по краткой записи:  – Как называются такие задачи? – Сегодня на уроке будем решать задачи, когда известен результат кратного сравнения. III. Работа по учебнику. Задание 34. Рассмотрите рисунок. На сколько равных частей разрезан торт? (На 8 частей.) Какая часть торта лежит на лопатке? (1 часть.) Во сколько раз одна часть торта меньше, чем все оставшиеся части? (В 8 раз.) Сколько граммов будет в одной части, если весь торт имеет массу 800 г? (100 г.) – Запишите соответствующие вычисления. 800 : 8 = 100 (г). – Сколько граммов во всех оставшихся частях, кроме одной? (700 г.) – Запишите соответствующие вычисления. 800 – 100 = 700 (г). Задание 35. Прочитайте задачу. Рассмотрите чертеж в учебнике. Какой из данных вариантов является решением задачи? (Первый вариант.) – Выполните решение задачи. Задание 36. Прочитайте задачу. Что известно? Что требуется узнать? Выполните схему и решите задачу. 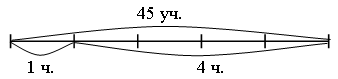 Решение: 1) 1 + 4 = 5 (ч.) – всего; 2) 45 : 5 = 9 (уч.) – в одном кружк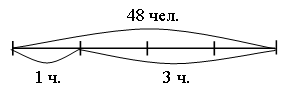е;  3) 9 · 4 = 36 (уч.) – в другом кружке.Ответ: 9 учеников, 36 учеников. Задание 37. По данной краткой записи сформулируйте задачу. Решение: 1) 1 + 3 = 4 (ч.) – всего; 2) 48 : 4 = 12 (чел.) – в 1-й бригаде; 3) 12 · 3 = 36 (чел.) – во 2-й бригаде. Ответ: 12 человек; 36 человек. Задание 38. Выполните вычисления.  Решение: 1) 1 + 9 = 10 (ч.) 2) 350 : 10 = 35 3) 35 · 9 = 315. Ответ: 315 + 35 = 350; 315 : 35 = 9 Задание 39. Учащиеся работают в парах. 140 : 20 = 7 140 + 20 = 160 Задача. Из каких двух слагаемых должна состоять сумма, чтобы одно слагаемое было больше другого в 7 раз, а ее значение равнялось числу 360? Задание 40. Найдите два числа, при сложении которых получается число 180, а при делении одного числа на другое – число 8.  Решение: 1) 1 + 8 = 9 2) 180 : 9 = 20 3) 180 – 20 = 160 Ответ: 160 + 20 = 180; 160 : 20 = 8. Задание 41. Прочитайте задачу. Что известно? Что требуется узнать? Выполните чертеж и решите задачу. 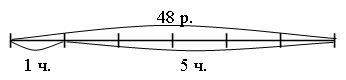 10 ручек – ? р. 3 набора фломастеров – ? р. Решение: 1) 1 + 5 = 6 (ч.) – всего; 2) 48 : 6 = 8 (р.) – цена ручки; 3) 8 · 10 = 80 (р.) – стоимость 10 ручек; 4) 8 · 5 = 40 (р.) – цена набора фломастеров; 5) 40 · 3 = 120 (р.) – стоимость 3 наборов фломастеров. Ответ: 80 р., 120 р. – На какое требование задачи можно ответить с помощью выражения 48 : (5 + 1) · 5? (Можно узнать стоимость 5 ручек.) IV. Итог урока. – Что нового узнали на уроке? – Как выполнить кратное сравнение? Урок 6 Учимся решать задачи Цели: учить составлять краткую запись задачи, заполняя таблицу; формировать умение решать задачи с опорой на схему; закреплять умение выполнять чертеж к составленной задаче; вычислять периметр прямоугольника; формулировать условие задачи по данной иллюстрации; определять площадь фигуры. Ход урока I. Устный счет. 1. Задача. Света, Лена и Зоя учатся играть на разных инструментах – флейте, арфе и баяне. Зоя и баянисты занимаются в один день, а Лена и арфистка живут в одном доме. Зоя пригласила в гости Лену и баянистку. Кто из девочек учится играть на каком инструменте? Решение:
2. Догадайтесь, по какому правилу составлены тройки чисел, вставьте число в «окошко».  3. Сравните числа: 387 ... 378 931 ... 913 504 ... 540 741 ... 714 – На сколько можно увеличить каждое число, чтобы в нем изменилась только цифра, обозначающая единицы, а цифры, обозначающие десятки и сотни, не изменялись? Запишите верные равенства. 4  . Головоломка. а) Как убрать 2 палочки, чтобы осталось 4 одинаковых квадрата? б) Как убрать 3 палочки, чтобы осталось 3 равных квадрата?  II. Работа по учебнику. Задание 42. Прочитайте задачу. Что известно? Что требуется узнать? Составьте краткую запись в виде таблицы.  Решение: 1) 85 – 7 = 78 (чел.) – удвоенное число в 1-м автобусе; 2) 78 : 2 = 39 (чел.) – в 1-м автобусе; 3) 39 + 7 = 46 (чел.) – во 2-м автобусе. Ответ: 39 человек; 46 человек. Задание 43. Найдите два числа, при сложении которых получается число 240, а при вычитании – число в 2 раза меньше, чем при сложении.  Решение: 1) 240 – 120 = 120 2) 120 : 2 = 60 3) 240 – 60 = 180 Ответ: 180 + 60 = 240; 180 – 60 = 120. Задание 44. Прочитайте задачу. Что известно? Что требуется узнать? Решите задачу. Решение: 1) 45 р. 50 к. – 5 р. 50 к. = 40 р. – удвоенная цена линейки; 2) 40 : 2 = 20 (р.) – цена линейки; 3) 20 р. + 5 р. 50 к. = 25 р. 50 к. – цена ручки; 4) 20 · 5 = 100 (р.) – стоимость 5 линеек. Ответ: 100 рублей. Задание 45. Составьте краткую запись задачи в виде таблицы.  – Выполните чертёж и решите задачу. 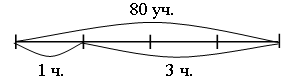 Решение: 1) 1 + 3 = 4 (ч.) – всего; 2) 80 : 4 = 20 (уч.) – в 1-й секции; 3) 20 · 3 = 60 (уч.) – во 2-й секции. Ответ: 20 учеников, 60 учеников. Задание 46. Прочитайте задачу. Что известно? Что требуется узнать? Выполните чертеж и решите задачу. 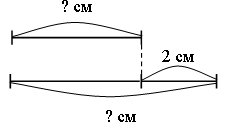 Решение: 1) 12 – 2 = 10 (см) – удвоенная длина меньшей стороны; 2) 10 : 2 = 5 (см) – длина меньшей стороны; 3) 5 + 2 = 7 (см) – длина большей стороны. Ответ: 5 см, 7 см. Задание 47. Учащиеся решают задачу, используя аналогичное решение из задания 46. Решение: 1) 24 : 2 = 12 (см) – сумма длины и ширины; 2) 12 – 2 = 10 (см) – удвоенная длина меньшей стороны; 3) 10 : 2 = 5 (см) – длина меньшей стороны; 4) 5 + 2 = 7 (см) – длина большей стороны. Ответ: 5 см, 7 см. Задание 48. Прочитайте задачу. Что известно? Что требуется узнать? Выполните чертеж и решите задачу. 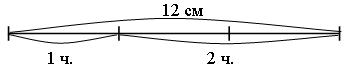 Решение: 1) 1 + 2 = 3 (ч.) – всего; 2) 12 : 3 = 4 (см) – длина меньшей стороны; 3) 4 · 2 = 8 (уч.) – длина большей стороны. Ответ: 4 см, 8 см. Задание 49. Учащиеся работают над задачей, используя решение задачи 48. Задание 50. Прочитайте задачу. Что известно? Что требуется узнать? Выполните краткую запись и решите задачу.  5 тетрадей – ? р. Решение: 1) 10 – 7 = 3 (тетр.) – стоят 75 р.; 2) 75 : 3 = 25 (р.) – цена тетради; 3) 25 · 5 = 125 (р.) – стоят 5 тетрадей. Ответ: 125 рублей. Задание 51. По данной схеме сформулируйте задачу и решите задачу. Решение: 1) 5 – 3 = 21 (меш.) – весят 50 кг; 2) 50 : 2 = 25 (кг) – весит 1 мешок; 3) 25 · 5 = 125 (кг) – весят 5 мешков; 4) 25 · 3 = 75 (кг) – весят 3 мешка. Ответ: 75 кг. Задание 52. Определите площадь каждой фигуры, если они составлены из одинаковых квадратов и площадь первой фигуры на 3 кв. см больше площади второй. Ответ: 7 кв. см; 10 кв. см. III. Итог урока. – Что нового узнали на уроке? Урок 7 Алгоритм умножения столбиком Цели: составить алгоритм умножения столбиком многозначного числа на трехзначное число; учить формулировать алгоритм умножения столбиком; формировать умение выполнять умножение столбиком многозначного числа на трехзначное; устанавливать соответствия между записями. Ход урока I. Устный счет. 1. Заполните пустые клетки магических квадратов:
2. Рассмотрите рисунок. 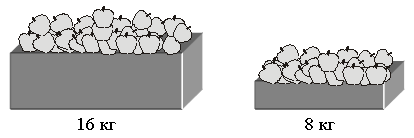 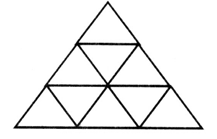 – Составьте по рисунку задачи, которые решаются так: 1) 16 + 8 3) 16 : 8 5) 8 · 2 2) 16 – 8 4) 16 · 2 6) (16 + 8) · 2 3. Рассмотрите чертеж. Сколько треугольников изображено? 4. По какому правилу составлены ряды чисел? Запишите в каждый ряд еще пять чисел по такому же правилу: 80, 160, 240, ... 60, 120, 180, ... 40, 80, 120, ... II. Работа по учебнику. Задание 53. Учащиеся выполняют умножение многозначного числа на однозначное число в столбик. 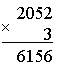 – С какого разряда первого множителя нужно начинать умножение на однозначное число столбиком и к какому разряду следует переходить далее? (Начинаем умножение с единиц, далее переходим к разряду десятков.) – А если получается двузначное число? (Пишем цифру разряда единиц.) – Какое число при умножении в данном разряде должно получиться, чтобы не было перехода через разряд? (Однозначное число.) – В каких случаях имеет место переход через разряд и как его нужно учитывать при дальнейших вычислениях? (Когда получаем двузначное число. Цифру разряда десятков запоминаем.) Задание 54. Объясните, как выполнено умножение столбиком многозначного числа на двузначное число. – На какое разрядное слагаемое второго множителя сначала умножаем первый множитель? (На единицы.) – На какое число умножаем далее? (На десятки.) – Чем отличается расположение записи результата умножения числа 2052 на 3 единицы от результата умножения этого же числа на 2 десятка? (Результат умножения на десятки начинаем писать под десятками.) – Какая цифра стоит в этом случае в разряде единиц этого результата? (Ноль.) – Обязательно ли ее записывать или можно оставить это место свободным? (Можно оставить свободным.) – Какое действие нужно выполнить над двумя полученными результатами умножения? (Сложение.) – Можно ли для выполнения этого действия применить алгоритм сложения столбиком? – Можно ли использовать уже имеющиеся записи полученных чисел или нужно делать отдельную запись? (Можно использовать.) Задание 55. Учащиеся формулируют алгоритм умножения столбиком, отвечая на вопросы. III. Самостоятельная работа. I вариант. Не выполняя умножения в «столбик», соедини каждое выражение с его значением: 4802 · 5 5268 74131 · 2 3276 364 · 9 34088 2634 · 2 24010 8522 · 4 148262 II вариант. Не выполняя умножения в «столбик», соедини каждое выражение с его значением. 2974 · 6 18921 5018 · 7 4230 7235 · 9 35126 846 · 5 17844 6307 · 3 65115 Задание 56. Учащиеся выполняют умножение. 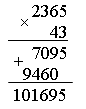 Задание 57. Учащиеся анализируют записи и устанавливают соответствие. 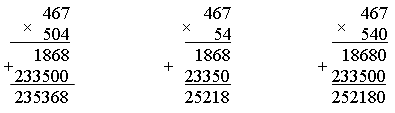 IV. Итог урока. – Сформулируйте алгоритм умножения на двузначное число столбиком. Урок 8 Поупражняемся в вычислениях столбиком Цели: учить выполнять умножение столбиком многозначного числа на трехзначное; формировать умение выполнять вычисления числового выражения со скобками. Ход урока I. Устный счет. 1. Задача. Магазин находится от дома в 150 м, а школа в 4 раза дальше от дома, чем магазин. Чему равно расстояние от дома до школы? Чему равно расстояние от магазина до школы, если оно в 2 раза больше, чем расстояние от дома до магазина?  2. Вставьте вместо пропусков одну и ту же цифру, чтобы равенство стало верным: 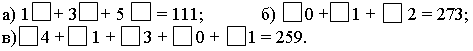 3. Ребусы. _ *3* _*4* 1*6 *3 84 392 4. Рассмотрите рисунок. 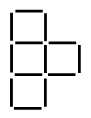 Из 13 палочек сложили 4 квадрата. Как убрать 1 палочку, чтобы осталось 3 квадрата? II. Работа по учебнику. Задание 58. Учащиеся выполняют сложение нескольких слагаемых в столбик. 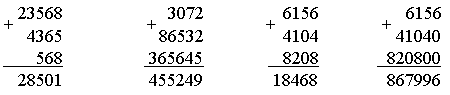 Задание 59. Проверьте, правильно ли выполнено умножение. 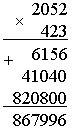 Задание 60. Учащиеся выполняют умножение столбиком. 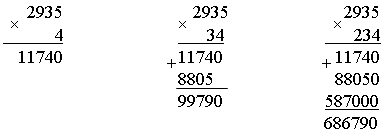 Задание 61. Найдите значения данных выражений, применив вычисления столбиком. 1 3 2 а) (3561 + 2568) · (789365 – 789331) = 208386 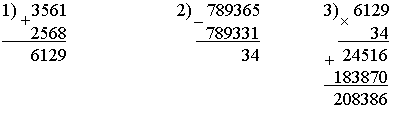 1 3 2 б) (1728 + 8327) · (87524 – 87321) = 2041165 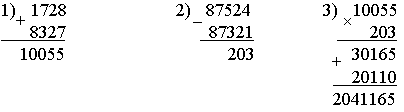 III. Работа по карточкам. Карточка 1. 1. Найдите значения разностей: 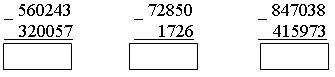 2. Найдите значения сумм. 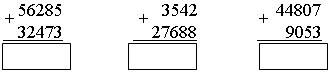 Карточка 2. 1. Найдите значения сумм.  2. Найдите значения разностей: 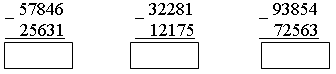 Карточка 3. 1. Найдите значения сумм.  2. Найдите значения разностей:  Карточка 4. 1. Найдите значения разностей:  2. Найдите значения сумм.  Карточка 5. 1. Найдите значения разностей:  2. Найдите значения сумм. 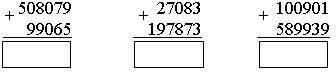 Карточка 6. 1. Найдите значения сумм. 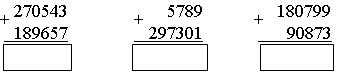 2. Найдите значения разностей: 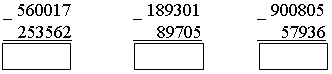 IV. Итог урока. – Что нового узнали на уроке? |