Урок №14
|
Школа: №1 Ембі қалалық ЖББОМ Утверждаю:
|
Дата: 26.09.2022
|
Ф.И.О. учителя: Жагысов Е.М.
|
Класс: 7 «р»
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Преобразование выражений, содержащих степени
|
Цели обучения, которые достигаются на данном уроке
|
7.1.2.5 применять свойства степеней для упрощения алгебраических выражений;
7.2.3.1 определять закономерности и находить недостающие члены последовательности, содержащей степени;
|
Ход урока
|
Запланированные этапы урока
|
Запланированная деятельность на уроке
|
Действия
|
Оцениание
|
Ресурсы
|
Начало урока
5 минут
|
Организационный момент
Приветствие
Создание благоприятной атмосферы
Проверка домашнего задания
|
Проверять друг друга попарно на предмет выполнения домашних заданий
|

|
психологической ситуации.
|
Середина урока
15 минут
|
Степень с целым показателем — это степень, показателем которой является любое целое число.
В прошлом уроке мы изучили степень с натуральным показателем. Этот вид степени тоже является степенью с целым показателем, поскольку натуральные числа относятся к целым числам.
Также, мы рассмотрели степень, показателем которой является 0. Этот вид степени тоже является степенью с целым показателем, поскольку 0 относится к целым числам.
Рассмотрим ещё один вид степени с целым показателем, а именно показателем которой является целое отрицательное число. Выглядят эти степени так:
2−2, 10−7, a−8
В дальнейшем любую степень с натуральным, нулевым или целым отрицательным показателем, мы будем называть степенью с целым показателем.
Вывод: частные случаи подтвердили правильность теоремы №2. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k таких, что n > k.
Доказательство теоремы 2.
Первый способ.
Воспользуемся теоремой 1. Применим ее для степеней 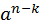 и и 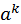 . .
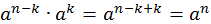
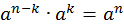 . Разделим обе части на . Разделим обе части на 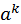 . .
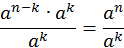

Второй способ.
Доказательство основано на определении степени
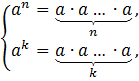
Сократим k сомножителей.

То есть  для любого а для любого а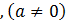 и любых натуральных n и k таких, что n > k. и любых натуральных n и k таких, что n > k.
|
"Мозговой штурм"
Один студент делает заключение по теме.
Учиники отвечают на вопрос, выполняют работу по заданному типу.
|
ИО: Оцениайте друг друга.
|
Самостоятельно осваивает новые знания
|
Работа книгой
20 минут
|
Самосттоятельная работа
«А» - №6.1, №6.4, №6.5
«В» - №7.1, №7.3
«С» - №7.8, №7.15
|
Выполнять задачи подписки в книге
|
ИО: Оценивайте друг друга звездочкой

|
Групповые задания.
|
Конец урока
5 минут
|
Домашнее задание
№6.6, №7.6
Подведение итогов
В конце урока проведем рефлексию:
|
Выполнение домашних заданий.
|
|
|
 Скачать 67.4 Kb.
Скачать 67.4 Kb.